异中求同探寻概念教学策略

【摘 要】同课异构是当前常用的一种校本教研形式。文章通过对“轴对称（一）”课例进行对比分析，从教学素材和教学方法两个角度比较“同”在何处，缘何生“异”，让教师明白同课异构不仅要同中求异，更重要的是要异中求同，以一节课的剖析，探寻这一类课的教学策略，促进教师思考和专业成长。

【关键词】同课异构;教学素材;教学方法

【作者简介】桂华，桂林市秀峰区教学研究室主任，高级教师，特级教师，主要从事小学数学教育、教师教育研究。 同课异构是近几年颇受教师欢迎的一种校本教研形式。对于同样的教学内容，不同的教师有不同的教学设计，折射出教师不同的教学理念和知识储备。目前，许多地方开展同课异构，但往往着重于“异”的比较。实则，不仅要比较其“异”，更是要异中求同，思考“同”背后的教学理念和教学规律，总结和发现这一类型学习内容的教学策略。本文以北师大版数学三年级下册“轴对称（一）”教学为例，在同课异构中探寻教学策略。

“轴对称（一）”属于图形与几何领域中“图形的运动”的内容，是一个几何概念，北师大版教材的目标定位是要让学生通过观察和操作活动，初步认识轴对称图形。学生要学会直观判断出轴对称图形，并能用对折的方法找出轴对称图形的对称轴。对于同样的教学内容，如何达成同样的教学目标，关键在于教师选取怎样的教学素材作为载体，采取什么样的教学方法引导学生开展学习。本文从教学素材和教学方法两个角度对梁丽华（下文称为教师A）和罗定玲（下文称为教师B）两位教师执教的“轴对称（一）”课例进行比较，从而寻找图形与几何领域中的概念课的教学策略。

一、紧扣概念本质，选择教学素材

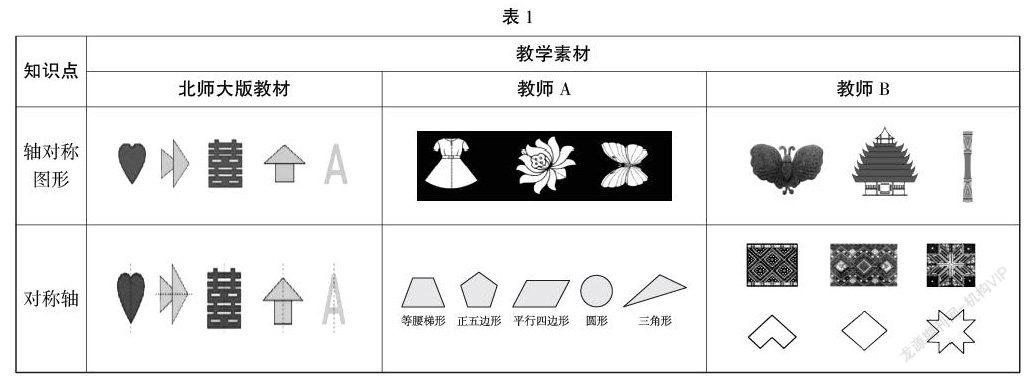
同样的教学内容，不同的教材处理方法，教学效果往往相差甚远。教师作为课堂教学的设计者和组织者，不仅体现在教学活动过程本身，还体现在如何取舍和挑选符合学生认知基础并有利于核心概念建构的教学素材上。我们对北师大版教材和这两位教师选取的教学素材进行了对比（见表1）。

教师A和教师B均未拘泥于教材。对于两个不同的知识点，北师大版教材用了同一个素材，是生活中常见的图形，教师A和教师B均用了两种不同的素材。对于认识轴对称图形，教师A选用学生熟悉的生活中的实物图片，教师B选用学生熟悉的具有民族特色的实物图片。对于认识对称轴，教师A选用规则的平面图形，教师B选用不规则的图形。雖然两位教师选用的实物和图形各异，但稍做比较，就能看出两位教师相同的教学理念。教师A和教师B都非常重视学生已有的生活经验，运用生活素材创设教学情境。教师A给出实物的一半，让学生猜猜是什么物品，并引发学生思考：有的实物能猜得出，有的猜不出，为什么呢？教师B让学生欣赏蕴含少数民族文化的族徽、建筑、乐器、服饰等不同的实物，并引发学生思考：这些物品有什么共同特点？两位教师将抽象的数学知识生动形象地呈现在学生面前，使他们在已有生活经验的参与下理解其中蕴含的数学知识。接着，两位教师呈现了第二组素材——几何图形，实现了从生活到数学的自然过渡，让学生在初步感知的基础上探索和验证轴对称图形的特征，使学生循序渐进地加深对轴对称图形基本特征的认识和理解。

叶圣陶先生说过，教材无非是个例子。具有轴对称图形特征的实物和平面图形不计其数，为何北师大版教材和两位教师选择这几种图形作为例子呢？我们再来品味一下两位教师对教材的研读和独具匠心的设计。轴对称图形的基本特点是对折后图形两边能完全重合，它不受图形的形状和对折的方向影响。三者提供的图形有着典型的代表性，如方正的“囍”字、形状各异的花朵和侗族鼓楼等。并且，图形摆放的位置也十分讲究，如叠加的三角形图、花朵、蝴蝶、长鼓。教师引导学生进行比较，不论是像衣服、长鼓一样有着平滑的外观，还是像花朵、鼓楼一样有着不平整的边缘，对折后图形两边都必须完全重合。不论是像心形、裙子、鼓楼这样左右对折，还是像叠加的三角形图、蝴蝶、长鼓那样上下对折，或是如花朵那样斜着对折，只要是对折后图形两边完全重合即为轴对称图形。花朵、蝴蝶、长鼓其实都可以正着摆放，然而仅是一个方向的转换，就可见教师的用心和功底，教师在研读教材的基础上，紧扣概念的本质属性，选择贴近学生生活和数学认知的教学素材，让学生通过观察去除概念的非本质属性，获得直观经验。

教学素材是教师教和学生学的重要载体，教学素材的选择体现了教师对该知识教学目标、教学过程的理解，也直接决定了学生对该知识的兴趣程度，及其对内部表征、认知结构的建构。因此教师要在仔细研读教材、把握其内涵的基础上，对教学素材进行重组和创新。

二、运用反例辨析，加深概念理解

在概念教学中，教学素材除了可以选择正例，还可以适当运用反例供学生研讨辨别，加深学生对概念的理解。对于轴对称图形的教学，教师A选择平行四边形作为反例，教师B选择教材上的图形作为反例。这两个反例极具代表性，因为将这两个图形从中间对折，看上去左右两边形状是一样的，实际上对折后两边并不重合。特别是图形，更利于学生观察和辨析。从中间对折，左右两边都有，但一个高一个低，并且两个小黑圈方向都朝左，因此对折后不能重合。通过比较，学生明晰了两边一样并不代表完全重合，懂得区分轴对称图形的非本质属性和本质属性，从而掌握研究对象的本质特征。

在教学中运用反例，从心理学的角度来看，这是一种比较，有比较才有鉴别。值得注意的是，教师要合理安排反例出现的时机，最开始提供给学生观察的实物材料必须是具有代表性的正例，否则会给学生的分辨和理解带来干扰，甚至会强化学生对反例的记忆，不利于学生对本质属性进行理解。

三、依托直观操作，经历概念形成的过程

心理学研究表明：儿童从他们与周围物体作用的活动中获得理解。单纯的几何概念对学生来说是比较抽象的，需要学生在观察、触摸等动手操作的过程中积累数学活动经验，并通过比较、分析、归纳等思维活动抽象、概括出几何概念。这个理念随着新课程改革的推进已经深入人心。为了让学生深刻理解和掌握轴对称图形的特征，教师A和教师B都设计了操作活动，采用“做中学”，引导学生在自主、合作、探究的过程中分析、比较各种例子的相关属性，积累丰富的数学活动经验，让学生亲身经历轴对称图形概念的形成过程。

“做中学”是教师在课堂上常用的教学方法，但需要注意的是，盲目的、缺乏思考的动手操作不是有效的操作。教师在教学中通常会发现，学生在动手操作的过程中，往往容易被学具的形状、色彩等外部特征所吸引，这便失去了操作的意义。教师应引导学生学会在操作中观察，始终保持有意注意。教师A引导学生动手折一折时让学生判断哪些图形是轴对称图形，如果是轴对称图形最多能找到它的几条对称轴，哪些圖形不是轴对称图形，并说明理由。教师B在学生动手操作前提出活动要求：1.沿一条直线对折图形，摸一摸，看一看;2.把你的发现告诉你的同桌。两位教师提出的问题虽然不同，但共同点是提出的任务均具体、明确，让学生有的放矢地去操作。教师A的学生会在操作中观察所折图形是否完全重合，以此做出判断。教师B的学生会在操作中观察对折后的图形有什么特点。观察可以促进学生思考，学生的动手操作过程其实就是一个在操作中思考、在思考中操作的活动过程。

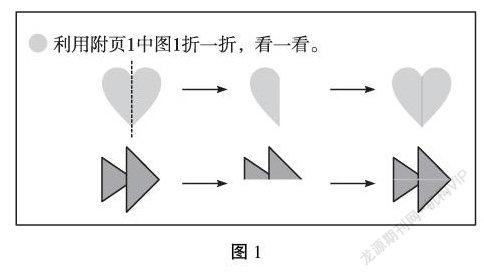
同样地，北师大版教材“轴对称（一）”的学习目标中也明确提出：通过观察和操作活动，初步认识轴对称图形。教材中呈现了如图1所示的轴对称图形的学习过程。

教材中的“利用附页1中图1折一折，看一看”，“折”是动手操作，“看”即观察。学生首先通过两个图形对折后能够重合确认前面通过观察得到的结论——两边一样，然后再打开观察完整的图形。教学中教师通常会重点让学生观察对折后图形两边是否完全重合，往往忽略“再打开观察完整的图形”这个环节，而这恰恰是个关键环节。在教学实践中，我们发现，在这个环节上的观察缺失，会导致在练习中判断这个图形是否为轴对称图形时，近三分之一的学生出错。因为不论是教材呈现的文字“这些图形从中间分开，两边一样”，还是教师的表述，都会用上“两边一样”这样的话语。那么两边一样等同于完全重合吗？教师不妨引导学生再打开观察完整的图形，认真、仔细地观察折痕的两边。通过观察，学生会发现中间的折痕把图形分成一样的两部分，然而方向是不同的。如轴对称图形的心形图案，其对称轴两边的弧线一个是左边凸起，一个是右边凸起;对于叠加的三角形图，其对称轴两边一个是锐角在上，一个是锐角在下。教师要引导学生抓住关键点和细节去观察，发现轴对称图形隐蔽的特征，理解两边一样是指形状一样，方向却正好相反。

仔细品味两位教师的课例，我们可以发现其背后遵循着相同的教育教学规律。对“轴对称（一）”课例进行比较和分析，有助于我们思考和总结几何概念的教学策略，并将其应用于教学中，这也正是同课异构聚焦“同”分析的价值所在。

（责任编辑：罗小荧）