HPM视角下的项目化数学教学设计

李德虎 汪晓勤

【摘 要】HPM视角下“长方体直观图的画法”的教学以“选美大赛—古书修订—厚积薄发—建章立制—牛刀小试—画龙点睛”为主线，重构式运用数学史，运用项目化学习理念创设情境，让学生化身为小数学家进行“古书修订”，在小组合作探究中讨论制订长方体直观图画法的三条规则，形成“斜二测”画法，再现了“斜二测”画法诞生的过程。本节课是项目化学习与HPM视角下课堂教学相结合的一次尝试。

【关键词】HPM;“斜二测”画法;项目化学习

【作者简介】李德虎，上海市新杨中学科研处主任，高级教师，HPM工作室成员，主要从事初中数学教学研究;汪晓勤，华东师范大学教师教育学院教授、博士生导师，主要从事数学史与数学教育研究。

【基金项目】上海高校“立德树人”人文社会科学重点研究基地之数学教育教学研究基地研究项目——数学课程与教学中落实立德树人根本任务的研究（A8） “长方体直观图的画法”是沪教版初中六年级数学教科书第八章“长方体的再认识”第2节的内容，学生在小学阶段已经认识了长方体，会根据公式计算长方体、正方体的表面积和体积，对长方体的直观图也有初步的认识。《上海市中小学数学课程标准（试行稿）》指出，学生要熟悉长方体直观图的某一种常用图形，会画长方体的直观图（采用“斜二测”画法）[1]。本节课属于立体几何的启蒙课，为学生后续学习长方体中棱与棱、棱与面和面与面的关系乃至高中立体几何打下基础。

在教学实践中，教师通常直接告知学生长方体直观图的画法，并带领学生一起按步骤用“斜二测”画法画长方体，而对于为何要将上下底画成一个内角为45°的平行四边形且取宽为实际长度的一半，均不做说明[2]。在课堂上，学生难免会对“斜二测”画法的规定产生疑问。鉴于此，我们希望从HPM的视角，重新设计“长方体直观图的画法”教学内容，并付诸实施。本节课拟订的教学目标如下。

（1）理解“斜二测”画法的合理性，会用“斜二测”画法画长方体，培养学生初步的空间观念和空间想象能力。

（2）经历“斜二测”画法的形成过程，体会其中的研究方法。

（3）对话历史，提升学生数学学习的自信心，形成动态的数学观，体会数学背后的理性精神。

一、数学史料及其运用

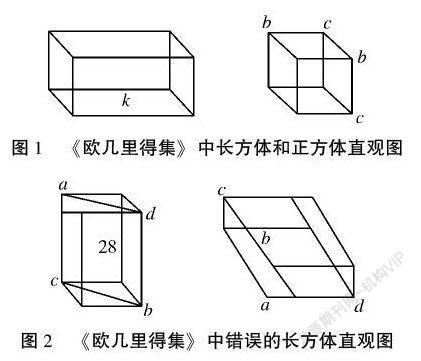
在16世纪的几何书籍中，已经普遍使用平行四边形来表示长方体的六个面，在1509年出版的《欧几里得集》中[3]，长方体和正方体直观图的画法如图1所示。可见，当时人们已经采用斜投影画法来画长方体的直观图，其中平行四边形的一个内角近似取45°，但宽并没有取实际长度的一半。特别在正方体直观图中，长和宽保持两两相等关系，即上、下、左、右四个面为菱形。

书中还出现了一些错误的长方体直观图，如图2所示。

1532年，法国数学家费奈乌斯（O.Finaeus）在《数学之源》[4]中给出的长方体画法与《欧几里得集》类似，将正方体的上、下、左、右四个面画成菱形，如图3所示。1564年，意大利数学家巴托利（C.Bartoli）在《测量之术》[5]中沿用了同样的画法，保留正方体长、宽和高的实际长度，看起来就像一般的长方体，如图4所示。

直到17世纪，正方体的画法有了明显的改进，如1624年，意大利数学家博莫多罗（Pomodoro）在《实用几何》中画的正方体直观图就不再保持长和宽相同[6]，但是图中的宽并没有取实际长度的一半，而是取实际长度的23，如图5所示。

到19世纪末，关于长方体直观图仍未有统一的规范画法，例如1899年，米尔恩（W.J.Milne）在《平面与立体几何》[7]中将上、下底面的宽取为实际长度的23，一个内角接近30°，如图6所示。

可见，在将近400年的漫长时间里，数学教科书基本采用斜投影的轴测图来画长方体，但表示上下底面的平行四边形的邻边大小关系和一个内角的大小并不统一，宽处于实际长度的13到实际长度相等之间，一个内角处于30°和60°之间。

直到1916年，美国数学家贝茨（W.Betz）和韦布（H.E.Webb）在其《立体几何》[8]中给出了斜二轴测投影（简称“斜二测”画法）的作图法，作者称这种投影是一种“令人满意的投影方式”，如图7所示。

数学史告诉我们，长方体直观图的“斜二测”画法经历了漫长的探索过程，其实是一种规则的制订，是数学家在讨论中“约定俗成”的。教师可以采用探究式教学法，让学生在讨论中形成画法规则，重现“斜二测”画法规则制订过程，揭示学生画法的历史相似性。

二、教学设计与实施

根据数学史料，本节课教学设计运用项目化学習的理念，分为选美大赛、古书修订、厚积薄发、建章立制、牛刀小试和画龙点睛六个部分。以四本古书修订为驱动性问题，引导学生小组探究，讨论制订长方体直观图的画法规则，形成核心知识“斜二测”画法。

课前，教师要求学生画出边长是3cm的正方体。教师在对学生的画法进行分析后，发现大部分学生都是采用斜投影画法，并得到相应的数据。

课上，教师首先播放HPM微视频，介绍历史上人们对长方体画法的探索，其中包括中国古画（宋徽宗《文会图》）中桌子的画法、达·芬奇绘画作品中透视画法等。本节课介绍的画法为长方体直观图画法的一种，如图8所示，从而引入本节课的课题。

（一）选美大赛

教师让每个小组的学生从各自小组作品中选出最美的一幅图，再通过希沃投屏展示出来，如图9所示。

师：下面请大家一起选一选哪一幅图最美？

不同小组的学生表达了不同的看法。

师：为什么大家没有形成统一的意见？

生：因为没有评价的标准。

师：很好，那么这节课我们就一起来制订这个“选美”标准。

【设计意图】通过选美大赛，让学生明白制订长方体直观图画法的必要性，为后面探究长方体“斜二测”画法的三个规定做铺垫。此外，部分学生的画法和历史上教科书的画法也相似（如图9c），揭示出学生长方体直观图画法的历史相似性。

（二）古书修订

教师用PPT展示四本古书，如图10所示，让学生对照自己画的正方体和古代数学家画的正方体。

師：四本古书画的都是边长为3cm的正方体，但各不相同，请各位小数学家们帮忙修订这四本古书，以便于后人阅读。

【设计意图】教师事先对史料进行整理，发现很多书籍中都涉及正方体的画法但又不尽相同，所以截图保存并缩放图像，使每个正方体的长均为3cm，高也为3cm制成学习单（学生课前画的正方体的直观图长和高均为3cm）。借助历史相似性原则和项目化学习的理念，教师让学生化身为修订古书的数学家，在修订古书的情境中展开探究式学习。

（三）厚积薄发

本环节主要学习平面的概念和表示法，以及长方体直观图的概念，为学生后续的学习探究做准备。

师：长方体有六个面，我们要研究长方体的直观图，首先来看看怎么画平面。生活中有哪些实例给我们以平面的形象？

生：地面、黑板、桌面和平静的湖面。

教师结合图11介绍古代数学家对“平面”的定义。

师：数学中，平面是平的，无边无沿，我们可以用一个平行四边形来表示它。特别地，把水平放置的平面画成一边是水平位置，另一边与水平线所成的角为45°的平行四边形，如图12，表示为平面ABCD或平面α。

师：我们把空间图形画在平面内，使得既富有立体感，又能表达出图形主要部分的位置关系和度量关系的图形叫直观图。

师：结合图13，同学们想一想画长方体直观图的关键是什么？

生1：斜着画。

生2：调整长度。

【设计意图】教师借助历史上几位数学家对“平面”的定义，引出平面画法及表示法。同时，教师给学生补充直观图的概念，让学生思考长方体直观图的两个关键因素，为后面画法规则的制订提供依据。

（四）建章立制

教师出示图10，要求学生借助直三角尺和量角器对学习单上四幅图进行测量，并回答以下问题。

（1）正方体的边长（长、宽、高）应画为多少厘米？

（2）底面平行四边形中的锐角取多少度？

（3）看不见的棱如何画？

学生把研究结果投屏到屏幕上。教师归纳学生的讨论结果：看不见的棱用虚线表示;关于底面平行四边形中的锐角取多少度的问题，学生建议取45°比较方便;关于长和高大家都觉得应取3cm;关于宽应取的长度，学生主要有两种意见，一部分学生认为应取实际宽的一半为1.5cm，另一部分学生认为应取2cm。

师：请大家想一想，如果老师给的正方体棱长是2.6cm，同学们觉得宽取多少才合适呢？

生：取一半，1.3cm比较好画。

师：请同学再看一下课前你们画的棱长为3cm的正方体的统计图（如图14和图15所示）。

师生一起归纳画长方体直观图的规则：（1）长方体直观图中，长和高不变，宽取实际长度的一半;（2）底面平行四边形中的锐角取45°;（3）看不见的棱用虚线表示。

师：这种画长方体直观图的方法我们称为“斜二测”画法。在中国古代，画家通过实践发现上述规则兼顾立体感和位置关系，是一种无意识的几何实践。数学家贝茨和韦布综合前人的画法称“斜二测”画法为“令人满意的投影方式”。课后请大家根据我们制订的“斜二测”画法，在选出的五幅正方体直观图中选出最美的一幅，并在学习单上完成对四本古书的修订。

教师用PPT展示宋徽宗的《文会图》和《立体几何》（1916年）中的正方体。

（五）牛刀小试

通过练习巩固新知，学生掌握了本节课的重点——长方体直观图的画法。在教师的引导下，学生完成以下任务：画长4cm、宽3cm、高2cm的长方体ABCD-EFGH直观图。在课堂练习中，教师让学生指出《欧几里得集》中长方体存在的问题（如图2）。

（六）画龙点睛

师：通过本节课的学习，大家有什么收获？

生1：我掌握了平面画法和表示法。

生2：画长方体直观图的时候，宽应取实际长度的一半，平行四边形中的锐角应取45°。

生3：画长方体直观图看不见的棱用虚线表示。

生4：“斜二测”画法的规定是讨论制订的，既体现了图形的立体感，又保持了位置关系和度量关系。

师：同学们说得很好，老师这里给出一个关键字：序，同学们有什么感悟？

生5：平面的表示字母要按照顺时针或者逆时针顺序。

生6：用“斜二测”画法画长方体要注意画图的顺序。

师：对的，现实的世界本来是混沌无序的，数学学习就是帮助我们在无序的世界发现规律，建立规则或标准，这样我们的世界将变得更加和谐。

教师通过课堂小结，点明了本节课的核心内容——“序”的建立，让学生明白这个“序”，既包括平面和长方体表示法中字母之序、“斜二测”画法之序，也包括长方体直观图画法的形成之序。借助数学知识，学生理解了建立现实之“序”的意义。

三、学生反馈

基于本节课，笔者对班级学生进行了前测和后测。在前测中，笔者通过问卷调查了解到：96.4 的学生采用斜投影的轴测图来画棱长是3cm的正方体，3.6 的学生采用透视画法;全班学生画的长和高都取3cm，宽的取值和平行四边形的夹角如图14和图15。43.9 的学生没有画被遮挡的三条棱，18.9 的学生用实线来画被遮挡的三条棱，37.2 的学生用虚线来画被遮挡的三条棱。可见，学生初步了解长方体的轴测图画法，但对于宽的取值、平行四边形的夹角和如何处理被遮挡的三条棱没有形成统一的意见。

在后测中，笔者对全班28名学生进行问卷调查，旨在了解学生对本节课教学的感想与建议。在问卷调查中，100 的学生能正确的采用“斜二测”画法画出棱长是3cm的正方体直观图，完成“古书修订”任务。

学生关于这节课与平时课堂教学最大的不同感受统计如图16所示。

关于数学史（“古书修订”）有没有帮助你理解“斜二测”画法合理性的问题，96.4 的学生的回答是肯定的，学生认为“这些图也体现了我们自己作图的问题”“我们只有不断和古书对比，才能研究出‘斜二测画法”“通过古人不同的画法拟定一个方便的值”“通过与古书对比，我发现‘斜二测画法更容易画且更美观”“古书中的画法为‘斜二测画法奠定了基础，‘斜二测画法汲取了古书中画法的优点”等。

在长方体“斜二测”画法中，为什么宽要取原来长度的一半、平行四边形一个夹角为什么画成45°？学生的回答如图17所示。

四、结语

从教师教的角度，本节课构建了三个层次：“就题论题”“就题论法”“就题论道”。（1）在“就题论题”的层面，本节课的核心是学会用“斜二测”画法画长方体的直观图。在教学中，教师通过板演，按照四个步骤引导学生一起画图，通过课后反馈发现，全班学生掌握了这种画法。（2）在“就题论法”的层面，本节课借助项目化学习和数学史料构建情境，借助历史相似性原则，让学生一起讨论制订长方体直观图画法的规则，真实还原“斜二测”画法产生的过程。（3）在“就题论道”的层面，教师课前设计“选美大赛”和“古书修订”两个环节，引发学生对“选美标准”和“修订规则”的制订，进而形成三条规则，得出“斜二测”画法，在最后的小结中，用一个“序”字结尾，使学生体会到数学学习让“无序”的世界变得“有序”。

从学生学的角度，本节课践行了数学教育家弗赖登塔尔的数学教学原则。课前学生的“数学现实”为会用斜投影法画长方体直观图，但没有形成“斜二测”画法;教师从学生的“数学现实”出发，引导学生“数学化”活动体验[9]，设置“选美大赛”和“修订古书”两个情境;通过合作探究引导学生进行“再创造”，制订长方体直观图的画法三条规则，形成“斜二测”画法;整节课贯穿数学“思想实验”原则，教师设置的大部分问题都是开放性问题，没有固定的答案，实现了数学知识的自我构建。

本节课运用数学史重构式开展教学，让学生经历“斜二测”画法的产生过程，构建了知识之谐;借助“古书修订”任务驱动学生开展讨论，营造了探究之乐;通过数学与艺术的联系、长方体直观图选美的活动，展示了文化之魅;通过呈现古今长方体直观图画法的演进，让学生形成动态数学观，达成德育之效。

此外，本节课融合HPM微视频、希沃投屏等教育信息技术，带动数学史内容的可视化呈现和情景创设，引发学生探究，是项目化学习与HPM视角下的课堂教学相结合的一次有益尝试。

參考文献：

[1]上海市教育委员会.上海市中小学数学课程标准（试行稿）[M].上海：上海教育出版社，2004.

[2]王慎洁.以混合式教学落实差异化教学的探索：以“长方体直观图的画法”一课为例[J].现代教学，2021（增刊1）：146-147.

[3]EUCLID.Euclidis megarensis[M].Venezia：A.Paganius Paganinus，1509.

[4]FINAEUS O.Protomathesis[M].Parisiis：Impensis Gerardi Morrhij & Ioannis Petri，1532.

[5]BARTOLI C.Del modo di misvrare[M].Venetia：Per Francesco Franceschi Sanese，1564.

[6]POMODORO G.La geometria prattica[M].Roma：Angelo Ruffinelli，1624.

[7]MILNE W J.Plane and solid geometry[M].New York：American Book Company，1899.

[8]BETZ W，WEBB H E.Plane and solid geometry[M].Boston：Ginn & Company，1916.

[9]王晓杰.数学文化教学对小学生数学抽象素养的影响研究[D].重庆：西南大学，2017.

[10]汪晓勤.基于数学史的数学文化内涵课例分析[J].上海课程教学研究，2019（2）：37-43.

（责任编辑：陆顺演）