精密包装弹性支撑缓冲系统振动特性修正模型及分析
2021-12-02严国平彭震奥于道航周宏娣杨小俊
严国平,彭震奥,钟 飞,于道航,周宏娣,杨小俊
(湖北工业大学 机械工程学院,武汉 430068)
缓冲包装系统可用来吸收外部的能量,起到保护产品的作用,被广泛应用于产品包装运输过程中。由于缓冲包装系统在运输过程中道路条件的影响,缓冲包装系统通常会受到垂直于行驶方向(纵向)的振动激励,这也是目前减振研究的主要方向。另外,实际工程应用中的缓冲减振结构种类较多,国内外学者对各类缓冲包装力学模型进行了广泛的探索。
王蕾等[1]以悬挂式缓冲包装为研究对象,探讨该缓冲包装系统的冲击特性;李辉等[2]在考虑易损件的情况下建立了二自由度的悬挂缓冲包装力学模型并在跌落环境下对其跌落防护做出了评价;李宏卫[3]给出一种新的算法用以评估缓冲包装力学模型强非线性并进行了试验验证。郝蒙[4]细化了易损件的形式,针对性地讨论了易损件结构为悬臂梁的缓冲包装特性;Sakar[5]采用欧拉-伯努利梁假设法对包含悬臂梁的缓冲包装进行了研究,讨论了对系统固有频率的影响。卢富德等[6-8]以单层瓦楞纸板研究为基础,提出了多层瓦楞纸板间的动力学模型并进行了响应特性的计算;於崇铭等[9]给出了弹药运输三自由度缓冲包装模型并建立其在简谐激励下的振动力学微分方程;Gao等[10]建立了半正弦加速度脉冲下的缓冲包装系统动力学方程,研究了考虑产品质心偏移的旋转与平移耦合问题;卢富德等[11-12]建立了可降解餐具碗在缓冲包装作用下的有限元模型,研究了受冲击载荷的泡沫包装餐具碗的应力分布及抗冲击能力。以上这些研究主要针对缓冲包装系统在工作振动方向进行分析,较少考虑侧向缓冲系统对振动特性的影响。而对于精密包装来说,侧面包装缓冲要求较高,横向弹簧缓冲系统对于纵向振动激励有较大影响,对其进行振动特性分析时如果不考虑侧向缓冲系统则可能会使系统振动分析误差较大,达不到精确分析的要求。
有鉴于此,本文引入横向弹簧的径向刚度作为计算修正参数,较全面地对精密包装弹性支承缓冲系统振动特性进行深入研究,并通过试验对该理论修正模型进行了验证,为精密包装弹性支撑缓冲系统振动特性数值精确分析提供依据。
1 精密包装缓冲系统减振分析修正模型
1.1 弹性支撑缓冲系统的力学模型
某精密包装内部减振器分布,如图1所示。将货物及其包装箱以及安装底板看作整体,可得到简化力学模型如图2所示。以物块质心为参考点,坐标系建立于质心处,质心的运动由沿坐标轴的平动位移x,y,z以及绕各坐标轴的转动角度α,β,γ组成。同时系统中的等效刚度系数为kai,kbi,kci,kdi,阻尼系数分别是cai,cbi,cci,cdi,i的取值分别为0,1,2,i的编号与弹簧阻尼的固定端编号一致。设包装产品的质心为M′,其到面ADHE的距离为w1,到面BCGF的距离为w2,到面EFGH的距离为h1,到面ABCD的距离为h2,到面DCGH的距离为l1,到面ABFE的距离为l2。

1.集装箱;2.货物安装底板;3.减振器;4.货物。
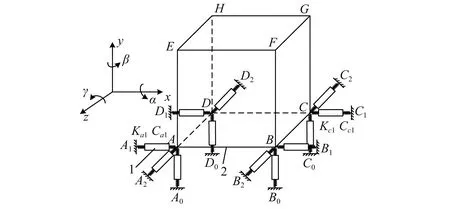
图2 力学模型
本文采用能量法研究质心M′的六自由度运动。为了获得弹簧的弹性势能,需先对A,B,C,D四个点的运动位置与质心M′的运动位置之间存在的关系进行准确判断。由于所述模型的转动是绕过质心的坐标轴转动,可先计算出模型绕DH棱转动时的坐标变化,再进一步完成绕M′点旋转的位置推算,如图3所示。

图3 转动模型
图3中ABCDEFGH为转动前位置,A′B′C′DE′F′G′H为绕DH轴旋转了角度σ之后的位置。通过计算转动后的实际位移及其在X轴的投影,可推出旋转前后各几何边在X轴投影的差值,再运用右手定则可求得图2中模型下方四个支撑点的坐标[13]为
(1)
系统的总动能T,包括平动动能以及转动动能,可表示为
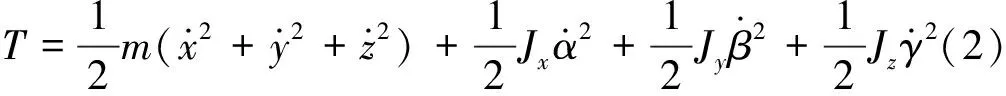
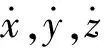
系统的总弹性势能V为X轴向弹性势能Vkx,Y轴向弹性势能Vky以及Z轴向弹性势能Vkz之和,可表示为
V=Vkx+Vky+Vkz
(3)
其中,Vkx,Vky,Vkz的表达式分别为
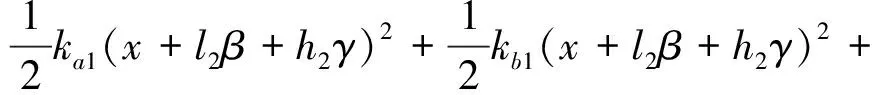
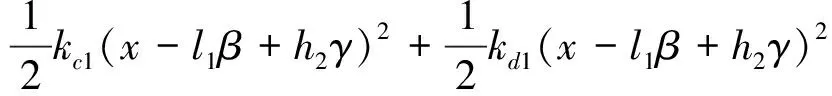
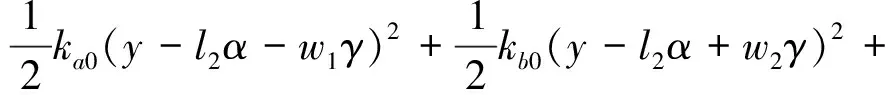
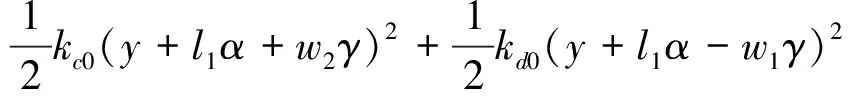
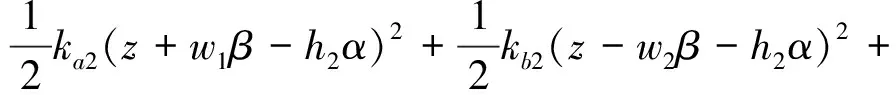
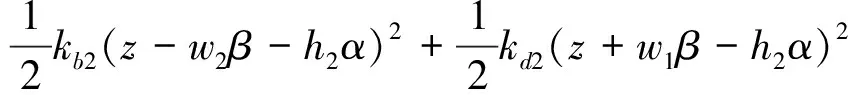
系统的总耗散能U为X轴向耗散能Ucx,Y轴向耗散能Ucy以及Z轴向耗散能Ucz之和,可表示为
U=Ucx+Ucy+Ucz
(7)
其中,Ucx,Ucy,Ucz的表达式分别为
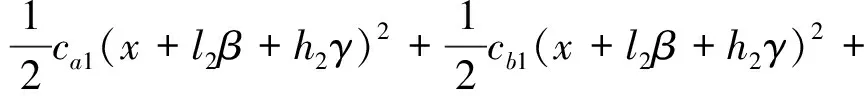
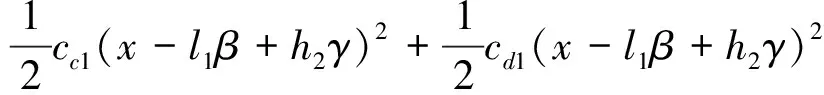
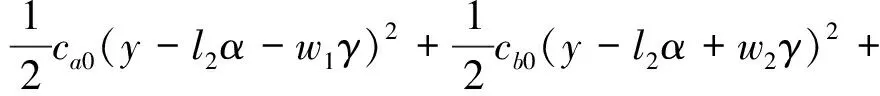

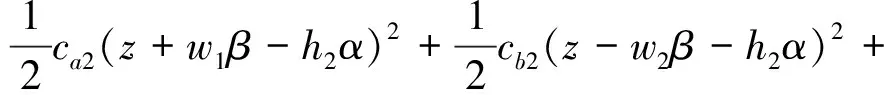
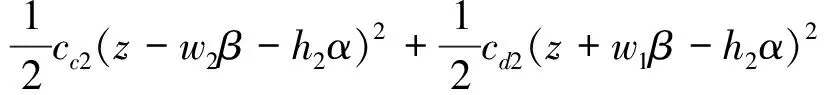
整个包装缓冲系统总能量E包含物块运动总动能T,弹簧产生弹性势能V以及阻尼构件产生的耗散能U。其能量方程[14]表达式为

(11)
为简化模型,设定X,Y,Z轴向的各弹簧系数各自相等,如式(12)所示
(12)
将式(11)进一步简化得到各轴向安装的弹簧阻尼相同时的能量方程为

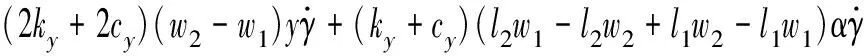
进而可得如下方程
(14)
(15)
(16)
1.2 考虑弹簧径向刚度的修正模型
式(15)未考虑横向缓冲系统对Y方向振动系统的影响,忽略了X,Z方向弹簧对Y方向振动产生的作用。这里引入X,Z方向弹簧的径向刚度作为计算修正参数代入式(15)中,以期获得考虑横向弹簧影响的精密包装弹性支承缓冲系统振动的精确计算模型。
弹簧径向刚度可由弹簧轴向刚度与轴挠度计算得到。轴向刚度k的计算式为
(17)
式中:d为弹簧线径;Gt为弹簧材料的剪切模量;D为弹簧内径与外径的平均值;n为有效圈数。
弹簧在载荷P的作用下的轴向挠度f
(18)
当两支承面的接触方式为弹性接触时,且两支承面能发生相对转动,径向刚度kr计算公式为
(19)
式中:H为弹簧在载荷P的作用下两支承面间的高度;i为载荷P对弹簧径向变形的影响因子,其表达式为
(20)
系数i也可根据参考文献[15]进行查找。
设krai,krbi,krci,krdi为X,Z向弹簧的径向刚度,i取1和2,设定所有径向刚度相等,缓冲系统Y轴向振动微分方程式(15)可修正为
(4ky+8kr)y+(2ky+4kr)(l1-l2)α+
(2ky+4kr)(w2-w1)γ=0
(21)
整个包装缓冲系统振动方程可表示为
(22)
式中:M为包装缓冲系统的整体质量矩阵;C为包装缓冲系统的整体阻尼矩阵;K为包装缓冲系统的整体刚度矩阵;X为包装缓冲系统的整体广义位移向量。
包装缓冲系统的整体质量[M]表示为
(23)
包装缓冲系统的整体阻尼矩阵[C]表示为
包装缓冲系统的整体刚度矩阵[K]表示为
(25)
2 具体算例
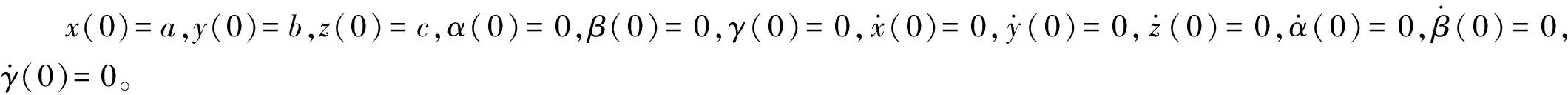
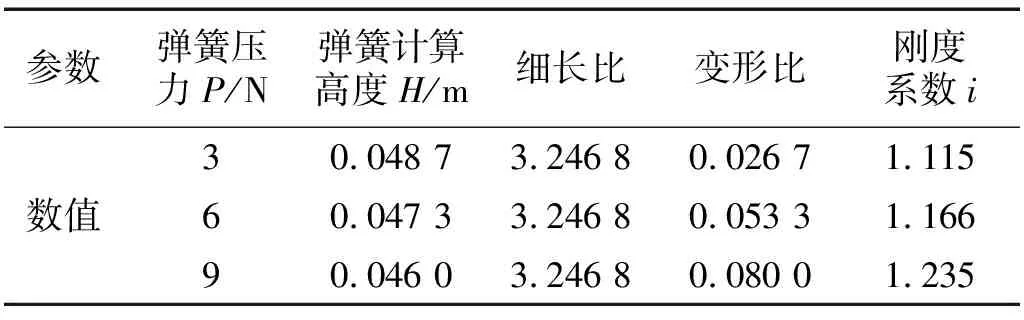
表1 径向刚度参数表

表2 工况参数
图4为工况一下不同侧向弹簧压缩力时y向位移变化结果曲线,图4为工况一下径向刚度系数变化下幅频曲线。
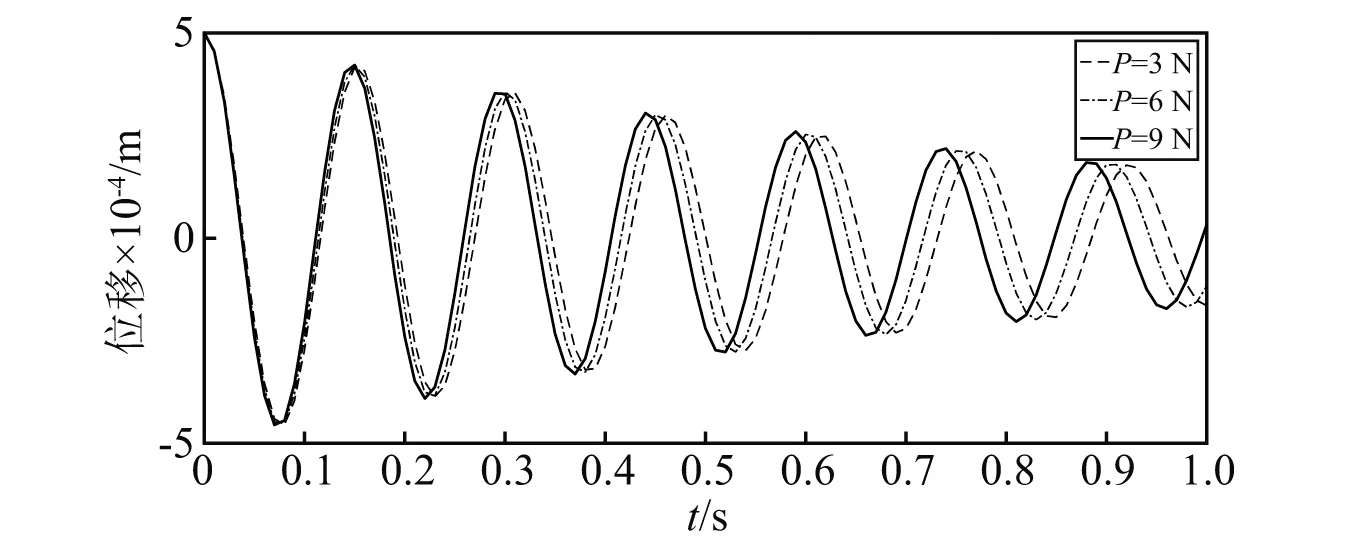
图4 工况一时Y向位移变化曲线
从图4中可以看出,当横向弹簧减振器上压缩力P发生变化时,由于其压缩引起弹簧径向刚度的差异,使得货物包装箱的固有频率随其产生变动;当横向弹簧减振器所受轴向压缩力增大时,缓冲系统在Y向的固有频率也会同步增大。这一规律表明:若产品运输时主要遭受高频激励时,可考虑对产品包装箱两侧降低压紧程度,降低其固有频率,防止出现共振现象;当产品在遭受低频激励状态时,可适当增大压紧力,保护集装箱内部产品。
图5表明,径向刚度系数i越大,缓冲包装系统共振幅值响应越大。为避免短暂共振带来的危害,应适当降低精密缓冲包装系统固有频率值以保护被包装的产品。进一步地将本文所提出的修正模型所得Y轴向固有频率与未考虑横向缓冲系统影响的计算方法所得结果进行对比,如表3所示。
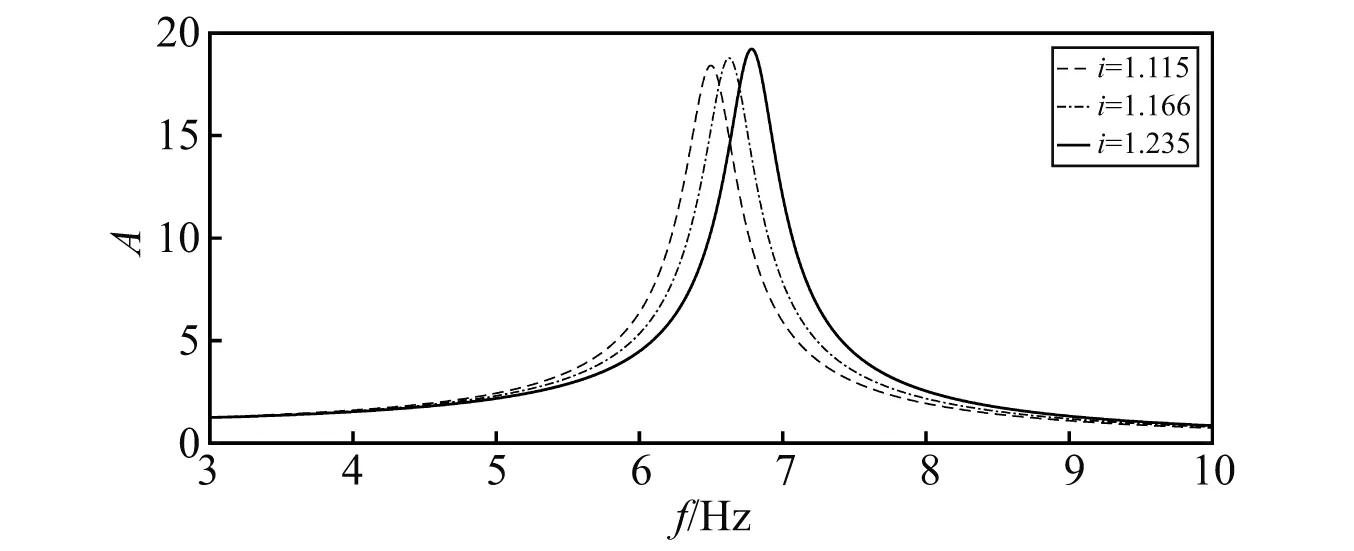
图5 工况一时径向刚度系数变化下幅频曲线
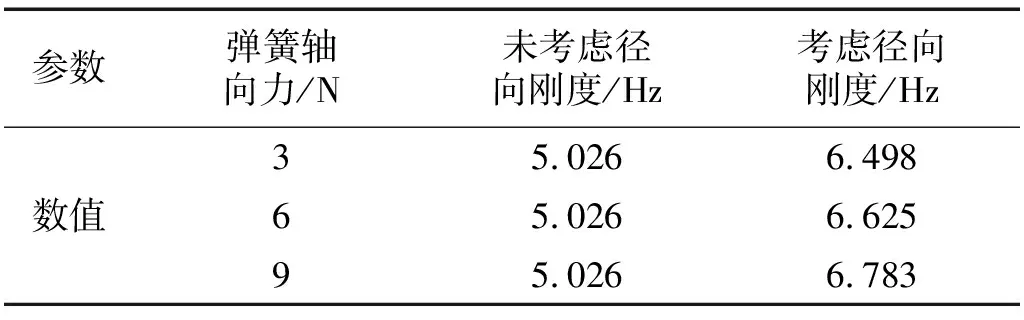
表3 Y轴向固有频率值
由表3中数据可以看出,理论计算时,未考虑横向弹簧径向刚度时,缓冲系统固有频率没有变化。而考虑横向弹簧径向刚度时,精密缓冲包装系统固有频率计算结果产生了较大的差异,且横向弹簧轴向预压力越大,缓冲系统Y轴向固有频率越高。这说明对于侧面包装缓冲要求较高的精密包装来说,横向缓冲系统对其纵向振动特性的影响不能忽略。
图6中,工况二时精密包装缓冲系统在X,Z轴向的加速度峰值更小。虽然此时依然存在加速度变化不稳定的现象,但相较于工况一,其加速度的变化差值更小。在初位移状态下,因加速度变化过大导致的产品损坏的几率在一定程度上低于工况一。

图6 两工况下包装缓冲系统加速度对比曲线
工况二时质心位置将偏向于图2中的C点,为满足安装准则,以C点处Y轴向的弹簧刚度kyc为变量,讨论其对振动响应的影响。分别令kyc为1 000 N/mm,2 000 N/mm,3 000 N/mm,Y轴向振动加速度影响变化如图7所示。
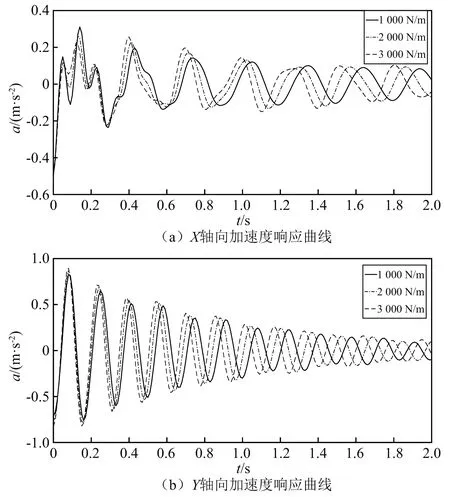
图7 工况二时C点弹簧刚度非对称时响应曲线
由图7可知,工况二时C点Y轴向刚度增加,产品包装箱的Y轴加速度响应产生相位差,加速度幅值随之增加。此时其X轴向加速度响应存在一段不稳定的波动,该波动会随C点Y轴向刚度的增加而减少。因此,工况二下,为平衡集装箱内产品的各向加速度响应,不应无限制地增加或减少单一支承点的减振器刚度,否则会对其他方向产生不利影响。
3 试验研究
精密包装缓冲系统振动试验平台,如图8所示。测试用振动实体模型,如图9所示。选用的弹簧变形量设计为20 mm左右,其参数如表4所示。振动试验台选用DY-300-3电动振动试验台(苏州试验仪器总厂),除原厂配备的数据采集系统外,运用LabView软件编制了相应的附加数据采集系统,用以对采集的数据进行比较。对振动台进行标定,原振动台自身存在2.34%的输出频率误差。使用瞬干胶将传感器与物块上端黏合,测量其纵向加速度数据。
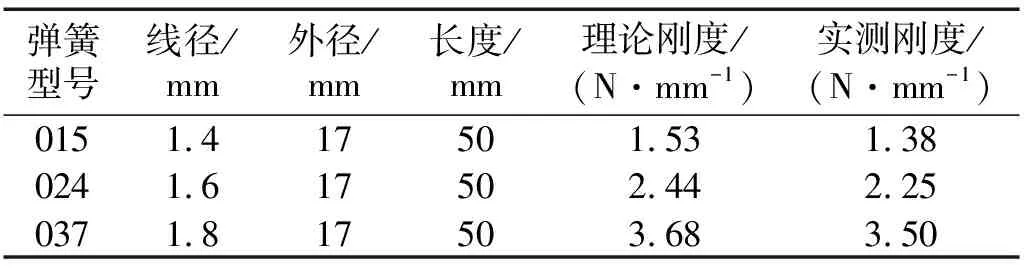
表4 弹簧参数表

1.缓冲包装振动系统;2.振动平台;3.控制系统;4.采集系统。

1.物块;2.弹簧减振器;3.振动台台面;4.夹具板;5.角铝固定件。
各轴向弹簧刚度kx=ky=kz=k时,对其进行横向弹簧在无压紧力时进行扫频试验,其结果如图10所示。推导所得的理论值如图11所示。
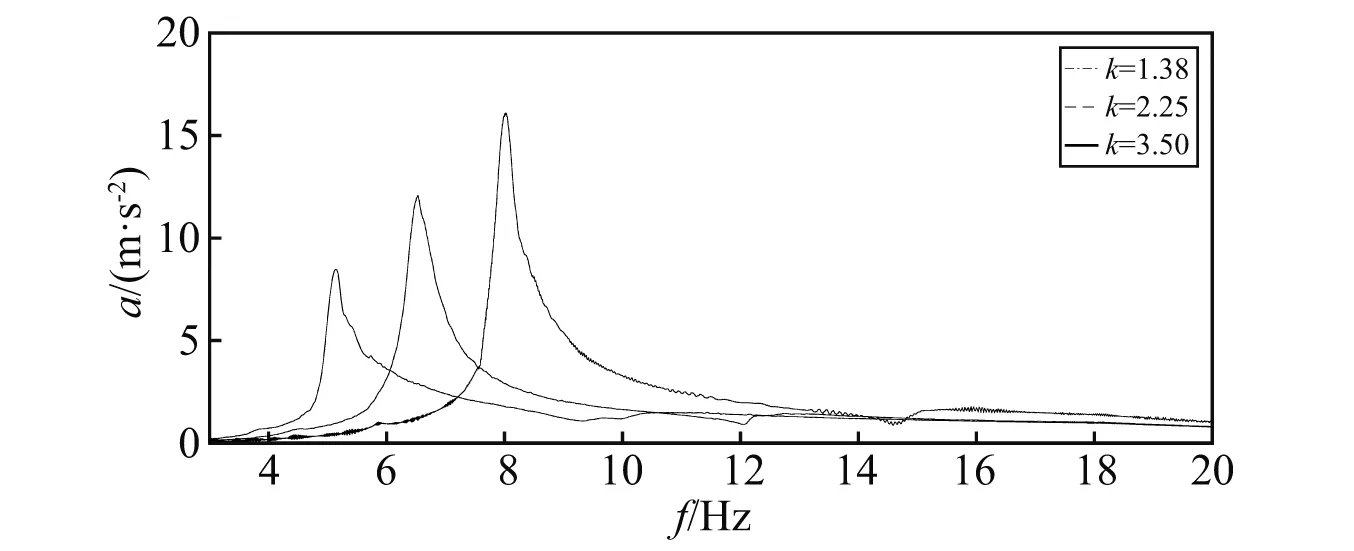
图10 横向弹簧无压紧力时扫频试验曲线
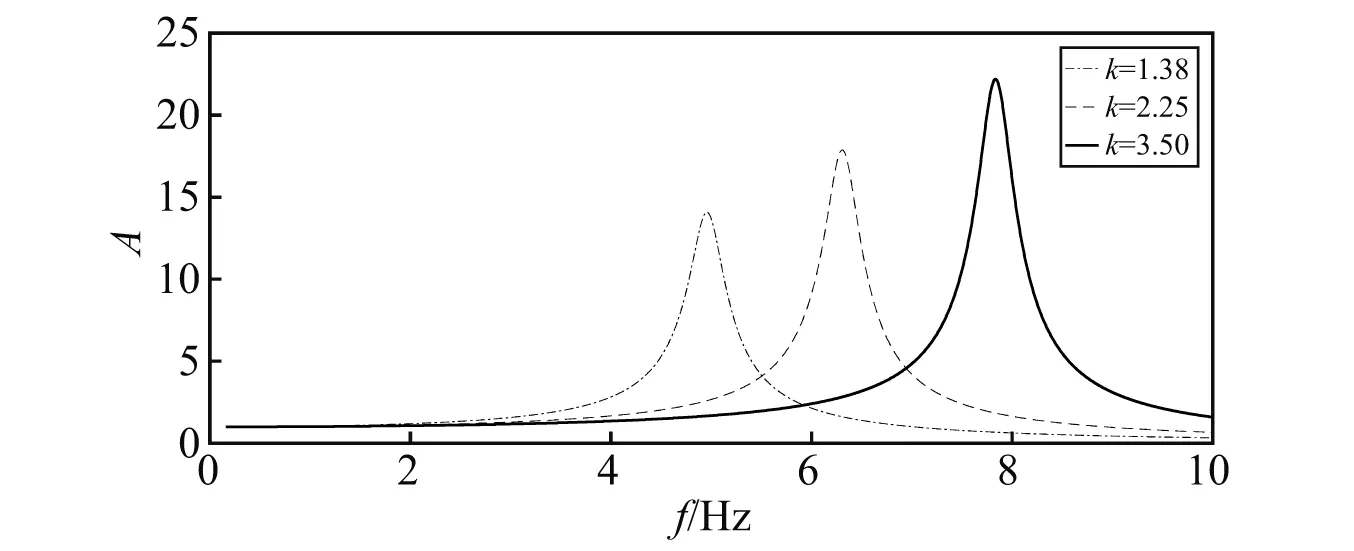
图11 横向弹簧无压紧力时理论计算曲线
图10与图11所示表明,在各向选用参数相同弹簧作为缓冲减振系统的情况下,两图所示趋势基本一致。其中各固有频率点所对应的加速度响应值存在一定的差异,主要为振动台的加速度稳定性较差所致。当选用弹簧刚度越大,系统的固有频率随之增加,且振动响应幅值在共振点处明显提高,具体修正模型计算结果与试验所得固有频率值见表5。
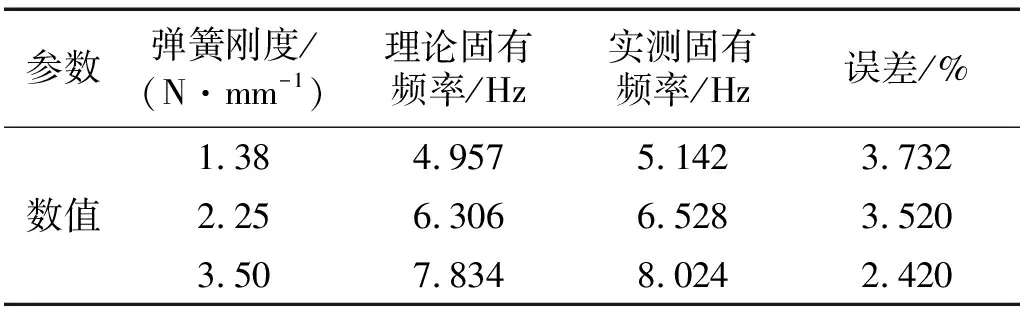
表5 固有频率及误差
对固有频率的理论计算值与试验实测值进行比较,结果显示两类数值接近。误差最大值仅为3.732%。由于振动台自身存在2.34%的输出频率误差,各自实测固有频率值还可再分别降低2.34%,理论结果与试验测试结果将更为接近,这表明:本文所提出的考虑横向弹簧径向刚度的精密包装缓冲系统振动特性修正模型具有较好的可行性。
实际缓冲包装系统中横向与纵向弹簧可能存在差异,令横向弹簧刚度为k1,纵向弹簧刚度为k2,试验分析k2在1.38 N/mm,2.25 N/mm以及3.5 N/mm时横向弹簧刚度对纵向固有频率的影响。测试结果曲线如图12所示。

图12 不同横向弹簧刚度下试验曲线
由图12测试结果可知:纵向固有频率总会随着横向弹簧刚度k1的变化而变化。针对本试验结构,当纵向弹簧刚度k2一定时,横向弹簧刚度k1不会改变纵向固有频率的曲线形态。在纵向弹簧刚度k2相同的情况下,随着横向弹簧刚度k1的增大,纵向固有频率的峰值点逐渐后移,其最大值也会逐渐变大。
当横向弹簧有一定预压紧力时,横向弹簧对物块的作用力较大,采用三种不同的横向刚度弹簧进行测试。测试结果如图13所示。
由图13可知:当弹簧刚度为2.25 N/mm且横向弹簧存在压缩时,压缩长度增大,系统固有频率也会随之增加,分别是6.579 Hz,6.692 Hz和6.788 Hz,且加速度响应峰值略有增加,这与理论分析得到的规律一致。当弹簧刚度分别为1.38 N/mm和3.5 N/mm时,其试验结果的规律与之类似。这说明在压缩工况下,固有频率会随着横向弹簧压缩量的增加而增加。可见,横向缓冲系统的刚度对于精密包装缓冲系统纵向振动的影响具有一定的规律性。
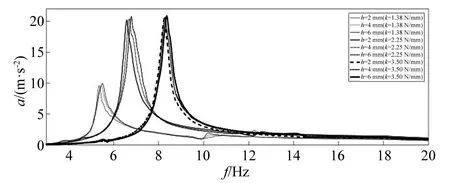
图13 不同压缩量时三种横向弹簧刚度时加速度试验曲线
对比横向无弹簧与横向有弹簧以及不同横向弹簧刚度作用等工况下的测试结果,如图14所示。由图可知:当纵向弹簧刚度k2一定时,安装横向弹簧后,缓冲包装系统纵向固有频率对应加速度峰值点增大。当增加横向弹簧刚度k1后,缓冲包装系统纵向固有频率峰值点也随之增大。
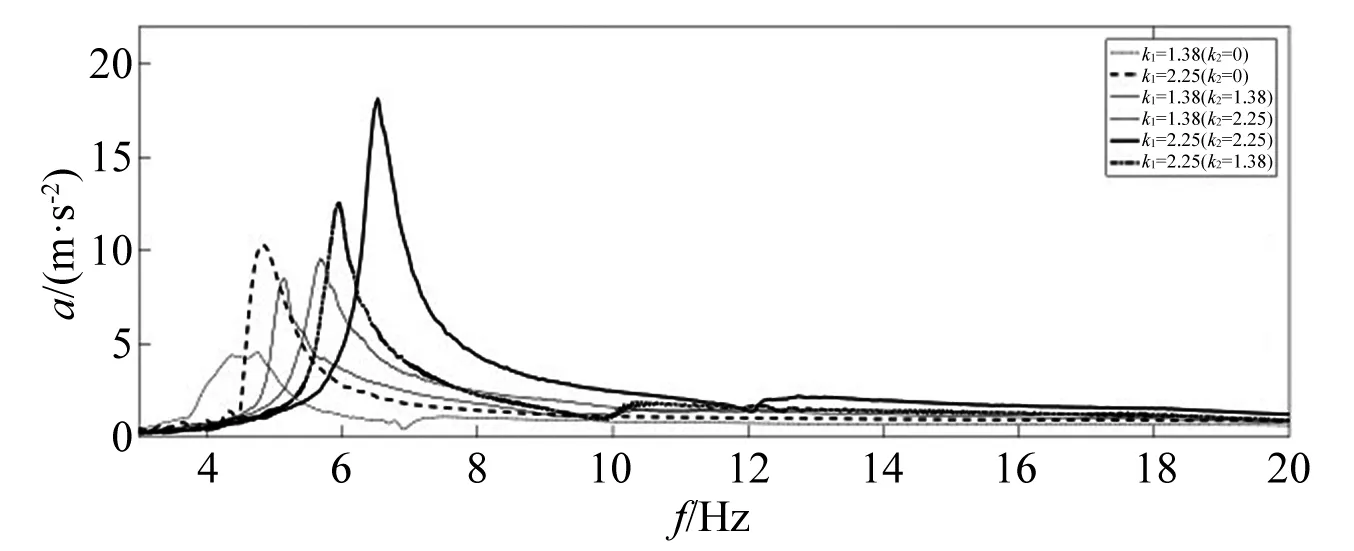
图14 横向有无弹簧及横向弹簧刚度不同的试验曲线
随着缓冲包装系统固有频率的增加,弹簧刚度为k2=1.38 N/mm,k1=0(即无横向弹簧)与k2=1.38 N/mm,k1=1.38 N/mm时,相同固有频率下所对应的加速度比大于1并逐渐增大;当频率为4.168 32 Hz时,两工况下纵向加速度值比出现峰值并逐渐减小,此过程中横向弹簧有利于提高精密包装弹性支撑缓冲系统的减振效果。当频率增加到5.243 86 Hz时,两工况下纵向加速度比小于1并逐渐减少,后逐渐趋于稳定,即当固有频率增加到5.243 86 Hz时,横向弹簧对精密包装弹性支撑缓冲系统的减振效果影响较小。同理,当弹簧刚度为k2=1.38 N/mm,k1=0(即无横向弹簧)与k2=1.38 N/mm,k1=2.25 N/mm时纵向加速度比峰值出现在4.306 22 Hz,增加到5.435 93 Hz时加速度比小于1并逐渐减少。弹簧刚度为k2=2.25 N/mm,k1=0(即无横向弹簧)与k2=2.25 N/mm,k1=1.38时,纵向加速度比峰值出现在4.805 18 Hz,增加到5.780 58 Hz时加速度比小于1并逐渐减小。当弹簧刚度为k2=2.25 N/mm,k1=0和k2=2.25 N/mm,k1=2.25 N/mm时,加速度比峰值出现在4.821 67 Hz,增加到5.952 56 Hz时加速度比小于1并逐渐减小。由此可见,精密包装弹性支撑缓冲系统在特定固有频率范围内(本试验例中其值均小于6 Hz)振动,在纵向弹簧的基础上安装横向弹簧,对包装件缓冲性能的提高有明显作用。
4 结 论
通过引入弹簧径向刚度对包装缓冲系统振动特性进行理论与试验研究,可以得到如下结论:
(1)当横向弹簧轴向预压紧时,随着压紧力的增大,包装缓冲系统固有频率及加速度响应峰值也会随之增加。运输中遭受高频激励时,可降低包装缓冲系统两侧预紧力,遭受低频激励时,可提高包装缓冲系统两侧预紧力,从而避免共振现象的发生,保护包装内部产品。
(2)径向刚度系数越大,包装缓冲系统共振幅值响应越大。为避免共振,应适当降低包装缓冲系统的固有频率,且应充分考虑横向弹簧对其振动特性的影响。
(3)工况二时缓冲包装系统在X,Z向的加速度峰值更小。相较于工况一,其加速度的变化差值更小。在初位移状态下,因加速度变化过大导致的产品损坏的几率在一定程度上低于工况一时的振动系统。为平衡产品的各向加速度响应,不应无限制的增加或减少单一支承点的减振器刚度,否则会对其他方向产生不利影响。
(4)试验结果表明:纵向固有频率总会随着横向弹簧刚度的变化而变化。在各向选用相同参数弹簧减振的情况下,系统的固有频率变化趋势基本一致。在纵向弹簧刚度相同的情况下,当横向弹簧刚度越大,系统的固有频率越大,且振动响应幅值在共振点处明显提高,其峰值点也随之明显后移,这与理论相一致。
