电磁直线式主动悬架作动器参数的多目标粒子群优化

2021-12-02寇发荣李阳康

振动与冲击 2021年22期

寇发荣，张宏，李阳康，洪锋

(西安科技大学机械工程学院，西安 710054)

随着汽车性能的提升，传统的被动悬架无法满足现代车辆对平顺性和操纵稳定性的需求，而电磁主动悬架具有在满足操作稳定性和行驶平顺性的要求之外，相比其他类型的主动悬架还具有安全可靠性高、较少的机械部件、系统配置更加的简单灵活，同时其密封性要求低等优点，使其成为该研究领域的热点问题[1-4]。

邓兆祥等[5]设计了一种新型电磁直线感应式作动器，并系统分析了作动器结构参数和电气参数对电磁力大小和响应速度的影响规律。杨超等[6]提出了一种外壳结构采用圆筒形状的直线电机式电磁作动器，设计出12槽14极电磁直线电机，并通过有限元分析和理论计算相结合的方法，检验了模型的正确性。王明杰等[7]提出了一种永磁直线同步电机精确子域模型，通过建立精确的数学模型，解决齿槽效应对永磁直线同步电机复杂气隙磁场的影响，进一步完善了传统永磁直线同步电机理论。Han等[8]提出了一种新型电磁直线电机，研究了磁簧、电机力、谐振频率和总体性能。利用有限元分析方法，对电磁作动器的各种励磁电流和电枢位置进行了静态力建模，搭建了试验台架，对电机力进行了测量，试验验证了模型的正确性。但上述研究中，还没有通过对电磁作动器的设计参数直接进行优化来改进其性能。

本研究针对电磁直线式主动悬架作动器电磁波动力大、有效输出力低的问题，分别对作动器槽口宽度、初级边端长度和极距长度进行多目标粒子群算法参数优化，并对优化前后作动器性能进行对比分析。试制了作动器物理样机，通过特性试验验证有限元仿真的有效性，为以后整车装备提供了一定理论数据。

1 电磁主动悬架的结构设计

轮毂电机驱动的电动汽车电磁作动器安装示意图，如图1所示。该作动器采用长次级短初级结构，次级在绕组线圈的作用下做直线运动。初级线圈在三相交流电流的作用下，作动器内部产生沿作动器轴向方向波动的正弦行波磁场，而次级铁芯在行波磁场的作用下产生沿轴向方向的电磁推力，若定子固定不动，则动子在电磁推力的作用下，沿着轴向的方向产生相对往复运动，中间不需要任何换向装置。在悬架控制器的作用下，电磁作动器输出主动力抑制车身的振动，进而提高汽车的平稳性。

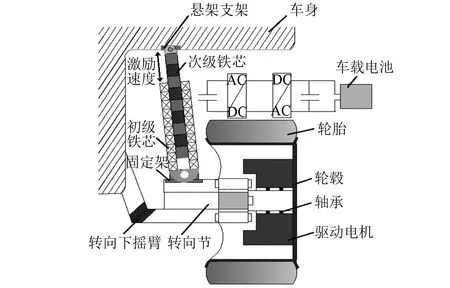
图1 轮毂电机驱动的电动汽车电磁直线作动器安装示意图

本设计中，采用旋转电机的匹配方法，并结合底盘安装空间的要求，选择作动器的槽数为12，槽宽长度为12 mm，初级槽型选为平底结构。为了减小作动器的体积，提高有效磁密强度，本文选择分数槽结构。当分数槽为12时，为了减小绕组线圈的电磁推力的波动和提高作动器输出稳定性[9]，提高作动器有效输出力，提高作动器的寿命，作动器选择极对数选择5[10]。作动器的结构参数如表1所示。

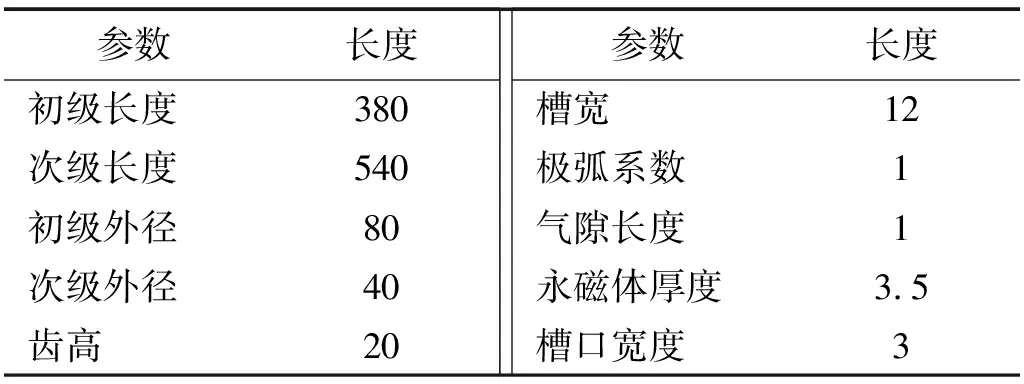
表1 作动器的主要结构参数

2 电磁作动器有限元模型建立与验证

2.1 电磁有限元模型的建立

根据表1作动器主要结构尺寸参数，利用电磁有限元仿真软件对作动器进行二维模型的搭建，模型如图2所示。

图2 电磁直线作动器有限元模型

为了减小有限元分析过程的误差，提高仿真求解的精度，对求解区域的网格划分应该较密。作动器网格划分后的结果，如图3所示。

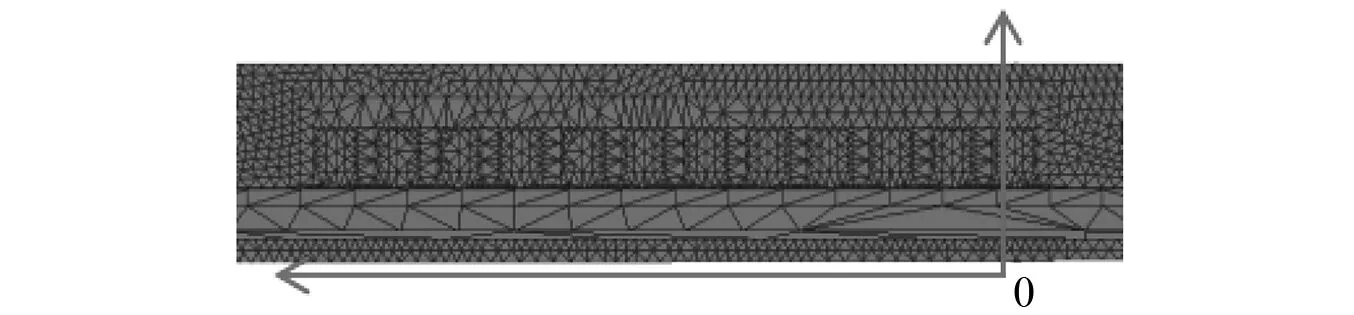
图3 电磁直线作动器网格划分

2.2 作动器模型的验证

基于标量磁位分离法[11]，假设磁体表面为等磁位面，并设定外壳定子磁位为零，则在电磁直线作动器的动子外表面处，一对磁极的磁动势F(z)分布为

(1)

式中：z为轴向长度，对于永磁体；F0=Br/μrr4，剩磁Br=1.1 T，相对磁导率ur=1.04，r4为永磁体厚度；τ0为永磁体长度。

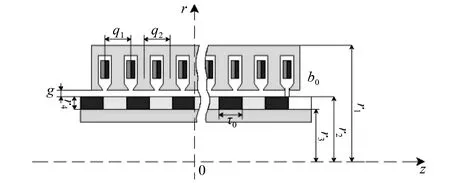
图4 作动器的结构尺寸示意图

将气隙磁位展开傅里叶级数

(2)

式中：z为轴向长度；τ为极距，作动器极弧系数αp(定义τ/τ0=1)，故τ=τ0。

作动器标量磁位满足拉普拉斯方程

(3)

气隙磁场定解的边界条件为

(4)

采用分离变量法，可变形为

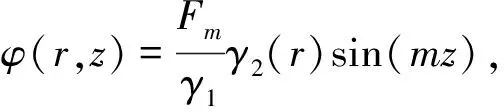
γ1=I0(mr1)K0(mr2)-I0(mr2)K0(mr1),

γ2=I0(mr1)K0(mr)-I0(mr)K0(mr1)

(5)

式中：I0(·)为第1类0阶变形贝塞尔函数；K0(·)为第2类0阶变形贝塞尔函数。

根据Br(r,z)=-u0dφ(r,z)/dr，u0为真空磁导率，u0=4π×10-7N/A2，可推导出径向磁通密度Br(r,z)理论计算为

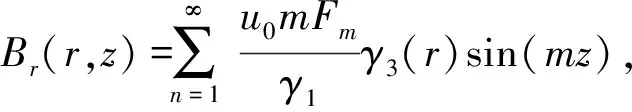
γ3=I0(mr1)K1(mr)+I1(mr)K0(mr1)

(6)

式中：I1(·)为第1类1阶变形贝塞尔函数；K1(·)为第2类1阶变形贝塞尔函数。

作动器的卡特尔系数Kc

(7)

其中，

g′=g+r4/ur,

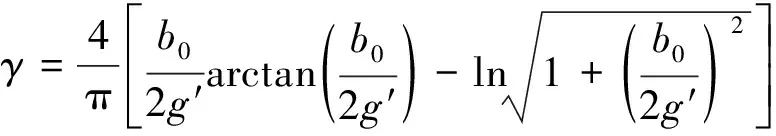
式中：q1和γ分别为作动器的槽距和开槽系数；g为气隙厚度。

作动器的有效气隙ge为

ge=g+(Kc-1)g′

(8)

式中,Re为等效电枢半径，Re=r2+ge。

可以推导出径向磁密强度Bar(z)为

Bar(z)|r=Re=Br(Re,z)

(9)

式中：Bar和ge分别为作动器的有效气隙和径向磁通密度。

空载时，在作动器加载电压等于0，作动器次级运行速度等于1.5 m/s的条件下，分析一周期内作动器的径向磁密强度大小，并与理论计算值对比。径向磁密强度随次级位移的变化，如图5所示。

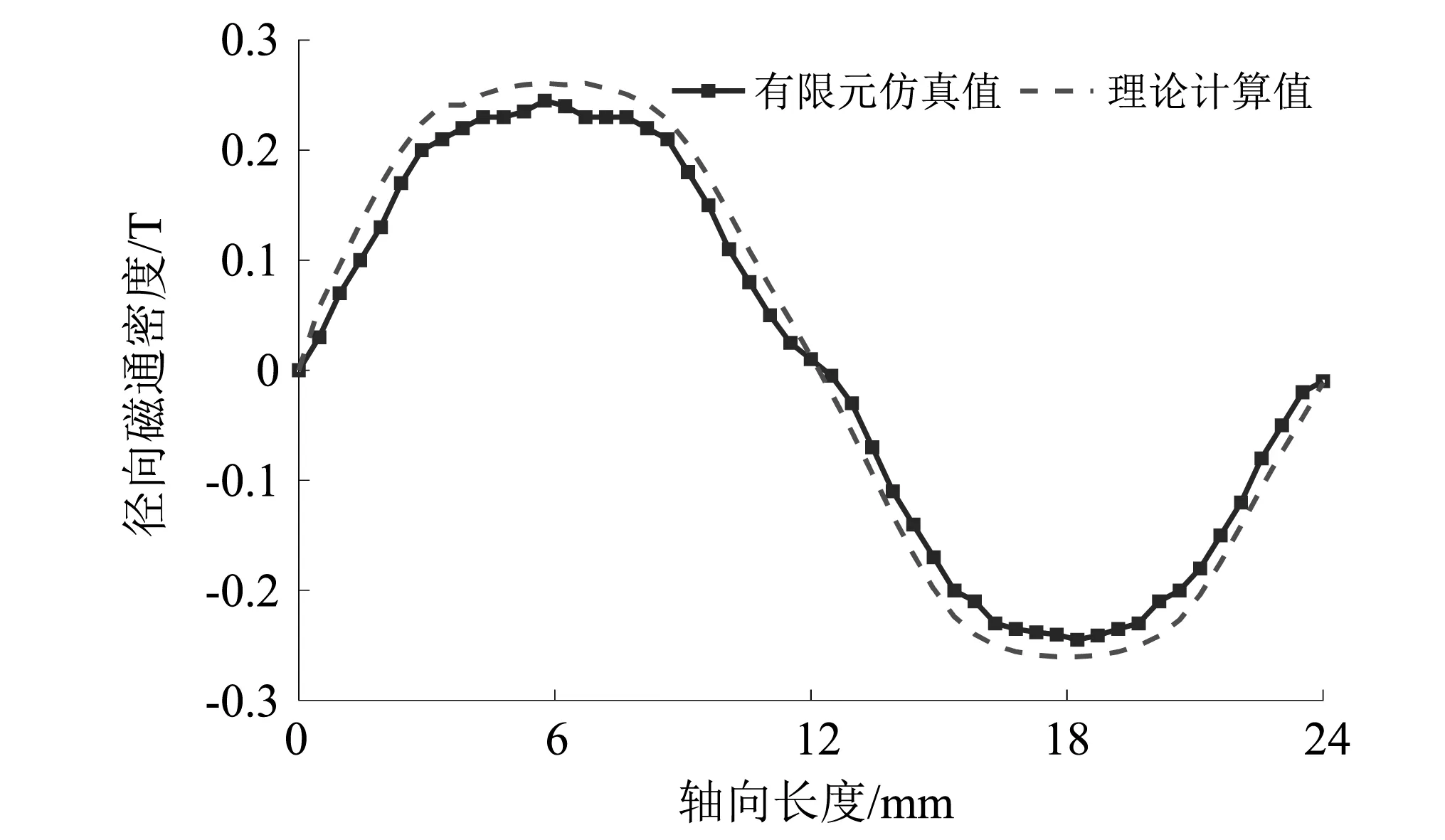
图5 作动器径向磁通密度随次级运动位移的变化

由图5可知，在一个周期内径向气隙磁通密度有限元分析值和理论计算值吻合良好，从而验证了模型的可行性。虽然理论计算值大于有限元分析值，主要是因为有限元分析过程中气隙中存在谐波成分，而理论计算值将其假设为理想的正弦波。

3 作动器参数优化

3.1 电磁直线作动器电磁力分析

作动器电磁推力并不是一个理想的稳定数值。这种波动造成了悬架系统振动和噪声变大，对车身的控制和减振有很大的影响，而这种波动和噪声主要由齿槽力和边端力组成的。

考虑电磁力波动的主动悬架动力学模型，如图6所示。系统仿真原理是在LQG主动控制器求出悬架系统需求的理想控制力，再求出不含波动力的作动器输入电流，结合作动器的运行状态，得出包含波动力的作动器实际输出力，最后使实际输出力与理想电磁力作对比分析。

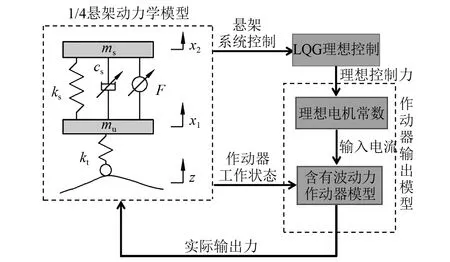
图6 车辆1/4主动悬架系统

根据悬架系统的仿真模型及主动悬架控制器参数，路面激励为B级路面，车速等于80 km/h，仿真时间为10 s，结果如图7和图8所示。

图7 作动器实际电磁力和理想输出力

图8 作动器理想输出力与实际输出力差值

由图7和图8可以得出，与LQG得到的理想输出力相比，电磁直线主动悬架的实际控制力波动较大，最大达到21.3 N，由于输入电流的限制，实际控制力在一段区间内的最大值和均方根值都有一定程度的降低。

3.2 电磁直线作动器波动力分析

3.2.1 作动器边端力

由于电磁作动器两端的突变，是造成作动器边端效应的主要原因。对于任意边端长度的电磁作动器，左右边端力分别为F+和F-。所以总的端部力的合力可表示为

(10)

其中，

式中：τ为极距；Fsk和Fck为第阶傅里叶分解系数；σ为电机初级长度。

3.2.2 作动器齿槽力

为了提高作动器工作稳定性和精度，可以采用优化槽口宽度的方法，提高气隙磁场的正弦度，减小感应电动势的谐波含量。

在计算过程中作以下等效替换：①作动器内部不存在涡流现象；②作动器的初级齿为矩形；③气隙磁场的波形随时间的变化为方波；④永磁体磁导率与空气相同。

在忽略初级铁芯磁饱和前提下，根据能量守恒定律，可以得到作动器总磁场能量W近似等于气隙磁场的能量Wgap，齿槽力为

(11)

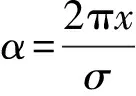
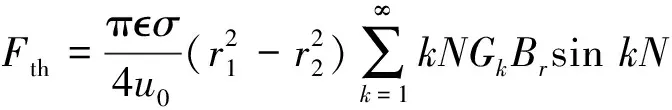
k=1,2,3,…

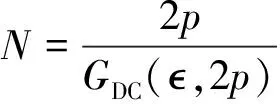
(12)

式中：Br和Gk分别为永磁体产生气隙磁密平方的傅里叶分解系数和相对气隙磁导平方的傅里叶分解系数[12]；p，和GDC分别为电磁作动器的极对数、作动器的槽数和最大公约数。

(13)

因此选择适当的槽口宽度b0，可以使Gk减小甚至接近等于0，以达到提高作动器稳定性目的，即

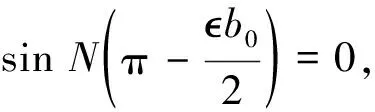
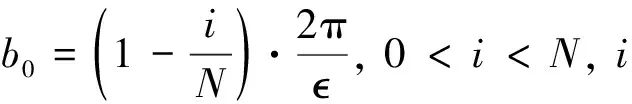
(14)

3.3 电磁直线作动器参数敏感度分析

3.3.1 作动器齿槽开口

在作动器加载峰值电压为50 V三相交流电，作动器次级速度设定为0.13 m/s的匀速运动条件下，分别搭建不同槽口宽度的有限元模型。平均电磁力和波动比随齿槽开口的波动曲线结果，如图9所示。

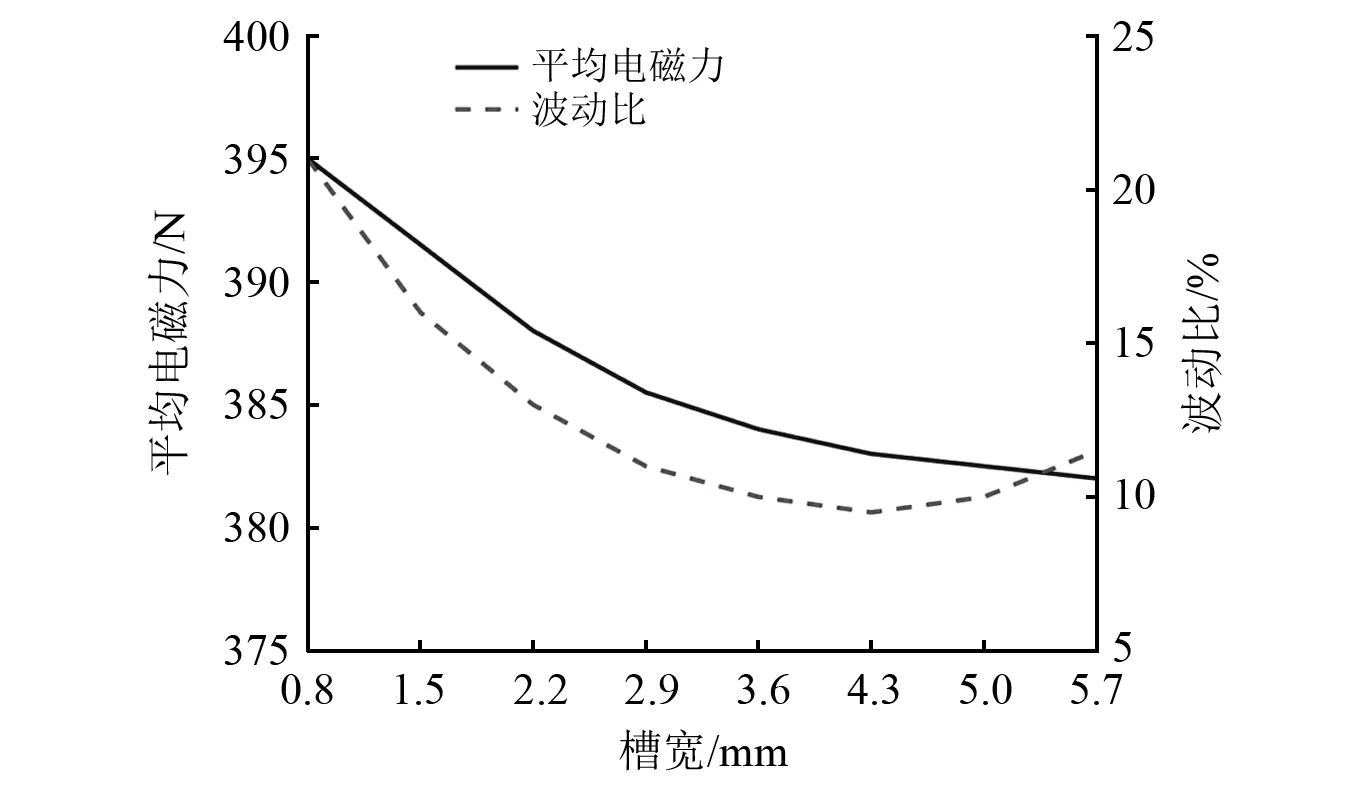
图9 平均电磁力和波动比随齿槽开口的变化

由图9可得，当槽宽为4.3 mm，平均电磁力为384.3 N，作动器的最小波动比为9.5%，最小推力波动为36.5 N，在平均电磁力牺牲较小的情况下，作动器的稳定性明显提高。但槽口宽度与理论计算存在一定的区别，主要理论计算忽略了涡流和磁滞损耗以及将气隙磁场假设为方波的原因。

在实际工作中，线圈绕组的感应电动势含有谐波成分，在感应电流作用下产生波动力。由于输入电压是理想的正弦波，因此只分析感应电动势的谐波。谐波与基波之比是评定谐波分量大小，计算公式为

(15)

式中：η为谐波与基波之比；G1和Gn分别为基波分量的有效值和第n次谐波分量的有效值。

感应电动势的谐波分量，如图10所示。除了感应电动势的基波外，谐波主要存在于第3次、第2次、第4次、第5次和第6次，其中3次谐波占基波的比例最大，6次谐波占基波的比例最小，因此式(15)中n=6。

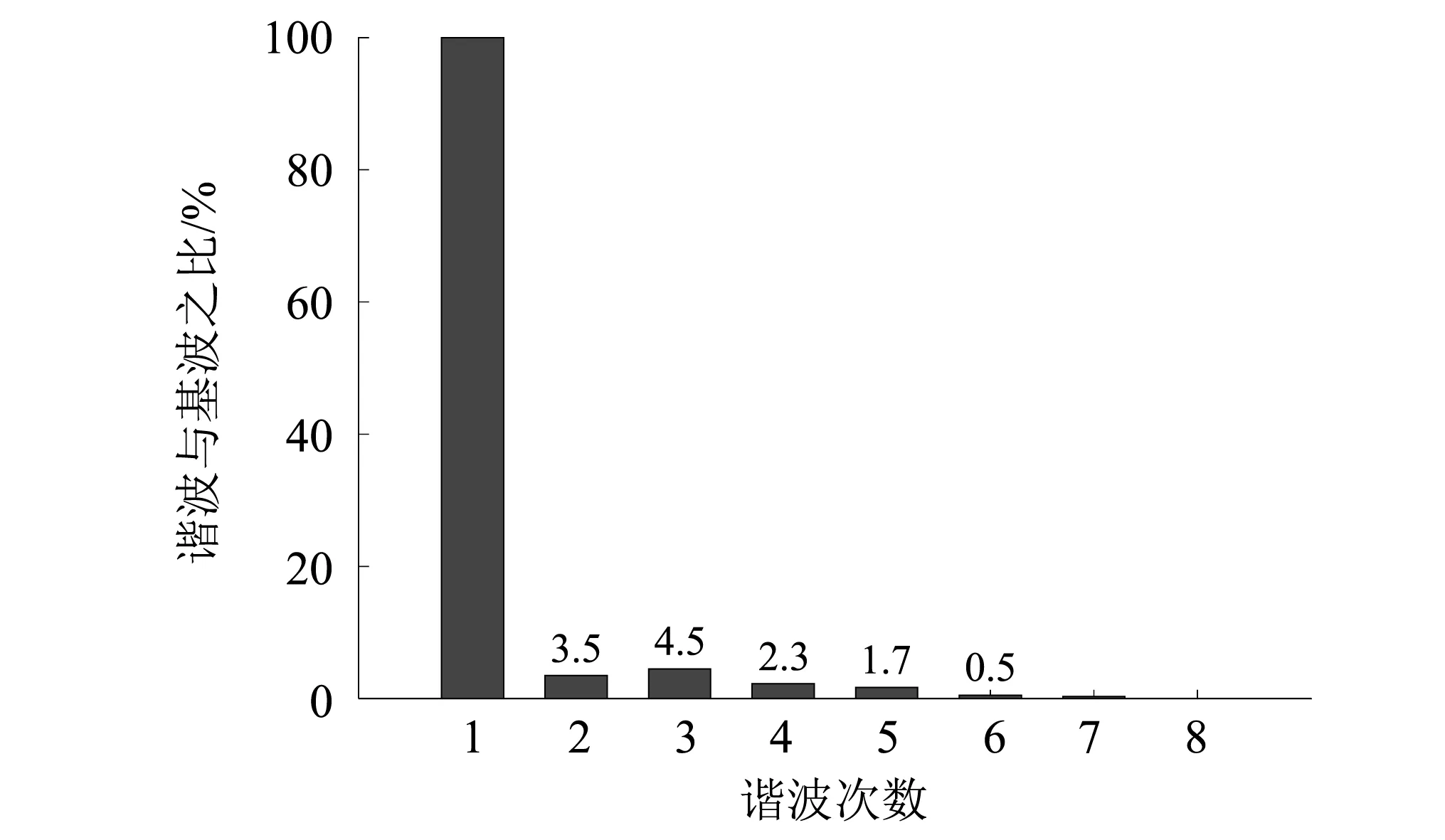
图10 感应电动势的谐波分量

利用谐波畸变率评价不同槽宽下感应电动势波形的影响。计算过程为

(16)

式中：RTHD为总谐波畸变率；H=6。

根据槽宽的理论计算结果，改变槽宽得到不同的总谐波畸变率，总谐波畸变率随槽宽的变化结果，如图11所示。

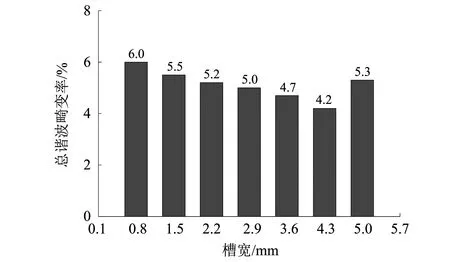
图11 总谐波畸变率随槽宽的变化

由图11可知，当槽口宽为4.3 mm时，总谐波畸变率最小，与理论计算结果基本一致。因此，在槽口宽为4.3 mm时，可以有效地减小齿槽力，提高作动器的稳定性。

3.3.2 作动器初级边端长度

在作动器加载峰值电压为50 V三相交流电，作动器次级速度设定为0.13 m/s的匀速运动条件下，建立不同边端长度的有限元模型。波动曲线结果如图12所示。

图12 平均电磁力和波动比随初级长度的变化

由图12可得，当边端长度为4 mm，作动器的平均电磁力为234.1 N，最小波动比为9.43%，最小推力波动为22.06 N，作动器的平均电磁推力有所减小，但是作动器的稳定性明显提高。

根据式(16)分析边端长度对总谐波畸变率的影响，分析结果如图13所示。

由图13可知，总谐波畸变率随边端长度的增加先减小后增大。当初级边端长度为4 mm时，总谐波畸变率最小。

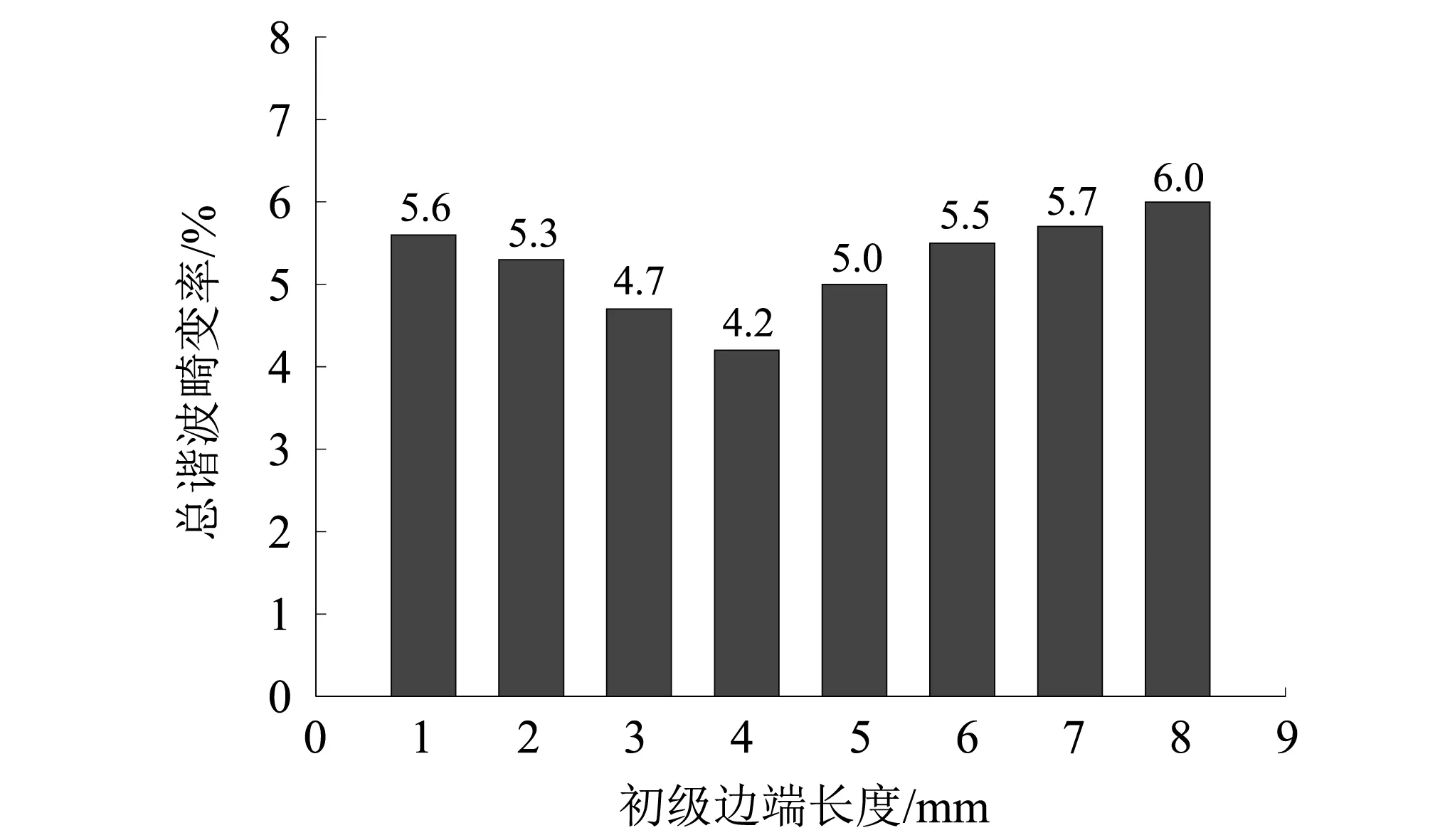
图13 总谐波畸变率随初级边端长度的变化

3.3.3 作动器极距长度

选择合适的极距可以有效减弱电磁作动器的边端力。建立不同极距长度的有限元模型，曲线变化结果如图14所示。

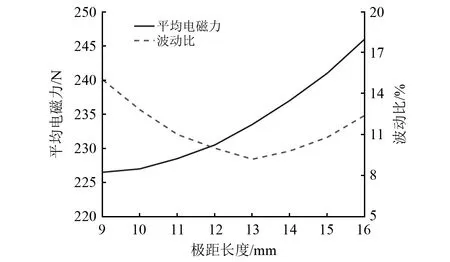
图14 平均电磁力和波动比随极距长度的变化

由图14可知，当作动器的极距长度等于11 mm时，电磁波动比最小。此时平均电磁推力等于234.5 N，波动比为9.5%，在较小牺牲电磁力同时，可以有效提高作动器的输出精度。

根据式(16)分析在不同极距长度下作动器的总谐波畸变率，仿真结果如图15所示。

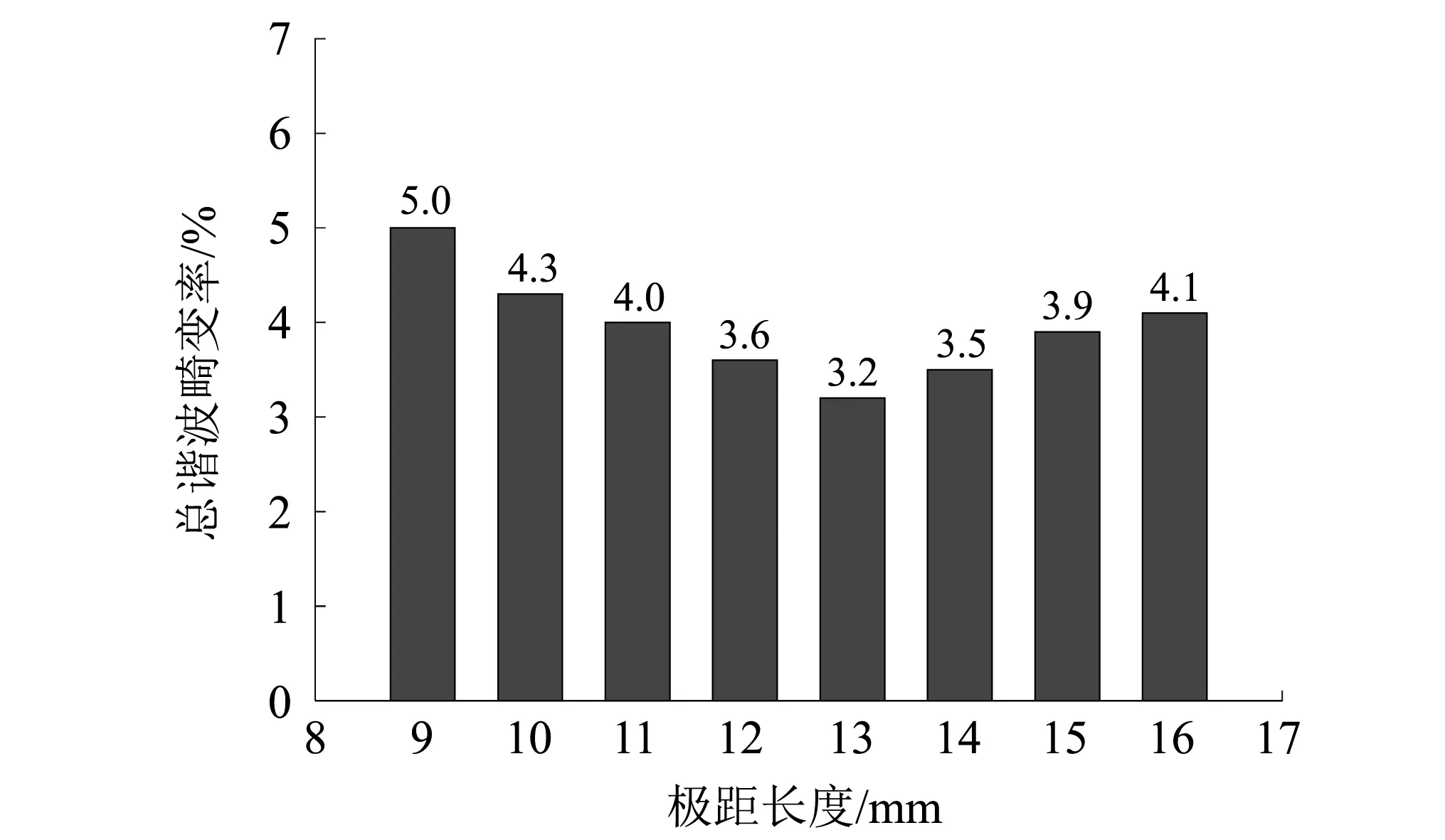
图15 总谐波畸变率随极距长度变化

由图15可知，在负载条件下，随着极距长度的增加，总谐波畸变率先减小后增加。在极距长度等于13 mm时，总谐波畸变率最小为3.2%。

3.4 作动器参数的多目标粒子群优化

3.4.1 优化目标

提高作动器的稳定性，主要目标是减小作动器的电磁力波动值。从作动器的结构参数敏感性分析可得，作动器电磁推力和波动比主要与槽口宽度、初级长度、极距长度有关，而且三者之间相互影响。

电磁推力大小和感应电动势谐波含量分别采用输出力Ft和总谐波畸变率RTHD作为评价标准。对作动器结构参数的优化，一方面需要降低电动势中谐波含量，以降低作动器电磁推力的波动；另外一方面要提高电动势的峰值，进而提高有效输出推力。因此设计目标维数n=2，选取设计目标函数如下：

目标函数1

f1(x)=Ft

(17)

目标函数2

f2(x)=RTHD

(18)

为了满足作动器大电磁力输出，同时降低电磁力中的波动，在优化过程中采用大Ft、小RTHD方式，对优化算法的目标参数值进行筛选。

3.4.2 设计约束及变量

电磁作动器优化可以等效看作成由优化目标和约束条件组成的非线性数学问题，则多目标参数优化问题描述

Ffitness(x)=best{f1(x),f2(x),…,fn(x)}x∈T

(19)

T={x∈Rm,G:gimin≤gi(x)≤gimax,i=1,…,u}

(20)

式中：f1(x),f2(x),…,fn(x)分别为第1～n个优化设计目标；T为约束条件，Rm为设计变量域；G为变量约束；n为设计目标维数；m为设计变量维数，u为约束个数。

选取槽口宽度b0、初级边端长度L0和极距长度τ为设计变量，由初级和次级无接触运动、避免齿部强度和铁芯磁极饱和为要求，根据参数敏感度分析，确定变量b0,L0,τ取值范围，设计变量及约束条件：设计变量x=[b0,L0,τ]，约束条件为b0∈[0.8,5.7],L0∈[1,8]，τ∈[9,16]。

由此可得，粒子群优化算法的设计变量维数m=3。

在理想条件下设计变量为连续值，但考虑到作动器的加工精度和试制条件，在优化过程中设计变量参数间隔0.1 m。

3.4.3 多目标粒子群优化算法

本文引用了多目标粒子群参数优化，通过优化作动器结构参数减小感应电动势中谐波含量，提高线圈绕组中感应电动势的峰值，进而提高作动器的有效输出力。在优化算法过程中，采用一种主要由可变乘法因子和违反约束乘法组成的自适应惩罚函数方法[13]。自适应惩罚函数公式为

(21)

式中，m和t分别为约束条件个数和迭代次数，自适应惩罚函数由惩罚程度和目标函数数量级决定。

3.4.4 优化结果分析

优化过程中，采用标准学习因子：C1=C2=2，线性权重系数为0.4～0.9，最大速度vmax确定与筛选空间关系式

vmax=λ|x|max

(22)

式中，λ为最大速度与位置限制的比例系数。优化算法设计作动器λ取0.1，种群规模选择50，经过200迭代运算，得到悬架作动器结构参数的Pareto最优解[14]，如图16所示。

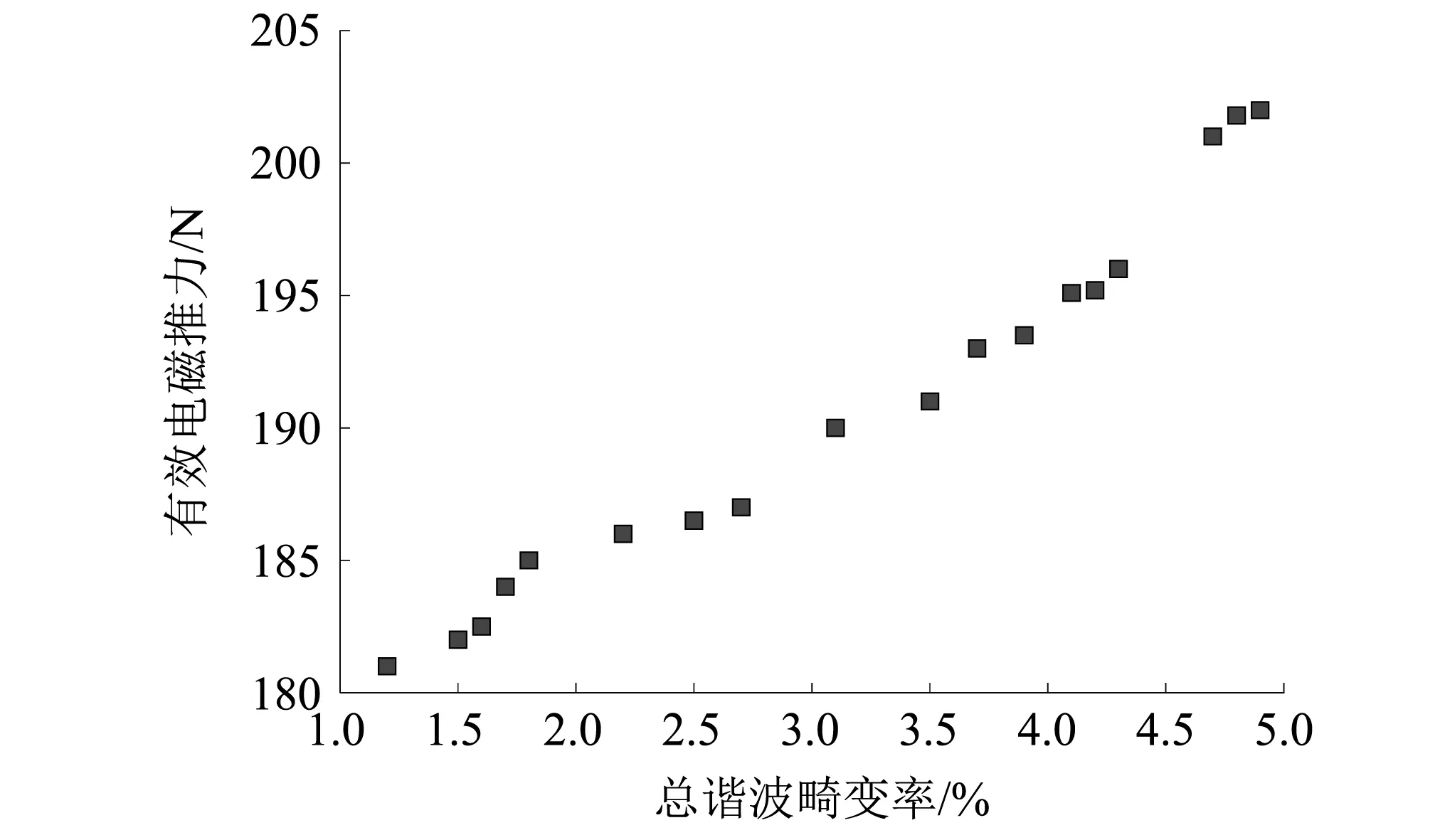
图16 Pareto最优解

由图16可知，最优解集包含了许多的非支配解，随着平均电磁力的增大，总谐波畸变率也随着增大，这种变化曲线互相矛盾，因此无法从最优解中筛选出符合参数要求的解集。

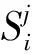
(23)

定义支配函数φk，第k个解的支配值为

(24)

式中：l为外部集中解的数目，根据模型的仿真结果，l取18；n为悬架优化设计目标个数，n=3。

将Pareto解集代入支配函数计算公式，可以得到每个非劣解的支配值，而支配值越大，说明该解集的综合性能最好，因此筛选出最大支配值的解作为优化结果的最优解。第6号粒子个体的支配值最大，综合性最强，如图17所示。优化前作动器参数值和6号粒子对应的最优解，如表2所示。

图17 Pareto最优解支配函数

表2 优化前后参数值的变化

根据表2对应的优化前后设计目标参数值，对作动器优化前后作动器的工作性能进行仿真分析。作动器加载电流为3 A条件下，优化前后电磁力随时间变化的对比曲线，如图18所示；作动器在空载情况下，次级速度为0.3 m/s，优化前后定位力随时间变化对比曲线，如图19所示；作动器空载条件下，次级运动速度为0.3 m/s，优化前后感应电动势随时间变化曲线，如图20所示；优化前后作动器性能参数对比，如表3所示。

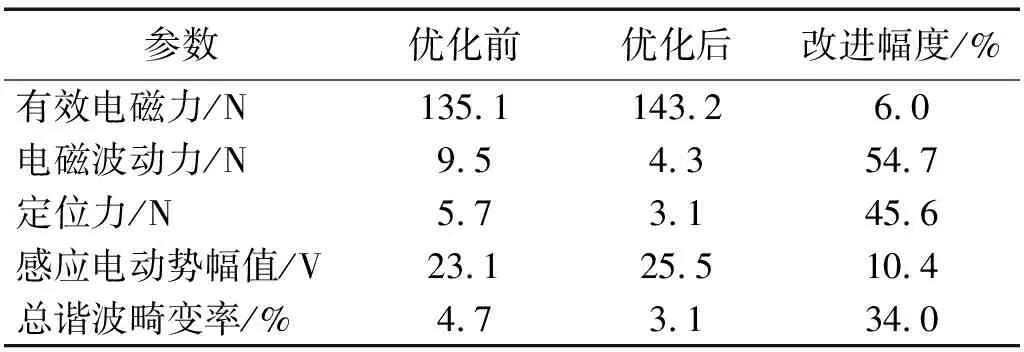
表3 优化前后作动器参数对比

由图18可以得出，优化后的作动器电磁推力随时间的变化上下峰值降低，有效电磁力也进一步变大。由图19可以得出，优化后作动器的定位力波动幅度降低，而且变化具有连贯性更加接近于0。由图20可以得出，在空载条件下，经过优化后感应电动势波形更加接近于正弦，波动的峰值也进一步提高。

图18 电磁力随时间变化的对比曲线图

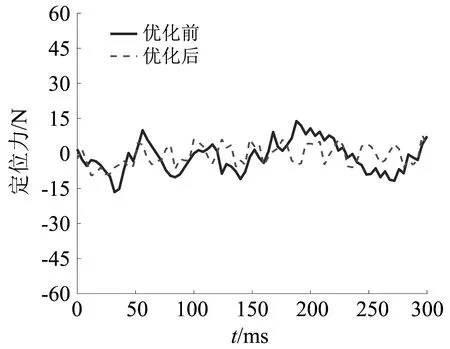
图19 定位力随时间变化的对比曲线

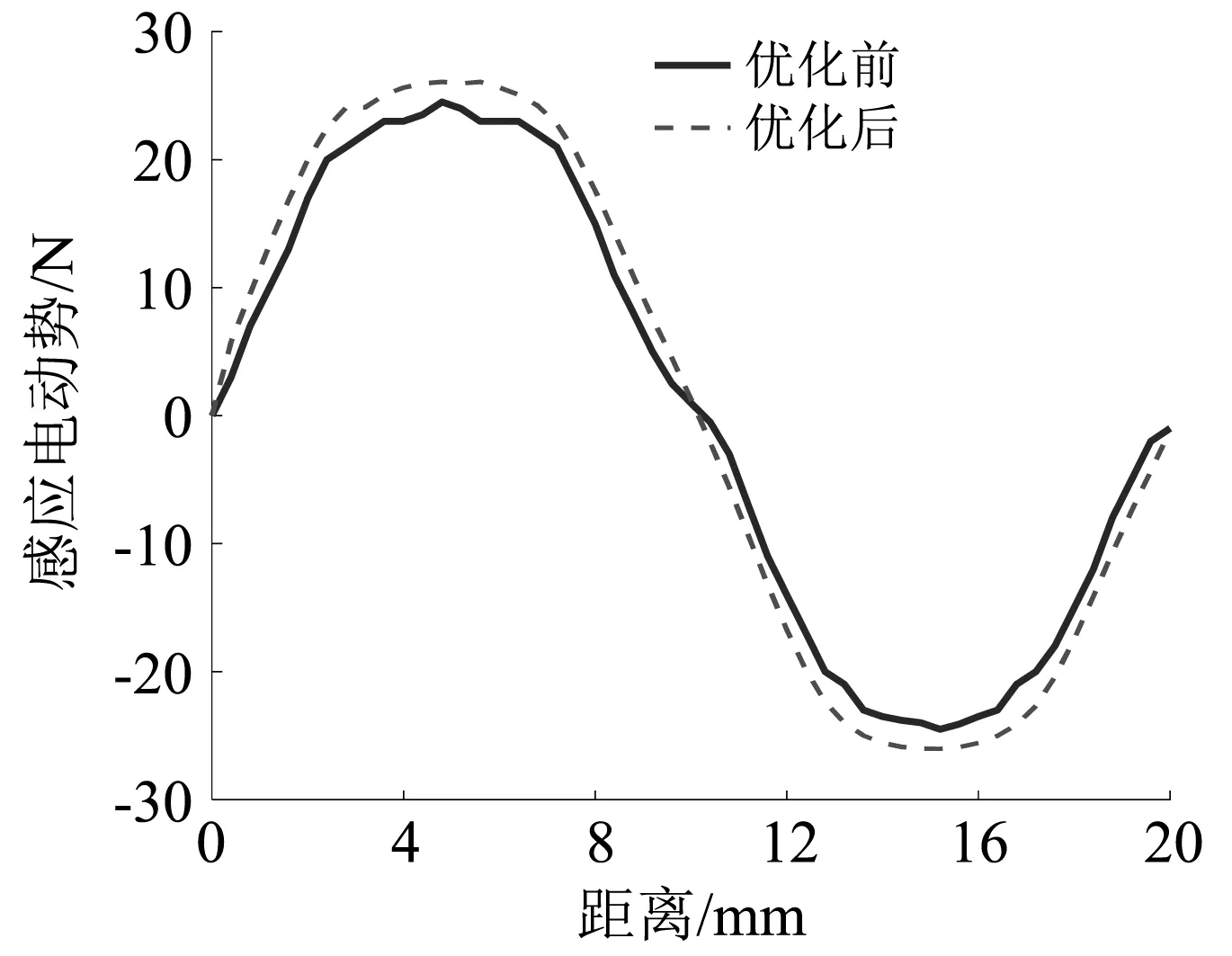
图20 感应电动势随距离变化的对比曲线

为了进一步分析作动器优化前后对悬架特性的影响，将优化后的结构参数代入主动悬架系统仿真模型中进行分析，优化前后电磁力输出对比曲线，如图21所示，可以得出优化后的实际电磁力出峰值相对优化前有明显的提升，而从图22可以得出实际电磁力的波动值也较优化前有了明显的降低。

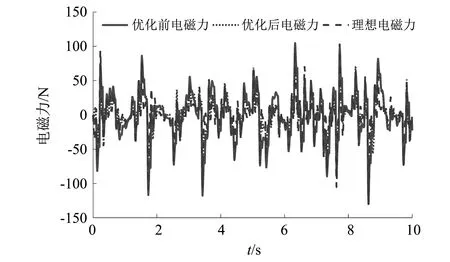
图21 作动器电磁力输出对比

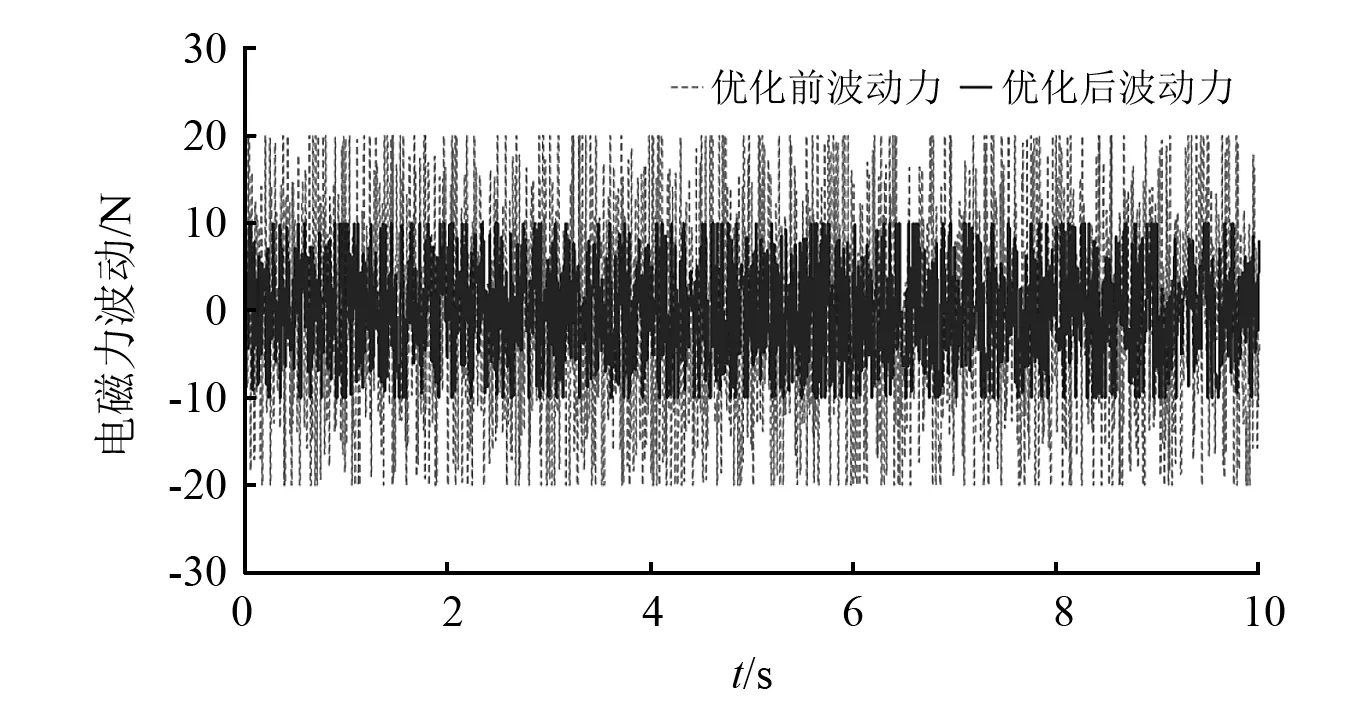
图22 电磁波动力对比

由图21和图22可以得出，实际电磁力输出均方根值与最大值分别上升4.5%与21.3%，电磁力波动均方根值与最大值分别下降51.7%与45.0%。

4 电磁直线作动器特性试验

4.1 作动器阻尼力特性

根据QC/T 545—1999汽车筒式减振器台架试验相关的规定和指导，开展对作动器的阻尼力特性试验。作动器测试设备主要包括WDTS-IV减振器综合电测示功机、电动激振台、上位机、作动器固定夹具、电磁悬架作动器、力传感器、位移传感器等。主要技术参数：激振力峰值为25 kN，激励最大速度为2 m/s，最大激振幅度为±70 mm。力传感器的测量范围为-10～10 kN。作动器阻尼力特性试验现场如图23所示。

图23 作动器阻尼力特性试验

在试验测试过程中，外部可调电阻设为2 Ω，分别以最大速度0.1 m/s，0.2 m/s，0.3 m/s和0.4 m/s，悬架行程为±10 mm下完成此次的测试任务，为了提高试验的精度，测试过程中作动器往复运动2次，取两次测试的平均值。为了得到相同加载条件下的阻尼力仿真值，通过Anosft软件建立了电机的外电路，其中绕组线圈的电感采用电感软件自动赋值，而电机的反向作用力代表阻尼力，如图24所示。

图24 不同速度下阻尼力随位移变化

作动器阻尼力波动值的仿真分析结果和测试结果，如表4所示。可以得出电磁直线作动器阻尼力波动仿真值与测试值相差约为3.6%～21.9%，两者之间相差较小，证明了阻尼力试验的有效性。

表4 阻尼力仿真波动值与试验值对比

4.2 作动器电磁力特性

在试验过程中，调节三相调压器旋钮，通过力传感器测得不同电压下输出力，取平均电磁力作为试验的有效值，并与有限元仿真值作对比分析，结果如图25所示。

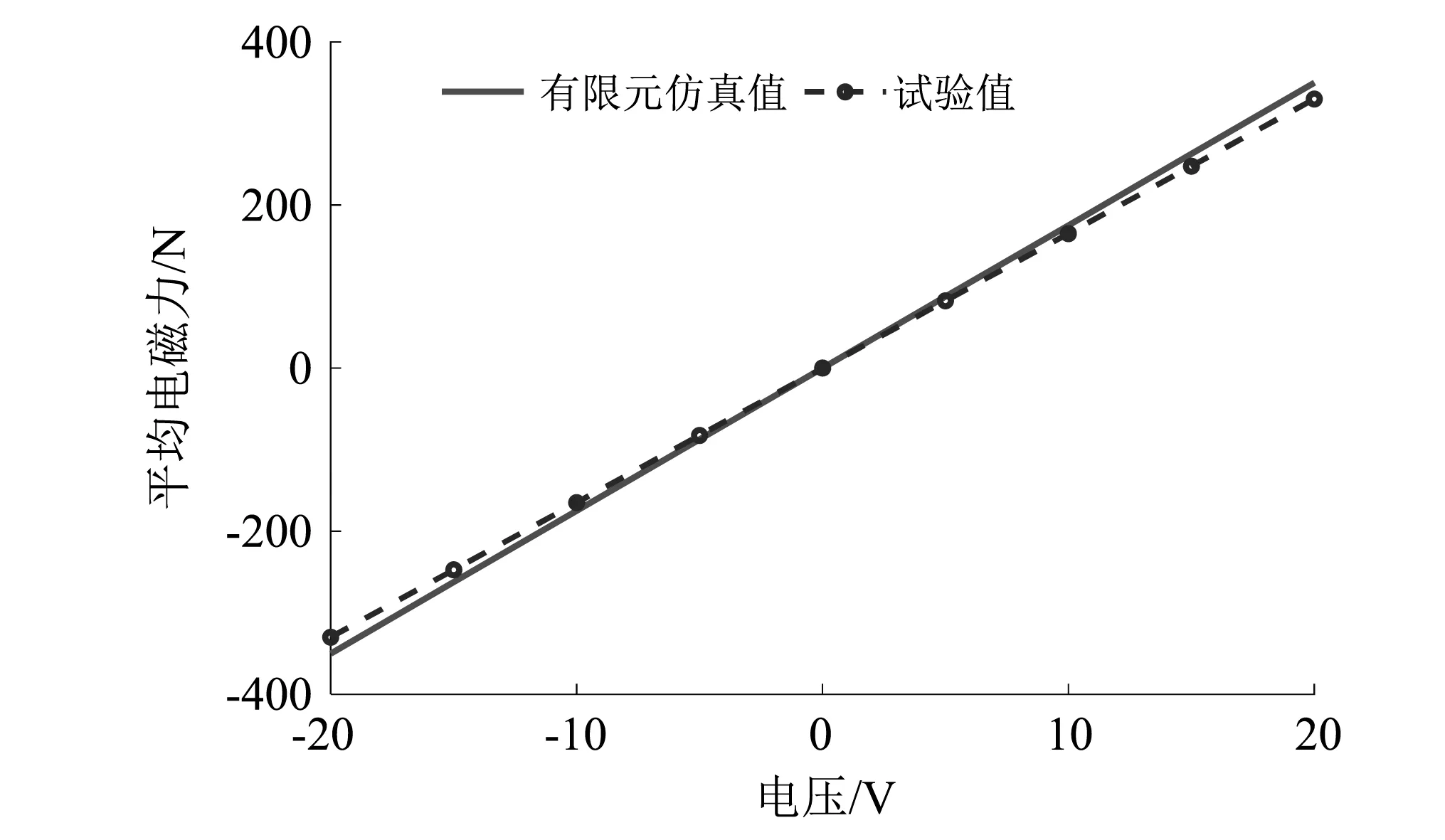
图25 平均电磁力随电压的变化

由图25可以得出，平均电磁力的试验值和有限元仿真值基本一致，且随时间的变化呈线性分布，两者之间误差值为4.2%～20.7%。当作动器外载输入电压为20 V，两者相差最大，此时平均电磁力试验值为181 N，有限元仿真值为150 N，主要由于有限元仿真将作动器简化为理想的模型，且不考虑机械能、铁损、铜损等能量的损耗。