空气舵系统摩擦模型及参数识别方法研究
2021-12-02李雨青南宫自军
李雨青,南宫自军,刘 博
(中国运载火箭技术研究院,北京 100076)
空气舵是飞行器广泛使用的执行机构,通过舵面偏转产生气动控制力,实现大气层内飞行姿态和轨迹控制的目的,是飞行控制系统中的关键环节[1]。空气舵系统是空气舵执行机构中的机械部分,一般由连杆、摇臂、舵轴、舵面等组成。空气舵系统不仅组成复杂,且存在不同类型的非线性因素,如摩擦、间隙等,使其动力学特性中的非线性问题尤为突出。在飞行过程中,如果这些非线性因素导致舵系统结构动力学特性超出了设计范围,将会影响飞行控制系统的稳定性能和舵翼结构的气动弹性特性,甚至造成飞行失利。因此,空气舵系统非线性建模及参数识别方法研究已成为了工程和学术界研究的热点。
在飞行器工程研制实践中,为解决间隙和摩擦非线性对舵系统传递特性的影响问题,首先需要对舵系统进行非线性建模。目前对于舵系统的非线性建模主要分为两类:一类是建立简化的数学模型;一类是建立基于接触碰撞力模型的多体动力学模型。王成华等[2]建立了舵系统含间隙及摩擦的单自由度数学模型;宿月文等[3]分别基于Hertz接触模型、K-V线性弹簧阻尼模型、L-N非线性弹簧模型,用拉格朗日方法建立含间隙约束副的多体系统动力学模型,从时域和频域对不同的摩擦接触模型下系统动态响应进行对比分析;李忠洪[4]将回转铰链碰撞动力学模型引入到传动机构分析中,建立了考虑间隙摩擦的空气舵传动机构的动力学方程,并构建了SIMULINK仿真模型。在舵系统建模中,如何对间隙和摩擦等非线性因素建模,是研究的关键问题。大量的专家学者对机械系统中的摩擦和间隙非线性因素模型开展了研究,文献[5-8]研究了各种不同的摩擦模型和间隙模型的特点及建模方法。然而,比较分析舵系统中摩擦非线性模型的研究较少,这直接影响了建模及动特性分析的准确性。为此,本文采用简化的单自由度模型,讨论某型空气舵系统的摩擦模型。
此外,对于获取非线性模型中的参数也是目前工程实践中面临的瓶颈难题,主要解决方法是模型参数的识别。大量的专家学者提出了不同的参数识别方法,如能量法[9]、频域法[10]、遗传算法[11]和等效线性化理论的各种方法等[12]。本文分别采用最小二乘非线性拟合法及遗传算法对所建模型中的参数进行识别,并分析了两种参数识别方法的效果。
1 空气舵系统非线性动力学
空气舵系统由舵面、舵轴、锥销、摇臂、连杆、铰链组成,如图1所示,其中在两铰链处存在间隙和干摩擦等非线性因素。
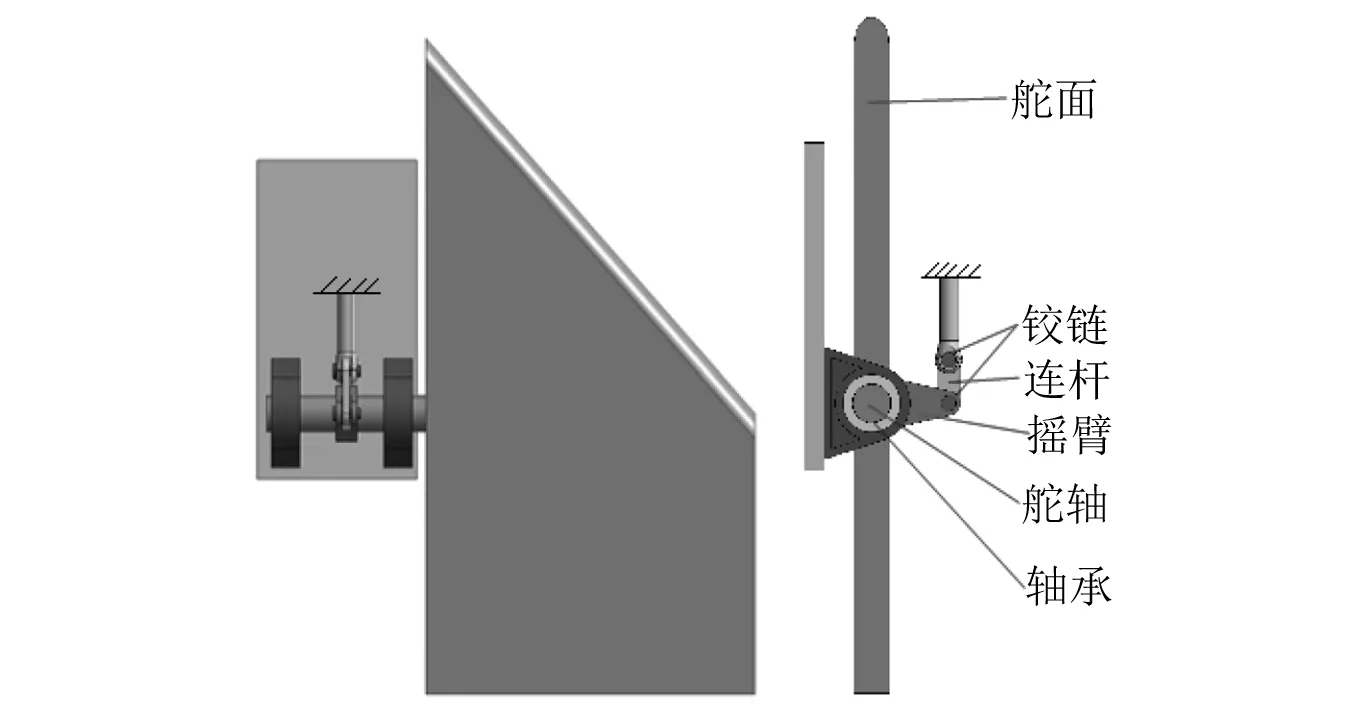
图1 空气舵传动环节示意图
含间隙和干摩擦的空气舵系统在激励力矩下的动力学模型可简化为单自由度非线性弹簧阻尼模型,如图2所示。舵系统的扭转刚度取决于舵系统的转动惯量Jr和舵轴的等效扭转刚度K。为保证有足够的强度和刚度特性,一般航天飞行器空气舵舵面本身刚度相对较大,相当于一个刚体,因此舵轴的扭转刚度和传动组件的刚度对舵面偏转过程中系统的刚度起决定性作用。在简化过程中,用Jr表示舵系统(含舵面和传动机构)的转动惯量,用舵轴等效扭转刚度K表示舵轴的扭转刚度和曲柄连杆组件的刚度的串联刚度。舵系统的阻尼主要包括两部分:一部分是轴承游隙和舵系统结构本身的阻尼,可当作黏性阻尼,用黏性阻尼系数C表示;另一部分为密封环及运动副导致的舵系统转动过程中由库仑摩擦力产生的阻尼,用Tf表示,θr为舵面转角,Tc为气动控制力对舵轴的力矩,2e为系统的回环间隙,同时为了便于建模,将空气舵角运动等效为线运动的形式进行描述。
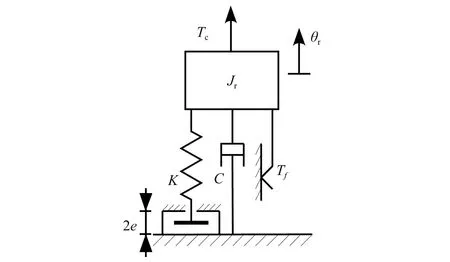
图2 空气舵系统数学模型示意图
舵面的动力学方程为
(1)
(2)
本文分别讨论两种摩擦模型:一种为库仑摩擦模型;一种为Stribeck摩擦模型。
库仑摩擦是非零速下的摩擦,是最早被发现的摩擦现象之一。库仑摩擦力独立于接触面积,与法向载荷成比例,与运动方向相反,而与速度的幅值无关,库仑摩擦模型如图3所示。
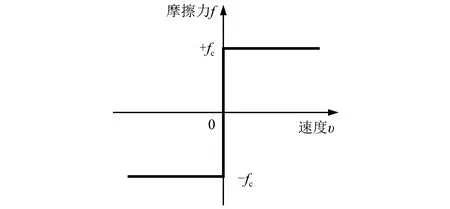
图3 库仑摩擦模型
舵系统库仑摩擦力矩为
(3)
式中,Mf为库仑摩擦力。
Stribeck摩擦模型考虑了Stribeck效应,可以描述低速区的摩擦行为,极大的减少了摩擦的不连续性。Stribeck摩擦随速度的不断增大,摩擦力经历先下降到一个极小值,然后随速度增大而增大的过程,如图4所示[13],共分为三阶段:第一阶段为预滑动(pre-sliding regime)和边界润滑阶段(boundary lubrication),此时的摩擦力来自于固体-固体间的摩擦;第二阶段为部分流体润滑阶段(partial fluid lubrication),此时油膜部分生成,但固体-固体间的摩擦仍大于润滑油的黏性效应;第三阶段为完全润滑阶段(full fluid lubrication),此时固-固摩擦消失,摩擦力来自于润滑油的黏性效应,随速度增加而增大,此阶段也称为流体动力润滑阶段。

图4 Stribeck摩擦模型
舵系统Stribeck摩擦力矩为
(4)
式中:Mf为静摩擦力矩;k1,k3为动摩擦力矩曲线方程系数,具体形式为
(5)
式中:vm为动摩擦力矩最小时的舵面角速度;k0为最小动摩擦力矩与静摩擦力矩Mf之比,当k0=1时,Stribeck摩擦模型退化为库仑摩擦模型。
2 参数识别方法
参数识别的目的是找到一组参数,使模型计算数据与试验数据拟合程度最好。影响参数识别结果的因素有两个:一是机理分析及建模的准确性;二是算法精度。因此,本文选择了两种算法针对两种模型进行参数识别,以达到迭代比较的目的。
2.1 最小二乘非线性拟合法
最小二乘非线性拟合一般包括三个步骤:①获取试验数据;②在结构分析基础上,根据试验数据规律建立含有未知参数的系统动力学特性数学表达式;③利用MATLAB nlinfit函数确定未知参数的数值(参数识别),即得到拟合的规律。
在工程实际中得到系统的频响是非常成熟和方便的,因此已知的观测数据为系统的幅频响应数据。符合幅频响应数据规律的数学表达式为幅频响应函数,但对于不同的摩擦模型,其表达式的形式不同,因此识别结果和拟合效果也不同。基于最小二乘非线性拟合法的参数识别流程,如图5所示。
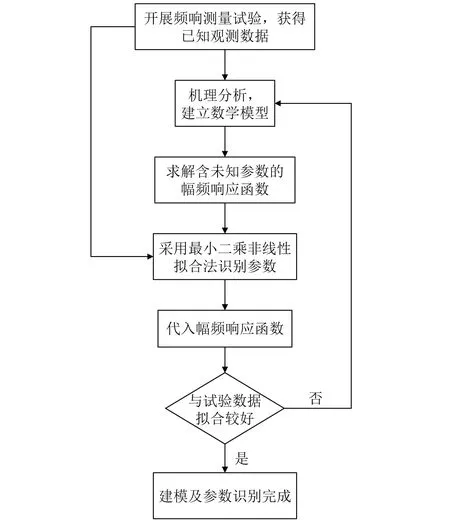
图5 基于最小二乘非线性拟合法的参数识别流程图
幅频响应函数的求解采用谐波平衡法,忽略高次谐波,设在如下正弦激励下
Tc=T0[sin(ωt)cosh-cos(ωt)sinh]
(6)
舵面响应为
θr=θ0sin(ωt)
(7)
式中:T0和θ0为激励力矩和舵面转角的幅值;h为响应与激励的相位差。
将式(6)和式(7),以及库仑摩擦力矩(3)代入式(1)后取出一次谐波项的系数,得到两个谐波平衡方程
4Mf+π[Cθ0ω+T0sinh]=0
(8)
π[T0cosh+Jθ0ω2]+
Kθ0[sin(2φ)-π+2φ]=0
(9)
式中,φ=arcsin(e/θ0)。
通过式(8)和式(9)消去相位差,得到摩擦模型为库仑摩擦模型的舵系统幅频函数方程
(10)
将式(6)和式(7),以及Stribeck摩擦力矩(4)代入式(1)后取出一次谐波项的系数,得到两个谐波平衡方程
(11)
π[T0cosh+Jθ0ω2]+Kθ0[sin(2φ)-π+2φ]=0
(12)
式中,φ=arcsin(e/θ0)。
通过式(11)和式(12)消去相位差,得到摩擦模型为Stribeck摩擦模型的舵系统幅频函数方程
(13)
2.2 遗传算法
遗传算法是一种通过模拟自然进化过程实现最优解搜索的智能优化算法,其优点为适应范围广,鲁棒性强。
遗传算法与最小二乘非线性拟合法的区别在于无需求出函数表达式,但需要设定一个目标函数,优化各参数使目标函数值最小。由于已知的观测数据为系统的幅频响应数据,因此设置的目标函数应能表征模型计算的幅频响应曲线与试验测得的幅频响应曲线的拟合程度,且拟合程度越高,目标函数值越小。基于遗传算法的参数识别流程,如图6所示。
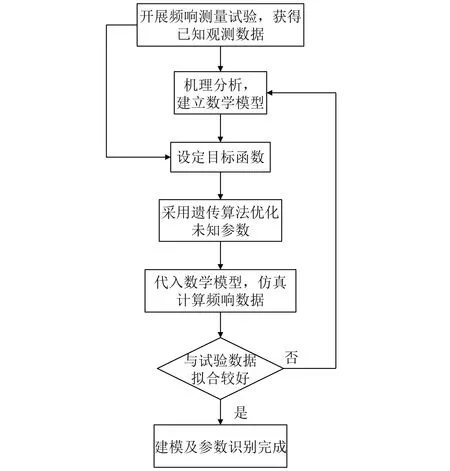
图6 基于遗传算法的参数识别流程图
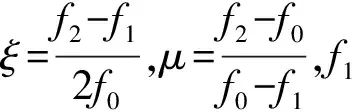
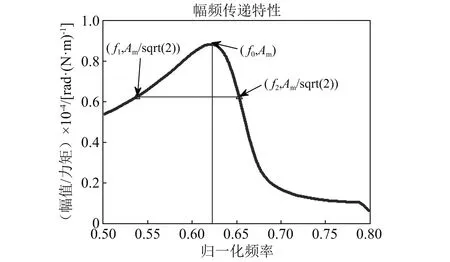
图7 空气舵系统动力学特征参数示意图
目标函数采用统一目标函数法进行优化计算,具有线性加权平方和的形式,具体如式(14)所示
(14)
式中,加权因子wp(p=1,2,…,l)的选取使各分目标函数wpfp(X)成为无量纲的具有等量级数值的函数。各分目标函数为
(15)
式中:H0为试验得到各频率的幅频响应向量;h0为计算得到各频率的幅频响应向量;Y1,Y2,Y3,Y4分别为试验得到的幅频响应曲线的四个非线性动力学特征参数;y1,y2,y3,y4分别为计算得到的幅频响应曲线的四个非线性动力学特征参数。
3 参数识别结果
本文参数识别采用的已知观测数据为试验测得的舵系统的频响数据,各待识别的参数没有确定的理论值,故评价参数识别结果是否有效的标准为将各参数的识别结果代入模型中计算所得的幅频响应曲线与试验测得的幅频响应曲线的吻合程度。
3.1 基于库仑摩擦模型的参数识别结果
将库仑摩擦力矩代入舵系统运动方程中,可以得到摩擦模型为库仑摩擦模型的舵系统非线性动力学模型。该型空气舵的转动惯量为J=0.346 kg·m2,待识别的参数分别为:舵轴的等效扭转刚度K、黏性阻尼系数C、库仑摩擦力Mf、系统间隙e。本节分别采用最小二乘非线性拟合法及遗传算法对所建模型中的未知参数进行识别,识别得到的参数值如表1所示,仿真和试验得到的幅频响应曲线,如图8所示。
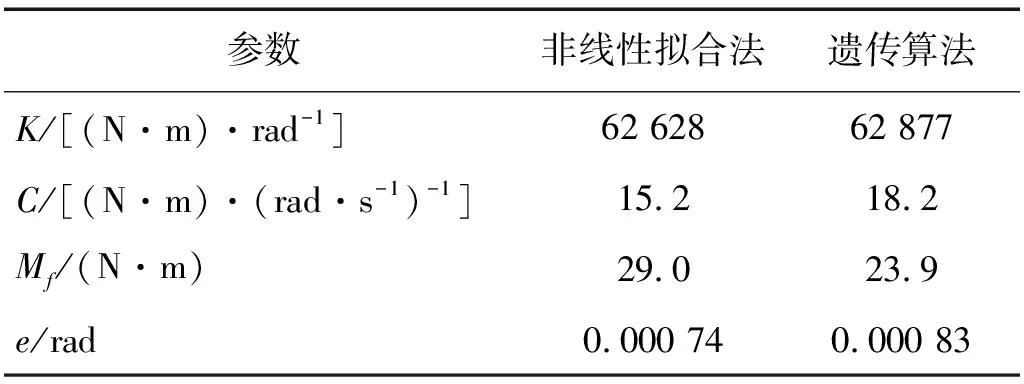
表1 基于库仑摩擦模型的参数识别值

图8 模型计算与试验幅频响应曲线对比图
3.2 基于Stribeck摩擦模型的参数识别结果
将Stribeck摩擦力矩代入舵系统运动方程中,可以得到摩擦模型为Stribeck摩擦模型的舵系统非线性动力学模型。该型空气舵的转动惯量为J=0.346 kg·m2,待识别的参数分别为:舵轴的等效扭转刚度K、黏性阻尼系数C、静摩擦力矩Mf、系统间隙e、最小动摩擦力矩与静摩擦力矩Mf之比k0、动摩擦力矩最小时的舵面角速度vm。本节分别采用最小二乘非线性拟合法及遗传算法对所建模型中的未知参数进行识别,识别得到的参数值如表2所示,仿真和试验得到的幅频响应曲线,如图9所示。
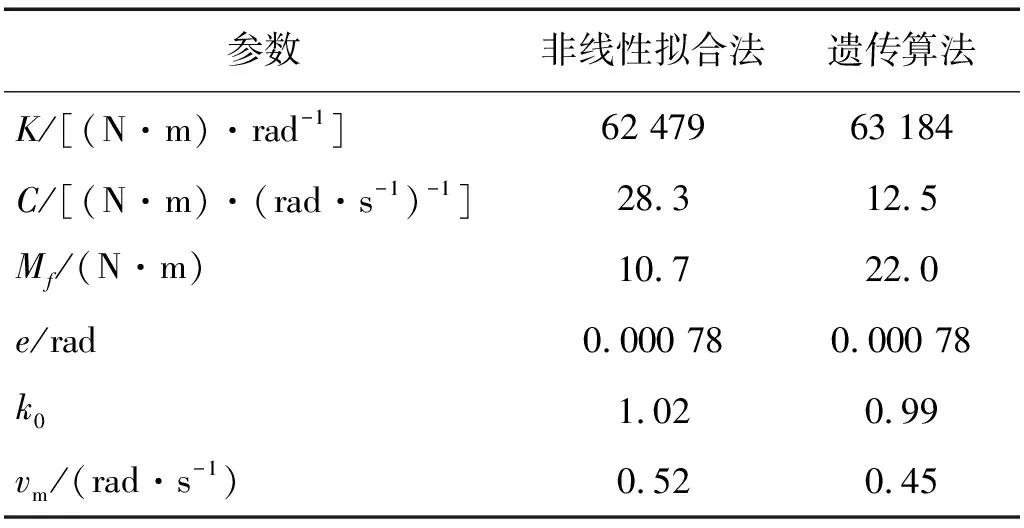
表2 基于Stribeck摩擦模型的参数识别值
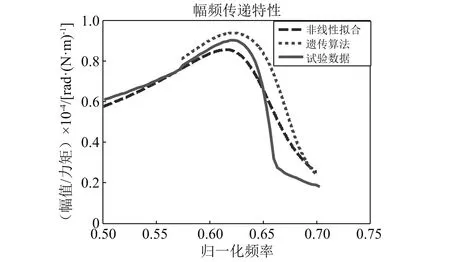
图9 模型计算与试验幅频响应曲线对比图
3.3 结果分析
由识别结果可见:
(1)相较于Stribeck摩擦模型,采用库仑摩擦模型所建立的舵系统非线性动力学模型能较为准确地反映该型空气舵系统实际的动力学行为。基于库仑摩擦模型的参数识别,最小二乘非线性拟合法和遗传算法识别得到的各项参数值差异较小,计算得到的幅频响应曲线与试验测得的幅频响应曲线拟合效果均较好,分析认为参数存在的微小差异的主要原因是不同算法产生的算法误差。
(2)基于Stribeck摩擦模型的参数识别,采用两种参数识别方法得到的最小动摩擦力矩与静摩擦力矩Mf之比k0的值均接近1,当k0=1时,Stribeck摩擦模型退化为库仑摩擦模型,进一步验证了库仑摩擦模型能较为准确地反映该空气舵机械系统的真实摩擦力矩。
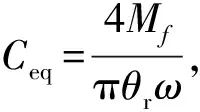
(4)最小二乘非线性拟合法的计算时间短,效率高,但需要求出幅频响应函数的解析解,对于本文研究的单自由度系统较为适用,对于更复杂的无法求出函数表达式的系统并不适用。由于在遗传算法优化的过程中需要仿真计算模型的幅频响应数据,故计算较慢,效率较低,但对于任意系统,都具有可行性。
4 结 论
在飞行器工程研制实践中,由于设计加工制造过程中产生的间隙、摩擦,导致系统的动力学特性存在明显的非线性特征。本文针对典型的战术武器空气舵系统,分别采用库仑摩擦模型和Stribeck摩擦模型建立了空气舵系统非线性动力学模型,并使用试验测得的频响数据识别模型中的未知参数,得到以下结论:
(1)本文通过建模及参数识别,比较了库仑摩擦模型和Stribeck摩擦模型与实际系统的适应程度,结果表明库仑摩擦模型能够较为准确地反映实际系统中的摩擦力矩。
(2)本文比较了最小二乘非线性拟合法和遗传算法参数识别的效果,结果表明这两种算法都能取得较好的参数识别效果,但适用范围及计算效率不同。
后续应在在以下方面开展工作:
(1)采用动态摩擦模型,如Lugre摩擦模型建立舵系统非线性动力学模型,识别模型中的未知参数,并将模型计算结果与试验结果对比判断建模的准确程度。
(2)考虑接触等非线性因素,研究其建模及参数识别方法。
