一种基于高斯近似的极化码打孔算法

李世宝 高 迅 董振威 刘建航 崔学荣

①(中国石油大学(华东)海洋与空间信息学院 青岛 266580)

②(中国石油大学(华东)计算机科学与技术学院 青岛 266580)

1 引言

极化码是目前已知唯一的一种被严格证明达到信道容量的信道编码方法[1]，但是由于极化码编码器是基于克罗内克积生成的[1-3]，极化码的长度总是被限制为 2n，在实际应用中，传输码字的长度不一定都是 2n，经常出现可变码长的实际需求。打孔算法是构造码长可变和码率灵活极化码的重要途径，近年来获得了研究者的广泛关注。

文献[4]首次提出极化码打孔算法，包括随机打孔和停止树打孔两种基本打孔算法，满足了码长可变的要求。文献[5]提出了一种基于删除极化矩阵的打孔算法，通过删除分别对应于打孔位和冻结位的列和行之后分析简化的极化矩阵，相对于随机打孔算法可以获得1.0～5.0 dB的性能增益。文献[6]提出了准均匀打孔方案，通过比特倒置排序使得打孔比特准均匀分布，操作简单且具有较好的译码性能。文献[7]在文献[6]的基础上，提出一种倒置准均匀打孔方案，在高码率下获得更好的性能。文献[8]基于比特倒置策略和前向序列打孔提出一种新的打孔算法，提升了不同码率下的打孔性能。文献[9]提出一种适用于乘积极化码的打孔算法，性能相对于先前打孔的乘积极化码和单极性码更优。文献[10]提出并验证了使用二进制控制可以确定极化码的打孔比特集合。文献[11]结合码字重复技术提出分区打孔的思路，获取了一个更有效的信息比特集合。文献[12]将里德-所罗门(Reed-Solomon, RS)码作为极化码的外码，提出了一种平均分布打孔算法，构造了一种RS-极化码打孔方案，扩展了打孔极化码的应用范围。文献[13]提出了一种在打孔之后使用高斯近似(Gaussian Approximation, GA)对子信道进行重构的打孔算法，进一步提升了打孔算法的性能。上述的打孔算法均需要在打孔之后进行重新构造，但是重构使得算法复杂度增加。针对这一问题，文献[14]提出了一种低复杂度的打孔(Low-Complexity Puncturing, LCP)算法，在极化码构造一次的情况下使用了准均匀的打孔策略进行打孔。文献[15]提出了一种最差质量打孔(Worst-Quality Puncturing, WQP)算法，在固定信息集合下对最差质量信道进行打孔从而获取更好的打孔性能。

现有算法没有考虑信道构造环节对极化码打孔性能的影响，限制了极化码打孔性能的进一步提升。本文从信道构造出发，联合考虑打孔的特点，提出一种基于改进高斯近似的极化码打孔(Puncturing Polar Code based on Gaussian Approximation, GAPPC)算法。

2 极化码

高斯近似函数的近似推导和提出第1次出现在文献[18]，然后该函数被应用于极化码的高斯近似构造中。现在基于高斯近似构造的极化码算法都基本上沿用了该公式，该高斯近似函数如式(4)所示

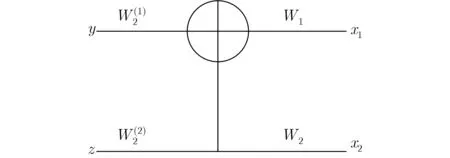
图1 基础的蝶形计算结构

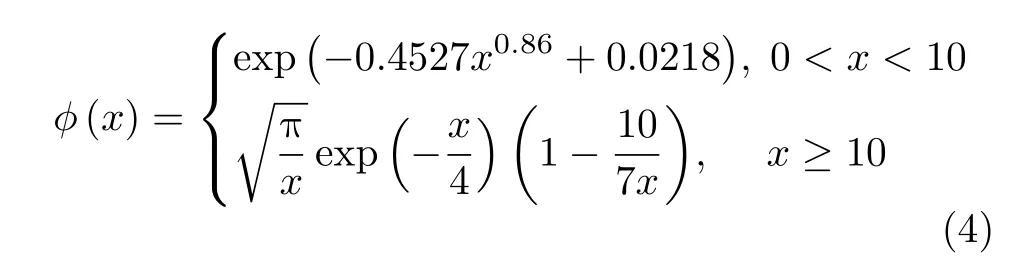
3 基于改进高斯近似的极化码打孔算法

GAPPC算法主要思想是通过改进信道构造环节，提升打孔算法性能。首先引入高斯修正因子，改进高斯近似函数，得到子信道的可靠性排序集合。其次依据信道容量关系推导出改进的信道映射规则，对选出的无能力比特集合进行映射得到打孔比特集合，并结合可靠性排序集合完成打孔极化码构造，最后给出GAPPC具体算法流程。

3.1 改进高斯近似函数

另外，式(6)中的λ0,λ1对α的求导结果为

3.2 信道映射

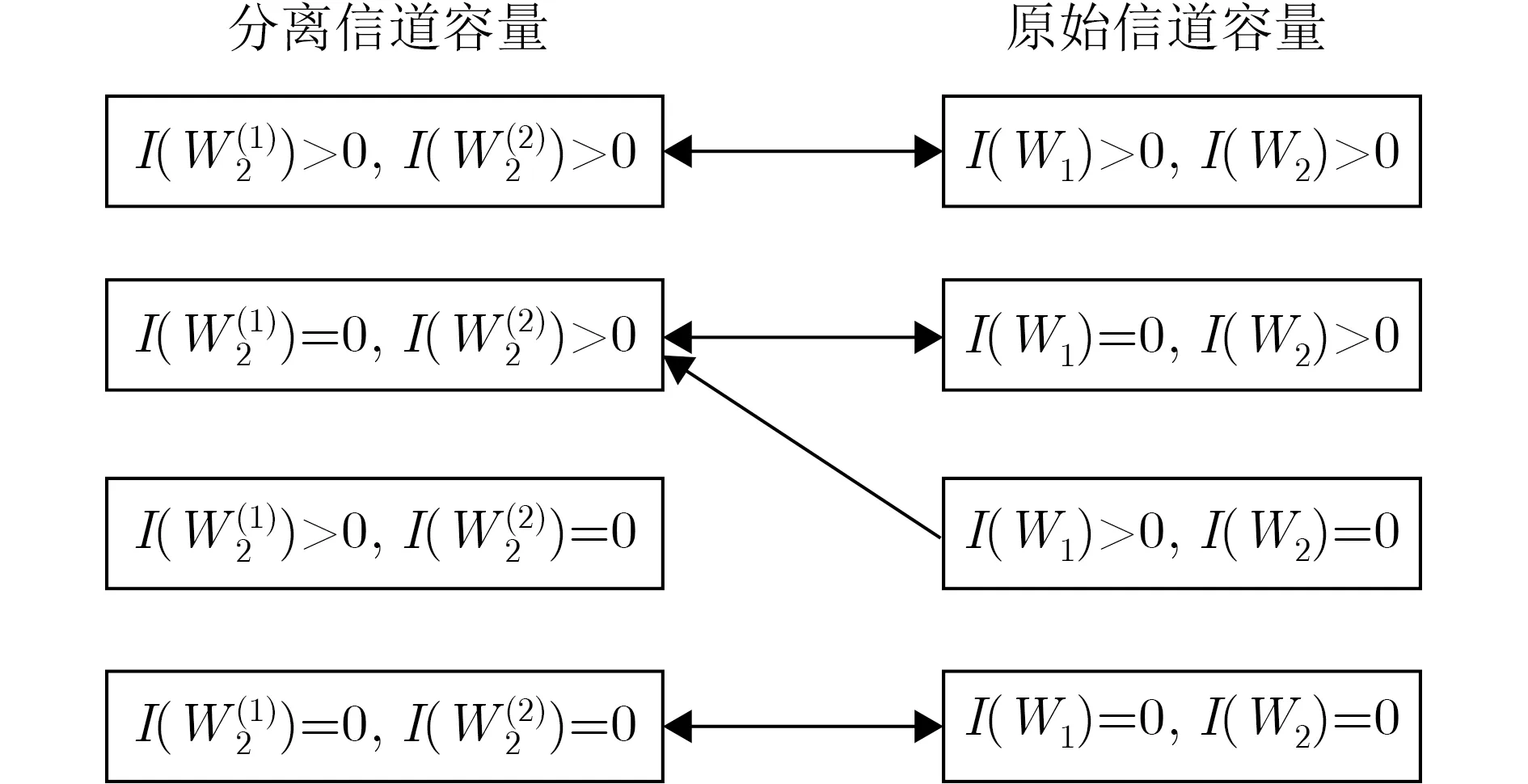
图2 蝶形计算中信道容量关系

3.3 算法流程

将MGA引入构造，得到MGA构造，将MGA构造出的子信道按照升序排序得到的序列集合设为RMGA。结合MGA构造和推导出的映射规则，提出GAPPC算法，算法具体如表1所示。

表1 GAPPC算法

在GAPPC算法中，首先对N长的极化码进行MGA构造，按照LLR值升序得出子信道的可靠性序列RMGA。 选出无能力打孔位置集合Q={1,2,...,P}，即uN1的前P比特作为无能力比特，P=N −M，应用Q和改进的映射规则在极化码编码结构中迭代，找出打孔比特集合P。根据RMGA和Q，获取无能力比特之外的最不可靠的M−K比特，作为剩余冻结集合QC。根据QC和Q可 以得到冻结比特集合AC和信息比特集合A，完成对打孔极化码的构造。

在完成极化码构造之后，对N长码字uN1进行编码得到xN1，并运用打孔比特集合P对编码后码字进行打孔得到M长传输码字y1M，得到(N,M,K)打孔极化码，码率为K/M。在传输过程中打孔比特不会被发送，在接收端，译码器会将打孔比特的LLR值设置为0并完成最终译码。

4 实验与结果分析

实验采用二进制相移键控调制信号源信号，传输信道采用AWGN信道，极化码译码采用串行抵消译码算法。实验中对比了LCP算法、WQP算法、文献[10]的打孔算法(BD算法)以及所提GAPPC算法之间的误码率(Bit Error Rate, BER)和误帧率(Frame Error Rate, FER)性能。实验中使用的极化码码长为512和256，使用的码率为2/3,1/2和1/4。另外，每次实验的最大模拟帧数为 107，如果有1000个错误帧或共传输了 107帧，实验将会停止。

图3展示了码率为1/2，码长分别为512和256下，4种极化码打孔算法的FER和BER性能对比。图3(a)显示了极化码码长为512，打孔后码长为372，码率为1/2时，GAPPC算法与LCP算法、WQP算法和BD算法的性能对比。相对于WQP算法、LCP算法和BD算法，GAPPC算法的BER性能在SNR为1～4 dB时均有一定的提升，且BER在10−3可以获得至少0.3 dB的性能增益。而GAPPC算法的FER性能明显优于其他3种打孔算法，FER在1 0−2至少获得0.75 dB的性能增益。图3(b)显示了在极化码码长为256，打孔后码长为186，码率同样为1/2时，GAPPC算法的FER和BER性能均明显优于其他3种算法，BER在10−2至少可以获0.25dB的性能增益，FER在1 0−2至少可以获得0.5 dB的性能增益。GAPPC算法在选择信息集合和冻结集合时使用的是基于MGA构造的子信道，依据子信道的LLR值获得可靠性排序集合，选择可靠性高的信道传输信息比特。这样构造出来的极化码能降低打孔带来的信道降级影响，从而可以获得更好的性能。由以上分析可知，在不同码长相同码率下GAPPC算法具有显著的性能提升，且极化码码长越大，算法性能提升越多。

图4展示在码长为512，码率分别为2/3和1/4时，4种算法之间的FER和BER性能对比。图4(a)显示了在极化码码长为512，打孔后码长为360，码率为2/3时，GAPPC算法与LCP算法、WQP算法和BD算法的性能对比。在SNR为1～3 dB时，GAPPC算法与WQP算法的BER相近，明显优于LCP算法和BD算法；而在SNR为4 dB时，GAPPC算法的BER性能优于另外3种算法。而对于FER性能，GAPPC算法在SNR为1～4 dB时均具有显著的性能优势。图4(b)显示了在极化码码长为512，打孔后码长为400，码率为1/4时，GAPPC算法的BER与FER性能具有显著的提升。在SNR为4dB时，GAPPC算法的FER可以达到 5×10−5，BER达到6×10−6，相对于LCP算法、WQP算法和BD算法，GAPPC算法性能提升10倍以上。再结合图3(a)的实验结果可知，在相同码长不同码率下，GAPPC算法均可以获得显著性能增益，且码率越小，性能增益越大。

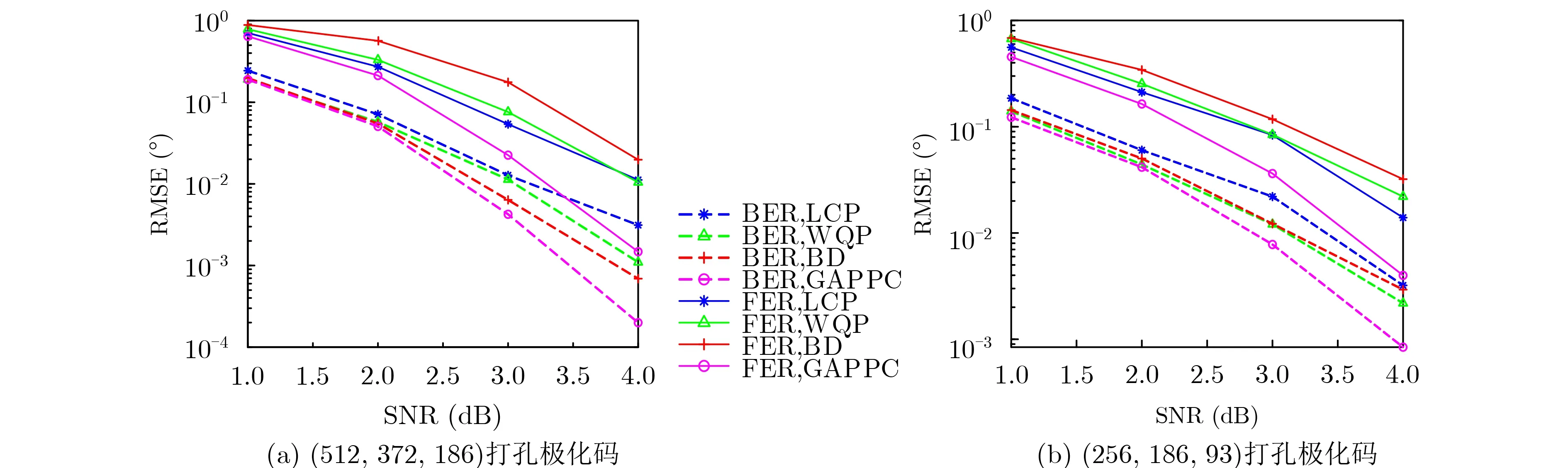
图3 不同码长相同码率下的4种极化码打孔算法性能对比

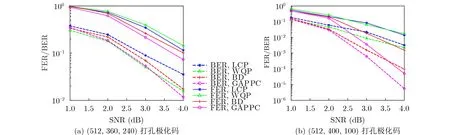
图4 相同码长不同码率下的4种极化码打孔算法性能对比

表2显示了不同打孔情况下，WQP算法的复杂度略高于LCP算法的复杂度，BD算法与LCP算法复杂度一致，而GAPPC算法的复杂度在4种算法中最高，其中LCP算法、WQP算法和BD算法都需要GA构造和比特倒置排序。由文献[16]可知，GA构造的复杂度为O(NlgN)。LCP算法中，通过比特倒置排序得到的打孔比特集合会被预先设定，LCP算法只需要进行选择即可获得打孔比特集合，因此算法复杂度为O(NlgN)+O(1)。而WQP算法选取S位无能力比特后进行比特倒置操作，因此算法复杂度为O(NlgN)+O(S),S=N −M。BD算法与LCP算法相似，同样只需对预设集合进行选择即可获取打孔比特集合，因此BD算法的复杂度与LCP算法一致。二者的区别在于BD算法的预设集合是利用二进制控制特性[10]排序后经过比特倒置操作获得的，而LCP算法的预设集合则是利用自然序与比特倒置操作获取的。预设集合在算法进行前完成设定，因此不计入算法复杂度。GAPPC算法的复杂度主要来自MGA构造以及信道映射，MGA构造的复杂度与GA构造的复杂度相同，都是O(NlgN)，而信道映射的复杂度为O(SlgN)，因此算法的复杂度为O(NlgN)+O(SlgN)。根据上述分析可知，相比于其他3种算法，GAPPC算法由于信道映射而具有更高的复杂性。

表2 4种算法的计算复杂度对比

5 结束语

为了进一步提升极化码打孔算法的性能，在极化码打孔算法中联合考虑打孔和构造，提出高斯修正因子，并推导出最优的高斯修正因子和相应的MGA，依据信道容量的关系推导出改进的信道映射规则，找到打孔比特集合。基于MGA构造和改进的信道映射规则，设计了GAPPC算法并进行相关的实验验证。实验结果显示，在不同的码长和码率下，与LCP算法、WQP算法和BD算法相比，本文所提GAPPC算法的FER和BER性能均有显著提升，且码率越低码长越大获得的性能增益越多，但算法的复杂度会略有增加。