波浪驱动推进机构的最优水翼倾角的确定*
2021-12-02常宗瑜于振江郑中强冯展霞张嘉坤孙秀军王攀峰
常宗瑜, 于振江, 郑中强, 冯展霞, 张嘉坤, 孙秀军, 王攀峰
(1.中国海洋大学工程学院, 山东 青岛 266100; 2.机构理论与装备设计教育部重点实验室, 天津 300072;3.中国海洋大学 山东省海洋重点实验室, 山东 青岛 266100)
随着全球矿物燃料资源的日益枯竭和环境污染的日趋加剧,对清洁的、可再生的海洋能源的有效利用已成为当前世界上主要沿海国家的战略性选择。波浪能具有蕴藏丰富、分布面广、可以就地采能等特点,若转化为船只的推进动力,则其可获得近乎无限的续航能力。将波浪能作为驱动船只的能量来源作为优先主题被提出[1]。早在1895年就出现了波浪能驱动船的专利,在此之后,研究人员设计并制造了一系列的波浪船的实验模型[1]。日本在1980年提出了波浪能驱动装置Wave Devouring Propulsion System (WDPS)的概念[2-3],并制作了模型船并进行了海上试验研究。后续Terao等[4]继续对WDPS系统进行了研究,在2000年[5]提出了一个新型的双体船结构的WDPS系统,采用了两个可以独自运行的双翼片驱动结构。在大量实验的基础上‘Mermaid II’制造成功并在2008年进行了跨太平洋航行,完全基于波浪能驱动从夏威夷岛到达日本[6],航程累计达7 800 km。Bøc kmann[7]提出可以通过对推进翼片的恢复弹簧刚度设计和翼片运动控制,实现对波能船运动性能的优化。2015年Terao[8]对波能船进行了数值分析,在此基础上设计制作了原始模型船,在实验水槽及近海进行了实验。实验证明了波浪能吸收船可以成为海洋监测的有力工具。
与此同时,众多学者对波能船的水动力学进行了研究。Politis等[9]通过对翼片的主动控制可以有效利用波浪能推进,并对水翼后部形成的尾迹进行了研究。De等[10]对推进翼片在自由表面波浪激励下的水动力学进行了研究。Bowker等[11-12]提出了一种利用翼片摆动的能量回收装置,以便高效利用波浪能驱动。杨富茗等[13]采用多软件交互的方式实现了波浪滑翔机水下推进机构的流固耦合动力学分析。郑炳欢等[14]给出了波浪滑翔机的推进机构翼片的优化角度,分析了翼片角度与推进速度之间相互关系
为了对波能船的性能进行研究,众多学者[15-18]建立了波能船的多体动力学方程对波能船的动力学响应进行了分析。但推进性能同环境参数、推进装置运动参数的关系仍需进一步研究。
本文建立了波能船的多体动力学模型。采用凯恩方法得到了系统的耦合运动方程。通过对系统的运动方程的内在关系进行分析,探讨了波能船运行速度同翼片偏转角度及波浪参数的关系。基于最大的推进力,得到了翼片最佳的偏转角度的经验公式。该研究对于波能船的设计具有指导意义。
1 动力学模型建立
1.1 模型简化
波能船的简化模型如图1所示,首先建立坐标系。坐标系共有两个,一个是O-XY与大地相连的绝对坐标系,另一个是与翼片相连的相对坐标系o-xy(见图1)。其中,翼片的偏转角度为θ1,翼片的重心坐标为(x2,y2),并且x轴与X轴平行。

((a)浮体向下运动 Floating body downward;(b)浮体向上运动Floating body upward.)
当浮体向上运动时,翼片向下偏转(见图1(a))产生推进波能船前进的动力,当浮体向下运动时,翼片向上偏转(见图1(b))同样可以产生推动波能船前进的动力。因此不论浮体向上运动还是向下运动都可以产生推动波能船前进的动力。
为模型的建立,作了如下假设:
(1) 在波浪的激励下,水面浮体只会随之产生垂荡和前进方向上的运动。而其它运动,如俯仰和横滚等运动将会被忽略不计;
(2) 水的流动和流动速度等忽略不计,假设波能船是在静止的水中前进的;
(3) 中间缆绳一直保持张紧状态,且水面浮体的重心与缆绳吊点的位置重合;
(4) 翼片上的水动力是来自于水在翼片表面产生的压力分布,因翼片转动而产生的涡流和尾流忽略不计,将翼片表面受到的力简化看成是翼片重心点上受到的力。采用弗劳德-克雷洛夫力来计算水流力,并对弹性阻尼进行了线性化处理。

1.2 偏速度


表1 偏速度表达式Table 1 Velocity formula
(1)
(2)
(3)
1.2 广义主动力
翼片上面受到的水动力对整个波能船系统的前进具有重要的作用。一般来说,将其分为切线方向上的力和法线方向上的力,且往往切线分量要比法线分量小许多。因此,水动力可以近似的通过下面方程来计算:
(4)
式(4)中所示,U是翼片的相对速度;ρ是海水的密度;S是翼片受力的投影面积;Cd是水阻力系数。本节中水动力问题可简化为:
(5)

图2 翼片受到的水的作用力与速度的关系Fig. 2 The relative velocity of fluid on fin and the hydrodynamic force on fin
为了得到翼片上的力,而计算切线和法线方向上的速度:

(6)
根据Froude-Krylov公式,翼片上面所受到的力的方向应该与翼片的速度方向相反,因此水的作用力表示为:

(7)
此力在坐标系中可表示为:
(8)
从翼片的扭转弹簧参数可以得到广义矩阵:
(9)
波能船的主动力包括前进方向上的力Fcx2和垂直方向上的力Fcy2:
(10)
水面浮体的浮力和重力为上下振荡运动提供了恢复力:
(11)
上面公式中,m2是水面浮体的质量;g是重力加速度,A是横截面面积;y20是静力平衡条件下的吃水深度;y2是平衡位置上的吃水深度的位移变量。
(12)


(13)
1.3 广义惯性力
依据表1中的各速度的表达式,来求解相应的惯性力:

(14)

(15)

(16)
(17)
(18)
(19)
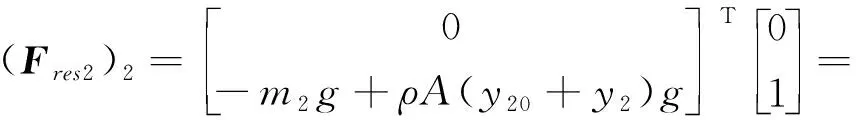
(20)
(21)
(22)
(23)
1.4 动力学方程
通过以上推导过程,波能船的积分方程如式(24~26)所示:
(24)
(25)
(26)

表2 波浪能吸收装置参数Table 2 Parameters of wave powered boat
2 结果和分析
如图3中所示,(a)图中表示的是波能船在X方向上的位移,在600 s的时间内行走约87 m的距离;(b)图中表示的是波能船在X方向上的速度曲线,选取速度达到稳定后的一段进行分析,平均速度约为0.153 m/s;(c)图中表示的是翼片转角的角位移与角速度随时间的变化曲线,图中虚线所示为角度曲线,实线表示角速度且最大约为0.2 rad/s。(d)图中波能船表示的是Y方向上是位移与速度曲线,图中实线所代表的其实就是初始条件中设置的幅值0.5 m、周期2.923 s的正弦函数曲线,图中虚线表示的是Y方向随时间而变化的速度;
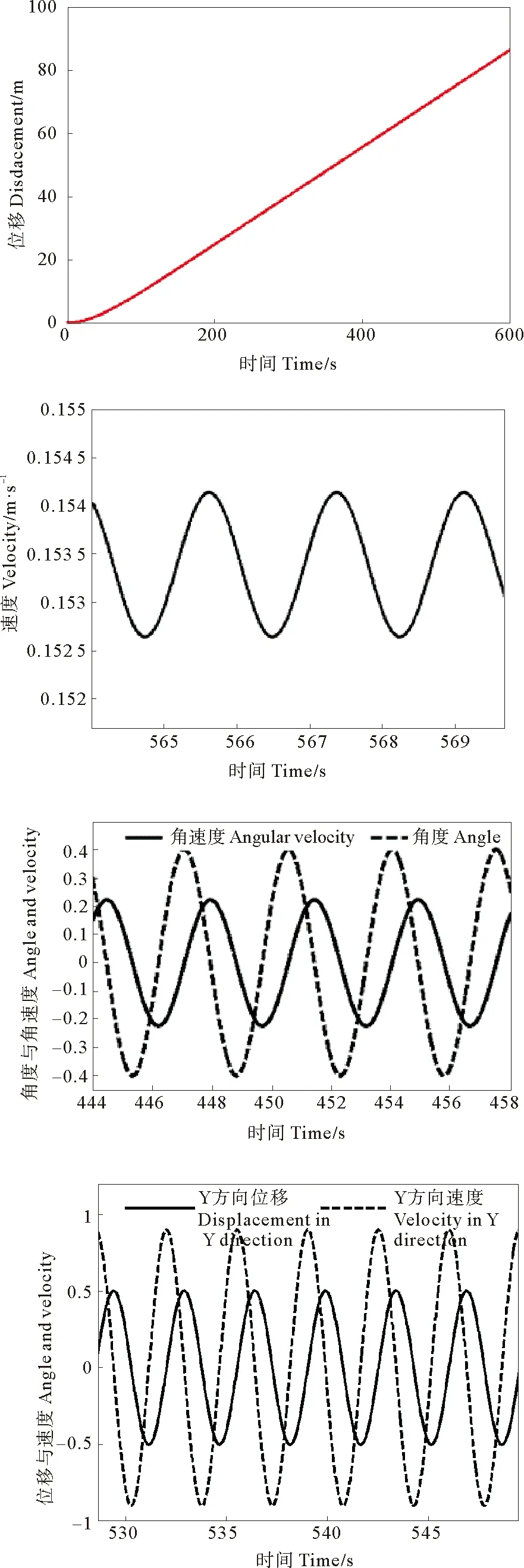
(a. X方向位移曲线 Displacement in X direction;b. X方向速度曲线 Velocity in X direction;c. 角度与角速度 Angle and angular velocity;d. Y方向位移与速度曲线 Displacement and velocity in Y direction.)
通过以上公式的求解,可发现系统的推进力来源于水动力。由公式继续推导,可以得到X方向、Y方向以及翼片转角三部分所产生的水动力,公式如下所示:
(28)
(29)
(30)
为了研究这三部分力分别对波能船的推进具有多大的贡献,通过数值求解的办法来求解这三个值的大小,并求三个力的合力,所得结果如图4所示。点画线代表X方向上产生的推进力,全部为负值,也就是说X方向上产生的力是水阻力;点线代表的是翼片转角所产生的推进力,其大小在0值上下浮动,也就是大致在前进力与阻力之间相平衡;虚线代表的是Y方向上产生的推进力,很明显这是构成整个系统前进推进力的重要来源。综上所述,可以得出波能船推进系统主要力的来源是垂荡运动所产生的力,这与波能船的推进原理相吻合。

图4 推力随时间的变化Fig. 4 Changes of thrust with time
翼片转动产生的推进力在0上下波动,因此忽略,波能船的推进力主要由两部分构成,X方向所产生的水阻力及Y方向的垂荡产生的推进力:
Fp12=Fp1+Fp2。
(31)
(32)
通过对此方程的分析求导,基于费马定理求解临界点,可以分析推进力与翼片偏转角度的关系。

(33)
得到翼片最佳偏转角度的公式:
(34)
当波能船的处于启动阶段时,式(34)可以简化为:

(35)
得到:
(36)
当波能船没有前进速度,处于启动阶段时,只有垂荡运动时采用45°角度可以获得最大的推进力。
3 结语
本文基于凯恩方法建立了波能船的多体动力学模型。推导出了考虑波浪激励力、水的作用力及恢复弹簧力在内的运动方程。通过对运动方程的求解,得到了系统在时域下的响应。基于对方程组成部分的分析,对提供波能船运动的力的贡献大小及组成进行了研究。波能船前进的动力主要来源于浮体的垂荡运动。浮体在x方向的运动起阻碍作用。翼片的摆动所产生的推进力呈现周期性变化,在整个周期中推进力及阻力相互抵消,不考虑所形成的涡流的情况下,对推进力的贡献可以忽略不计。