几种粗糙散射理论对海面中频后向声散射的有效性研究*

戚乐华， 刘保华， 阚光明,3

(1.中国海洋大学海洋地球科学学院，山东 青岛 266100； 2.青岛海洋科学与技术试点国家实验室，山东 青岛 266237；3.自然资源部第一海洋研究所海洋沉积与环境地质重点实验室，山东 青岛 266061)

海面声散射是水下目标探测和识别时混响背景的主要来源，是限制水下声呐和通讯系统表现的重要因素之一[1-2]。尽管对于海面声散射的散射机制和特性还没有完全弄清楚，但是经过七十多年的研究，已经发展形成了多种声散射模型、理论及计算方法，并达成许多重要的共识。一般来说，海面声散射可分为粗糙散射和气泡散射两部分，其中气泡散射主要在小掠射角和大风速条件下产生重要影响，由海面上下起伏引起的粗糙散射在中高掠射角占主导[3-4]。

目前，对于粗糙散射的研究已经形成多种成熟的理论和近似计算方法，其中许多方法同时应用于声散射和电磁散射领域[5]，如Kirchhoff近似、小粗糙微扰近似、小斜率近似、复合粗糙理论等。上述这些方法均采用了相应的近似模型，是特定条件下的近似结果，因此只有在特定条件下才具有较好的预测精度。而积分方程法[6]在物理上没有做任何的近似，同时还考虑了界面的多重散射现象和影区作用，在物理上是严格精确的，因此该方法常作为衡量其他粗糙散射近似方法有效性和准确性的标准。其它粗糙散射近似计算方法还有全波法、相位微扰法、算子展开法、统一微扰法等，但是这些方法存在适用范围太窄、计算比较困难等缺点，在实际应用中没有得到推广[7]。

一般来说，Kirchhoff近似在双基地前向散射方向，特别是镜面反射方向准确度较好，而微扰理论在远离镜面反射方向的预测精度较高[8-10]。Thorsos和Jackson等[8]对微扰近似在高斯粗糙谱下有效性进行了研究，在kh<0.6,kL<2条件下最低阶微扰理论就具有较高的预测精度。当计算至更高阶微扰理论时，具有相同精度的相关长度范围进一步扩大。Thorsos还研究了高斯粗糙谱下Kirchhoff近似的有效范围，认为表面相关长度是影响其准确性的最重要参数[11]，当kL>6时Kirchhoff近似精度优于1 dB。结合上述两种方法的特点，形成了复合粗糙理论[12]将粗糙面人为的划分成大尺度和小尺度两个部分。海面散射主要由小尺度粗糙引起，大尺度粗糙则改变散射掠射角。该方法非常依赖区分大小尺度的截止波数的选择，如果截止波数选择的不合理，会导致理论预测与真实值出现较大偏差。而且复合粗糙理论的初衷之一是为了提高计算效率，目前计算机的计算能力已经能够满足高精度的小斜率近似等的计算需求[10]，因此本文未对该方法开展有效性研究。Broschat和Thorsos研究了小斜率近似，发现其在特定条件下可以分别简化为Kirchhoff近似和微扰近似，因而具有上述两种方法共同的优点[7,13]。此外，上述研究结果大多都是基于高斯粗糙谱获得的，实际海面粗糙起伏并不是高斯分布的，常用实际海面粗糙谱多采用“Pierson-Moskowitz”(PM)海浪谱。而且其研究频率主要集中在几百赫兹的低频段，没有考虑1 kHz以上的中高频段。

本文回顾了几种经典粗糙散射理论，利用积分方程法研究了在中频PM海浪谱压力释放边界条件下单基地后向散射的准确性，比较这些方法的有效范围和差异，并利用实测结果验证上述粗糙散射理论在中频频段(1～20 kHz)的有效性和可行性。

1 海面粗糙谱和粗糙面的模拟

1.1 PM海浪谱

海面粗糙散射的计算有赖于海面粗糙起伏特征的准确描述，粗糙度谱W(K)是绝大多数声散射模型和方法的重要输入参数，它与粗糙面相关函数互为傅里叶变换对，利用其可以计算得到海面的均方高度、均方斜率等。

(1)

(2)

式中：h2为均方高度；δ2s为均方斜率；K为空间波数。根据Bragg散射理论，只有与入射声波波长相当的粗糙度特征才是引起声散射的主要原因，较大尺度的起伏则会引起掠射角的改变。

一些研究中采用了高斯谱研究了粗糙散射理论的有效性[8,11]，但是其并不符合实际海面的粗糙起伏特征。目前海洋学家已经对海面粗糙起伏进行了深入的研究，并形成了多种海浪谱模型，如PM海浪谱、Fung海浪谱、JONSWAP海浪谱等。其中PM海浪谱是一种稳态海浪谱，具有形式简单、输入参数较少、应用广泛等特点。PM海浪谱描述的是风持续足够长时间，海浪已经完全成长的情况。此时海浪谱只与风速有关。PM海浪谱的空间域形式为：

(3)

式中：参数α=8.1×10-3；β=0.74，K是空间波数；g为重力加速度，一般取g=9.81 m/s2；U19.5为距海面19.5 m高度处的风速，单位m/s。

根据式(1)可以计算得到海面起伏的均方波高：

(4)

谱峰值对应的波数为：

(5)

可见海面均方根高度与风速的二次方成正比，随着风速的增加海面的均方根高度越大，同时谱峰值对应的波数减小。本文海面散射的研究均是在PM海浪谱条件下进行的。

1.2 线性滤波法模拟粗糙面

一些粗糙散射理论需要根据实际的粗糙面进行计算。如积分方程法、蒙特卡洛Kirchhoff近似、蒙特卡洛小粗糙微扰近似等[8-9,11]。模拟粗糙面的方法称为蒙特卡洛法，有时又被称为线性滤波法。它的基本思想是将随机粗糙面看作是一系列频率谐波叠加的形式，而每个谐波的振幅都是独立的高斯随机变量，其方差正比于对应波数的功率谱。模拟一维粗糙面的公式为：

。(6)

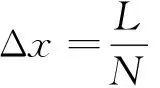
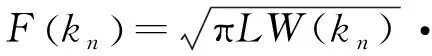
(7)

式中N(0,1)表示均值为0，方差为1的正态分布的随机数。

图1所示为模拟不同风速下的PM海浪谱海面，可以看到风速越大，海面的起伏越大，对应的波长也越长，这与实际的海面情况是相符合的。

图1 模拟不同风速PM海浪谱海面Fig. 1 Surface realization with PM spectrum of different wind speeds

2 粗糙散射理论

2.1 小粗糙微扰理论

小粗糙微扰理论最早基于Rayleigh假设，后来又发展了基于消光定理的小粗糙微扰方法。但是Jackson等[14]研究发现，上述两种微扰方法至少对于前五阶kh是相等的。需要注意的是基于Rayleigh假设的微扰理论的一阶散射截面并不包含多重散射效应。小粗糙微扰理论适用于粗糙面均方根高度远小于声波波长时的情况。一般来说其需要满足kh≪1，其中k是声波波数，h是粗糙面均方根高度。鉴于实际海浪的高度和频率与声波波长的关系，该方法多用于低频的声散射研究。Thorsos研究了小粗糙微扰近似在高斯粗糙谱和PM海浪谱低频双基地情况下的有效性，发现在高斯谱下的误差小于1 dB的条件是kh<0.6，在PM海浪谱下相应的kh可增大至1.79[8-9]。

小粗糙微扰近似的基本思想是利用入射平面波和传输T矩阵来表示散射声场，对于海气界面总声场满足压力释放边界条件。将T矩阵和垂直方向的指数项分别在kh处展开为幂级数形式，然后对每一阶kh的表达式分别应用压力释放边界条件，从而可以获得不同阶的传输矩阵，并进一步求解不同kh阶数的散射截面，其中kh的奇数阶项为零。详细理论介绍可参见Thorsos等[8]的研究。对应(kh)2的散射截面：

(8)

对应(kh)4的散射截面有两项分别是：

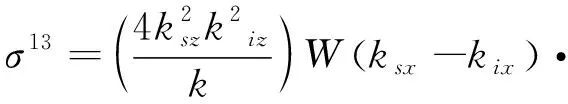
(9)

(10)

其中

(11)

式中：k是声波波数；下标i和s分别代表入射和散射方向，其不同方向的分量分别用下标x和z来表示；h是粗糙面均方根高度；σ(2)=σ11称为二阶散射截面，四阶散射截面σ(4)为：

σ(4)=σ11+σ22+σ13。

(12)

散射截面与散射强度S的关系为S=10log10σ。

2.2 Kirchhoff近似

Kirchhoff近似认为声波在海面上处处发生镜面反射，因此又被称为切平面近似。适用于表面曲率半径远大于入射波长的情况，一般在高频和大粗糙起伏时才符合这种假设。该方法没有考虑影区遮蔽的影响，中小掠射角精度较差，在镜面反射方向附近则具有较好的准确性。根据Thorsos等[9，11,15]的总结，有Kirchhoff近似的海面非相干散射截面如下：

(13)

其中

(14)

C(x)是表面相关函数，

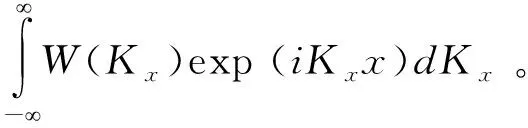
(15)

式中：v=ki-ks是入射波矢量和散射波矢量的差；vx和vz分别是对应方向的波数分量。

2.3 小斜率近似

小斜率近似最早于1985年由Voronovich提出，该理论利用广义表面斜率系统的阐述了界面散射机制和方法。传输矩阵T在小粗糙表面情况下可以简化为小粗糙微扰理论的标准形式，在镜面反射方向小斜率近似又会趋近于Kirchhoff近似。与小粗糙微扰近似相类似，通过将小斜率方法展开到更高的阶次，可以获得更高精度的计算结果。一般情况下，仅使用最低阶小斜率近似就能够获得比传统粗糙散射理论更好的效果，因为它仅使用一个近似就可以完全涵盖所有的入射和散射角度，而且几乎没有精度上的损失[10]。Thorsos和Broschat从理论和数值模拟方法上研究了小斜率近似方法的准确性，发现小斜率近似方法的准确性主要与粗糙面均方根斜率角、表面相关长度和入射掠射角有关[13]。根据Broschat、Thorsos等[5,7,13]的研究，二阶小斜率近似散射截面表达式：

(16)

式中J和v的定义与Kirchhoff近似方法中的定义相同。此外，可以发现二阶小斜率近似与Kirchhoff近似有如下关系：

(17)

其中

(18)

特殊的在镜面反射方向上μ2=1，此时二阶小斜率近似与Kirchhoff近似完全相等。

2.4 积分方程法

积分方程法基于亥姆霍兹积分方程，其在物理上没有做任何的近似，包括了界面的影区遮蔽、多重散射和衍射散射作用，因此常作为其它近似方法的检验标准。积分方程有两种形式，利用海气界面边界条件可以得到一类线性积分方程为：

(19)

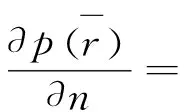
(20)

两种积分方程的计算方法和结果基本相同。下面以一类线性积分方程为例，简要介绍其计算方法。首先将积分方程在海面处离散化：

(21)

上式可化为矩阵方程的形式。

(22)

其中

(23)

(24)

为了避免有限表面长度导致的边缘效应，入射声场可采用锥形平面波形式:

(25)

式中ρ是锥形化参数，一般取ρ=L/4。通过矩阵运算可以计算得到未知的声压法向导数。将声压法向导数带入到(19)式可以计算散射声场和散射强度。积分方程还可以通过粗糙面的周期延拓来计算[16-17]，但是有学者研究发现在较大表面斜率情况下，部分拓展方法是病态的[18]。由于积分方程法需要利用实际的粗糙面计算，而模拟粗糙面的长度和数量有限，导致最终计算结果会出现一定波动，通过增加粗糙面的次数和长度可以减小计算结果的起伏，但相应的计算量也会大幅增加。

3 中频后向散射仿真比较

本文基于PM海浪谱海面，通过积分方程法来检验其在中频后向散射的有效性，其中积分方程法是通过50次模拟海面计算得到。根据积分方程法计算近海面声场如图 2所示，粗糙面利用5 m/s风速PM海浪谱模拟得到，此时海面均方根高度h为0.133 m。图2(a)频率为400 Hz，对应声波波长约3.75 m，图2(b)频率为10 kHz，对应声波波长约0.15 m。可以看到，400 Hz的声波波长远大于海面的粗糙起伏，散射声能量主要集中在镜面反射方向。而10 kHz的声波波长与海面粗糙起伏相当，声能量被散射到非常宽的角度范围。同时需要注意的是近海面声场存在较强的干涉效应，此处的声场不稳定，因此在实际海面散射强度测量时，需要满足远场条件。

(风速为5 m/s，入射掠射角30°。Wind speed is 5 m/s and incident grazing angle is 30°.)

图3所示为利用积分方程法计算海面双基地散射强度，可以看到在中频条件下，绝大部分掠射角范围，总散射强度与非相干散射几乎完全相等(图中两条曲线几乎完全重合)。相干散射强度远小于非相干散射强度，非相干散射平均强约20 dB。只在小风速(3 m/s)的镜面反射方向(150°)相干散射才会占主导。总体来看，在镜面散射方向附近散射强度最强，而后向散射方向散射强度较小。

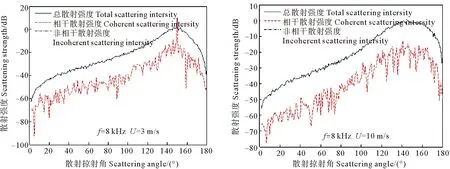
(频率8 kHz，入射掠射角30°。Frequency is 8 kHz, Grazing angle is 30°. )

图 4为不同风速下二阶和四阶粗糙微扰单基地后向散射截面与积分方程法比较的结果。其中σ11代表二阶粗糙微扰近似散射强度，σ11+σ22+σ13代表四阶粗糙微扰近似结果。计算声频率为8 kHz，对应声波波长约0.188 m。3 m/s时海面均方根高度为0.048 m，此时kh=1.61，在小粗糙情况下二阶散射截面就具有相对较高的预测准确性。随着风速的增加海面的粗糙起伏越来越大，二阶散射截面的准确性逐渐降低，而四阶散射截面则仍然具有较好的预测精度，总体来看小粗糙微扰近似在中小掠射角范围的准确性最好。在近垂直入射(掠射角大于80°)时，后向散射方向接近镜面反射方向，此时小粗糙微扰近似的结果明显偏高。此外，在大粗糙(10 m/s)掠射角小于10°的极小掠射角范围，小粗糙微扰近似的准确性也偏低。

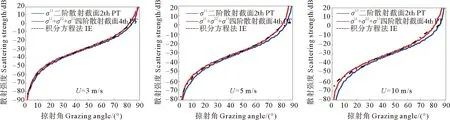
图4 不同风速小粗糙微扰近似与积分方程法比较(频率8 kHz)Fig.4 Comparison between small roughness perturbation approximation and integral equation method at different wind speeds (Frequency is 8 kHz)

对于不同频率来说，如图5所示，相同风速下，较低频率的kh值较小，更接近小粗糙微扰近似的适用条件，因此其预测准确性也较好。随着频率的增加kh值增大，二阶散射截面预测结果偏低，此时四阶散射截面仍然具有一定的准确性。

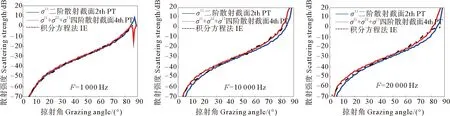
图5 不同频率小粗糙微扰近似散射强度(风速5 m/s)Fig.5 Scattering strength of small roughness perturbation approximation at different frequencies (Wind speed is 5 m/s)

图 6为小粗糙微扰近似与频率的关系，二阶散射强度几乎不随频率的变化而变化，而同一掠射角的四阶散射强度与log10f近似成正比，表1是1～25 kHz散射强度与频率线性拟合的结果，散射强度随频率变化的斜率以45°掠射角为中心呈对称变化。即靠近45°时频率依赖性最小，随着掠射角的增大或减小，频率依赖性越来越大。在20°～70°中等掠射角情况下，频率对四阶小粗糙微扰近似后向散射的影响不超过2 dB，在极小和极大掠射角情况下频率的影响会迅速增大。

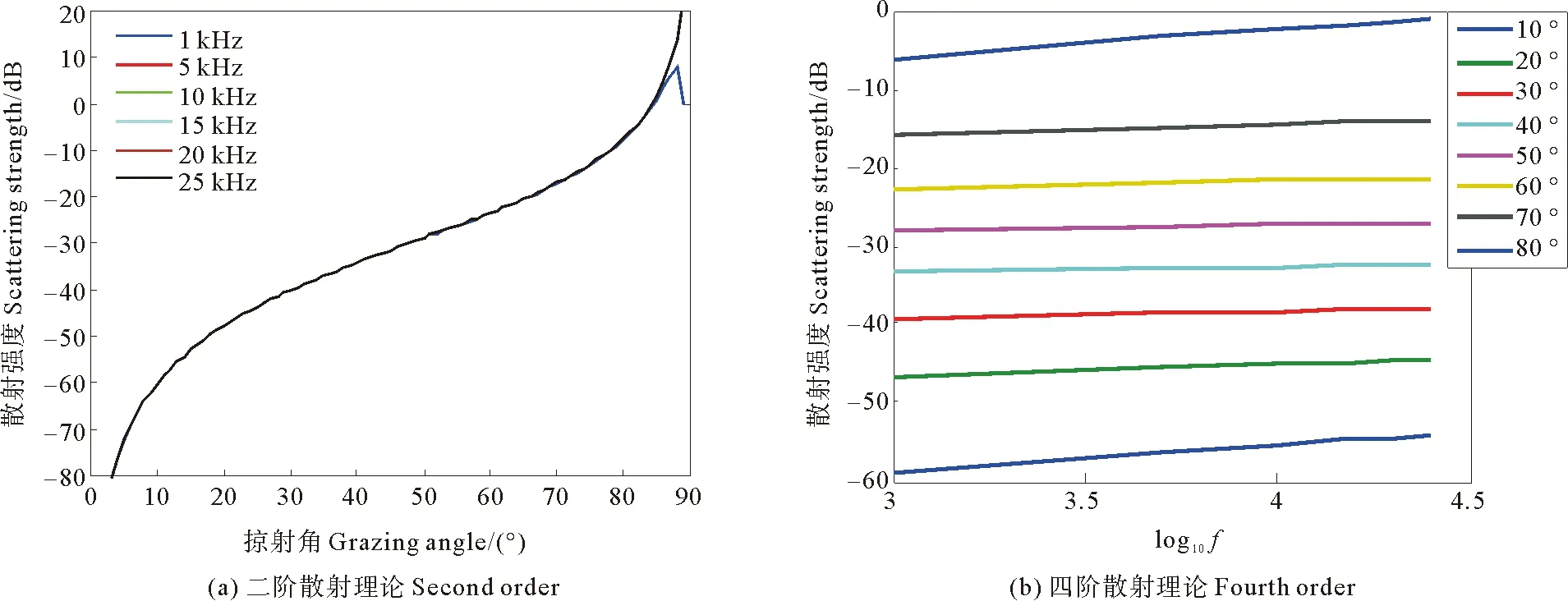
图6 小粗糙微扰近似散射强度与频率的关系Fig. 6 Dependence of perturbation approximation on frequency

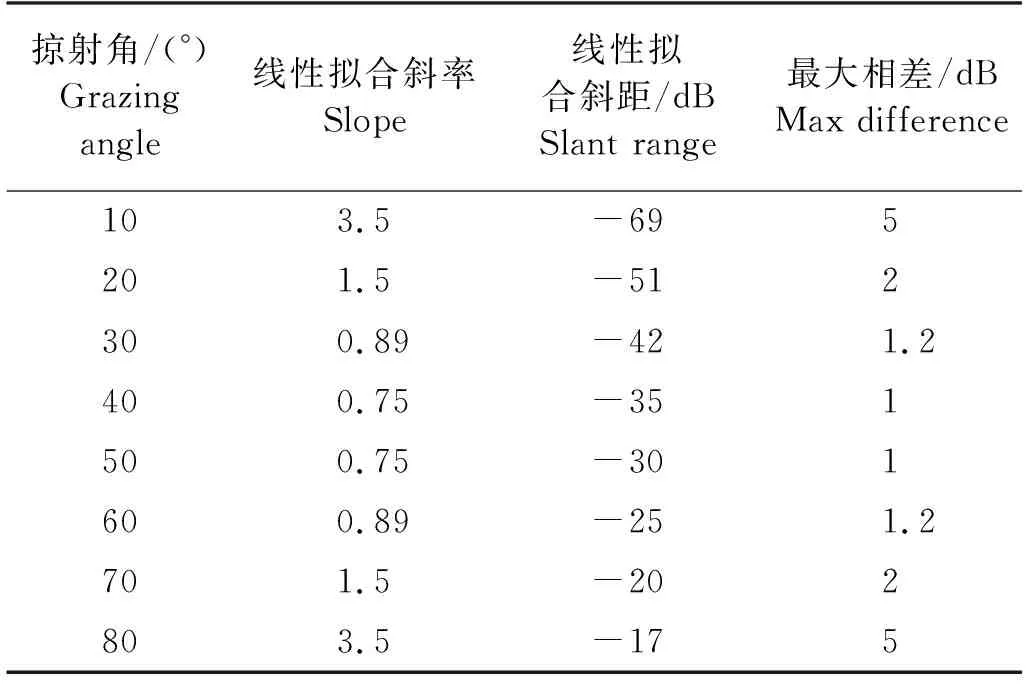
表1 四阶小粗糙微扰散射强度与log10f线性拟合结果(风速5 m/s)Table 1 Linear regression relationship between scattering strength using 4th orderperturbation approximation and log10f

此外比较中频中等风速条件下，不同粗糙散射理论后向散射预报结果(见图 7)。Kirchhoff方法只在近垂直入射时(即近镜面反射方向)准确度较高，在中小掠射角均过高的预报了海面后向散射强度。四阶粗糙微扰近似在除近垂直入射以外的所有掠射角都具有较高的准确度。小斜率近似兼具小粗糙微扰近似和Kirchhoff近似的优点，小掠射角与二阶小粗糙微扰近似一致，大掠射角与Kirchhoff近似相同，在中高掠射角的准确性最好。

图7(a)中二阶小斜率近似在掠射角大于16°时与积分方程法相差不超过2 dB，四阶微扰近似在3°～80°掠射角范围误差小于2 dB。在频率15 kHz 风速10 m/s条件下，二阶小斜率近似与积分方程法相差小于2 dB的范围缩小至掠射角大于24°。而对应四阶小粗糙微扰近似的掠射角范围约为9°～64°，64°～77°范围内的误差超过2 dB但小于4 dB，80°掠射角以上的计算误差则迅速增大。

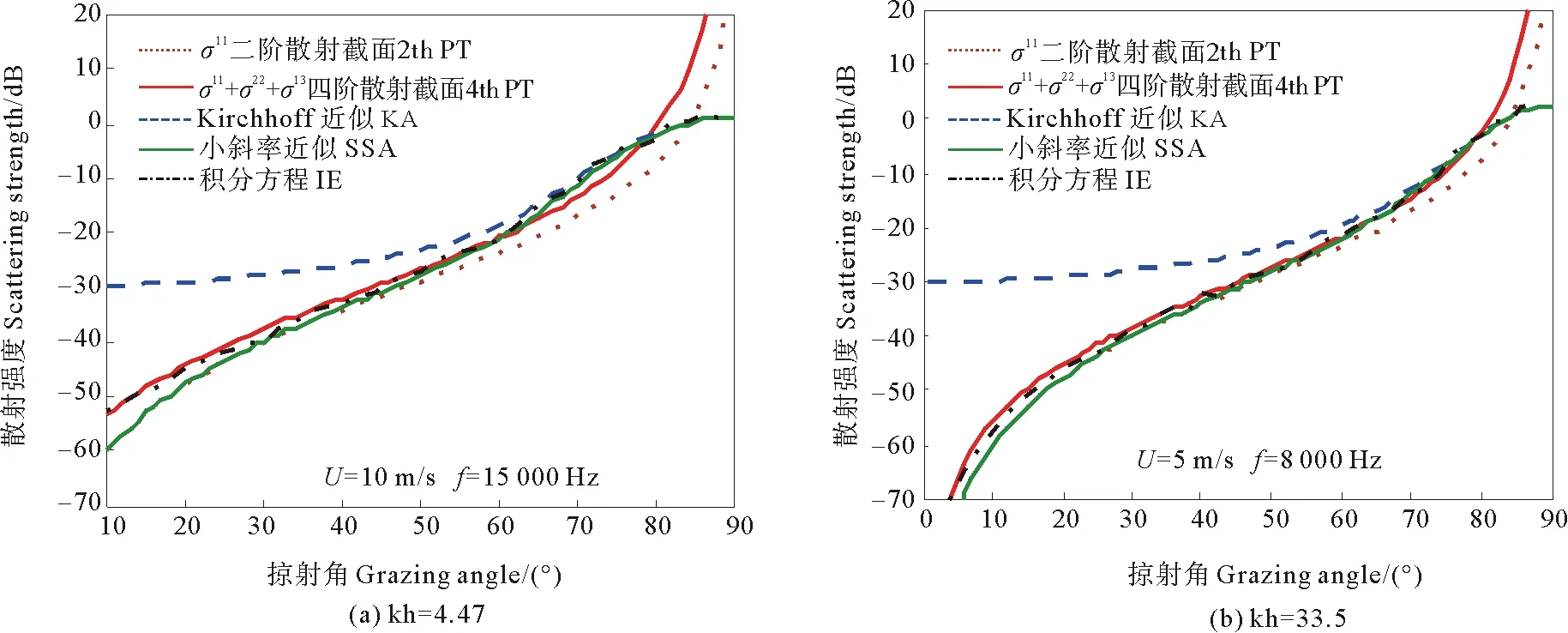
图 7 不同粗糙散射理论比较Fig. 7 Comparison between different roughness scattering theories

图8为采用全向性换能器测量实际海面后向散射强度与不同粗糙散射理论的对比结果，测量时平均风速为4.5 m/s。需要注意的是上述理论分析是在一维粗糙面条件下进行的，而实际海面是二维粗糙面。根据Thorsos的研究，在不同海浪方向性条件下二维散射强度比一维散射强度偏低5～8 dB[9]。假设海面起伏是各向同性的，那么近似有：

(26)

此时二维比一维粗糙散射小约8 dB。在图8中可以看到在中高掠射角(9 kHz为30°～80°，17 kHz为45°～80°)，实验结果与小斜率近似和积分方程法一致性较好。二阶小粗糙微扰近似只在45°掠射角附近有较好的预测准确性，其余角度的预测结果偏低。当计算至四阶粗糙微扰近似时，预测准确性有明显的提高。在近垂直入射时(80°掠射角以上)，小粗糙微扰近似明显偏高。在小掠射角范围，实验测量结果明显比理论预测值偏高，这是因为小掠射角海面散射受到气泡散射的影响，导致总散射强度远超粗糙散射理论的预测结果。

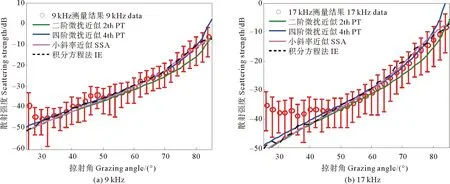
图8 测量结果与理论模型比较(风速4.5 m/s)Fig. 8 Comparison between theoretical model and measured results(Wind speed is 4.5 m/s.)

4 结语

本文利用积分方程法对Kirchhoff近似、小粗糙微扰近似和小斜率近似等方法在中频频段的有效性进行了研究，并利用实测结果对理论预测进行了验证。研究结果表明：1～20 kHz中频范围内非相干散射远高于相干散射，平均高约20 dB。在15 kHz风速小于10 m/s的情况下，24°掠射角以上小斜率近似和9°～64°掠射角四阶小粗糙微扰近似的预测误差不超过2 dB，而二阶微扰近似的预测结果明显偏低。在近垂直入射方向(80°以上)，小粗糙微扰近似过高的预报了海面散射强度，小掠射角时四阶小粗糙近似的准确性更好。Kirchhoff近似则只在近垂直入射时有较好的精度，其余掠射角的结果偏高。在实际应用中可以根据具体的掠射角范围以及频率和风速等条件选择使用适当的粗糙散射方法。同时，由于海面散射强度是统计平均的概念，只有获得足够多的测量样本，测量结果才会相对稳定。而且受测量误差、系统误差及计算误差等的影响，实际测量结果的误差一般不小于2 dB。因此小斜率近似和四阶小粗糙微扰近似对于中频频段海面散射的预测具有较强的可行性。此外，考虑到实际海上情况的复杂性，海面散射还会受到波浪破碎产生气泡散射的影响，特别是在小掠射角，此时气泡等体积散射较强，实际测量结果可能会高于粗糙散射理论的预测。