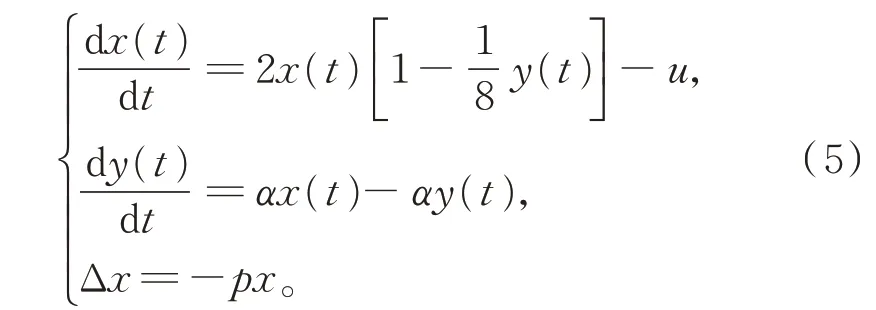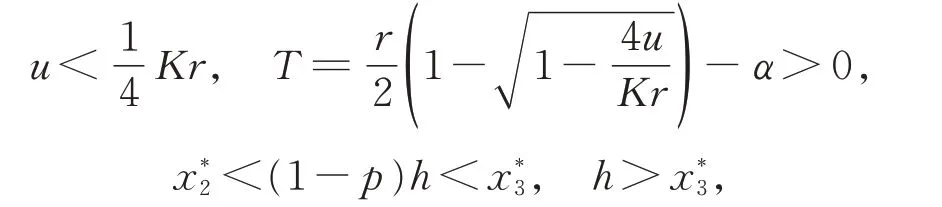一类具有分布时滞和常数收获的单种群模型的状态脉冲控制
2021-12-02李翔睿黄水波
李翔睿,黄水波
(西北民族大学数学与计算机科学学院,甘肃兰州 730030)
0 引言
脉冲微分方程是近年来微分方程研究的热点,常用于描述种群动力学行为,通过控制微分方程中的变量,实现对种群之间相互影响的控制,进而达到人们所期望的状态。1960 年,MILIMAN 等[1]提出以下脉冲微分方程:

此后,脉冲微分方程在理论上得到了进一步发展,在实践中得到了广泛应用。FU 等[2]将有界时滞量推广至无穷时滞量,并证明了具有无穷时滞的脉冲微分方程解的存在性定理,该定理促进了具有无穷时滞脉冲微分方程的发展;COOKE 等[3]研究了脉冲微分方程周期解的存在性以及极限环的存在性和稳定性;AHMAD 等[4]建立了非线性时滞微分系统解的一致稳定的判定准则,并研究了一类非线性脉冲时滞微分方程解的指数渐近稳定性,其中,具有一定收获比例的脉冲收获微分方程可实现对种群系统的最优控制,这对解决实际问题更具现实意义;WANG 等[5]提出了一种单种群模型的最优收获策略,此收获策略使得种群的收获产量达到最大或保持恒定,当收获发生在严格的时间间隔内时,种群水平达到最高;PANG 等[6]分析了具有分布时滞和状态脉冲的单种群模型:
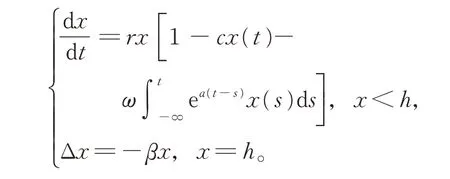
利用微分方程理论和后继函数法,得到了阶一周期解的存在性,建立了一种处理半连续系统阶一周期解的稳定性方法;LI 等[7]考虑了一类具有弱核时滞和常数收获的单种群模型:
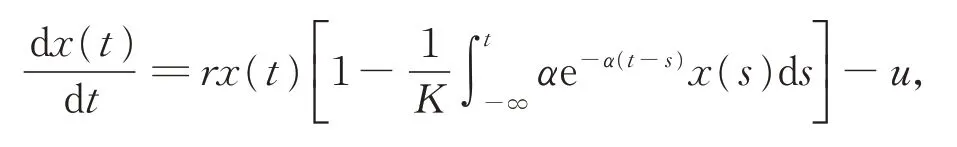
其中,x(t)为在t时刻的种群密度,r>0 为物种的内禀增长率(反映物种本身的特点),K>0 为容纳能力,αe−α(t−s)为弱核函数,u为常数收获率,α和u为正常数。
文献[7]中的模型通过
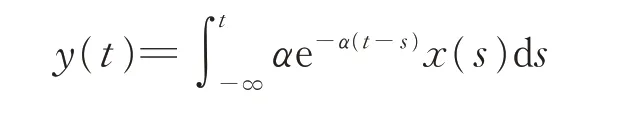
变换,得到

因式(1)在实际应用中具有局限性,本文将对变量进行状态脉冲控制。脉冲控制方程已用于生态领域中害虫的控制、经济领域中储蓄率的控制、工程领域中交通信息的控制以及航空领域中卫星轨道运行的控制等。
对式(1)中的参数x进行状态脉冲控制,得到

本文主要研究式(2)在不同情况下周期解的存在性和轨道稳定性。下文安排如下:第1 节介绍与本文相关的定义和引理,第2 节研究式(2)在给定条件下阶一周期解的存在性,第3 节讨论式(2)在阶一周期解存在情况下的轨道稳定性,第4 节通过数值模拟验证本文结论的正确性。
1 预备知识
对于脉冲系统:

设脉冲集为M,相集为N,有以下定义:
定义1[8]假设存在映射f:N→N,且 对∀P∈N,式(3)存在过点P的轨线Γ,与脉冲集M交于点P1。P1在脉冲控制方程的作用下,到达点,则称为点P的后继函数,P1为P的后继点。
定义2[9]假设式(3)存在阶一周期解Γ=f(C,t),对∀ε>0,存 在δ>0 和t0>0,使得对∀C1∈U(C,δ)∩N,当t>t0时,总有距离d(f(C1,t),Γ)<ε,则阶一周期解Γ是轨道渐近稳定的。

且足够小时,平衡E3(,)通过Hopf 分岔出现唯一稳定的极限环分岔。
引理2[9]式(3)的后继函数−l(P)是连续的。
引理3[10]若存在2 个点A,B∈N,且后继函数

则在点A和点B之间一定存在一点C∈N,使得后继函数g(C)=0。
引理4[11-12]假设脉冲系统为
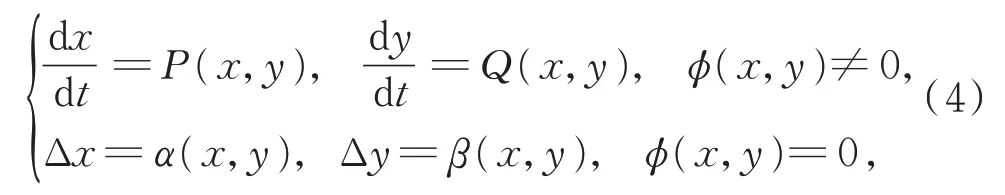
则当乘子|μ2| <1 时,式(4)的T-周期解x=ξ(t),y=η(t)的轨道是渐近稳定的。在式(4)中,

2 周期解的存在性
研究式(2)在不同参数条件下阶一周期解的存在性。

考虑脉冲系统式(2)阶一周期解的存在性。
定理1若式(2)中的u和h满足:

则存在阶一周期解。
证明当时,由引理1 可知,式(2)在无状态脉冲控制时(即式(1)),平衡点E3(,)渐近稳定、不稳定或通过Hopf 分岔出现唯一稳定的极限环分岔,其脉冲集为M:x=h,相集为N:x=(1−p)h,如图1 所示。

图1 Fig.1
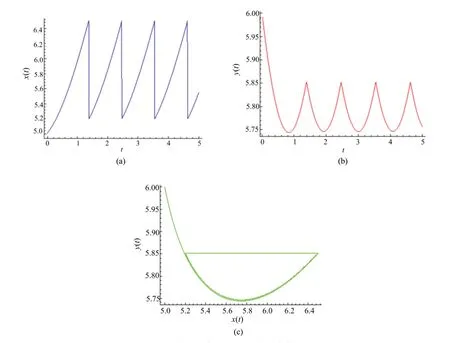
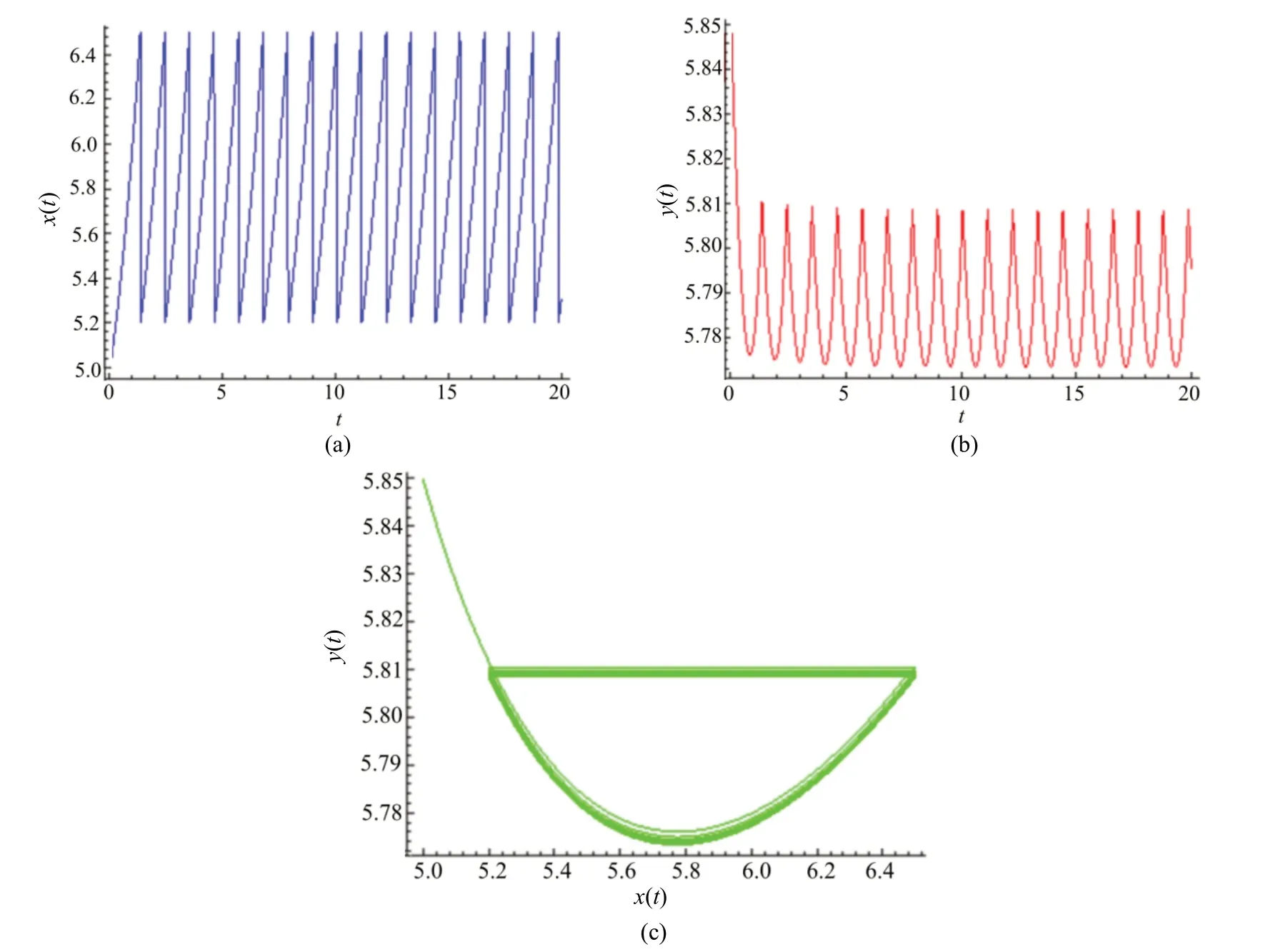
任取一点A0∈N,使得yA0>,即A0为相集N上位于平衡点E3左上方的点。从点A0出发的轨线分别与相交,到达脉冲集M:x=h上的点A1(h,yA1),随后点A1在脉冲控制的作用下,沿与x轴平行的方向最终到达相集N:x=(1−p)h上的点A2((1−p)h,yA1)。此 时,A2为 点A0的后继点,且A0的后继函数为f(A0)=yA2−yA0。又因为A2在A0的下方,即yA2 经过点A2的轨线与脉冲集M:x=h相交于点A3。在脉冲控制的作用下,脉冲函数将点A3映射到相集N:x=(1−p)h上的点A4,则A4为点A2的后继点且位于A2的上方,此时,A2的后继函数为f(A2)=yA4−yA2,且f(A2)>0。因为f(A0)<0,f(A2)>0,所以f(A0)f(A2)<0,则可由引理2 和引理3 得,在A0和A2之间一定存在一点C,使得f(C)=0。因此,当 时,脉冲系统式(2)有阶一周期解。 证毕。时,E3(,)稳定,式(1)的轨线方向沿逆时针方向由外向内运动,其轨道已渐近稳定。所以,仅讨论当 时,E3(,)不稳定的情况,此时式(1)的轨线方向沿逆时针方向由内向外运动。 定理2若式(2)中的u,T和h满足: 则系统存在阶一周期解。 证明当 时,式(1)的平衡点E3(,)不稳定。在式(2)中,其脉冲集为M:x=h,其相集为N:x=(1−p)h,如图2 所示。 图2 <(1−p)h< 且h>Fig.2 <(1−p)h< and h> 任取一点F0((1−p)h,yF0),且yF0>yE3,则定有一条轨线从F0出发,与相交后,到达脉冲集M:x=h上的点F1(h,yF1)。随后,点F1在脉冲控制的作用下,到达相集N:x=(1−p)h上的点F2,且F1与F2的纵坐标值相同。因此,点F2为F0的后继点且后继函数f(F0)=yF2−yF0,又因为F2在F0的下方,所以f(F0)<0。 如图2 所示,定有一条轨线经过点F2与脉冲集M:x=h相交于点F3(h,yF3)。随后,脉冲函数又将点F3映射到相集N:x=(1−p)h上的点F4,F4为点F2的后继点,则F2的后继函数为f(F2)=yF4−yF2,又因为F4位于F2的上方,则f(F2)>0。 因为f(F0)f(F2)<0,所以由引理2 和引理3可得,在F0和F2之间一定存在一点H,使得f(H)=0。因此,当 时,式(2)有阶一周期解。证毕。 在式(2)中,设其T-周期解(ξ(t),η(t))通过点W+((1−p)h,η0)∈N,W(h,η0)∈M。由引理4,计算乘子μ2。考虑式(2)的记号,有 最终,计算乘子μ2: 由引理4 可知,当乘子|μ2| <1 时,脉冲系统的T-周期解的轨道是渐近稳定的,则有以下定理。 定理3若式(2)存在阶一周期解,当 则式(2)阶一周期解的轨道是渐近稳定的。 令r=2,K=8,则式(2)可改写为 对于定理1,u和h满足: 令α=0.6,u=2,h=6.5,p=0.2,此时的平衡点E3(,)是渐近稳定的,设初始值为(5,6),分别得到x(t)的时间序列图、y(t)的时间序列图以及x(t)和y(t)的相位图,如图3 所示。 图3 定理1 中E3(,)渐近稳定Fig.3 E3(,)is asymptotic stability in theorem 1 令α=0.2,u=2,h=6.5,p=0.2,此时的平衡点E3(,)是不稳定的,设初始值为(5,5.85),分别得到x(t)的时间序列图、y(t)的时间序列图以及x(t)和y(t)的相位图,如图4 所示。 图4 定理1 中E3(,)不稳定Fig.4 E3(,)is unstable in theorem 1 令α=0.292 8,u=2,h=6.5,p=0.2,此时的平衡点E3(,)通过Hopf 分岔出现唯一稳定的极限环分岔,设初始值为(5,5.85),分别得到x(t)的时间序列图、y(t)的时间序列图以及x(t)和y(t)的相位图,如图5 所示。 图5 定理1 中E3(,)通过Hopf 分岔出现唯一稳定的极限环分岔Fig.5 A unique and stable limit cycle bifurcation emerges via the Hopf bifurcation from the equilibrium E3(,) in theorem 1 对于定理2,u、T和h分别满足:只考虑平衡点E3(,)的不稳定情况。令α=0.25,u=2,h=7,p=0.2,设初始值为(5.5,6.2),分别得到x(t)的时间序列图、y(t)的时间序列图以及x(t)和y(t)的相位图,如图6 所示。 图6 定理2 中E3(,)不稳定Fig.6 E3(,)is unstable in theorem 2 由图3~图5 可知,数值模拟的结果验证了定理1 及定理3 的正确性;由图6 可知,数值模拟的结果验证了定理2 及定理3 的正确性。

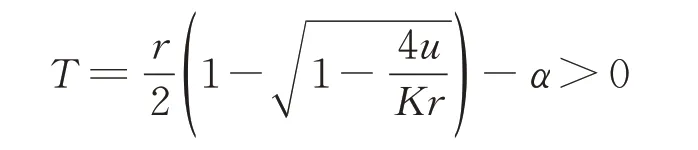
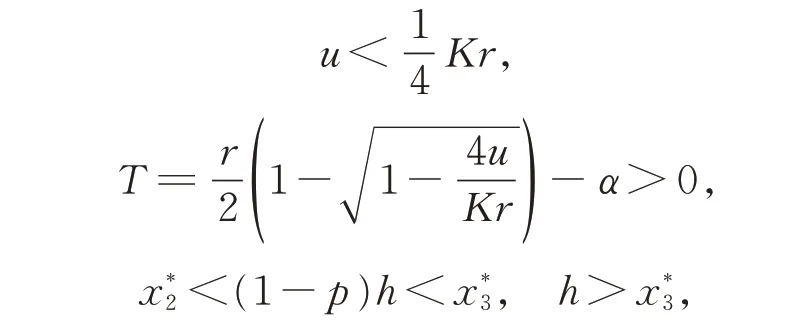



3 T-周期解的轨道稳定性




4 数值模拟