一类菌群反应扩散模型斑图的传播方式

夏 鹏，王 珍，李 旭

(1.江苏联合职业技术学院 无锡旅游商贸分院，江苏 无锡 214045；2.云南民族大学 数学与计算机科学学院，云南 昆明 650500；3.浙江理工大学 科技与艺术学院，浙江 绍兴 312369)

20世纪中叶，英国著名数学家Turing[1]首次通过生物模型解释了自然界中动物表面产生图案的原因，比如：斑马、蝴蝶等.从数学的角度上来说，这是由于生物模型中的扩散项或者趋化项会使平衡态失去稳定，从而产生图案.

最近，Tailleur[2]提出除了扩散项和趋化项能导致图灵斑图的产生，带有密度抑制运动效应的生物系统通过“自我捕获”也能产生斑图，而后Liu和Fu[3]等通过生物实验建立了带有密度抑制运动效应的数学模型.当运动函数是分段函数时，Simith-Roberge[4]等构造出了这个模型的非常数定态解以及Hopf分支.Jin[5]等改进了运动函数的条件，研究了二维平面上古典解的全局存在性以及常数定态解稳定性.Wang[6]在三维平面上研究了古典解的全局存在性.当Logistic增长率为0时，Yoon[7]对于具体运动函数，研究了任意维空间上古典解的全局存在性.Xia[8]等研究了模型的亚稳性结构.而这些研究都未涉及对于具体运动函数，该模型的斑图是通过何种方式进行传播的？

根据文献[9]中对趋化模型斑图的研究思路，本文在一维空间上拟采用相似的方法对一类菌群反应扩散模型斑图的存在性与传播方式进行探究，从而获得Ginzburg-Landau(GL) 型振幅方程，最后，通过数值仿真研究验证了初始扰动产生的斑图是通过波前方式在大区域中传播.

1 准备工作

1.1 模型介绍

下面考虑具有密度抑制运动效应反应扩散模型[10]

(1)

模型中p(x,t)和s(x,t)分别表示大肠杆菌细胞和化学信号物质酰基高丝氨酸内酯(AHL)在位置x和时间t时刻的密度；正常数γ和d分别表示Logistic增长率和AHL的扩散速率，而大肠杆菌的扩散速率依赖于运动函数eμ(1-s),μ>0.Ω=(0，l)，l是正实数.设模型满足诺依曼边界条件

(2)

以及初始条件

p(x,0)=p0(x),s(x,0)=s0(x),

(3)

ν表示在边界∂Ω向外的单位向量.

1.2 斑图的存在性

引理1[11]在一维空间Ω上，带有齐次诺依曼边界条件的-Δ算子的特征值和特征函数满足：

(4)

通过简单计算，系统(1)～(3)有2个常数解(0,0)和(1,1).在(0,0)和(1,1)处对系统进行线性化，发现(0,0)总是不稳定的，考虑到本模型是实际生物模型，不存在2种物质密度同时存在为0的情况，所以对于(0,0)情况不考虑.以下只针对常数定态解为(1,1)时研究.接下来，在(1,1)处线性化，设ωi是线性化特征值，可以得到(1,1)处的线性化特征方程为

ωi+[(1+d)λi+1+γ]ωi+(γ+λi)(1+dλi)-μλi=0,i=0,1,2,….

(5)

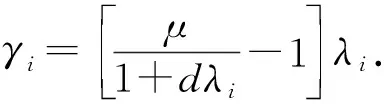
(6)

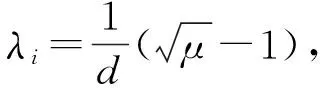
(7)

(8)

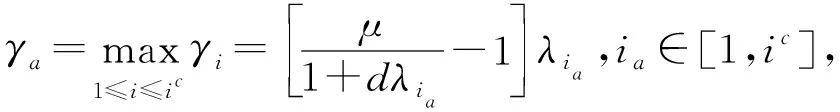
(9)

其中，ic对所有i∈[1,ic]都有γi>0成立，对所有γic+j≤0,j=1,2,….

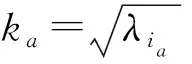
定理1假设ic满足上述陈述，那么有以下陈述成立

a.当γ≥γc时，定态解(1,1)是线性稳定的，此时不会产生斑图；

b.当0<γ<γa时，定态解(1,1)线性不稳定，即会产生斑图.

2 斑图的振幅方程

本节将应用弱非线性分析推导出描述斑图振幅的Ginzburg-Landau 方程，考虑解对空间的依赖性，引入X作为慢变量，x作为快变量，由于斑图解是从在常数定态解(1,1)附近分支出来的，因此做下列变换

P=p-1,S=s-1,

(10)

(11)

(12)

那么空间和时间的导数为

(13)

其中ε≪1.γ和E=(P,S)T幂级数展开为

(14)

其中γa在(9)式已经定义过了，Ei=(E1i,E2i)T，T表示向量的转置.将(14)式代入(11)式将相同阶数写在一起有

Λ(γa)E1=0,…o(ε),
Λ(γa)E2=D(E1),…o(ε2),
Λ(γa)E3=H(E1,E2),…o(ε3),

(15)

其中

(16)

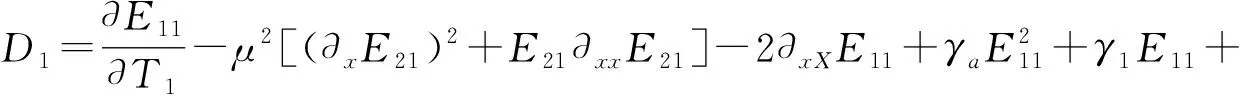
接下来利用(13)式的运算法则将(14)式代入边界条件(2)式中，得到了在x=0,l处条件为

(17)

那么结合边界条件(17)式，齐次线性系统(15)的第1个式子解为

(18)

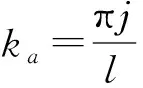
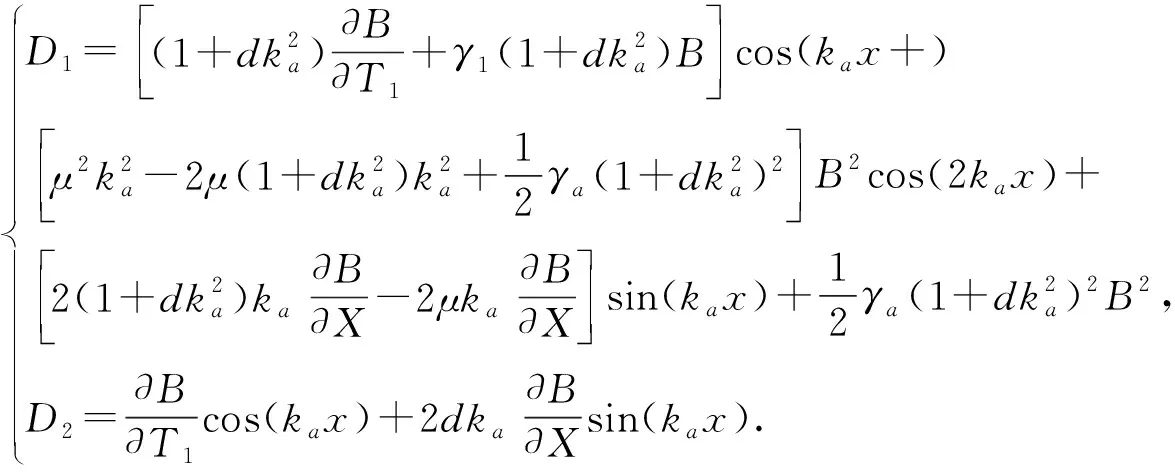
通过简单计算(15)第1个式子的伴随方程解的形式为

(19)

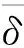
(20)

其中eij(i=1,2,j=1,2,3)分别满足下列方程

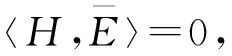
(21)

那么(21)式是经典Ginzburg-Landu 方程.应用“tanh”方法，可以找到(21)式的解为

(22)

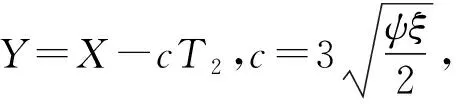
3 数值仿真

由定理1可知当γ≥γc时，系统(1)不存在斑图，当0<γ<γa时，系统(1)会产生斑图正如图1和图2所示，取γ=0.2>γc，此时没有斑图产生，当取γ=0.1<γa时，从图1中明显可以观察到有斑图产生.这恰好验证了定理1的正确性.

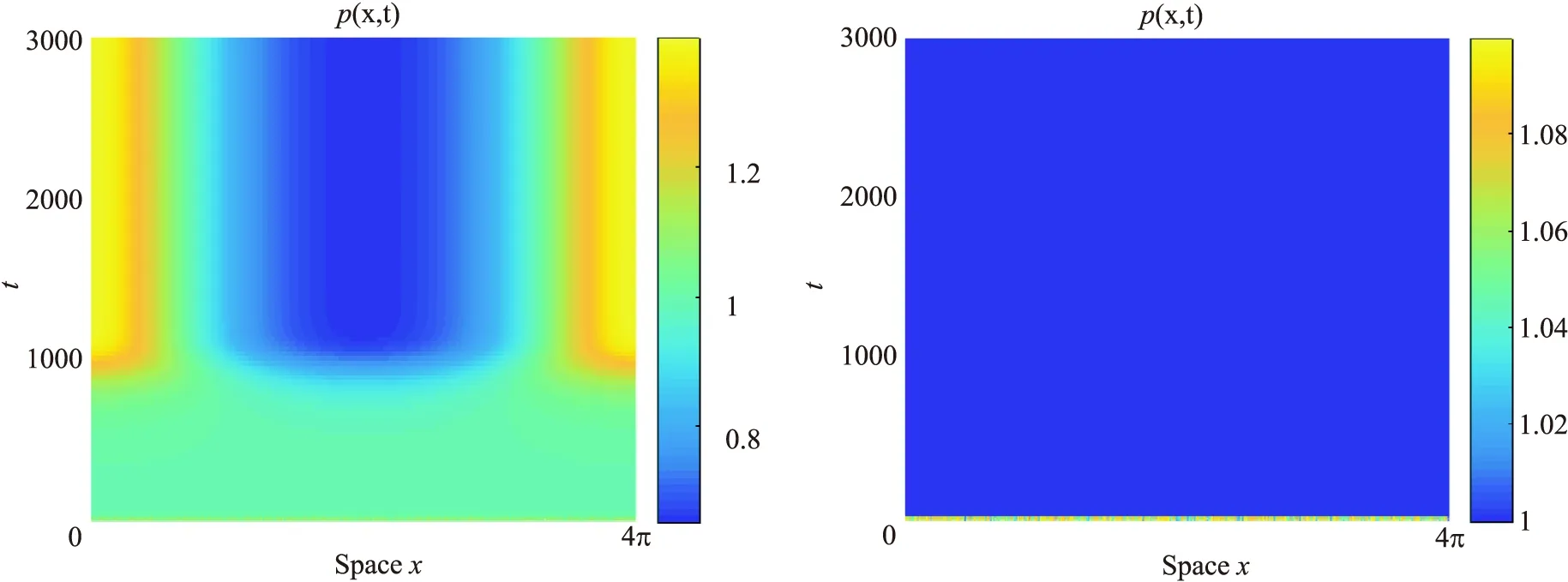
图1 γ=0.1 图2 γ=0.2

当γ=0.1时，图3展现了在大区域中，常数定态解(1,1)附近的局部扰动会通过行波的形式传播直至充满整个区域，其中黑色实线是斑图演变过程，红色虚线是振幅方程(21)的数值解.从图中可以看到振幅方程(21)很好地捕捉到了斑图通过行波演变的过程，它的二阶振幅为(0.1175,0.3067)T.这也就说明了系统(1)的斑图是通过波前来传播的.

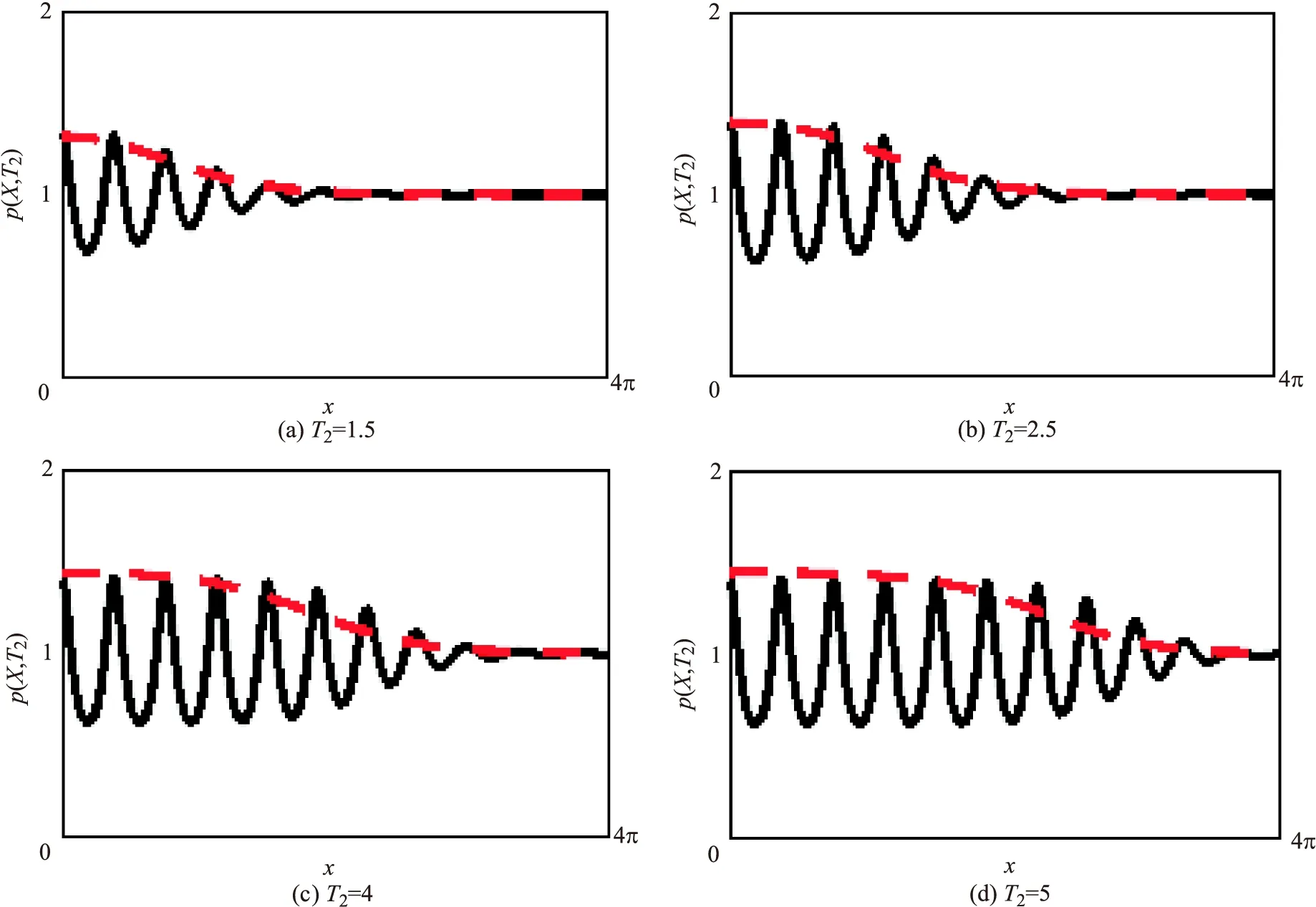
图3 黑色实线是斑图从左向右传播的过程，红色虚线是振幅方程(21)的数值解，这里γ=0.1

4 结语

文中从理论上分析了一类菌群反应扩散模型斑图存在的条件，并且通过弱非线性分析导出了GL型斑图振幅方程，这说明了该模型初始扰动产生的斑图是通过波前形式传播到整个区域.最后通过数值仿真说明了前面所得结论的正确性.