关于高阶线性复微分方程整函数解的Borel 方向

王 正， 黄志刚

（苏州科技大学 数学科学学院，江苏 苏州 215009）

1 引言及主要结果

在该文中，假定读者熟知Nevanlinna 理论以及复方程理论中的标准记号和基本内容[1-2]，下面介绍一些常用符号的定义。 设0＜α＜β＜2π，则复平面上的扇形定义为

此处n（Ω（θ-ε，θ+ε，r），f=0）表示f 在Ω（θ-ε，θ+ε，r）上零点的数量。

1919 年，Julia 由Picard 定理提出了Julia 方向的相关内容，并开始了亚纯函数奇异方向的研究，他证明了每一个超越整函数至少有一个Julia 方向。 而Valiron[3]根据Borel 定理，提出来Borel 方向的相关概念。

定义1 设f（z）是一个级为ρ 的超越亚纯函数，若对于∀ε＞0，λθ，ε（f-a）=ρ 在C∪∞上至多有两个例外值a，则称射线arg z=θ 为f 的一个Borel 方向。

自此，关于亚纯函数Borel 方向的研究在近一个世纪里迎来较大发展。2005 年，伍胜健[4]首次研究二阶线性微分方程解的Borel 方向的问题。 这类方程的一般形式为

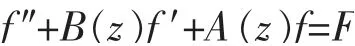
其中A（z），B（z）和F（z）都是整函数。 2015 年，黄志刚等人[5]研究了该方程的解与自由项F（z）的Borel 方向之间的关系，同时也研究了齐次方程f″+B（z）f′+A（z）f=0 的解在ρθ＝∞时的θ 集合的测度问题，下面对这些定理的内容进行简要叙述。

定理A 设A（z），B（z）为有限级整函数，F（z）为超越整函数并且max{ρ（A），ρ（B）}＜ρ（F）=∞，若arg z=θ是F 的Borel 方向，则它也是方程f″+B（z）f′+A（z）f=F 的每一个非平凡解的Borel 方向。

定理B 设A（z），B（z）为整函数且μ（A）＞ρ（B），若f（z）是方程f″+B（z）f′+A（z）f=0 的一个非平凡解，则mesI（f）≥min{2π，π/μ（A）}，其中I（f）={θ∈[0，2π）:ρθ（f）＝∞}。

文中将考虑高阶微分方程，将定理A 和定理B 推广至一般形式，并在定理B 推广形式的基础上，证明了f 的Borel 方向的测度也有类似的范围。

定理1 设A0，A1，…，An-1为有限级整函数，F（z）为超越整函数且max{ρ(A0)，ρ(A1)，…，ρ(An-1)}＜ρ（F）=∞，f（z）是方程

的一个非平凡解，若arg z=θ 是F 的Borel 方向，则它也是f 的Borel 方向。

定理2 设A0，A1，…，An-1为整函数且μ（A0）＞max{ρ（A1），ρ（A2），…，ρ（An）}，若f（z）是方程

的一个非平凡解，则mesM（f）≥min{2π，π/μ（A）}，其中M（f）为f 的Borel 方向集合。

2 预备知识

在文中，角域上的Nevanlinna 特征函数是一个很重要的工具。 若0＜β－α≤2π，k=π/（β－α），f（x）是角域Ω（α，β）上的亚纯函数，则记

其中bv＝|bv|eiβv（v=1，2，…）是f（z）在Ω（α，β，r）上的极点。

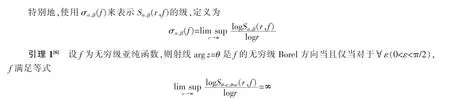
引理2[7]设f（z）为无穷级整函数，则射线arg z=θ 是f 的无穷级Borel 方向当且仅当arg z=θ 是f′的无穷级Borel 方向。

引理3[8-9]设z=rexp（iφ），r0+1＜r，α≤φ≤β，其中0＜β－α≤2π。 假设n(≥2)是一个整数，f（z）在Ω（α，β，r0）

其中E 是一个线性测度有限的集合。

3 定理1 的证明

显然方程（1）的每个非平凡解f（z）一定满足ρ（f）=∞，设arg z=θ∈[0，2π）是F（z）的一条Borel 方向，根据引理1，对于任意充分小的ε，有

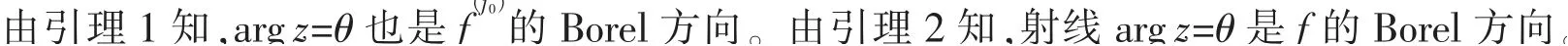
4 定理2 的证明

再根据引理6，有

由引理5 知，log+M（r，Ω（θ，ε），f）≤O（rd+k），所以ρθ（f）＜∞，与条件矛盾，故若ρθ（f）＝∞，则arg z=θ 为f 的Borel方向。

设M（f）为f 的Borel 方向集合，显然对于∀θ∈I（f），有θ∈M（f），由式（12）知，

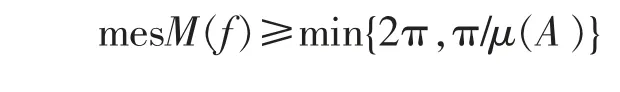
故定理2 获证。

5 结语

该文主要研究的是高阶线性微分方程整函数解的Borel 方向的问题，得到了一些相关结果，如一类方程的自由项与函数解的Borel 方向之间的关系，以及一类方程解的Borel 方向集合的测度的下界。 在此研究基础上，可开展更广泛的研究工作，如非齐次微分方程的自由项为有穷级时，它与函数解的Borel 方向之间的关系，以及自由项的Borel 方向与函数解的其他奇异方向之间的关系等。