拓展的灰色GM（1，1）模型及其应用

李嘉诺， 程毛林

（苏州科技大学 数学科学学院，江苏 苏州 215009）

如今随着时代和科学技术的发展，信息化时代如约而至，信息的变化也是日新月异。 通过对现有的信息数据进行分析模拟可以有效的对未来的发展趋势做出推测和预估。 目前研究者使用到的统计预测模型有很多，比如多元线性回归、时间序列预测等。 在1982 年3 月，我国学者邓聚龙教授在国际上首先提出了灰色系统理论，该系统理论不需要大量的样本，样本也不需要规律性分布，预测准确度高。 由于其显著的优点，从此至今，灰色系统理论被广泛应用于经济预测、能源预测、环境评估等多个方面。

灰色GM（1，1）模型作为灰色系统理论的最重要的模型之一，受到无数人的推崇。 近年来，有越来越多的专家学者对GM（1，1）模型进行研究和优化改进。 其中，徐进军等人提出了一种新的基于一次累加序列约束和基于原始序列约束条件下积分参数的确定方法[1]；徐华锋等人将灰色作用量b 改进为动态的b1+b2k 从而优化了GM（1，1）模型[2]；何文章等人运用线性规划来代替最小二乘法对模型参数进行了求解[3]；刘斌等人利用最小二乘法确定白化权函数的时间响应函数中的常数C，来构建GM（1，1）的时间响应函数的最优模型[4]；罗党等人通过用指数数列对x（1）的邻值生成数z（1）k 进行替换来达到对GM（1，1）模型的优化，并且使模型在短期、中期及长期预测中扩大了适用范围[5]；彭正明等人用积分优化、二次拟合优化等优化方法分步对GM（1，1）模型进行了改进[6]；卢懿等人通过加入调节因子λ 来优化背景值的公式[7]；杨华龙等人使用自动寻优定权对背景值进行选择，并且基于最小二乘法原理对GM（1，1）模型的初始值进行改进[8]；许秀莉等人用序列算子和影响因子对原始序列的数据进行一定的处理，提高了GM（1，1）模型的精度[9]；原玉昌等人对背景值重构和用等维递补原理对GM（1，1）模型进行改进，建立了等维递补模型[10]；豆红磊等人用Lagrange 插值法对原始序列进行修正，然后用修正后的数据建立GM（1，1）模型，改善了误差和遗漏数据导致预测精度低、残差大等问题[11]；邱利军等人通过对原始数据进行函数ln（x（0）（i）+c）变换使建模数据序列光滑度提高，进而提高所建模型的预测精度[12]；张振超等人通过引入线性时间项的灰色作用量和广义加权构造最优背景值相结合的方法，构建了优化背景值的GM（1，1）模型从而减少了预测的偏差[13]；袁磊等人利用残差尾段对模型进行修正，建立了精度更高的模型[14]；史国军、程毛林通过构建一个新的GM（1，1）拓展模型GM（1，1，dt）对GDP数据进行模拟和预测，结果与传统模型相比精度大大提高[15]；程毛林通过直接对时间响应函数优化并通过三和法和三点法优化函数初始值的方法大大提高了模型的精度[16]；程媛媛、周汉磊等人通过建立灰色预测模型对苏州市的ESV 进行有效的预测并且从中得到有效的结论[17]。

笔者通过借鉴其他专家学者的思想方法，通过对GM（1，1）模型的白化方程进行拓展，旨在能够更加贴合原始数据的非线性变化趋势，能够更好地提高预测精度。

1 拓展的灰色模型

1.1 传统GM（1，1）模型

传统的灰色GM（1，1）模型基本形式为

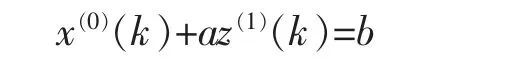
x（0）=（x（0）（1），x（0）（2），…，x（0）（n））为原始时间序列，对其进行累和则得到x（0）的AGO 生成数列x（1）=（x（1）（1），x（1）（2），…，x（1）（n）），x（1）的邻值生成数为z（1）（k）。

对应的灰色GM（1，1）模型的白化方程为

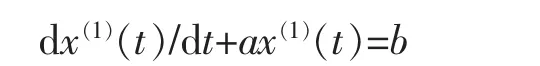
其中a 和b 分别是发展系数和灰作用量。

用求微分方程的方法可求得传统的灰色GM（1，1）模型的时间相应方程为

对其进行累减得到原始数据的预测值为

1.2 拓展的GM（1，1）模型

通过对传统模型的学习发现原始数列为指数变化且模拟和预测的精度和数据的增长速率有关。 为了缓和数据增长速率过快导致的精度变化，文中对传统灰色模型进行拓展，以此解决这类问题。设拓展的GM（1，1）灰色模型基本形式为

称其为拓展模型2。

1.3 拓展的GM（1，1）模型的时间响应方程

拓展的灰色模型的白化方程为

1.4 修正的GM（1，1）模型的参数估计

2 应用实例

第三产业增加值能够直观的反应科技、信息、金融三大行业的发展水平，因此，预测并分析第三产业增加值对我国快速发展有着重要的意义。 文中选取了2000 到2019 年这20 年间中国第三产业增加值的数据（所有数据都来自于国家统计局的《中国统计年鉴》）为基础来进行实例说明。 以2000 年到2016 年这17 年间的数据进行拟合，以2017 年到2019 年这3 年的数据进行预测。 中国第三产业增加值的实际值记为x（0）（t）（单位：亿元），有关资料见表1。

若建立传统灰色模型GM（1，1），计算得

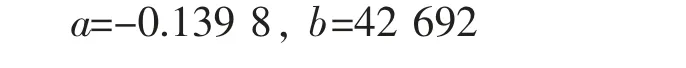
由a，b 传统模型的时间响应方程得

由x^（0）（t）=x^（1）（t）-x^（1）（t-1）计算出原始序列的模拟值和预测值，见表1。 各期相对误差和平均相对误差见表1。

若建立拓展模型1，计算得

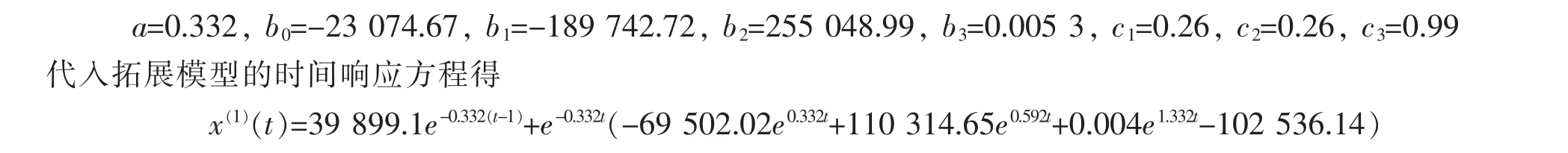
由x^（0）（t）=x^（1）（t）-x^（1）（t-1）计算出原始序列的模拟值和预测值，见表1。 各期相对误差和平均相对误差见表1。

表1 中国第三产业增加值数据以及有关计算结果

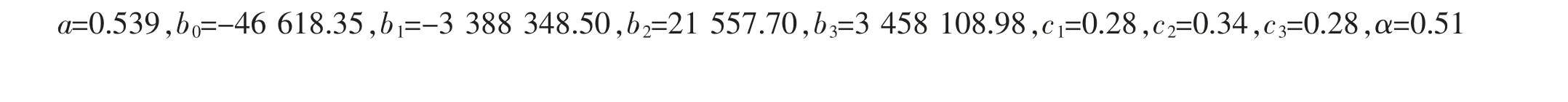
若建立拓展模型2，计算得代入拓展模型的时间响应方程得

由x^（0）（t）=x^（1）（t）-x^（1）（t-1）计算出原始序列的模拟值和预测值，见表2。 各期相对误差和平均相对误差见表2。

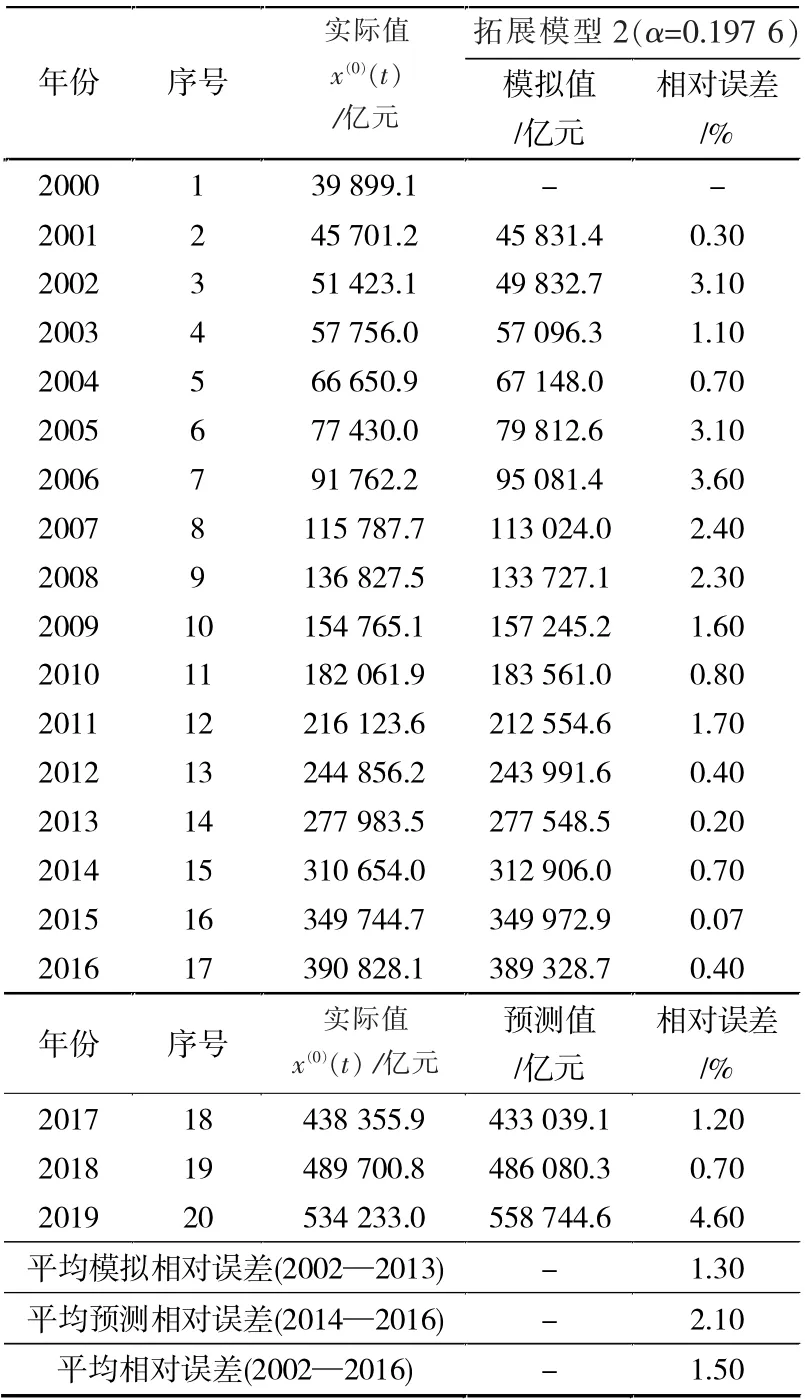
表2 拓展模型2 有关计算结果

为了更好的比较各模型误差，对各模型的拟合误差、预测误差、平均误差作直方图，如图1 所示。

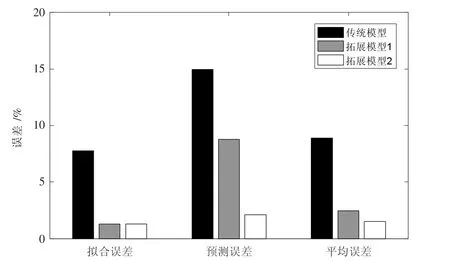
图1 三种模型的误差对比直方图

从图1 可以看出，文中给出的2 种拓展模型的平均模拟相对误差、平均预测相对误差和平均相对误差相比于传统模型来说明显减小，精度明显提高，表明文中给出的建模方法有很高的可靠性和有效性，可以适用于第三产业增加值的相对预测。 相比较而言拓展模型2 的精度最高。

3 结语

笔者对GM（1，1）模型做了简单的介绍，通过传统的GM（1，1）模型引申出其拓展模型GM（1，1，beck）。 同时文中给出等权和不等权拓展模型的白化方程、灰微分方程、时间响应方程的公式并且给出估算参数的方法。通过对2000 到2019 年的中国第三产业增加值数据进行模拟和预测，由数据显示发现等权的拓展模型和不等权的拓展模型相比于传统的GM（1，1）模型来说，在对第三产业增加值这个数据的模拟和预测方面的精度都有很大的提高，再对两者进行比较发现，不等权的GM（1，1，beck）模型的精度最高。 通过用不等权的GM（1，1，beck）模型对2020、2021 年中国第三产业增加值进行预测得到670 599.42 亿元和856 876.06 亿元这两组数据。 尽管文中涉及的不等权的GM（1，1，beck）模型预测精度比传统GM（1，1）模型高，但仍然存在着一些问题，比如此拓展模型不一定适应所有的数据，再者文中的误差还有提高的可能，可以通过优化背景值的方法来进一步降低预测的误差，这也是未来的一个研究方向。