静电负刚度谐振式加速度计的非线性振动特性研究

2021-12-02吴天豪

导航定位与授时 2021年6期

吴天豪，张晶，苏岩

(南京理工大学机械工程学院，南京 210096)

0 引言

20世纪70年代，Roylance研究团队发表了有关微加速度计的文章。时至今日，微机电系统(Micro-Elec-tro-Mechanical System，MEMS)加速度计已经发展了近半个世纪。随着应用范围的拓宽，MEMS加速度计也从最早的军事、航空航天领域[1-3]，慢慢延伸到了电子器件、定位导航和医疗设备等领域[4-5]。其中基于静电负刚度敏感原理的静电负刚度谐振式加速度计(Electrostatic Negative Stiffness Resonant Accelerometer，ENSRA)受到广泛关注。由于其本质为频率调制的电容式MEMS加速度计，使得ENSRA一方面避免了电容式MEMS加速度计因电路噪声导致零偏稳定性较差的问题,另一方面也规避了振梁式MEMS加速度计受残余应力影响而产生谐振频率误差的问题。在目前已报道的静电负刚度加速度计中，首尔大学研究团队在2004年报道了一种面内静电负刚度加速度计，灵敏度为128Hz/g,相对灵敏度为5470×10-6[6]；并在2005年报道了一种面外静电负刚度加速度计，灵敏度为70Hz/g，相对灵敏度为5833×10-6[7]。2013年，美国加利福尼亚大学欧文分校A.M.Shkel团队报道了一种灵敏度为4.4Hz/g的加速度计，实现了大于3×105的品质因数和6μg的零偏稳定性[8]。除此之外，中国的清华大学、东南大学和南京理工大学等研究团队也在此方向做了相关研究[9-10]。随着应用领域的不断拓宽，对于MEMS加速度计性能的要求日益提高，研究者们往往通过加入静电力来软化机械刚度，从而提高灵敏度等关键指标[11-12]。但是随着静电力的增大和器件灵敏度的提高，非线性振动效应却愈加明显，反而制约着整体性能的进一步提升。

本文以ENSRA作为研究对象，探究机电耦合下敏感结构的动力学振动模型，分析了高阶非线性刚度的产生原理，并结合实验结果探讨了静电力与非线性振动的一般关系，最终给出了优化方案。

1 ENSRA非线性振动模型

1.1 静电负刚度的形成及动力学原理

基于静电负刚度调谐的谐振式加速度计其本质是频率检测的电容式MEMS加速度计，利用平板电容产生的静电力作用在敏感结构的质量块上而产生等效负刚度的原理来改变振动的谐振频率。不仅如此，ENSRA非线性振动的本质也是平板电容产生的静电力导致的，所以讨论静电负刚度的原理及其应用到ENSRA中的影响是至关重要的。

本文研究的基于ENSRA的敏感结构由上、下2个谐振器组成，如图1[10]所示。

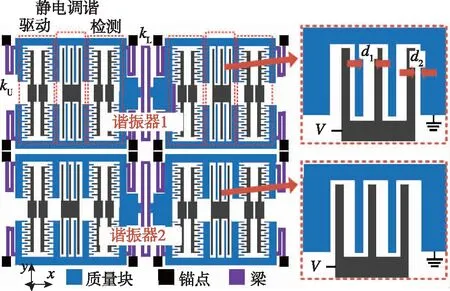
图1 ENSRA敏感结构结构示意图Fig.1 Schematic diagram of ENSRA sensitive structure

每个质量块由4个U型梁和锚点相连接，同一个谐振器的2个质量块由4个L型梁相连。每一个质量块内部分为三部分，分别是差分梳齿驱动电容、静电调谐的变间距平板电容和差分梳齿检测电容，质量块中间黑色部分为固定极板。静电调谐的变间距平板电容中，大间距为d1，小间距为d2，上下2个谐振器平板电容所放置的位置相反。也就是说，当外界输入加速度时，整个敏感结构的质量块向一个方向移动，但是一个谐振器的平板电容极板间距变大，另一个极板间距变小，使得上下2个谐振器的谐振频率一个变大一个变小，最后通过频差计算较精确的谐振频率。

在ENSRA工作时，敏感结构中差分梳齿驱动电容决定了每个谐振器的工作模态，分别有同向工作模态和反向工作模态，图2所示为一个谐振器在ANSYS下的模态仿真。其中，反向工作模态是运行模态，当外界输入加速度时，每个谐振器的2个质量块沿中线镜像反方向振动，在此工作模态下，通过电路设计达到谐振频率下的稳定状态；同向工作模态为检测模态，当敏感结构稳定时，改变差分梳齿驱动电容的电压，使得2个质量块同向振动，再由差分梳齿检测电容检测谐振器的谐振频率。

1.2 非线性模型的推导

本文研究的是运行模态下的非线性振动问题，因此对该加速度计在反向工作模态下的敏感结构进行理论分析与仿真验证。由于上下谐振器不同的谐振频率变化对非线性的研究没有影响，因此选取敏感结构的一个谐振器作为研究对象。

在反向工作模态中，2个质量块在每一时刻的移动位移相反，在连接L型梁的对称面保持静止，使得整个谐振器的谐振频率和其中单个质量块的谐振频率相同，等效质量是单个质量块的2倍，等效刚度也是单个质量块的2倍。因此，对于非线性模型的建立，选取其中二分之一谐振器作为研究对象。

1.2.1 谐振器等效模型受力分析

以单个谐振器的二分之一为研究对象,由于质量块本身变形非常小近似刚体，一端由4个U型梁并联成等效刚度为KU的弹性约束，另一端与2个L型梁相连。在反向工作模态中，L型梁可近似看成一端固定，另一端与质量块相连，因此可等效成一个谐振梁，如图3(a)所示。当敏感结构处于工作模态时，质量块受到变间距平板电容的静电力，可建立修正后的谐振梁力学模型，如图3(b)所示。

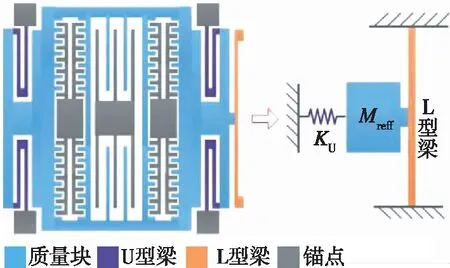
(a)ENSRA单个谐振器等效力学模型图

根据图3所示，作如下定义：

1)敏感结构的材料密度为ρ，厚度为b，谐振梁长度为L，宽度为h，横截面积为A=bh，面内弯曲的惯性矩为I=bh3/12；

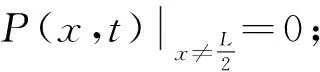
3)谐振梁振动的轴向位移为ux(x,t)，横向位移为uy(x,t)；

4)任取一微段dx，其受到轴向力F(x,t)、剪切力T(x,t)和弯矩M(x,t)。

由此可见，分析谐振器受力的关键在于静电力P、轴向力F、剪切力T和弯矩M。

首先讨论L型梁的轴向力、剪切力和弯矩，设L型谐振梁在上述作用下的弯曲应变为γ，则可得

(1)

同理可设L型谐振梁的轴向应变为η，可得

(2)

通过化简式(1)和式(2)，可求解L型谐振梁所受的弯矩和轴向力为

(3)

(4)

根据L型谐振梁的振动特性，可以将轴向力F(x,t)视作仅与时间有关的函数而忽略随空间的变化，即F(x,t)=F(t)。将式(4)从0到L积分，并且添加边界条件ux(0,t)=ux(L,t)=0，则可得到

(5)

1.2.2 变间距平板电容静电力P求解

如图1所示，对其中谐振器的二分之一进行计算，静电调谐的平板电容采用变间距电容检测方式，其电容可以表示为

(6)

式中，ε为真空介电常数；b为变间距平板电容宽度即敏感结构厚度；Ne为变间距平板电容个数；le为变间距平板电容两极板重合面长度；d1为变间距平板电容大间距，d2为变间距平板电容小间距；x为变间距平板电容移动极板位移即敏感结构位移。

可得变间距平板电容产生的静电力为

(7)

式中，V为两极板之间的电压差。

式(7)在图3中，其移动极板位移可表示为

(8)

则有

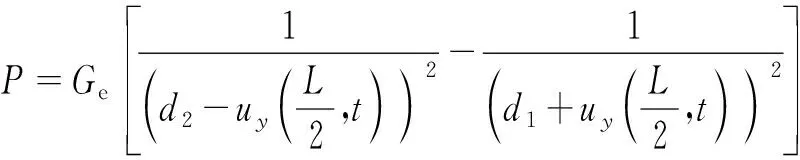
(9)

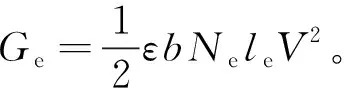
(10)

1.2.3 机电耦合的非线性动力学方程

哈密顿原理(Hamilton Principle)又称最小作用原理，通常用来建立连续质量分布和连续刚度分布系统(弹性系统)的动力学模型。设系统动能为KT，系统势能为U，系统所耗散的能量为Wc，则有耗散系统的广义哈密顿原理可表示为

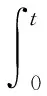
(11)

根据1.2.1节分析的该敏感结构中L型谐振梁单自由度振动的力学模型可得，该系统的动能为

KT=KL梁+KM

(12)

系统势能包括L型谐振梁的轴向应变能、弯曲应变能、U型梁弹性势能和变间距平板电容产生的静电势能，结合式(3)与式(5)，可推导L型谐振梁的势能为

U=Ubend+Uaxial+UK+Ue

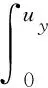
(13)

系统所消耗的能量可以表示为

(14)

(15)

式中，Фi代表双端固支梁在第i阶模态下的振型;qi为广义坐标，代表在第i阶振动模态下谐振梁随时间变化的位移。

对于本文研究的L型谐振梁，将围绕一阶模态进行研究，其振动模态如图4所示。

图4 双端固支梁一阶模态振型图Fig.4 Diagram of double end fixed beam in first-order mode

其对应的振型方程为

Φ1(x)=C1[coshβ1x-cosβ1x+

α(sinhβ1x-sinβ1x)]

(16)

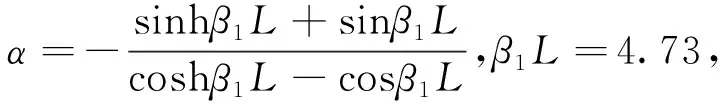
表1 双端固支谐振梁一阶模态各项参数计算

将上述能量式代入有耗散系统的广义哈密顿原理方程中，通过变分的方式，利用哈密顿原理得到广义拉格朗日方程

(17)

将式(15)代入上述能量式进行变量分离，只考虑一阶振型，共同代入式(17)，在不考虑驱动力的情况下，得到L型谐振梁横向振动的运动微分方程

(18)

将静电项泰勒展开，并省略高阶项得

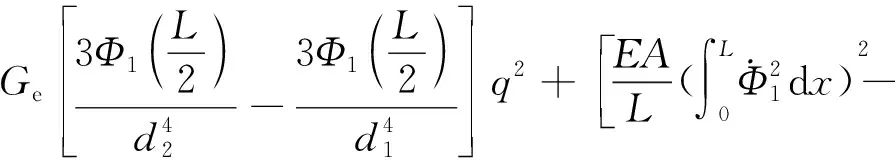
(19)

由此，可以对L型谐振梁建立机电耦合的非线性动力学方程

(20)

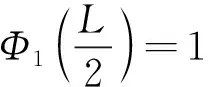
(21)

(22)

(23)

(24)

(25)

该机电耦合模型中，K1为一阶刚度项，包含机械刚度和静电力产生的静电负刚度；K2为二阶刚度项，是由静电力产生的非线性负刚度项；K3为三阶刚度项，是由L型梁轴向应变与静电力产生的三阶非线性刚度项，其中轴向应变为主要因素占比95.3%；Ce为静电力产生的恒力。

由此可见，静电力的引入对于ENSRA来说，不仅提供了敏感加速度的静电负刚度，还产生了二阶和三阶的高阶非线性刚度项，对驱动力产生一个直流偏量，使得整个敏感结构处于非线性振动状态，对后续器件的检测性能产生影响。

前文中涉及的关键结构尺寸如表2所示。

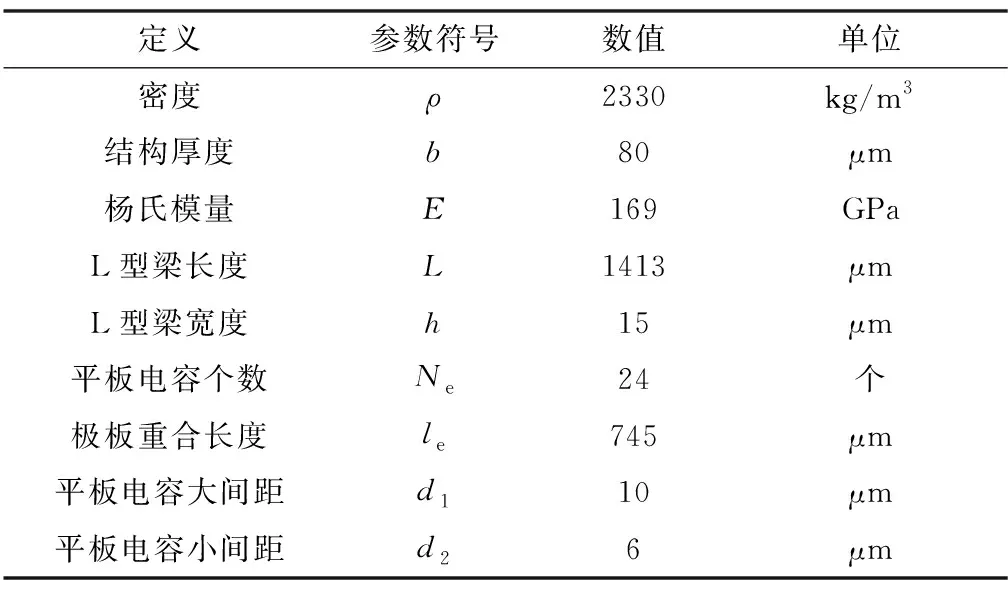
表2 ENSRA关键结构尺寸

2 实验结果

2.1 静电力对非线性振动的影响

由第1节的非线性动力学模型可知，除了L型梁轴向应变带来的部分三阶非线性刚度项之外，静电力的引入对结构的非线性振动起着决定性作用。在开环测试下，扫频结果和不同加速度下输出频差的关系如图5所示。

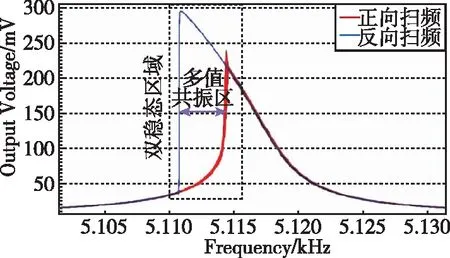
(a)ENSRA单个谐振器正反扫频实验结果

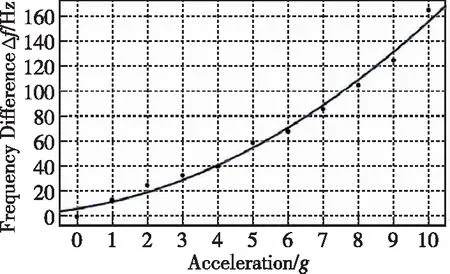
(b)0～10g下ENSRA差分输出结果图5 非线性振动试验现象Fig.5 Phenomenon of nonlinear vibration test

一方面，高阶非线性刚度项的引入使得扫频谐振峰发生左偏现象，导致谐振器频率的减小，等效为刚度软化，在器件处于低阻尼高Q值的情况下，其幅频响应曲线存在双稳态区域，谐振峰发生左偏，导致同一个谐振频率对应多个振幅出现多值共振情况，这种现象可划分出稳态区域和非稳态区域，曲线在峰值会发生跳变现象，对后续闭环电路锁定谐振频率带来困难，从而影响加速度计的正常工作；另一方面，与梳齿电容不同的是，变间距平板电容改变静电力的本质是两极板间距的变化，这种方式使得平行极板的吸附效应大大增加，因此随着输入加速度的增大，敏感结构内可移动极板向固定极板不断靠近，两极板之间的吸附效应不断上升，使得输入输出存在非线性关系，一定程度上制约了量程的设置。

2.2 非线性振动优化方案及实验验证

2.2.1 高阶非线性刚度项优化

由式(19)可知，影响高阶非线性刚度项K2和K3的关键因素为静电力、L型梁轴向应变和振动幅值，这里将多值共振区大小作为衡量非线性振动程度的指标。驱动电压决定着振动幅值的大小，当驱动力较小，振动幅值q与极板间距d1、d2相差1个数量级以上时，在非线性振动方程中高阶项可以近似被省略，所带来的非线性效应相对较小；但当驱动力增大到一定程度时，振动幅值q与极板间距d1、d2处于同一个量级，高阶项无法被忽视，非线性效应明显。而静电力的大小影响着高阶非线性刚度项，因此可通过调节驱动电压和调谐电压来一定程度上抑制非线性振动。

如图6(a)所示，随着驱动电压的减小，振动幅值相应减小，使得相较于极板间距来说，振动幅值可以忽略；高阶非线性刚度项影响因子变小，导致双稳态区域减小，多值共振区从3.84Hz降低到1.95Hz，非线性振动优化了49%。因此，通过减小驱动力的优化方案以降低幅值从而缩小多值共振区，达到优化非线性的目的。

图6(b)中，调谐电压的降低表示静电力的减小，导致以静电力为主要影响变量的高阶非线性刚度项K2减小而K3相对增大，整体振动非线性降低，谐振峰左偏程度减小，双稳态区域明显缩小，多值共振区从3.84Hz降低到2.12Hz，非线性振动优化了44%。这一方面证明了调节静电力方案的可行性，从根本上降低了二阶非线性刚度项，使得整体非线性振动效应降低；另一方面可以看出，谐振峰的左偏现象受二阶非线性刚度项的影响，二阶非线性刚度项的减小有效优化了谐振器等效刚度的软化现象。

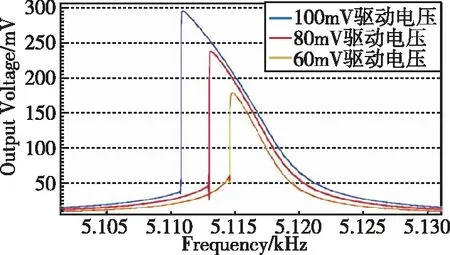
(a)不同驱动电压下ENSRA扫频结果

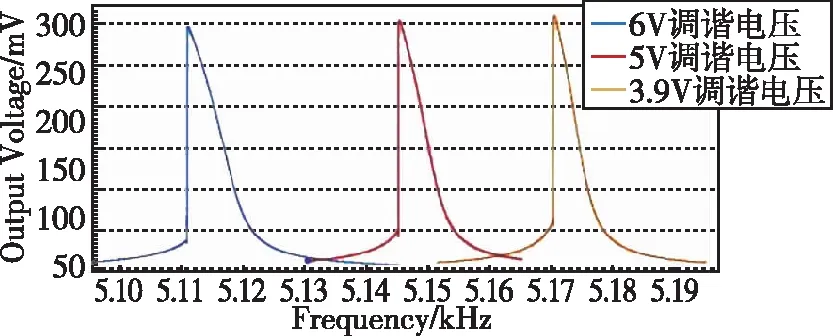
(b)不同调谐电压下ENSRA扫频结果图6 高阶非线性刚度优化实验图Fig.6 Experimental diagram of high order nonlinear stiffness optimization

2.2.2 吸附效应优化

平板电容最主要的特性在于当两极板电压差保持不变时，随着两极板间距的变化，其两端的电容也会发生变化，导致产生的静电力发生变化。但是这种变化存在一个临界值，静电力过大会使得敏感结构提前到达临界值。

由式(9)可知，决定变间距平板电容静电力大小的因素有调谐电压、极板间距和极板重合面积。实验通过控制调谐电压大小，改变敏感结构调谐部分产生的静电力，观察输入输出非线性变化情况，如图7所示。通过给变间距平板电容施加不同的调谐电压(6V，5V，3.9V)以改变两极板的电压差，在开环的情况下测试其在0～10g下的输出频差。

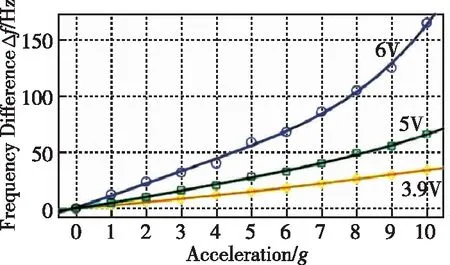
图7 不同调谐电压下的加速度-频差曲线图Fig.7 Acceleration frequency difference curves under different tuning voltages

由图7可以清晰直观地看出，随着调谐电压的减小，输出频差与输入加速度的线性度越来越高，当调谐电压从6V降低到3.9V时，输出非线性从3.4×106ppm降低到 4.95×102ppm，输出非线性优化了将近4个数量级，因此验证了调整调谐电压优化方案的可行性。这是由于当调谐电压减小时，两极板的电压差减小，在两极板间距相同的情况下静电力减小，即在相同加速度输入的情况下，调谐电压较小的平板电容可移动极板的位移较小，因此可以通过延长平板电容吸附效应的临界点，使得ENSRA的量程增长。