一种装配体模型的离散量化与相似性分析方法
2021-12-02张杰季宝宁杨宁唐文斌
张杰,季宝宁,杨宁,唐文斌,2
1. 西北工业大学 机电学院,西安 710129 2. 西安工程大学 机电工程学院,西安 710048
随着近年来计算机辅助设计(CAD)技术的不断发展,现有基于模型定义(Model Based Definition,MBD)的产品数字化研制体系中,三维模型广泛关联了产品全生命周期上、下游的相关信息,包括工艺设计、加工制造和维修/维护等各个方面,由此形成了极具实践意义的知识脉络[1-2]。在此背景下,重用这些模型及其关联的各类设计知识,如设计要求、工艺文档、仿真数据等,已经成为新产品快速研制的重要方式。为了支持工程技术人员进行设计重用,近年来,以三维CAD模型为对象的检索技术已成为人们普遍关注的热点之一。
在航空航天等制造企业中,产品设计的最终形态通常是以装配体模型的形式存在。装配体模型是众多零件模型通过多种连接及层次关联形成的系统,既能够直观描述产品的局部细节特征和整体外形,也是功能、性能、制造工艺和产品维护等各类设计意图的集中体现,因而具有极大的信息重用价值[3]。近年来众多学者以装配体模型为研究对象展开大量模型相似性分析方法等相关研究。
Deshmukh等[4]较早地给出了一个基于内容的装配体检索系统,利用配合图组织装配体所包含的零件和装配信息,并详细给出了相关的检索条件、检索算法和检索策略;Han等[5]提出了一种基于高级语义知识的装配模型设计重用方法,通过零件语义、装配约束语义和功能语义3个方面来描述装配模型。Chen等[6]提出了基于骨架的装配体模型相似性分析方法,利用多层次装配描述符对装配体进行描述;文献[7-9]也从组件几何约束、零件接触面、零件形状和统计数据等方面,利用编码等手段进行装配体信息量化等相关研究,并通过图匹配算法实现模型相似性分析。这些方法的研究重点在于零件间连接关系及工程语义类信息的量化表达,在相似性分析时普遍采用图、子图同构及频繁子图挖掘等方法,能够较为准确地识别两模型中结构相同的部分区域。但这些方法对结构的差异性较为敏感,两个装配体模型中即使存在较小的差异,如在模型中增加或删除或更改一个零件,也会对匹配结果产生较大影响,不利于装配体结构相似性的高效分析。
此外,图同构算法具有较高的时间复杂度,如何提高图搜索效率也是需要关注的重点问题。目前研究学者提出了一系列算法,如GraphGrep[10]、GIndex[11]、RWM[12]等,这些方法普遍遵循“剪枝-验证”框架:即通过离散化思想将原始图数据分割为若干个结构较为简单的“特征图”,利用“特征图”构建索引结构;然后利用索引结构对搜索空间进行匹配实现快速剪枝,并在已匹配“特征图”的聚合过程中验证图之间的相似性。实验证明这些方法较传统的图同构算法具有更好的计算效率,但这些方法的研究对象多为化学、道路交通等领域具有明确属性标签的图对象,如何将这种方法与装配体模型相似性分析问题相结合仍待进一步研究。
上述的方法主要采用定性的分析手段,其结果一般只有“完全相似”、“部分相似”和“完全不相似”几类,因此也有学者从定量的角度进行相似性分析。例如,考虑到装配体模型与其中零件模型间的组成关系,Hu等[13]以零件模型为对象建立几何信息量化方法,借助向量空间模型将装配体描述为n维向量;文献[14-16]考虑零件形状、空间位置及转动惯量等特征属性,将零件模型量化描述为特征空间中的点,进而通过离散点集的匹配实现装配体模型检索。这些方法利用向量间的距离大小作为判断模型相似性的依据。对于两个越相似的装配体模型,其特征向量间的距离越相近,因而无需复杂的图运算即可实现相似性分析。但是由于离散点集无法表达零件间的连接关系,将在一定程度上影响检索结果的准确性。例如,对于两个零件组成相同但连接关系不同的装配体模型仍被判定为完全相似,但事实上零件间装配方式的不同会对产品功能产生较大差异,而这种差异性无法在检索结果中体现。
在上述各类方法的启发下,为了将装配体连接关系信息融入离散点集的描述过程,进而利用高维向量间的距离计算实现装配体结构相似性分析,并支持索引结构的构造,本文提出了一种基于结构离散化的装配体模型信息量化和相似性分析方法。首先,通过分析零件的连接关系,采用离散化方法将装配体分割为若干个结构单元集合;在此基础上,建立结构-形状分布函数并将结构单元的形状与结构信息描述为特征向量,实现装配体模型的量化描述;最后,在特征空间中建立词袋(Bag of Word,BOW)索引结构进行结构单元特征向量间的近似近邻搜索,并通过Earth Mover Distance(EMD)算法实现装配体模型的相似性分析。
1 基于结构离散化的装配体信息量化方法
提出一种基于结构离散化的装配体模型量化描述方法,通过构建“结构单元”的分割方法与描述过程,能够将装配体模型的形状信息和连接信息统一量化表达为若干个高维向量构成的集合,进而支撑索引结构的构造和模型间相似性的分析。装配体模型量化描述过程如图1所示,可以分为以下3个步骤:构建属性连接图、结构单元离散化分割以及装配体描述符构建。

图1 装配体模型描述符构建过程Fig.1 Process of building assembly model descriptor
1.1 装配体连接图构建
装配体模型是由若干个零件构成的系统,其设计功能的实现通过各种零件特征和零件间装配连接的有机组合实现。为了准确反映装配体的本质属性,目前研究中通常采用图的形式对零件形状信息及连接信息进行表征。图结构具有旋转、缩放和平移不变性,为了便于计算分析,可将零件定义为图中的节点,零件间的连接关系定义为节点间的连接边,进而可将装配体模型表示为四元组形式的连接图:
G={V,E,Av,Ae}
(1)
式中:V={v1,v2,…,vn}为零件节点集合,vi表示装配体模型中第i个零件,n表示零件数量;E={ei,j|h(vi,vj)=1}为连接关系集合,ei,j表示第i个零件和第j个零件间存在连接关系,h(vi,vj)=1为判断零件vi,vj间存在连接关系;Av、Ae分别为描述零件形状信息和连接关系信息,接下来对这两种信息进行定义。
表面点集是三维模型的一种简化描述方法,能够反映模型的凹凸性、表面分布等外形特征,因此本文将表面点集作为零件的形状信息进行提取。零件间的连接关系根据具体特性可泛化为刚性连接(铆接、胶接、过盈配合等)和运动连接(转动副、球面副、齿轮副等)等,在装配体模型中这些连接关系通常都能表现为零件几何区域间的相互接触。因此在零件表面点集的基础上,本文将不同的连接关系统一用接触区域对应的点集进行表达。Av、Ae可表示为
(2)
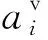
1.2 结构单元离散化分割
受文献[12]的启发,本文以连接图的各条边为对象作为装配体结构相似性分析的数据基础,并以此为基础进行索引结构的构造。在本文所构建连接图中,每条边及其关联的顶点能够表达装配体中两个零件的形状和连接信息,利用这些信息将能够更好地对边之间的差异性进行判别,进而提升结构相似性分析过程的剪枝效率。本文将这种节点对结构定义为连接图的结构单元。

根据上述定义,可将装配体模型对应的连接图G分解为结构单元的集合:
S={si,j|h(vi,vj)=1}
(3)
从图论的角度分析,本文定义的结构单元分割方法具有以下特性:
1) 唯一性:对于给定的连接图G,能够将其唯一地分解为若干个结构单元的无序集合。
2) 完整性:能够覆盖连接图G中所有顶点、边、顶点属性和边属性等信息。
如图2所示,2个装配体模型间存在相似结构c,由于结构单元分割的唯一性和完整性,装配体模型对应的结构单元集合Sa和Sb中存在相似的子集Sa,b,即结构c中所包含的结构单元。可以发现,连接图中结构单元所代表的模型信息作为一种局部信息,隐含了其上层装配体模型间的关联线索,这种关联规律在工程领域模型相似性分析中具有较好的适用性。因此,本文中通过结构离散化形成的结构单元,能够支撑装配体模型相似性的分析。

图2 相似结构单元与相似结构的关联Fig.2 Association between similar structural cells and structure
1.3 装配体描述符构建
通过上述结构离散化方法,本文将装配体模型分割为若干个结构单元的集合,进而将装配体模型相似性分析问题转化为以结构单元为基础的分析过程,因此装配体描述符构建过程需要以结构单元的量化描述为基础进行。
1) 结构单元量化描述
形状信息的量化描述是分析三维模型相似性的重要方法,目前在三维模型检索领域已经有较为广泛的应用。较为经典的算法如Osada等[17]提出的形状分布直方图,通过在模型表面上的随机采样计算采样点间距离函数的值,并将函数值的概率分布表示为直方图以描述模型的形状特征,由于具有计算简单、鲁棒性高、识别率较高等特点,这种方法逐渐成为三维模型检索领域较为通用的方法。
本文中的结构单元由于同时具有装配体两零件间的连接信息和零件点云等形状信息,而已有研究中关于连接信息的表达和计算通常较为复杂。因此,本文在形状分布算法的基础上,提出利用结构-形状距离函数将结构单元所包含的结构和形状信息统一纳入一个向量形式的描述符。如图3所示,结构-形状距离可表示为
d=sd+pd1+pd2
(4)
式中:sd为结构单元的空间连接距离,表示两零件重心gc1、gc2到配合面形心fc的距离之和,gc1、gc2和fc由s的顶点和边属性计算得到;pd1、pd2分别为两零件上采样点到该零件形心的距离。
在结构-形状距离函数的基础上,利用文献[17]中形状分布函数的基本思想,通过对模型表面进行随机点采样,并统计距离在尺度范围内的分布情况实现结构单元的量化描述,其具体步骤如下:
步骤1输入结构单元s。
步骤3重复上述步骤,并记录采样结果,通常采样次数不低于105次。
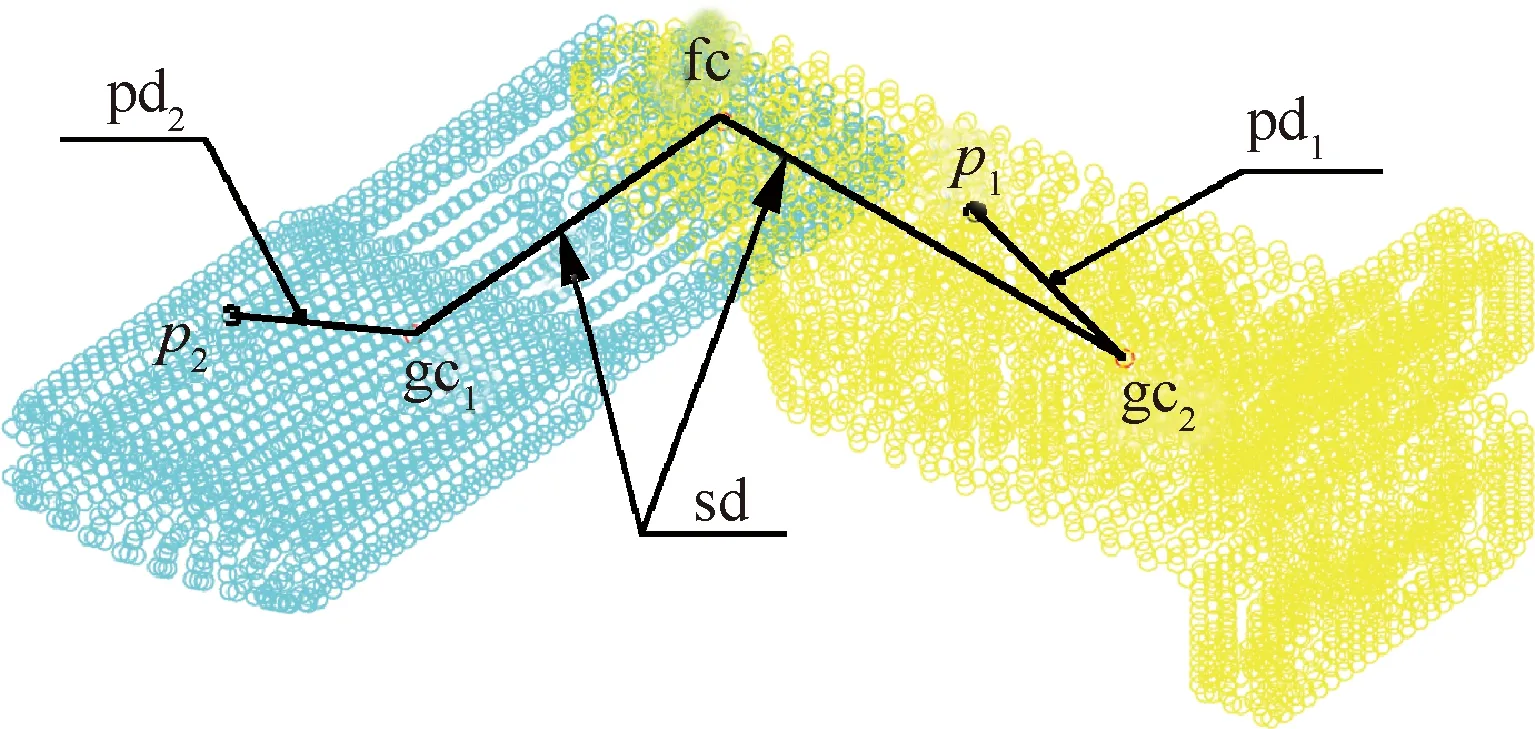
图3 结构-形状距离Fig.3 Structure-shape distance
步骤4构建结构-形状分布直方图。以一个组数为k的直方图表示采样距离值的分布情况,其组距为max(d)/k。根据文献[14],k的取值一般为1 024。直方图中每组的高度表示了每次采样计算的结构-形状距离落在该组中的概率,可以表示为
(5)
式中:ni为第i个组的频数。
步骤5本文不直接使用直方图表示结构单元的结构-形状信息,而是构造一个k维特征向量u=[h1,h2,…,hk]对其进行表征。
步骤6结束。
通过上述步骤能够得到同时反映结构单元形状和空间连接信息的向量描述符。如表1所示,具有相对运动能力的结构单元a与b相比在零件形状上具有一定的差异,相应的结构-形状分布直方图体现为信号形状的差异性;a与c的直方图十分接近体现了本文的描述符对于零件间静态连接和运动连接的适用性;而a与d相比,构成结构单元的两个零件形状上完全相同但装配状态不同,其相应的结构-形状分布直方图在波峰信号起始位置存在差异性。由此可以看出,通过上述步骤形成的结构-形状分布直方图能区分不同形状和连接关系的结构单元,因此能够在一定程度上保证特征向量对结构单元量化描述的准确性。
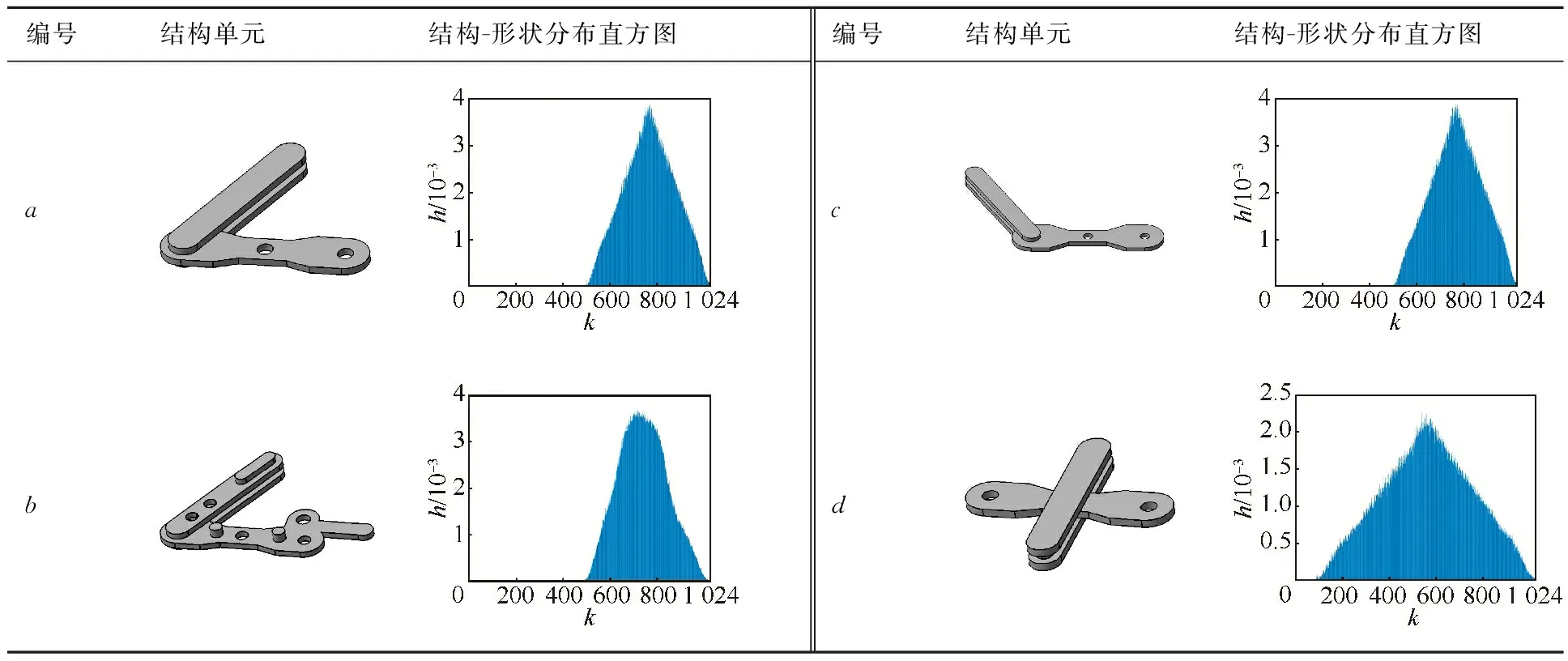
表1 不同结构单元所对应的结构-形状直方图Table 1 Structure-shape histograms corresponding to different structural elements
2) 基于高维向量的装配体描述符
1.2节中,任意的结构单元都可由k维特征向量进行表示,因此本文考虑建立k维特征空间Rk,进而将结构单元映射为空间中的点。对于装配体模型,可根据其中所包含的结构单元,最终由特征空间中相应的k维向量进行表征,其描述过程如下:
对于待描述装配体A,首先构建相应的连接图Ga;然后,根据定义1,按照Ga中节点间的连接关系进行分割,形成结构单元集合{sa,1,sa,2,…,sa,n};最后,对于每一个结构单元sa,i,按照1.2节的结构-形状分布函数将其量化描述为特征向量ua,i,进而得到装配体A的描述符DESa={ua,1,ua,2,…,ua,n}。
通过上述的处理和分析过程可以看出,具有不同形状及连接关系的结构单元能够由特征空间中不同位置的点进行区分,因此不同的装配体模型间的差异性能够通过特征空间中两个点集进行量化分析。
2 装配体模型相似性分析方法
2.1 结构单元相似性度量
结构单元的相似性分析是进行装配体相似性分析的基础。通过上述的步骤,本文最终将结构单元的零件形状及零件间的空间连接关系等信息统一量化表征为结构-形状分布向量,因此结构单元的相似性可通过满足欧氏空间测度公理的距离定义方法进行计算。本文采用L1范式距离(即曼哈顿距离)进行结构单元特征向量的相似性度量。
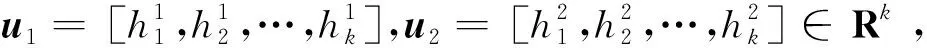
(6)
L1范式距离只与向量中相同维度下的振幅有关,由于每个特征向量中各元素之和为1,L1(u1,u2)取值范围为[0,2]。在此基础上,可将u1,u2所对应的两个结构单元间的相似性归一化表示为
(7)
当dis(u1,u2)=1时,表示两个结构单元完全相同;反之则dis(u1,u2)越趋近于0。
2.2 基于BOW的模型匹配
通过结构离散量化描述过程,本文将装配体检索问题转化为对相似结构单元的搜索问题,因此在检索过程中我们主要关注模型库中与查询模型具有相似性的结构单元。本文在结构单元量化描述的基础上,引入BOW索引与过滤机制,快速过滤与查询模型明显不相关的结构单元,进而提高装配体模型检索效率。
1) BOW倒排索引构造
BOW倒排索引算法是由Csurka等[18]在2004年提出并应用于图像处理领域,其主要借鉴了文档检索的思想。在检索文档的过程中,文档由一系列的基本单元组成,这个单元通常是单词。在本文中,可将装配体模型视为“文档”,其中结构单元所对应的特征向量作为“文档”中的“单词”,进而构建基于BOW的倒排索引结构。主要步骤如下:
步骤1训练码书。对于特征向量数据集,利用K-means算法将特征空间划分为K个子空间,以每个子空间中心点为视觉单词,形成码书C={c1,c2,…,cK}。
步骤2根据码书C将模型库中所有特征向量u量化至最近的视觉单词:
(8)
式中:vi为码书中第i个单词ci对应的高维向量。
步骤3建立倒排索引结构。以视觉单词为索引,将特征向量插入对应的索引列表,形成倒排索引结构,每个索引列表中存储与该视觉单词近邻的所有特征向量,以及包含该特征的装配体。
在索引结构的基础上,通过将查询装配体模型的特征向量量化至对应的视觉单词,能够快速缩小查询范围。
2) 查询过滤
对于查询装配体模型Q的描述符DESq={uq,1,uq,2,…uq,n},n为特征向量数量,其搜索过程可以被近似地视为在倒排索引结构上进行n次近似最近邻查询。
为了提高查询结果的召回率,本文采用超球体软分配策略,通过查询点与视觉单词分布半径间的距离关系自适应地为查询样本分配若干个匹配视觉单词,计算过程见文献[19]。对于每个查询特征向量uq,i,将为其分配的视觉单词内所有特征向量作为匹配候选集:
mi={list(cj)|Bi(c1≤j≤K)=1}
(9)
式中:B为指示函数,Bi(u1≤j≤K)=1为与查询向量uq,i匹配的视觉单词;list(cj)为第j个索引列表中所包含的所有特征向量。对于查询装配体模型Q,可将匹配结果表示为
M={m1,m2,…,mn}
(10)
对于模型库中任意装配体A的描述符DESa={ua,1,ua,2,…,ua,m},m为特征向量数量,DESq中每个特征向量与DESa的匹配关系可表示为
Ma={ma,1,ma,2,…,ma,n},ma,i=mi∩DESa
(11)
式中:ma,i为装配体A中与uq,i匹配的特征向量集合。与原始搜索空间相比,集合Ma过滤了特征空间中距离DESq的较远的特征向量,进而避免对数据库的线性扫描。Ma中匹配特征向量的数量能够在一定程度上反映装配体模型间的相似性。
基于BOW算法通常能够使查询复杂度达到logN级别,因此在上述计算过程中,当以一个装配体模型为查询对象时进行匹配时,其复杂度为O(NMlog(KNM)),其中N,M分别为所有装配体模型中零件的平均数量以及每个零件连接关系的平均数量;K为模型库的规模。在最差情况下,即模型中任意两个零件间都存在连接关系,此时匹配过程的时间复杂度为O(N2log(KN))。而以Ullmann等子图同构算法对模型库进行匹配时,其最差情况下时间复杂度为O(KN!N2)[20]。由此可见,与已有基于图匹配的方法相比,本文所提出的模型匹配方法在计算复杂度方面有了较大的提升。
2.3 装配体相似性量化分析
装配体模型作为若干个结构单元的集合,模型间的相似性是由相应集合中元素间的最优匹配所决定的。即建立两个装配体中结构单元的一一对应关系,使得该对应关系下结构单元的相似性总和最大。考虑到Ma中特征向量间存在一对多或多对一等匹配形式,本文利用Earth Mover Distance算法[21]求解两集合间的最优匹配,进而对装配体模型的相似性进行进一步量化分析。

(12)
(13)
3 实验分析
为了验证本文方法的有效性,在CATIA V5R19环境中通过二次开发实现零件几何信息提取的批量化处理,并在MATLAB R2019b平台下实现零件连接分析、结构-形状分布函数、索引过滤和装配体相似性度量等,实现了本文所提出的基于结构离散化的装配体模型检索方法。实验数据库包含260个装配体模型,共计1 984个零件模型,模型库中部分装配体模型如图4所示。
3.1 检索实例
本文在模型库中选取脚轮和夹钳两组模型进行检索实例分析,两组中模型数量分别为24和15个,实验中分别在其中选择一个装配体模型作为输入,并对返回结果的相似性进行排序形成检索结果,如图5所示。

图5 装配体模型检索实例(K=128)Fig.5 Retrieval instances of assembly model (K=128)
从相似度角度分析,2组实验中第一个结果相似度均为1,是因为该检索结果是查询模型本身。(a)组实验中前4个与后4个和(b)组实验中前5个与第6个结果的值差异较大,说明相似性度量值受匹配结构单元数量影响较大。对于越相似的装配体模型,其中存在的匹配结构单元数量也随之增多,因而相似度值越大。但从总体来看,排序越靠前的检索结果与查询模型的相关度越高,证明本文提出的装配体相似性测度方法具有一定的合理性。由于装配体描述符在构建过程中考虑了零件间的连接关系信息,在装配体连接关系不变的情况下,对不同姿态下的模型可以得到一致的描述结果。例如在(b)组实验中,对于结构较为相似但处于不同姿态下的装配体模型,计算后的排序位置为第2和第3位,可认为与查询模型的相似程度较高。由此可以看出,本文提出的描述方法对于具有相对运动的装配体模型也具有一定的识别能力。
在返回结果中,模型中灰色部分零件表示其所在的结构单元在索引结构中被过滤。从(a)组实验5~8个结果与查询模型进行对比发现,黄色部分模型与查询模型间的相似性较高,说明本文的算法能够较好地过滤与查询模型无关的结构单元,因而在一定程度上具有识别模型局部结构相似性的能力。
从准确性角度分析,(a)组实验检索效果较好,而(b)组实验中第7个结果出现错误,一方面是因为后者与前者相比模型数量相对较少,导致出现错误概率更高;另一方面是由于本文中结构单元的特征向量是利用结构-形状函数通过多次采样形成的概率分布,这种方法不可避免地存在“语义鸿沟”问题,进而导致错误结果的产生。图6为以不同数量结构单元为查询对象下返回的前6个检索结果。当以独立的结构单元进行查询时,第4和第6位结果出现明显错误;但(b)组结果在准确率上有了一定的提高,是因为本文的相似性测度过程与结构单元匹配数量密切相关。当输入的查询结构单元数量越多时,模型库中具有相似结构的正样本模型与其他负样本模型相比,前者存在更多的匹配结构单元,因此具有更高的“概率”获得更高的相似性度量值,进而能够保证检索结果的合理性。
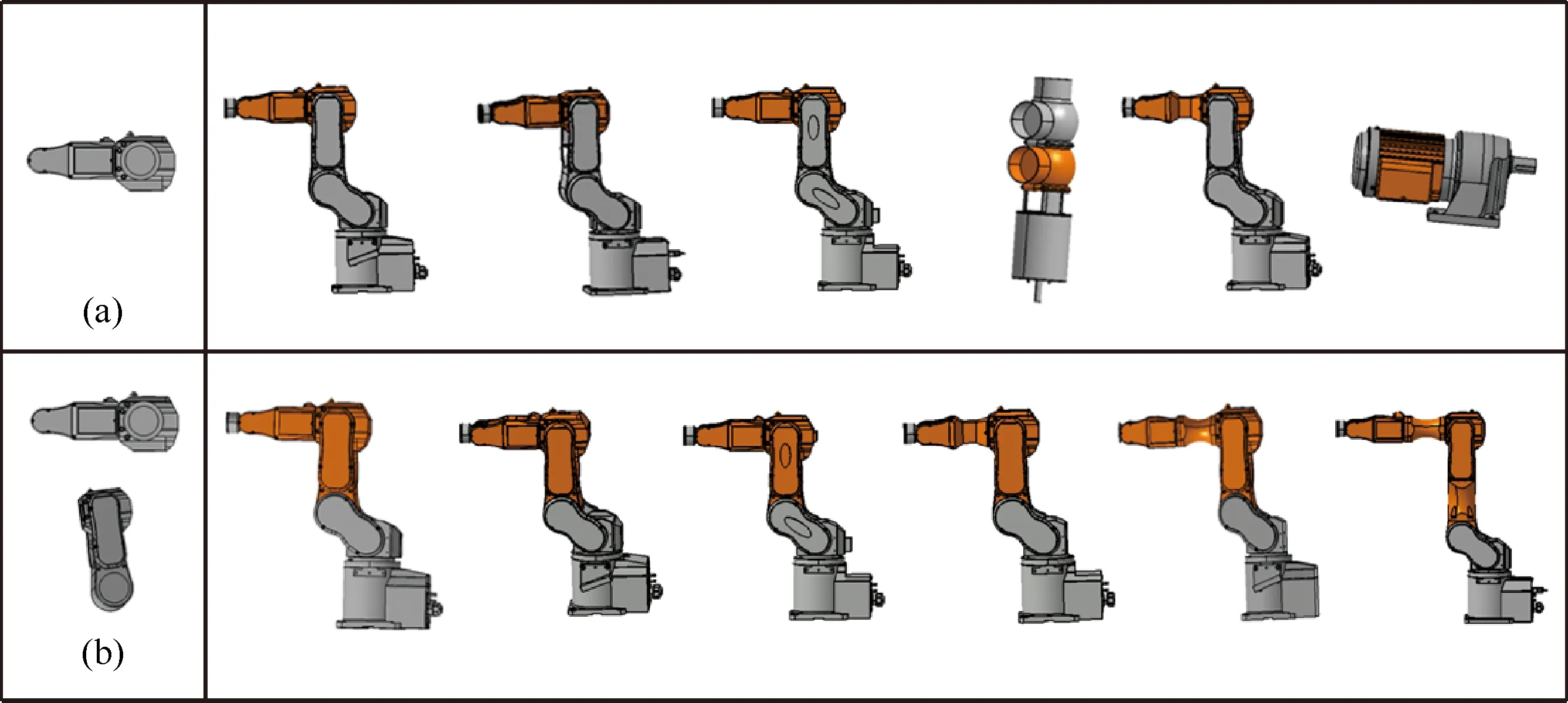
图6 输入不同数量结构单元的返回结果Fig.6 Results for inputting different number of structural cells
3.2 检索性能
在信息检索领域,通常将查全率(Recall)与查准率(Precision)作为反映检索性能的重要指标。其中,查全率反映原有样本中有多少正例被准确预测;查准率表示预测为正的样本中有多少是真正的正样本(True positives)。图7给出了本文方法在查询结构单元数量n=1,2和以整个装配体为查询对象下的查全率-查准率(P-R)曲线。
n=1,2时,其查全率未能达到1是因为存在实际为真的实验样本在索引结构中被过滤,因此被错误地预测为假。从总体来看,虽然n=1时在查全率较高情况下检索结果准确率较低,但随着查询结构单元数量逐渐增多,相同查全率水平下所得的查准率都相对有所提升,与图6所得基本结论一致。由此可见,本文算法在检索性能上具有一定的柔性:当对查询查准率要求较高时,如在模型库中查找包含一个常用部件的所有装配体模型,以部件中包含的所有结构单元作为查询对象能够返回更准确的结果;而在查询部分关键结构的演化版本时不需要很高的查准率,因此可以以部分结构单元为查询对象以获得更多参考。

图7 查全率-查准率曲线(K=128)Fig.7 Precision-recall curves (K=128)
3.3 视觉单词数量K对检索的影响
在2.2节建立索引结构过程中,引入变量K用于构建视觉单词和索引字典。图8为过滤效率、召回率与视觉单词数量K之间的关系,实验中所用K的数量分别为16,32,64,128,180,256。由于索引和过滤计算过程中是以独立的特征向量为查询对象多次进行的,因此本节只统计n=1的情况下检索结果的过滤效率和召回率指标。
从图8中可以看出,随着K的不断增加,过滤效率与召回率增长趋势相反:K在16~128之间时,过滤效率迅速提升,召回率始终在95%以上;K超过128时,过滤效率维持在较高水平而召回率迅速降低。其原因是随着参数K的不断增加,特征空间的划分也更加精细,导致同一类结构单元更有可能被划分至不同的子空间,进而导致召回率的降低。因此,本文在实验中K取值为128,能够在过滤效率和召回率间取得较好的平衡。
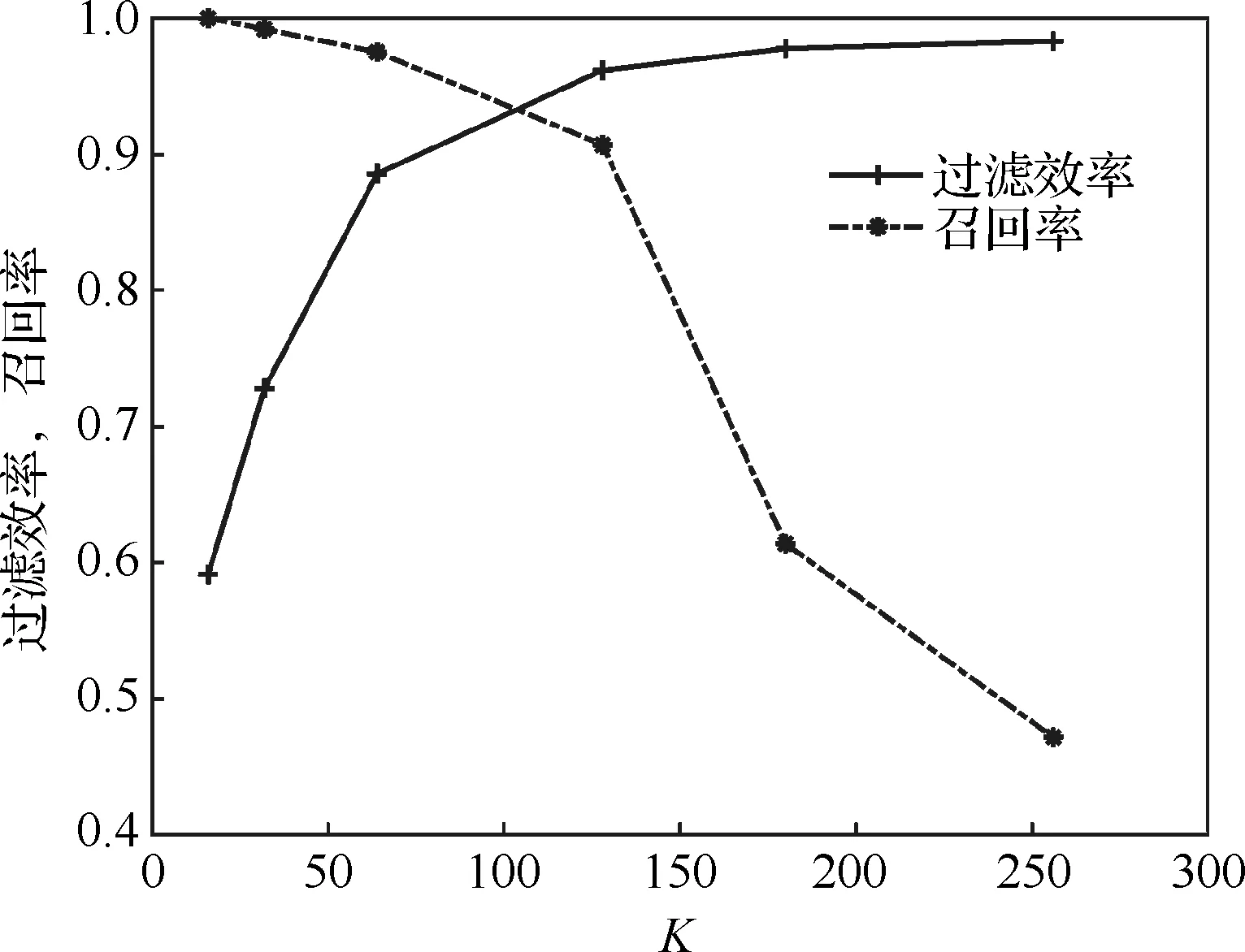
图8 过滤效率、召回率与K的关系Fig.8 Relation of filtration ratio, recall ratio and K
4 结 论
1) 提出了基于结构离散化的装配体模型信息量化方法,通过模型结构单元的分割和形状-结构距离分布的统计等过程,实现装配体模型结构特征的向量化描述。
2) 探讨了基于BOW算法的倒排索引结构和超球体软分配算法在装配体模型检索领域的应用,能够在查询过程中快速过滤无关的对象。
3) 建立了基于EMD算法的模型相似性度量方法,通过相似性度量值的排序获得查询结果,实例验证了本文方法的有效性。
