精密复杂曲面零件多轴数控加工技术研究进展
2021-12-02徐金亭牛金波陈满森孙玉文
徐金亭,牛金波,陈满森,孙玉文,*
1. 大连理工大学 汽车工程学院,大连 116024 2. 大连理工大学 机械工程学院,大连 116024
多轴数控加工是现代工业中的标志性加工技术,在能源、动力、国防、运载工具、航空航天等高端制造领域的关键零部件加工中占据着主导地位。随着中国在这些制造领域的不断拓展,涌现出一大批加工难度大、性能指标要求苛刻的精密复杂曲面零件,如大型航空运载工具的精密壳体、天线罩、航空发动机的机匣及叶片、整体叶轮和叶盘等,因其超常规的使役环境,常以导流、透波、抗疲劳特性以及气动特性等性能指标为主要制造要求。为满足性能指标要求,此类零件的形状及结构日趋复杂,通常具有薄壁悬垂、极端大尺度比等特点,而且壁厚变化剧烈并且有着严格的控制要求,加工精度不断提高,其制造已由以往单纯的形位精度加工,跃升为形位与性能指标并重的高性能加工,给目前的复杂曲面数控加工技术带来了严峻的挑战[1-2]。
数控加工是由模型曲面上的加工路径直接驱动,因而高效加工路径设计方法成为提高加工效率,保证零件表面成形精度的关键[3]。然而,传统路径规划方法却拘泥于单纯几何学层面的逐点路径设计和离散调整,从运动学及切削特性层面考虑加工路径拓扑几何形状的方法较少,无法兼顾曲面几何物理特性、难以实现路径的整体调控。在复杂曲面的数控加工中,运动规划也非常重要,特别是在复杂零件的高速高精度加工中,适应性进给率定制技术是加工精度和加工效率保证的有效手段[4]。目前,进给率定制局限于在前瞻预读框架下构建不同形式的弧长-时间及进给率-弧长映射的常规方法,尚未完全建立起轨迹内在几何特性与进给率运动特性间的联系,其定制过程通常需要多次反复,以求在多种约束许可范围内获得尽可能高的速度,并在提高加工效率的前提下保证加工精度。数控加工既是一个零件的几何成形过程,也是一个复杂的动态物理切削过程,特别是随着高档数控机床切削速度不断提高,对数控加工技术的研究不能仅关注常规几何学层面的走刀路径设计和运动学层面的运动规划,必须转向实际的物理加工过程,解决大进给量、高转速所带来的刀具负载波动、变形、破损失效,特别是解决加工过程中由于切削力变化所引起的切削系统的不稳定等问题。
实际加工中,单一层面的工艺规划、依赖经验的工艺参数设置,极易导致加工过程失稳、几何误差失控、加工表面完整性破坏,严重影响零件的使役性能,甚至导致零件报废。高性能精密复杂曲面零件的数控加工不仅对加工路径的拓扑几何形状、运动学性能提出了更高的要求,对加工参数的选择以及动态切削过程的控制也极为严格。然而,当前与复杂曲面数控加工密切相关的CAM (Computer-Aided Manufacturing)系统如NX、Mastercam等却大都只从几何学层面考虑加工路径设计,尽量避免局部加工干涉和全局碰撞,忽视了加工路径运动学特性及切削过程动态特性对精密复杂曲面零件成形精度以及加工表面微观形貌对零件使役性能的影响[5];而依据机床刀具制造商所提供的通用数据库,或凭常规切削经验所设定的加工参数如主轴转速、进给速度及轴向和径向切削深度等又相对保守,难以对影响零件使役性能的表面质量进行控制,致使高档数控机床的许多优良加工特性难以发挥,这不但造成制造企业的高速加工设备依旧在常规工况下运行,也严重限制了精密复杂曲面零件成形精度和加工效率的提高及对表面质量的精确调控。可以说,精密复杂曲面零件的高性能数控加工是以工艺系统动力学为基础,以形位精度保证、加工效率提升及动态切削过程可控为核心,体现在加工路径设计、进给率定制、切削过程动力学分析和切削参数优化配置等各个环节。本文将围绕上述各个环节,详细论述相关加工技术的研究现状、存在的难点和核心问题,指出可行的解决途径、突破方向和未来的发展趋势,为复杂曲面的高性能数控加工提供参考和依据。
1 多轴数控加工路径设计
高效的加工路径设计方法一直是数控加工领域中的研究热点。围绕优化加工路径,充分发挥高档数控机床加工潜能、提高零件加工效率及成形精度这一目标,研究人员已经从不同的角度和侧面针对多轴数控加工路径设计展开了一系列的研究[6-7]。因此,本节将从刀具轨迹规划、刀具姿态调整、加工奇异性避免以及加工路径光顺等方面进行详细论述。
1.1 多轴数控加工的刀具轨迹规划
刀具轨迹的实质是在最大加工残留高度约束下能够通过合理排布实现对整张曲面有效覆盖的一族曲线。因此,可以将刀具轨迹规划分为曲面上曲线族的选择和有效排布方式的合理设计2个方面[8]。曲面上的曲线可以是等参数线、等截面线、等残留高度线以及测地线等,轨迹排布方式又可分为Zig-zag排布、环形排布、螺旋排布等。在实际轨迹规划中,可根据计算的复杂程度、加工方式、精度及效率等方面的要求,选择不同的曲线族及排布方式,生成符合实际生产条件和加工要求的刀具轨迹。常用的刀具轨迹有计算简单的等参数刀具轨迹[9-11],注重加工效率的等残留高度刀具轨迹[12-15]以及适用参数曲面、点云和网格等多种描述模型的等平面刀具轨迹[16-18]等。
为增强这些传统方法的适用性、提高实际加工效率,研究人员利用裁剪曲面的重新参数化发展出了能够保持裁剪边界一致性的等参数轨迹规划方法[19-21]及螺旋轨迹设计方法[8,22];通过合理地选择初始驱动轨迹替代边界曲线,进一步缩短等残留刀具轨迹的长度[23-24];考虑曲面整体曲率分布、切削方法及表面粗糙度要求,优化平行截面与曲面的截交方向以提高加工效率[25]。作者团队将曲面协调映射的基本原理引入到数控加工领域,以降维规划的思想(如图1所示)实现了刀具轨迹几何计算复杂性的精简,以网格曲面为统一架构的基础,解决了不同类型曲面上光滑连续高性能刀具轨迹规划问题,先后提出了网格曲面上的等参数刀具轨迹设计方法[26]、拼接裁剪曲面的边界一致性加工方法[27]、零亏格及非零亏格曲面上的高速螺旋刀具轨迹设计方法[28-32],提出了空间开/闭变距刀轨复杂局部/全局自交干涉的统一消除准则[33]、网格曲面上的变距刀轨设计方法[34]以及含有空洞的复杂曲面环切路径生成方法[35-37]等。上述刀具轨迹规划方法计算简单鲁棒,在数控加工中占据着主导地位,严格来讲这些研究仍属于常规加工的静态几何学范畴,只关注沿刀具轨迹加工的几何可行性,并未考虑机床加工能力、刀具切削方向、加工过程动态切削特性对复杂曲面零件成形精度、加工效率以及零件表面物理性能的影响。
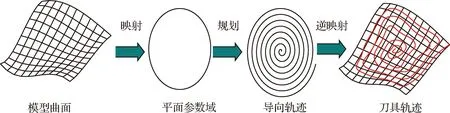
图1 基于曲面协调映射的刀具轨迹规划的基本思路Fig.1 Basic idea for planning tool path based on harmonic mapping
在刀具轨迹规划中引入走刀矢量场的概念,综合考虑曲面几何特性及其物理性能、刀具运动及切削过程动态特性已经成为该领域的研究热点和未来发展趋势[38-40]。为了能够融合数控加工中的几何及物理信息,模型曲面首先被均匀采样,在每一采样点处确定最优走刀方向,如最大切削带宽方向[38, 41-44]、进给速度最快方向[45]、材料去除率最大方向[46-47]、运动学性能最佳方向[39]、切削力及变形最小方向[47-49]、表面流线方向[50]、能耗最小方向[51],甚至可在每一采样点处指定能够反映设计意图的最优走刀方向。这样,所有采样点处的最优走刀方向构成了能够实现数控加工几何物理信息统一描述的最优走刀矢量场(图2[43]为参数域上的切削带宽最大矢量场),如何在场的统一描述下,构造能够严格遵循曲面各点处最优走刀方向的刀具轨迹就成为必须解决的关键问题。

图2 参数域上最大切削带宽走刀矢量场[43]Fig.2 Vector field for maximum cutting width in parametric domain[43]
Moodleah[47]、Manav[49]等利用启发式搜索算法沿最优走刀方向遍历各个节点,构造能够尽量遵循各点最优走刀方向的刀具轨迹。但离散节点的遍历搜索及点线连接,将不可避免造成频繁的轨迹转接及走刀中断,点线连接路径在邻接面片间也很难实现光滑过渡。Chiou和Lee[38]提出,首先根据整体走刀方向构造一条沿最优走刀方向的主轨迹,然后利用曲线偏置策略实现最优走刀方向刀具轨迹在曲面上的整体排布。在此基础上,Kumazawa[43]、Liu[44]等利用走刀矢量场的退化点对曲面进行区域分割,然后在各个区域上再选择一条主轨迹,利用曲线偏置生成刀具轨迹。但受限于传统的曲线偏置操作,主轨迹一旦选定,整体轨迹的排布形式及走刀方向就会受到严格限制,尽管沿主路径对最优走刀方向的偏离最小,但由于曲面各点处走刀方向的各向异性,相邻轨迹上的走刀方向会逐渐偏离最优走刀方向。为解决这一问题,作者团队引入流线场的概念[40],将参数域上最优走刀矢量场看作是平面无旋流动的流线场,通过重构能够发生走刀矢量场的流函数及最大残留高度约束下流线场中流线的求解,实现严格遵循各点最优走刀方向的刀具轨迹的计算[52],并进一步证明了拼接曲面间流线场的G1连续光滑耦合拼接条件,实现了复合曲面上刀具轨迹的光滑过渡[53](见图3)。
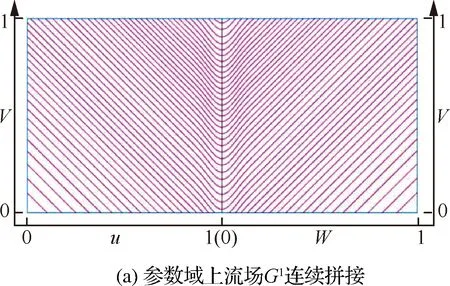
图3 基于流线场光滑耦合拼接的复合曲面上流线型刀具轨迹构造[53]Fig.3 Planning stream-like tool paths on compound surface based on blending multiple vector fields[53]
1.2 五轴数控加工的刀具姿态优化
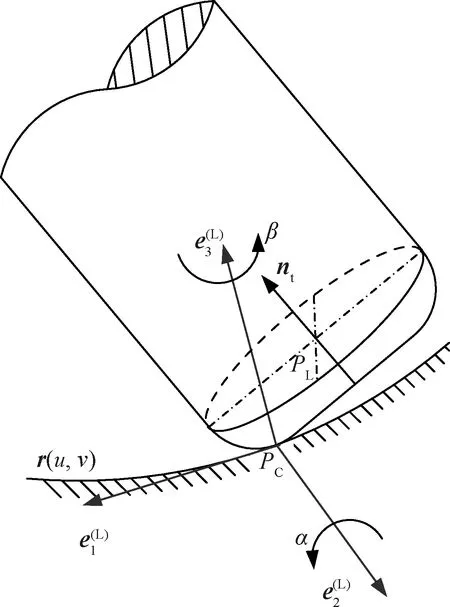
图4 刀具姿态Fig.4 Tool orientation
最初,关于五轴数控加工刀具姿态的研究主要集中在如何避免加工过程中可能出现的刀具局部干涉及全局碰撞上[54-55],先后提出了用于消除局部加工干涉的曲率匹配法[56-57]、多点接触法[58]、弧交法[59]、滚球法[60]和球头刀专用的曲面偏置法[61]等,以及用于判断及消除全局碰撞干涉的构型空间(C-space)法[62]、基于可视锥的碰撞消除法[63]以及基于物理引力场的无干涉刀具姿态确定方法[64]等。同时,Barakchi Fard[41]、Bedi[65]、Chiou[38,66]等尝试在刀触点处调整平底刀或环形刀的姿态以增大加工带宽。在圆柱铣刀侧铣中,Gong[67-68]、Zhu[69-70]等通过调整刀具姿态,实现了刀具曲面与设计曲面间的高阶密切,从而能够有效提高加工精度,增加材料的去除率。这些方法基本上都是刀触点邻域内的局部优化,通过离散刀触点处刀具姿态的局部调整,达到避免加工干涉、增加加工带宽的目的。但仅仅为了避免加工干涉或增大加工带宽的刀具姿态调整,可能会导致相邻刀触点间刀具姿态发生剧烈变化[55]。如果相邻刀具姿态变化过于剧烈,就可能导致实际加工过程中机床各旋转轴的速度、加速度及加加速度超出机床驱动轴性能限制的情形出现,致使加工过程失稳、破坏加工表面的完整性[30]。
实际上,刀具姿态确定不仅要从几何学层面考虑加工精度、避免刀具干涉碰撞,其选取也受到相邻刀触点甚至整条刀具轨迹上刀具姿态变化的限制,必须考虑刀具姿态变化的光顺性以及其变化与机床运动学性能间的关系,因此光顺刀具姿态的研究引起了研究人员的重视。最初研究都是在工件坐标系下光顺刀轴矢量,如Jun等在α-β平面上构造满足残留高度要求及加工干涉约束的可行域,然后通过前向及后向搜索从所有刀触点可行域边界确定2条路径,其中刀轴矢量角度变化总和最小的路径被用于产生光顺的刀轴矢量[71]。Lauwers等提出通过控制单位路径上刀具的摆动角度来产生光顺无碰撞的刀具姿态[72]。Ho等提出基于四元数插值(也称为球面线性插值)的刀轴矢量光顺方法,在满足加工精度的同时尽可能地提高刀具的运动学性能[73]。考虑到相邻刀触点间刀具摆动的角速度限制,Wang和Tang率先提出了刀具摆动角速度及局部加工干涉约束的刀轴矢量光顺方法[74]。Sun等进一步将刀具摆动的角速度、角加速度以及角加加速度限制融入刀轴矢量光顺之中,提出了沿指定进给速度轮廓的双样条刀轴矢量光顺方法[75]。Huang等利用径向基函数对关键刀触点处指定的刀轴矢量进行光顺插值,从而确定其他刀触点处的刀具姿态[76]。需要注意的是,由工件坐标系到机床坐标系逆向运动学变换的非线性,导致工件坐标系下的光顺刀轴矢量无法保证机床各旋转轴运动的平稳光顺,机床旋转轴上的动力学负载依旧可能发生突然剧烈的变化。
最近研究表明,在机床坐标系下以五轴机床旋转轴运动平稳光顺为目标的刀轴矢量光顺方法能够有效改善机床旋转轴的运动学性能,避免旋转轴上的动力学负载产生突变[77-79]。在机床坐标系下优化刀轴矢量已成为目前该领域的研究热点。Castagnetti等[80]在工件坐标系下构建无局部干涉及全局碰撞的简化刀具可行域(Domain of Admissible Orientation,DAO),然后利用逆向运动学变换将其映射到机床坐标系下(如图5所示),以机床坐标系下的DAO为约束,建立以机床旋转轴运动坐标变化最小为目标的优化目标函数,并利用基于梯度的优化方法进行求解,从而实现直接面向旋转轴运动的刀轴矢量优化。同样,在刀具可行空间中,Hu和Tang以机床旋转轴角加速度最小为优化目标,利用基于启发式的遗传算法进行求解,确定各刀触点处的最优刀具姿态[81]。Plakhotnik和Lauwers[82]指出,如果只调整刀具的后跟角,刀具在刀触点处的可行空间可简化为一条圆弧(如图6[82]所示),机床旋转轴坐标变化最小就可简化为利用Dijkstra算法在所有可行弧上搜索最短路径问题,类似工作也可见文献[83-84]。Xu等利用B样条曲线对通过逆向运动学变换得到的离散旋转轴坐标进行拟合,以实现旋转轴运动的光顺[85]。可以看到,机床坐标系中刀具可行空间约束下的刀轴矢量光顺是一个复杂的约束优化问题,上述方法大都采用启发式算法或基于梯度的优化方法进行求解。但由于每一刀触点处刀具可行空间形状各异,导致干涉约束条件很难被解析表示,这极大地增加了刀轴优化问题求解难度[80]。为了解决这一问题,作者团队提出了刀轴光顺与干涉检查轮换迭代的优化策略,首先指定关键刀触点处的刀具姿态,然后以旋转轴角加速度最小为目标,通过最小二乘方法插值其余刀触点处的刀具姿态,然后判断所插值的刀具姿态是否在刀具可行空间之中;将不在可行空间中的刀具姿态重新指定,再次进行插值与检查的轮换迭代,直至所插值的刀具姿态都在刀具可行空间之中[30, 86]。
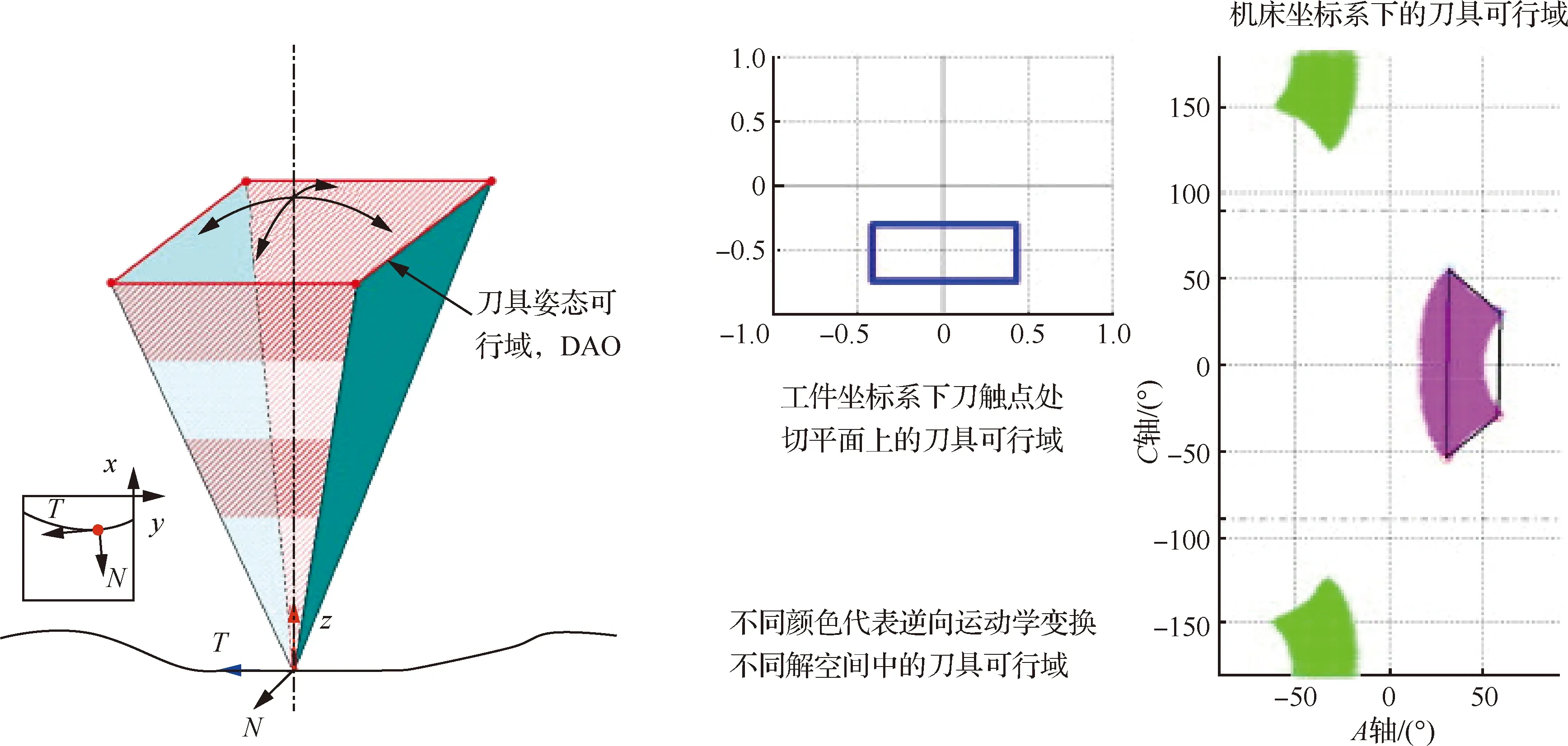
图5 工件坐标系及机床坐标系下简化的刀具可行域[80]Fig.5 Domain of admissible orientation in workpiece coordinate system and machine coordinate system[80]
上述面向运动学性能的刀具姿态优化方法能保证加工过程中机床旋转轴运动的平稳光顺,改进零件表面加工质量,但应注意到零件的最终成形质量还决定于加工过程中的切削力、变形、振动等动态切削特性。基于这一考虑,目前刀具姿态优化的研究正逐渐从保证刀具运动几何可行的干涉碰撞消除、机床驱动轴的运动平稳光顺,向在加工过程几何与运动学约束下的切削特性改善方向发展[87-88]。例如,考虑到刀具姿态变化会改变刀具与工件的接触区域,从而影响到切削速度、未变形切屑厚度等,导致切削力改变、产生变形及振动,Layegh等[89]讨论了刀具姿态变化对切削力波形、扭矩以及工件变形的影响,给出了基于切削机理的刀具姿态确定图谱,帮助选择刀具姿态,改善加工质量。Sun和Altintas[90]进一步讨论了刀具姿态变化对铣削颤振的影响,给出无颤振刀具姿态确定方法,实际加工实验表明所提方法能够显著减少振纹,提高加工表面质量。同样地,在无颤振等加工过程动力学特性约束下,Huang等[91]给出了基于最大最小优化准则的刀具姿态确定方法。最近,Wang等[92]提出了维持切削性能的刀具姿态优化方法(Cutting Performance Maintained,CPM),能够在干涉碰撞几何约束及机床驱动性能约束下,通过局部刀具姿态的微调,在尽可能维持初始刀具姿态切削性能不变的条件下显著提高五轴加工过程的运动学特性。
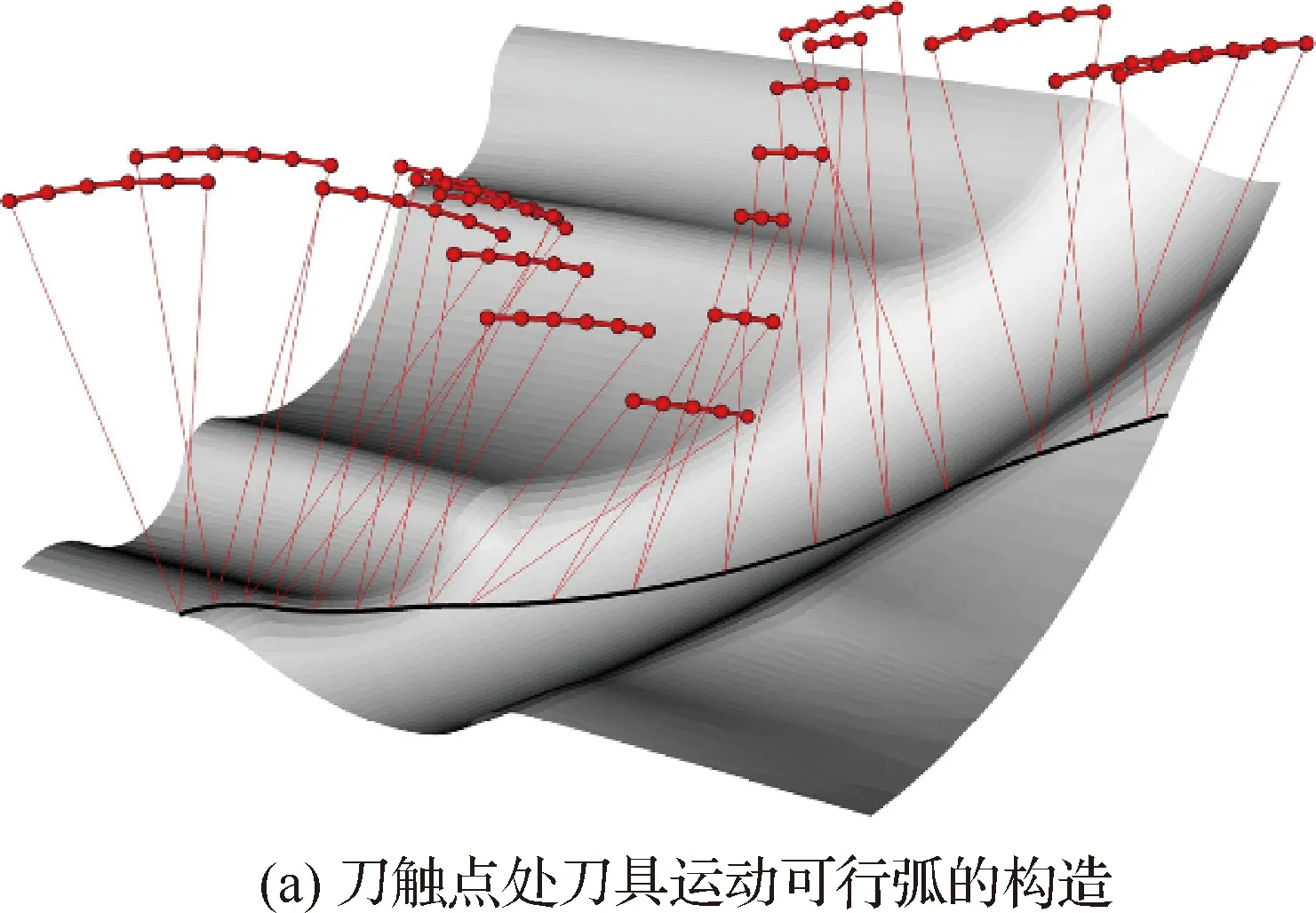
图6 基于刀具运动可行弧和机床坐标系下Dijkstra算法的最优刀具姿态确定方法[82]Fig.6 Method for optimal tool orientation based on admissible arc and Dijkstra algorithm in machine coordinate system[82]
1.3 五轴数控加工奇异性避免
五轴数控加工的奇异性避免属于刀具姿态优化的范畴,但其关注的重点是机床奇异点附近刀具姿态的优化调整,直接影响工件表面质量,是加工路径设计中必须避免的关键问题,因此本文将其单独列出论述。在理论上,机床奇异点对应于刀具轴线与机床第二旋转轴平行位置。Cripps等[93]证明,当刀具经过或接近该位置时,机床除第一旋转轴外的其他运动轴的速度会产生不连续且急剧转动,引起机床旋转轴运动失调、加工精度降低及表面质量退化,甚至导致撞刀、损害机床驱动部件。最初,奇异运动被认为与逆向运动学变换求解有关,Munlin等[94]通过优选奇异点附近的旋转轴角度组合以减小角度变化过大带来的运动误差。Sørby[95]认为密化奇异位置附近的刀位数据有利于旋转运动的连续性,并提出了相应的后置处理算法。Boz和Lazoglu[96]通过后置处理,修改奇异点附近的旋转角度以减小运动突变。但上述方法并未考虑机床驱动轴的运动学特性,由于机床驱动轴运动学超差导致的加工失稳仍难以消除。
实际上,五轴机床的运动结构决定了加工奇异性难以从根源消除。为避免五轴加工中的奇异问题,应确保刀具运动尽可能地远离奇异点。考虑到工件坐标系与机床坐标系之间的非线性关联,工件坐标系中确定的刀具路径在不同装夹方式下会呈现不同的运动形式,进而影响机床的切削性能。Pessoles[97]和Cripps[93]等先后对工件装夹与奇异运动之间的关系进行了研究,表明更改工件的装夹方向可以在保持原有路径不变的情况下实现免奇异加工。但该类方法并不能保证可行解的存在性,并可能导致干涉碰撞、行程超差等问题。为保证奇异避免的可靠性,在路径生成阶段,通过调整路径以避免奇异是目前最为常用的奇异避免方法。Lin等[98]提出,在C平面上使用最短的平移向量整体平移刀轴投影曲线远离奇异域,以实现免奇异加工,并通过优化平移向量,在奇异避免的同时,保证了零件曲面的加工纹理[99]。考虑到既定刀轴的全局调整会改变刀具的切削特性,带来额外的加工问题,通过加工路径的局部调整来避免加工奇异性问题就成为首选。据此,Affouard等[100]使用旋转轴的定位精度定义了“奇异锥”,在将五轴路径表达为双B样条形式的基础上,通过局部调整样条控制顶点以使刀轴脱离“奇异锥”实现了奇异的避免。类似,Yang和Altintas[101]通过旋转与奇异路径相关的控制点,使其远离奇异域。Wan等[102]提出了一种奇异域限制下的路径调整策略,进一步限制了Yang和Altintas提出的调整区域。
注意到,上述方法只在工件坐标系中讨论了五轴加工奇异性的避免,并没有考虑刀轴调整后机床的运动学特性。正如之前所讨论,直接面向机床运动特性的刀具姿态调整对保持机床运动学性能和刀具切削特性更为有益。文献[80, 103]研究了机床坐标系下,考虑运动学特性的奇异避免方法。然而,对于五轴非球头刀加工,刀轴的变化会带来刀具与工件接触特性的改变,引发过切干涉等几何问题与切削力变化等物理问题,因此在奇异避免的同时,既能保证加工无过切,又能兼顾机床运动性能,对提高五轴数控加工性能更具实际意义。为此,Sun等[87]通过将奇异避免,过切约束及机床驱动轴运动学特性约束转换为边界与线性条件,构造了以旋转轴角加速度之和最小为目标的二次优化模型,通过该模型可得到无过切干涉且运动特性良好的无奇异性刀具姿态。
1.4 数控加工路径光顺优化
常用的线性加工路径(即G01代码)在拐角处的切向及曲率不连续容易造成机床各驱动轴频繁地加减速,从而影响工件的加工效率和质量。为了提高加工运动平稳性及高效性,需要在轨迹插补指令生成前,对拐角处的线性路径进行光顺,这也是当前数控加工领域中的研究热点[104-109]。为了实现刀具轨迹的光顺,参数样条被广泛用于构造拐角过渡曲线。目前采用的样条曲线主要有NURBS曲线[110-111]、B样条曲线[112-114]、Bézier样条曲线[115-117]以及PH曲线[118-120]等。在转接路径的连续性研究中,Zhang等[121]首先采用三次Hermite样条曲线完成了对空间连续小线段路径的光顺优化,推导了满足C1连续性条件的样条控制点参数,但未考虑路径转接处加速度连续对构建样条的约束。为此,Zhao等[122]引入带有5个控制点的三次B样条曲线,给出了满足误差约束的过渡曲线曲率极大值的快速解析求解模型,并融合前瞻S曲线加减速规划实现了G2连续的刀具路径在线平滑光顺。随后,Fan[115]、Zhang[123]等分别利用四次Bézier曲线和五次B样条曲线,先后提出了满足G3连续的微小直线段刀具路径光顺插补算法,证明了G3连续的刀具路径相比G2连续的刀具路径在提高加工效率、减小进给率波动方面拥有更好的调控能力。围绕此类连续性问题,Fan等[124]最近基于九次Bézier曲线,进一步构建了满足G4连续性条件的路径转接规则,并提出了一种加加速度光顺的进给率实时规划方法。
对五轴加工而言,不仅需要考虑刀尖点轨迹的光顺优化,还需对刀具姿态运动进行光顺约束,因而一直备受科研人员的重视。通常,五轴刀具姿态运动在球面坐标系下进行描述,其路径优化相比笛卡儿坐标系下的刀尖点运动路径更加复杂。此外,光顺后的刀尖点运动路径和刀具姿态运动之间的参数同步性要求,也使现有的三轴路径优化方法难以直接应用于五轴路径优化。在早期的研究中,Beudaert等[125]采用2条三次B样条曲线分别对刀尖点运动和刀轴方向进行G2连续的路径光顺,并通过引入另1条三次B样条曲线来实现刀尖点运动路径和刀具姿态运动之间的参数同步。Tulsyan和Altintas[106]利用五次B样条曲线和七次B样条曲线完成了对五轴刀尖点运动路径和刀具姿态运动之间的同步,实现了五轴数控加工路径的光顺优化,该方法能够对刀轴方向转接误差进行直接控制。但由于过渡圆弧长度与样条曲线参数之间存在高度非线性关系,使得在确保具有较高计算效率和优良动态性能的同时,难以开发具有高阶连续性的实时拐角光顺和插补算法。为解决这一问题,Bi等[116]通过2条三次Bézier曲线分别对机床坐标系下的平动轴指令和旋转轴指令进行光顺,推导了刀尖点路径与刀轴方向之间参数同步的解析关系,并通过涡轮加工实例验证了该方法的实时性。随后,Yang和Yuen[107]采用配置B样条曲线控制点的方式,分别在工件坐标系和机床坐标系下对刀尖点运动路径和旋转轴路径进行几何光顺,提出了一种具有C3连续的实时路径光顺算法。考虑到刀轴方向转接误差为非线性角度误差,在机床坐标系下对旋转轴路径光顺无法实现对刀轴方向转接误差的准确控制。此外,上述方法在拐角光顺过程中牵涉运动学变换,其计算效率存有进一步提升的空间。为此,Huang等[108]利用三次B样条曲线与单位球面投影策略,进一步提出了一种五轴刀具路径光顺方法,在保证刀尖点运动路径和刀具姿态运动G2连续同步的同时,也能够实现在工件坐标系下对刀轴方向转接误差的解析控制。由于PH样条曲线展现出的曲线参数与弧长之间的解析关系,最近Hu等[119]采用C3连续的PH曲线解析地构造过渡圆弧长度与样条曲线参数之间的联系,通过同步刀尖点运动和刀轴方向实现了加加速度约束下的五轴拐角光顺,所提刀具路径优化算法可以在开放式的数控系统中实现机床运动指令的实时插补。
2 多轴数控加工进给率规划策略
进给率规划作为运动轨迹控制的重要组成部分,在提高产品生产率,保证被加工零件表面质量以及加工精度方面起着至关重要的作用。合理地规划进给率,不仅能将曲面的加工轮廓误差控制在预设范围之内,也能够有效避免刀具磨损过快、崩刃、断刀等问题。根据加工约束的类型,目前的进给率规划方法大体可以分为3类:① 基于运动学约束的进给率规划,旨在通过规划进给率,对刀具沿轨迹移动时的瞬时速度、加速度、加加速度以及机床各分轴的速度、加速度及加加速度进行控制,从而提高数控加工过程的平稳性;② 基于几何学约束的进给率规划,旨在通过规划进给率,对多轴联动轨迹的静态逼近误差及动态轮廓误差进行控制,从而直接或间接地保证零件的加工精度;③ 基于切削力约束的进给率规划,其建立在动态切削几何-时变切削力仿真之上,通过规划进给率,对数控加工过程的切削力进行控制,以满足零件对表面层结构、内应力及表面形貌等特性的需求。本节将依据上述分类对进给率规划策略的研究进展进行论述。
2.1 基于运动学约束的进给率规划策略
光顺运动轨迹的产生不仅要求光顺的加工路径,还必须能够避免因加速度过大造成的刀具振荡、冲击等问题,因此刀具进给的运动学特性需要通过加减速算法进行控制。S曲线加减速算法[126-127]不仅能够对刀具进给的加速度进行控制,也能够将轨迹的加加速度限制在预设范围之内,能够有效克服传统线性加减速算法[128]和指数加减速算法[129]存在的加速度突变问题。因此,S曲线加减速算法在当前商用数控系统中得到广泛应用。针对传统S曲线加减速存在的加加速度不连续问题,Huang[130]、Wang[131]等利用正弦型曲线高阶导数连续性的特点,提出了加加速度连续的进给率规划方法,并取得了较好的实验效果。就控制对象而言,上述方法可统一归类为基于刀触点轨迹运动学约束的进给率规划方法。
由于刀具与工件间的相对运动是数控系统通过控制机床各驱动轴的协调动作来实现的。因此,除了刀具轨迹的运动学特性外,机床分轴的运动学性能同样对数控装备的加工性能产生重要影响。尤其是在五轴加工中,2个旋转轴的引入,在提高刀具的空间可达性的同时,也使得刀具轨迹的运动与机床各驱动轴的运动呈现复杂的非线性映射关系。即使刀具轨迹的运动学性能得到了很好的约束,机床分轴的加速度和加加速度依然有可能超出预设范围,影响零件表面的加工质量。为解决这一问题,Sencer等[132]利用基于弧长参数化的三次B样条描述刀具进给率曲线,推导出了机床各驱动轴速度、加速度、加加速度与进给率曲线控制点的非线性不等式关系,提出了基于序列二次规划的进给率优化方法。Zhang等[133]引入了速度限制曲面的概念,证明了各分轴加加速度约束下的进给率时间最优解需满足“Bang-Bang-Singular”控制结构,提出了一种基于贪心思想的进给率优化方法。Beudaert等[134]采用二分迭代算法将进给率规划从参数域优化问题转换到时域插值问题,并给出了基于前瞻策略的单变量数值优化方法(如图7所示)。此后,基于比例调整的多约束曲线演化算法[135]、双向扫描算法[136]、有限脉冲响应滤波算法[137]、动态启发式算法[138-139]等用于求解机床各轴驱动特性约束下进给率的方法也相继被提出。
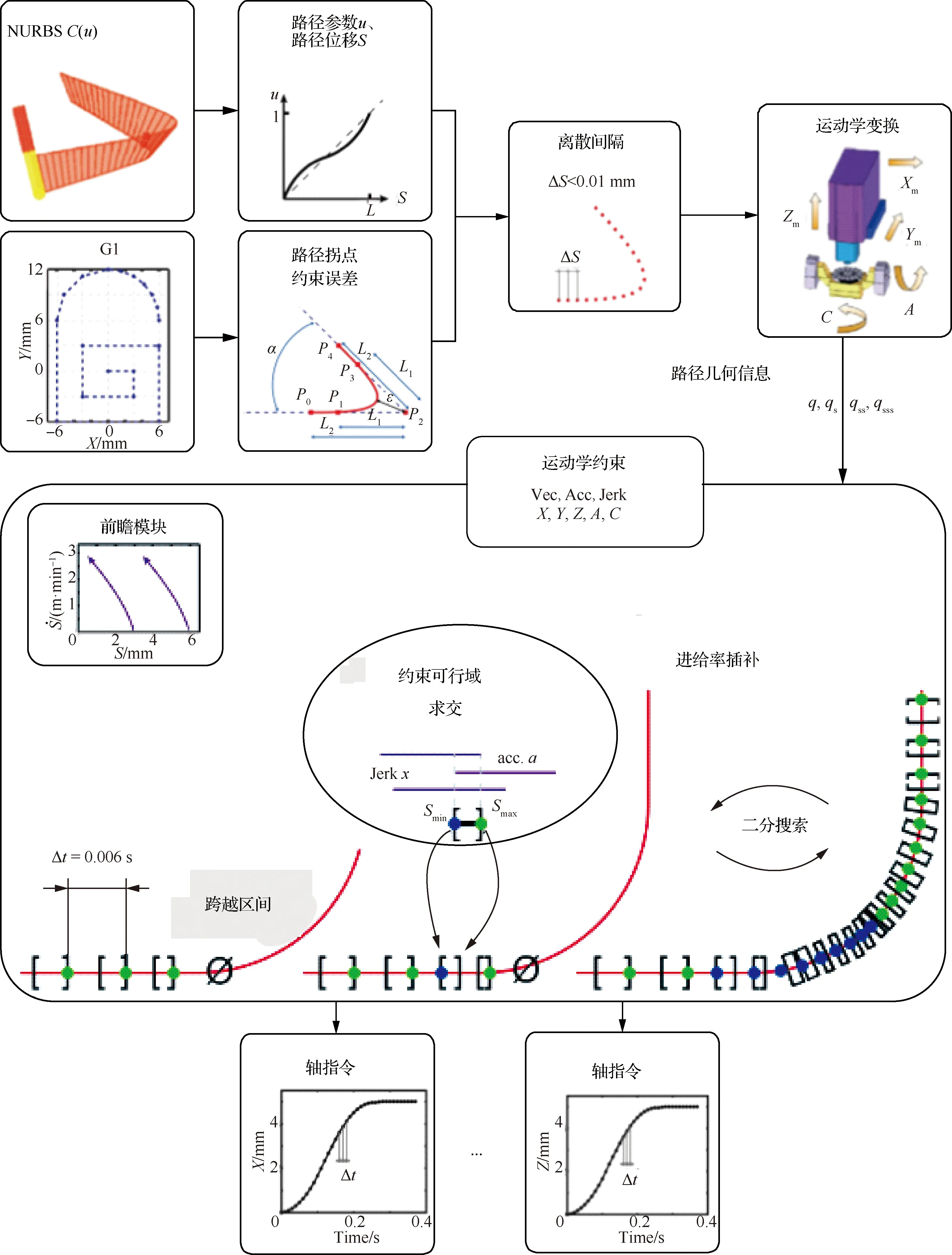
图7 基于二分迭代的时域插值方法[134]Fig.7 A dichotomy principle based time-domain trajectory interpolation method[134]
上述规划方法获得的进给率并不能保证是全局最优的,其计算效率也有待进一步提高。相比之下,线性规划算法凭借良好的计算鲁棒性和收敛性,受到了越来越多的关注。考虑到机床各轴加加速度与刀具进给率之间的关系难以直接线性化,目前基于线性规划的进给率规划策略通常是将进给率的平方值作为优化变量。例如,Fan等[140]采用放缩法建立了以加工时间最短为优化目标,以机床各轴速度、加速度和加加速度限制为约束条件,以进给率平方值为优化变量的线性规划模型,并通过数值求解方式获取了近似的全局优化解。在此基础上,Guo等[141]证明并推导了进给系统跟踪误差与进给率平方值之间的隐式关系。随后,针对长加工路径,Erkorkmaz等[142]融合并行窗口处理技术,给出了一种全局优化的两阶段进给率求解算法。最近,Sun等[143]给出了进给率与机床各轴驱动约束间非线性关系的线性化表达,提出了新的基于分段线性规划策略的进给率优化方法,率先将此类非线性优化问题转换为约束不等式求解问题。与现有方法相比,该方法能直接获得进给率曲线的解析表达,具有求解效率高、约束保证性好等优势。
2.2 基于几何学约束的进给率规划策略
与进给率规划密切相关的几何误差分为2类:即静态几何误差与动态轮廓误差,其中静态几何误差特指在轨迹粗插补阶段,由插补算法所引入的原理性误差,即弦高误差;动态轮廓误差是指数控加工中刀具的实际运动位置与理想刀位轨迹间的最小偏差,其误差来源主要包括伺服响应滞后、动态失匹以及外部干扰等因素。在几何误差约束下,规划进给率的核心在于对误差约束的准确建模。Yeh和Hsu[144]以弦高误差为约束条件,利用密切圆对理想轨迹的局部轮廓进行逼近,推导出了弦高误差极限值与进给率的二次显式表达式,提出了经典的自适应进给率规划方法。Du等[145]考虑空间曲线的挠率,采用锥形螺旋线代替密切圆,提出了具有三阶切触精度的弦高误差估算方法。相比于静态弦高误差,动态轮廓误差的建模与控制更为复杂。在动态响应匹配的假设下,Lin等[146]率先建立了以走刀进给率为自变量,以轮廓误差为因变量的非线性函数模型,通过求解六次方程获得满足轮廓误差约束的最大可行进给率的近似值。随后,Jia[147]、Wang[148]和Dong[149]等将整个位置闭环伺服系统近似为典型的二阶欠阻尼系统,分别给出了满足轮廓误差约束的最大可行进给率不等式条件,在简化求解难度的同时,也提高了求解效率。但上述方法只适用于三轴加工,受五轴系统非线性坐标变换的影响,很难直接应用于五轴加工。
在五轴加工中,除了需要对刀尖点轮廓误差控制外,还需对刀轴位向轮廓误差进行限制,如图8[150]所示。由于过大的刀轴位向误差不仅会造成曲面的过切和欠切问题,还会影响刀触点轨迹的控制精度。因此,五轴轮廓误差控制问题一直是多轴联动数控加工中的难点,但目前基于五轴轮廓误差约束的进给率规划研究依旧非常有限。为实现五轴轮廓误差的准确控制,必须解决如下2个关键问题:① 工件坐标系下刀位跟踪误差与关节坐标系下驱动轴跟踪误差间的非线性映射;② 走刀进给率与驱动轴跟踪误差、刀位跟踪误差及刀位轮廓误差间的非线性模型构建。针对五轴串联机床,Chen和Sun[150]基于伺服系统对插补指令信号的稳态响应,结合五轴机床坐标变换的雅克比矩阵,建立了进给轴跟踪误差在关节空间与曲面设计空间之间的线性映射关系,并利用曲线Frenet标架的微分运动关系式,推导出了五轴加工轮廓误差与走刀进给率间的解析关系,实现了对五轴加工刀尖点轮廓误差与刀轴位向轮廓误差的同步控制。针对高带宽数控系统,Yang等[151]深入研究了切削负载对五轴加工轮廓误差的影响,给出了大切削负载下的进给率求解方法。此外,离线增益动态调整法[152]、前馈指令修正法[153]、轮廓误差预补偿法[154]等也被相继提出,与现有进给率规划方法结合,能获得更好的加工效果。
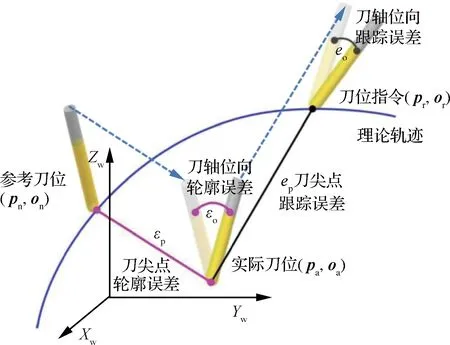
图8 五轴加工跟踪误差与轮廓误差示意图[150]Fig.8 Schematic diagram of tracking error and contouring error in five-axis machining[150]
2.3 基于切削力约束的进给率规划策略
对切削力的精确控制能够有效提高表面加工质量、减少刀具磨损、降低加工能耗,而在影响切削力的相关工艺参数中,进给率起着非常重要的作用。尽管目前多数商用CAM系统集成了进给率优化模块,但多数都是基于恒定材料去除率模型的进给率优化。由于其只考虑了切削过程的材料去除体的变化,并未考虑刀具-工件的材料属性以及加工过程相关物理量的变化,并不能准确地反映实际的切削过程。最近研究结果证实,切削力约束下的进给率规划策略能有效缩短加工时间、提高加工效率(如图9所示)[155],此类方法已逐渐受到人们的重视。例如,针对三轴点铣加工,Guzel和Lazoglu[156]基于Z-map离散几何模型提出了一种离线分段进给率规划方法,以提高数控加工效率。Erdim等[157]分析了不同刀具进给模式下刀具-工件切触区域的变化,给出了新的瞬时未变形切削厚度计算方法并引入了基于比例修正的进给率优化方法,能够实现加工过程的恒力铣削。随后,Ko和Cho[158]、Kim等[159]分别针对整体立铣刀与可转位立铣刀的铣削工艺,考虑刀具跳动、变形的影响,提出了近似时间最优的进给率求解方法。此外,Feng和Su[160]将路径优化与进给率规划结合,提出了一种以走刀进给方向为优化变量,以加工效率最大为优化目标的多约束集成算法。考虑数控加工过程的随机性,Zhang等[161]针对锻/铸件粗加工工艺,也给出了一种基于实测切削力修正的进给率规划方法,避免了机械切削力模型的系数标定,简化了求解过程。
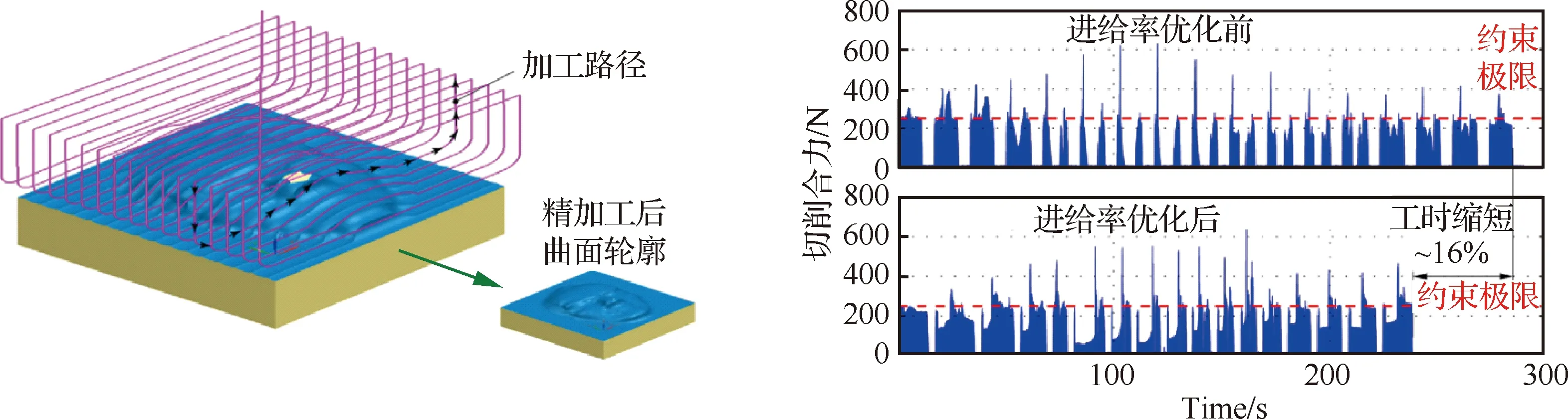
图9 切削力约束下进给率优化前后的切削力及加工时间对比[155]Fig.9 Comparison of resultant cutting forces and cycle time before and after feedrate scheduling considering constraints of cutting forces[155]
针对多轴侧铣加工,Ko等[162]通过调整控制器内置加减速时间,提出一种基于虚拟加工技术的离线进给率规划策略,保证了其算法在实际工程应用的可行性。Xu和Tang[163]通过引入切削力-切触区域商函数的概念,提出了新的五轴轨迹生成算法,该算法在能够提升可行进给率极限值的同时,也能有效地将切削力控制在给定阈值之内。然而,为了实现切削力的精确控制,上述方法往往需要经过多轮迭代才能获得最终的进给率优化解。针对这一问题,Wang等[164]基于最小二乘原理,建立了以刀具切入角和进给率为变量的瞬时未变形切削厚度解析计算模型,给出了五轴侧铣加工切削力峰值的快速提取方法,以此为基础提出了恒定峰值切削力的进给率规划方法,能有效提高五轴加工进给率规划效率。
3 复杂曲面零件多轴数控加工动力学
航空复杂曲面零件多为钛合金、高温合金等难加工材料,材料去除率高,铣切量占毛坯重量的90%以上,而且结构刚性弱、阻尼小,面型/廓形复杂,对尺寸精度和表面粗糙度也有极高的要求。这使此类零件在铣削过程中极易发生变形、强迫振动及自激颤振,如何实现其高效稳定加工就成为亟待解决的制造技术难题[165]。与传统三轴加工过程不同,复杂曲面零件在五轴联动加工过程中,刀具-工件的啮合关系随刀轴矢量变化,切削力波动剧烈[166];“机床-刀具-工件-夹具”工艺系统的动态特性随材料去除和机床位姿时变[167-168],加工动力学模型不再是定常系统;极端弱刚性工件在切削激励作用下的振动幅值可达几十至几百μm,变形与振动对名义切削用量的影响不可忽略[169],自激颤振机理呈现出多重再生的特点[170],原有单重再生动力学模型不再适用;工艺系统的动力学行为也更加丰富,信号特征发生了很大变化[171];此外,五轴加工过程中刀轴矢量的连续变化给抑振刀具设计[172]、进给与转速调控[173]等颤振抑制策略的应用带来了极大的困难。考虑到目前航空复杂曲面零件铣削动力学相关研究仍遵循着“动力学建模—动态响应分析—颤振抑制与调控”的思路,本节将分别从上述3个方面概述其主要研究进展。
3.1 铣削动力学建模
铣削动力学模型反映了工艺与装备之间的复杂交互作用,一般采用“质量-弹簧-阻尼器”集中参数模型来表示[174-175],在数学形式上呈现为二阶时滞微分方程,其表达式为
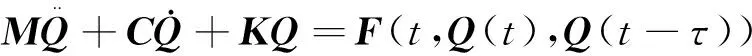
(1)
式中:M为质量矩阵;C为阻尼矩阵;K为刚度矩阵;Q为振动向量;F为切削力;t为时间;τ为时滞参数。
对于航空复杂薄壁曲面零件,上述动力学方程在模型精度和适用范围方面存在很大局限,而建立准确的“工艺-装备”系统动力学模型是进行动力学分析的基础和实现无颤振高性能加工的前提,因此近年来的诸多工作均是围绕如何提升动力学建模的准确度开展。在系统动态特性辨识方面:为考虑五轴联动过程中机床位姿对刀具端动态特性的影响,张俊等采用子结构导纳耦合分析实现了双摆头型机床不同位姿下的刀尖频响快速预报[168]。为表征材料去除和刀具-工件切触位置变化对工件端动态特性的影响,Budak[176]、Yang[177]、Tuysuz[178]等相继提出了结构动力修改、生死单元、降阶子结构等方法进行工件实时频响预报,但由于工艺系统的阻尼特性难以计算求取,上述方法在生产实际中的应用尚面临较大挑战。在动态切削力建模方面:Kilic和Altintas[179]按照力的成因将切削激励力分解为进给作用产生的剪切力、再生效应导致的剪切力、刀刃及后刀面犁切作用产生的犁切力和切削速度相关的过程阻尼力4部分,其表达式为
(2)
五轴加工过程中,刀具-工件之间切触关系随刀轴矢量变化,刀具-工件啮合区域和瞬时未变形切厚难以解析求取,国内外学者先后提出了Z-map[180]、Z-buffer[181]、实体法[182]、球族包络法[183]等方法进行五轴切削力建模。此外,薄壁弱刚性零件在切削激励作用下的变形量和振动幅值在量级上与切削厚度相近,工艺系统动态响应对名义切削用量的影响不可忽略,作者团队[169]考虑变形与切削几何的耦合关系,实现了薄壁件动态切削力的精确求取。Rubeo和Schmitz[184]推广Tlusty提出的“再生切削力,动态变形”模型,利用基于初值的时域仿真方法实现了更为精确的动态切削力建模和薄壁件稳定性判别,但尚未应用于五轴薄壁曲面零件。
3.2 动态响应分析
铣削加工动态响应分析可分为稳定性分析和加工质量评价2部分。铣削稳定性分析的目的是在已有加工动力学模型的基础上判断采用当前工艺参数加工是否会发生颤振。目前,铣削稳定性分析方法大致可分为3类:① 频域法,如零阶频域法[185]、多阶频域法[186];② 时域半解析法,如半离散法[187]、全离散法[188]以及数值积分法[189];③ 基 于初值的时域仿真法,如切削力峰谷值波动幅度法[184]。航空复杂薄壁曲面零件铣削加工的径向切深小,切削激励呈现出强间断冲击的特点,高阶频谱成分多,因此基于Fourier级数展开与截断的频域稳定性分析方法精度有限,半离散法等多数时域仿真半解析法在刀具回转周期上采用等间距离散策略构造状态转移矩阵,刀齿在切削时段内的有效离散份数少,严重影响了计算精度;时域仿真法采用逐步积分的方式对响应输出(切削力、振动位移等)进行时间历程分析,便于考虑大幅振动造成的刀具跳出等非线性因素,但计算效率极低,严重制约了算法在实际中的应用。此外,刀具跳动、加工变形和切削振动耦合作用下的薄壁件铣削颤振呈现出多重再生的特点[170],时滞动力学模型存在强非线性因素,频域法和时域半解析法难以直接适用。
稳定性分析只提供了切削参数“稳定”或“颤振”简单二元评价,无法直接衡量加工精度,而稳定区域内不同的切削参数对应着不同的振动响应,即不同的表面位置误差与表面粗糙度,因此需要以加工质量为衡量指标对动态响应进行多元评价。Niu等[190]推广半解析判稳方法实现了颤振稳定性、表面位置误差和表面粗糙度三者同步高效预报,如图10所示。Bachrathy等[191]建立了刀具端振动位移与加工精度之间的映射关系。Mann等[192]基于不动点理论推广半解析判稳方法实现了表面位置误差预报。然而现有方法多是针对三轴铣削加工,有关复杂薄壁曲面零件的动态响应分析则鲜有报道。
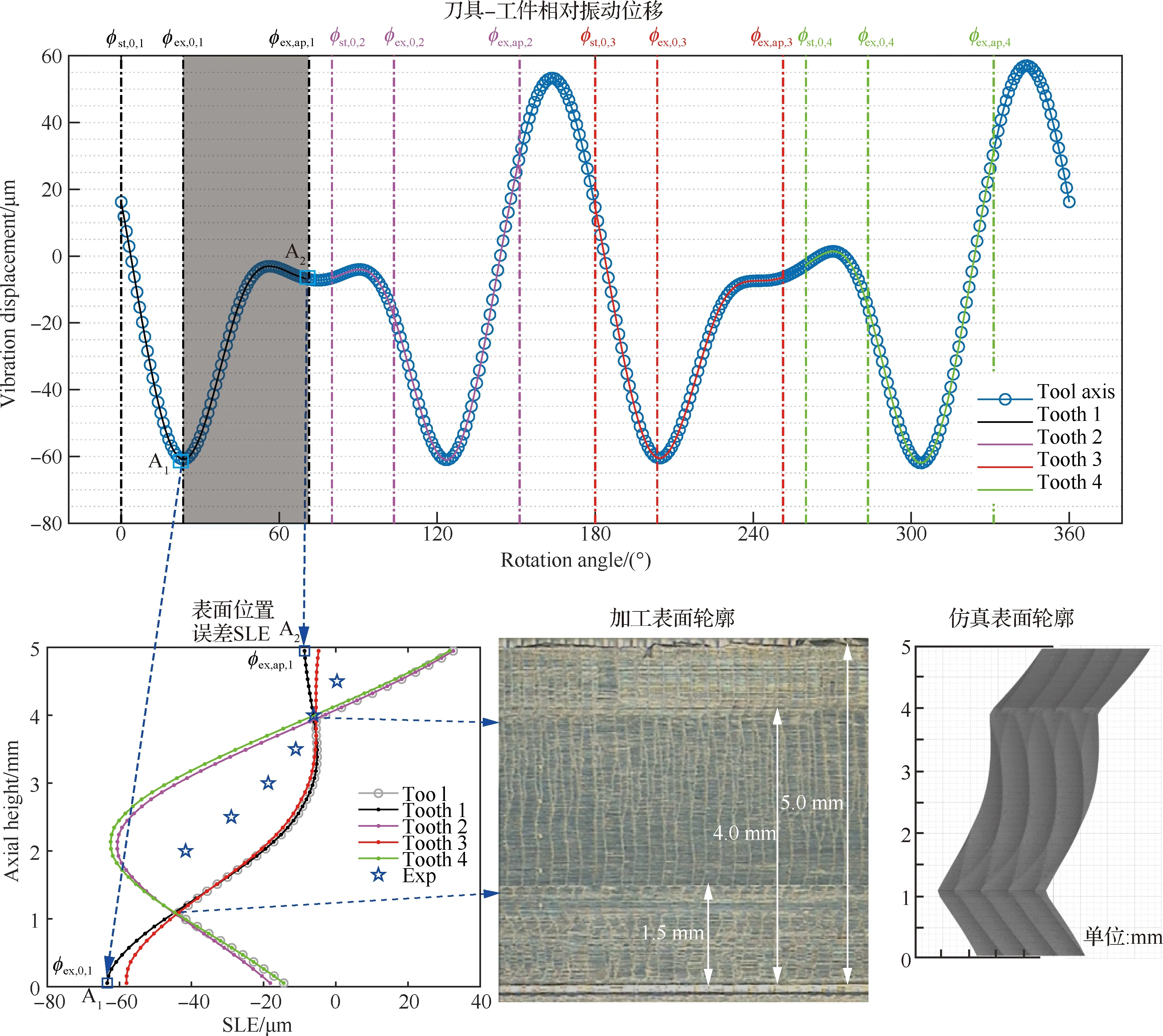
图10 基于动态响应分析的铣削加工表面形貌仿真[190]Fig.10 Simulation of surface topography based on dynamic response analysis of milling system[190]
3.3 颤振抑制与调控
薄壁件铣削颤振抑制与调控策略主要包括工艺参数优化策略和阻尼/刚度增强策略2种。依据稳定性Lobe图合理选取工艺参数是规避铣削颤振最常见的方式。由于薄壁工件在铣削过程中动态特性随材料去除及刀具切削位置变化,传统的“主轴转速-轴向切深”二维稳定图不再适用,Jin[193]、Yan[194]、Yang[177]等分别采用不同方法在“主轴转速-刀具位置-轴向切深”三维参数空间绘制了稳定边界,通过合理选取工艺参数实现了颤振避免。但薄壁工件因自身弱刚性导致切削稳定域十分狭小,单纯依靠三维稳定图选取切削参数的策略加工效率十分受限。
由于薄壁件铣削动力学模型为时滞微分方程,时滞大小由主轴转速和刀具几何共同决定,因此可以通过时滞调控策略扩大工艺参数的选取范围,Buransky等[195]实验发现采用不等齿距铣刀可扩大稳定域并改善薄壁件表面质量,Budak[196]、Zhan[172]等证实不等齿距铣刀可以提升五轴铣削稳定极限。不等齿距铣刀颤振抑制属于多时滞调控,Niu等的研究工作表明采用变螺旋角铣刀[170](分布时滞调控)或主轴转速连续调制[173](变时滞调控)同样可以改变再生颤振的发生机制,从而起到颤振抑制作用,而且调控方式更为灵活,但分布时滞调控与变时滞调控策略尚未推广至复杂薄壁曲面加工。
低机械阻抗特性导致的稳定域狭小是薄壁件铣削工艺系统的固有属性,通过引入辅助支撑和耗能装置可提升工件端的刚度和阻尼,从而达到改善薄壁件铣削加工稳定性的目的。Aoyama和Kakinuma[197]采用圆柱支撑点阵显著提升了薄壁件工艺系统的机械阻抗。Geng等[198]采用空气弹簧增强了圆筒形机匣的工艺刚度。Shi等[199]通过在薄壁件局部贴附约束阻尼层,将薄板的加工振幅减少了80%。Kolluru和Axinte[200]证明,同时采用刚度增强和阻尼增强策略具有更好的颤振抑制效果。作者团队[201]设计了用于航空发动机机匣减振提效的自动化夹具,如图11所示。
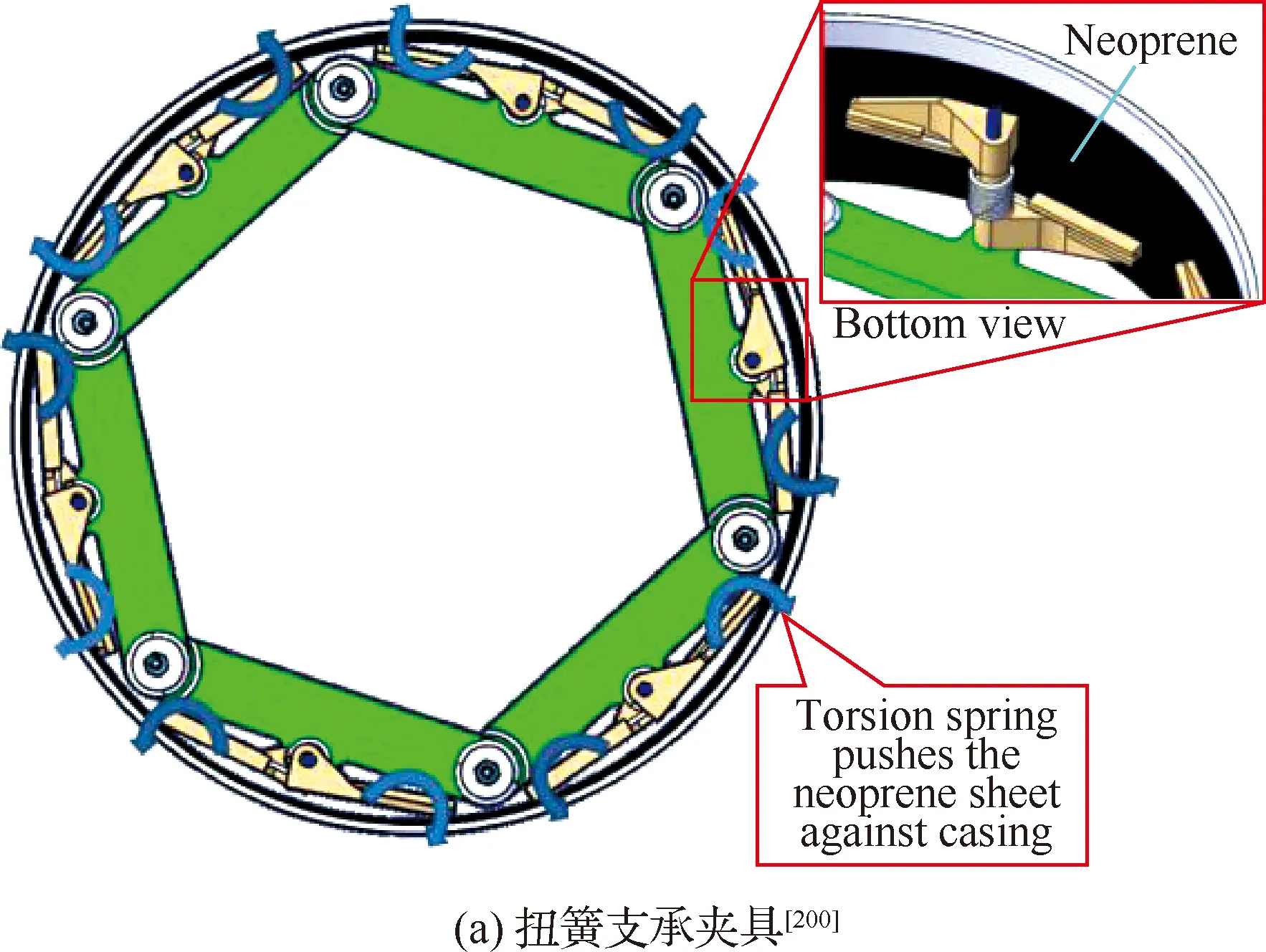
图11 航空发动机机匣减振支承夹具Fig.11 Damping fixtures for aero casing
4 结论与展望
目前数控加工相关技术的研究在加工路径设计、进给率规划、动力学分析等方面取得了较大进展,但仍难以满足精密复杂曲面零件的高性能制造需求,存在的不足和未来发展趋势归纳如下:
1)传统刀轨设计方法仍拘泥于单纯几何学层面的逐点轨迹设计、排布形式依赖于初始路径的选择,从几何学、运动学及切削特性综合层面考虑刀具轨迹拓扑几何形状的方法较少,无法兼顾曲面几何物理特性、难以实现刀具轨迹的整体调控。需要借助最近提出的走刀矢量场的概念,构造能够准确反映切削带宽最大、进给速度最快、动力消耗最少、实现薄壁件变形控制、切削载荷均衡以及表面气动特性等设计加工意图的各类走刀矢量场,建立能够融合几何物理特性的走刀流线场的整体表达,形成局部走刀方向与整体路径排布兼顾的刀具轨迹设计新模式,突破传统方法无法兼顾几何、切削特性及曲面物理性能的局限。
2)数控加工是一个复杂的物理过程,刀具姿态确定不仅要从几何学层面考虑零件表面加工精度、避免刀具局部干涉和全局碰撞,其规划也受到相邻刀触点甚至整条刀具轨迹上刀具姿态变化的限制,必须考虑刀具姿态变化的光顺性以及刀具姿态变化与机床运动学性能及加工过程动态切削特性之间的关系。目前,刀具姿态优化的研究正逐渐从保证刀具运动几何可行的干涉碰撞消除、机床驱动轴的运动平稳光顺,向加工过程几何与运动学约束下的切削特性改善方向发展。五轴加工刀具姿态优化与路径光顺必须综合考虑数控加工过程中的几何学约束、奇异性限制、运动学性能以及切削力、加工变形及颤振等动态切削特性的影响,才能充分发挥高档数控机床加工潜能,提高复杂曲面零件的加工效率及成形精度。
3)在多轴联动加工进给率规划方面,受时变切削条件、机床几何误差位置/时间相关性以及诸多非线性不确定因素的影响,曲面成形误差与走刀进给率之间的关系难以用准确的数学模型来描述,刀具磨损、零件表面物理性能与工艺参数间的潜在关系尚未探明,针对多元扰动下的伺服驱动系统的动态响应特性研究尚未开展,换言之,以进给率为参考的工艺规划系统在建模层面还存在很多尚未解决的问题。此外,目前基于五轴参数路径的进给率规划研究依旧停留在离线模式,对于高精密复杂曲面类零件数控加工,其拓展性差、重用性低的算法架构,难以满足实时性强、容错率高的现场需求,离工程应用还存在较大差距。因此,如何实现CAM/CNC加工路径信息的无缝集成,开发具有兼容性好、鲁棒性强的进给率插补,对发展新一代高性能精密数控加工系统具有非常明确的现实意义。
4)在工艺系统完整动力学建模方面,尚未厘清减振支承与耗能装置对工艺系统工件端输出阻抗的影响规律,尚未探明变形与振动反馈作用下,薄壁曲面零件五轴联动加工再生颤振的发生机理,因此没有建立起完整的“支承-工件-刀具-机床”工艺系统动力学模型。由于加工变形、振动与动态切削力存在强耦合关联关系,薄壁曲面零件的加工动力学方程也因此呈现出强非线性,现有的稳定性分析方法难以适用,因此如何精确高效地建立起工艺系统动态响应与加工质量的映射关系,并建立加工质量导向的工艺优化反演模型是一个非常值得研究的问题。单纯依靠工艺参数优化或单纯依靠减振支承与耗能装置进行航空复杂薄壁曲面零件的颤振抑制均存在一定的局限性,现在尚未建立起“支承-工艺”协同抑振的理论体系,航空复杂曲面零件的高效精密加工缺乏足够的理论支撑。
