基于球谐变换的GERD水库形变预测

刘慧玲 陈 雨 王希禾

1 四川大学电子信息学院，成都市一环路南一段24号，610065

水坝通过调节水流，为人类和环境的各种需求提供了可靠水源[1]。埃塞俄比亚的文艺复兴大坝(Grand Ethiopian Renaissance Dam，GERD)是现今非洲最大的大坝，预计其有效库容可达74 km3[2]。GERD水库蓄水将引发大量的水文迁移，可能导致周边地区发生大规模的地表形变[3]，地表形变量超出一定界限会演变成为地质灾害，对人类生命和财产安全带来严重损失[4]。

地表形变监测网络是监测区域地表形变的有效方法之一[5]，但该方法不适用于GERD水库区域，因为GERD附近240 km范围内没有可用的GPS站点，距离GERD 142 km的ASOS站点已于2017年停止工作。卫星遥感可以进行长时间、高覆盖率的观测，能连续监测水库蓄水和地表覆盖变化，许多研究者利用多种遥感数据相结合成功估算了特定地区的地表形变[6-7]。GRACE以及最新的GRACE-FO三大数据处理机构(JPL、CSR、GFZ)将地表引力场变化通过球谐变换，得到随时间变化的GRACE重力数据的球谐系数(spherical harmonic coefficients，简称SHC)形式(即Level 2产品)[8]，利用该产品并引入负荷勒夫数(Love numbers)可反演得到相应重力变化引起的地表负荷形变[9]。但由于GRACE的分辨率只有200～300 km，其时变重力场的SHC的阶数只能展开到60～96阶[10]，受制于分辨率的影响，大部分研究中基于GRACE反演得到的地下水储量变化与实际结果的相关系数仅为0.6～0.7[11]。所以，通常利用GPS数据或其他水文模型对GRACE反演后的结果进行校正。

根据以上分析，本文基于球谐变换和Love numbers提出一种预测GERD水库蓄水引起的地表形变的方法。首先假设3种蓄水方案：短期5 a、中期10 a、长期15 a内注满74 km3的水库，并根据数字高程模型(DEM)分别对3种蓄水方案中每月蓄水表面积、体积和平均水高进行数字拟合。然后以平均水高为基础创建一个7 200×3 600的栅格网络，该栅格水库区域的各点设为平均水高值，水库区域外各点设为0。通过对比等效水高(equivalent water height，EWH)和平均水高分析高阶球谐截断所造成的信号能量损失，再以2 300阶的球谐变换系数为基础，通过引入Love numbers计算水库及周边区域的垂直和水平形变。

1 数据准备和研究方法

1.1 研究区域及数据准备

GERD位于埃塞俄比亚的蓝色尼罗河上，地处苏丹和埃及的上游，于2011-04开始建设，计划正常水高为640 m，水库蓄水体积为74 km3，约为大坝所在地年均流量的1.5倍[12]。

采用美国宇航局的SRTM-DEM数据(https:∥dwtkns.com/srtm30m/)，空间分辨率为30 m。根据GERD的实际位置先选取32°50′～48°9′E、3°21′～ 15°1′N的区域，然后将GERD的位置作为倾泻点，从上述区域中划分出本文的研究区域——上蓝色尼罗河流域。

1.2 研究方法

本文的数据处理流程分为5个步骤(图1)：1)利用SRTM-DEM数据对研究区域在不同蓄水策略下提取的水体进行分析，得出蓄水过程中每月水库的蓄水表面积、体积和平均水高；2)构建全局栅格图，将水库区域内的栅格值设为当月平均水高，其余区域设为0；3)将此栅格网络球谐扩展为最大谐波度(Nmax)分别为60、700、1 500、2 300的SHC；4)利用SHC计算EWH，先通过比较EWH和平均水高，分析高阶SHC对信号能量损失的影响，再利用Nmax=2 300阶时的SHC计算地表形变；5)提取垂直、东、西、南和北向形变的时间序列图。

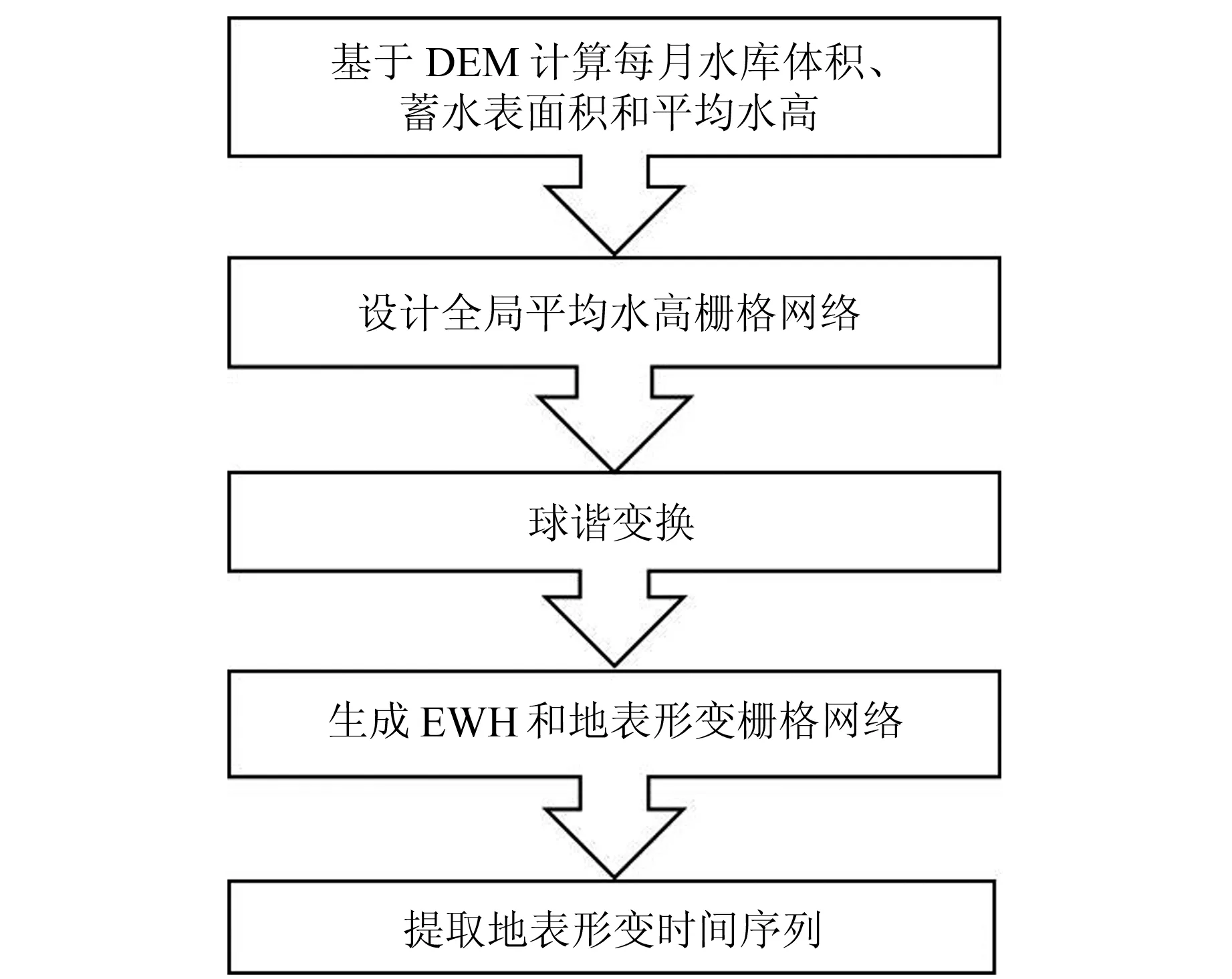
图1 数据处理过程Fig.1 Data processing

1.2.1 计算水库蓄水表面积、体积和平均水高

首先使用一组高程值间隔1 m的水平表面截取研究区域的SRTM-DEM栅格图，获得指定存储层中每个水平表面下的体积，再构建以体积为自变量的体积/水平面高程值拟合函数。如果以74 km3作为水库额定容量，将蓄水年限分为5 a、10 a和15 a分别进行计算，对于3种年限，每月分别需蓄水1.23 km3、0.61 km3和0.41 km3。利用体积/水平面高程值拟合函数计算不同蓄水策略下每月蓄水体积对应的水平表面高程值；然后使用ArcGIS工具计算水库存储层中每月水平表面高程值下的蓄水表面面积；最后用月蓄水体积除以蓄水表面积得到每月平均水高。

1.2.2 设计平均水高栅格及球谐展开

本文构建了一个分辨率为0.05°×0.05°的包含全球经纬度的栅格网络。水库范围内的栅格值设为当月平均水高，其余栅格值设为0；然后将此全局栅格网络球谐展开至指定Nmax的SHC，并根据Wahr等[13]的方法求出每月变化量。

1.2.3 计算EWH和地表形变

利用球谐函数计算EWH和地表变形时需引入Love numbers，每月SHC变化量结合Love numbers可计算由水文质量载荷变化引起的EWH变化和3D位移。ΔEWH的具体计算公式可参考文献[14]，3D位移的具体计算公式可参考文献[15-16]。

2 结果分析

2.1 每月水库蓄水表面积、体积和平均水高

图2是5 a、10 a和15 a蓄水策略的模拟实验中水库蓄水表面积和平均水高随时间变化曲线。由图可见，3种蓄水策略下GERD水库平均水高的月平均变化量分别为1.63 m、0.88 m和0.61 m，水库蓄水表面积的月平均变化量分别为28.66 km2、14.59 km2和9.72 km2。

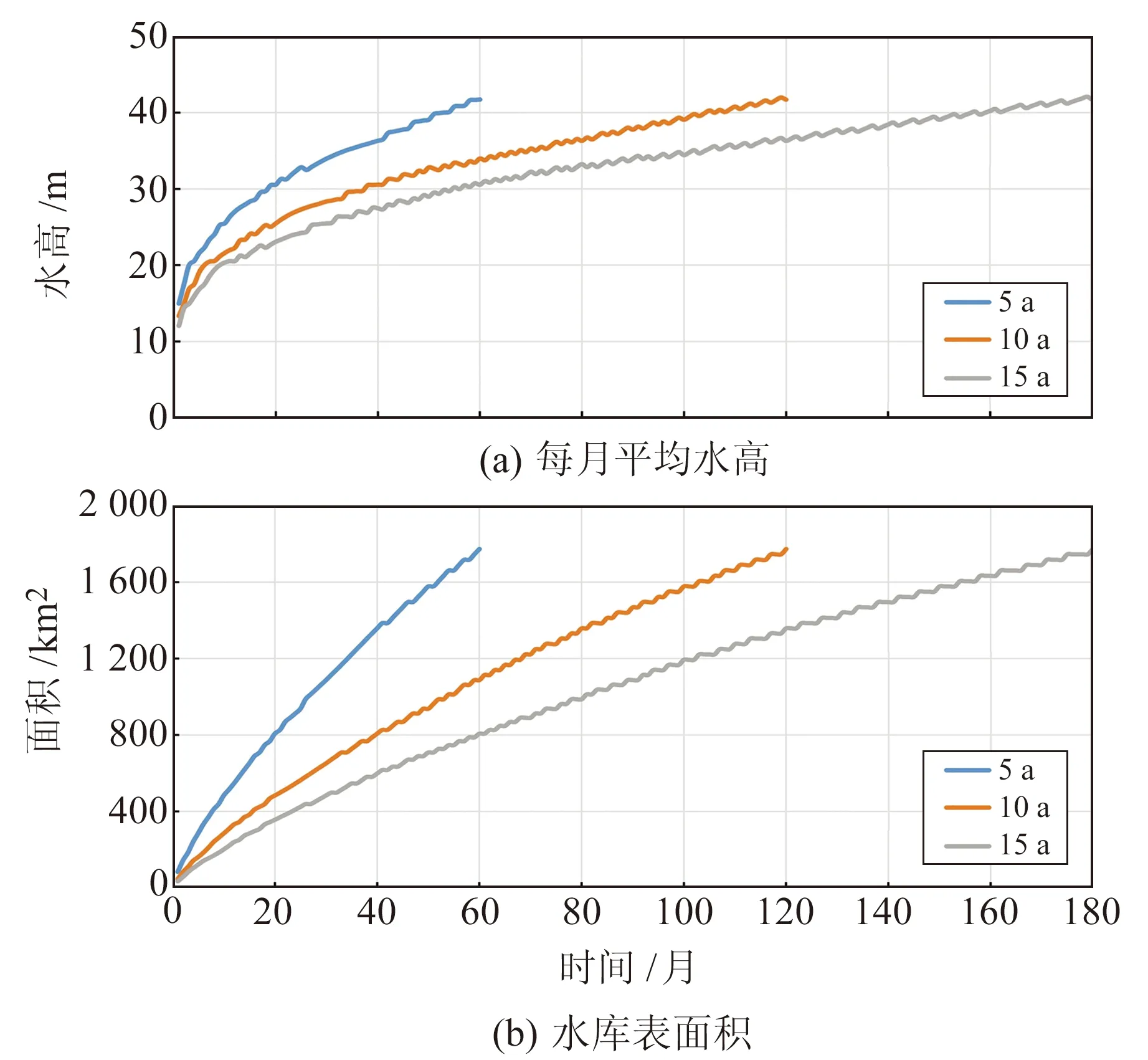
图2 3种策略下每月平均水高与水库表面积Fig.2 Monthly average water height and area under three strategies

图3为3种蓄水策略在不同蓄水阶段的体积、蓄水表面积和水位的变化。分析可知，5 a策略的第1个月蓄水体积为1.23 km3，其水面面积为82.52 km2，平均水高为14.96 m；10 a和15 a蓄水策略中对应的数据为0.61 km3、46.05 km2、13.32 m和0.41 km3、34.11 km2、12.06 m。当5 a 蓄水策略完成时，10 a蓄水策略完成50%，15 a蓄水策略完成约33%；当10 a蓄水策略完成时，15 a蓄水策略完成约66%；当整个蓄水完成时，会形成一个体积约为73.99 km3、面积约为1 773.2 km2、平均水高约为41.72 m的水库。

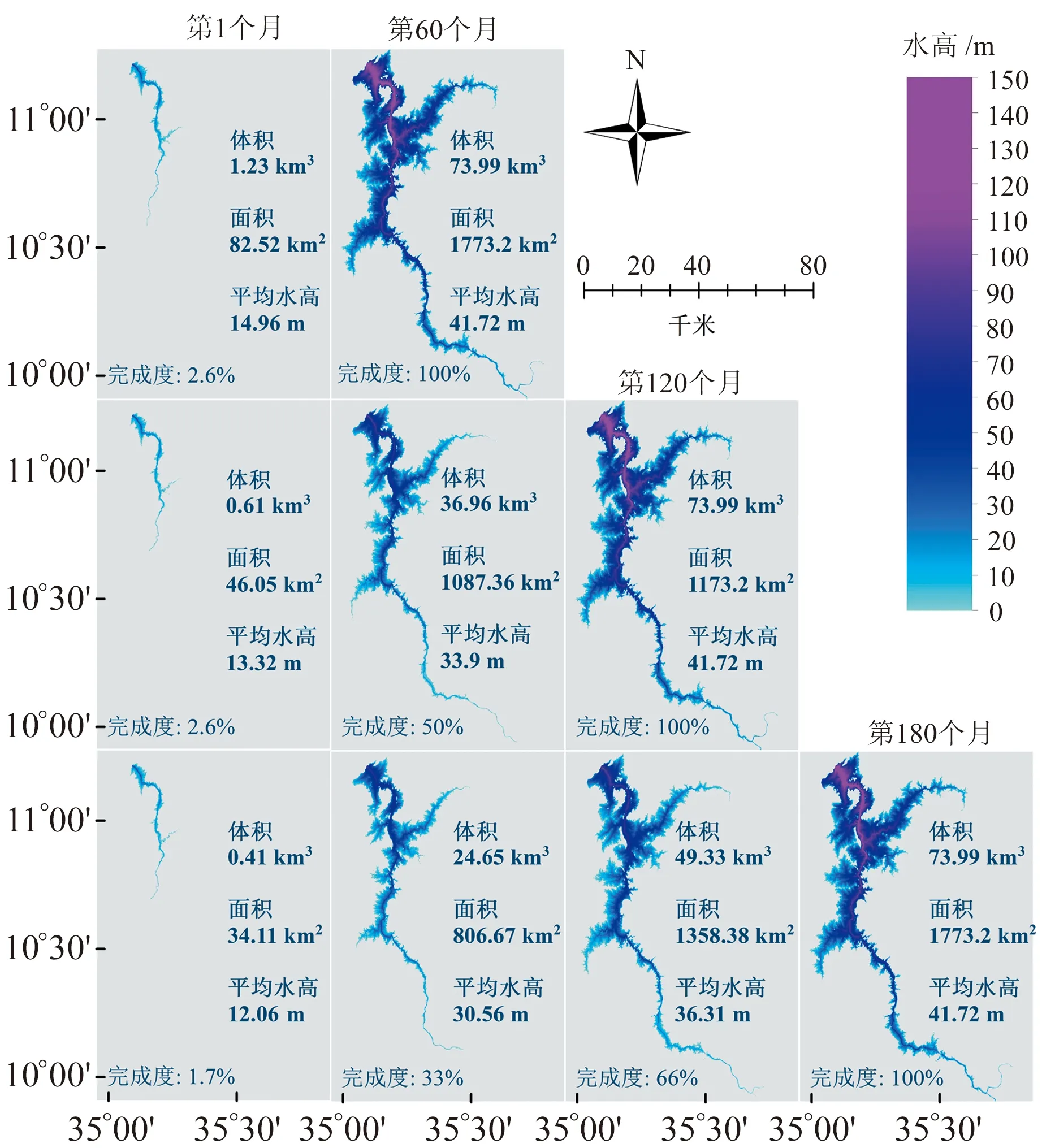
图3 3种策略模拟水库容量、水位、面积Fig.3 Simulated reservoir volume, area and water height using three strategies

2.2 基于不同Nmax的EWH对比与分析

图4(a)为5 a蓄水策略中第30个月的平均水高图，水库内的栅格值为34 m(蓝色区域)，水库外栅格值为0(黄色区域)。在此蓄水阶段中，根据不同Nmax计算各自的EWH，结果如图4(b)～4(e)所示。

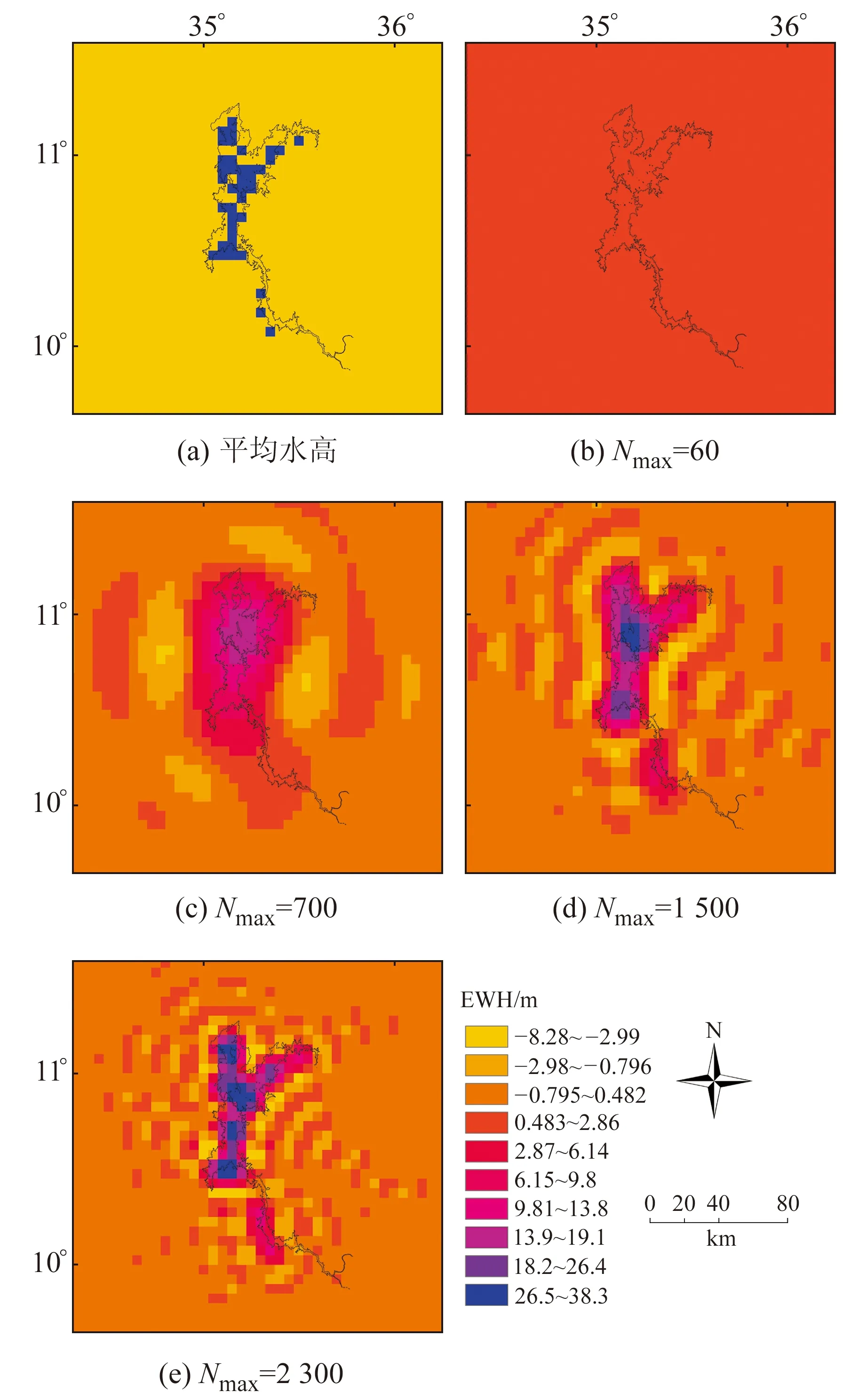
图4 5 a蓄水策略下第30个月的平均水高与EWHFig.4 Average water height and EWH of the 30thmonth under 5 a filling strategy

Parseval能量守恒定理表明，信号在空间域的平均功率等于时域中各次谐波分量的平均功率之和[17]。虽然Parseval定理通常用于描述傅里叶变换的统一性，但该特性的最一般形式应更恰当地被称为Plancheral定理。在数学中，Plancheral定理是谐波分析的结果，所以能量定理也适用于谐波分析。当研究区域为面积较大的水库或湖时，区域地表质量变化的主要影响因素是水库或湖中水的储量变化。研究中常用ΔEWH(θ,φ)来表示陆地水储量的变化[18]。

由于球谐扩展受Nmax的限制，高阶谐波被截断导致信号在空间域被平滑和扩展，所以利用球谐函数计算ΔEWH和3D位移是一种数值再分配模式下的计算，计算后的区域比研究的水库区域要大得多。图4(b)显示了由于高于60阶的谐波信号被截断导致信号能量被平滑、衰减和扩展至水库边界之外的现象，其栅格单元中EWH的范围为-0.164～0.123 m。

随着Nmax的逐渐增大，受截断效应影响的信号逐渐减少，EWH信号向GERD水库中心集中，呈现出水库中心区域的EWH值明显大于周边区域的特性。当Nmax=700，水库中心区域的EWH最大值为16.5 m，EWH的范围为-3.2～16.5 m；当Nmax=1 500时，水库中心区域的EWH最大值增加至30.03 m，EWH的范围增加至-3.83～30.03 m；当Nmax=2 300时，已显示出了EWH沿GERD水库区域分布的特性，EWH的范围为-8.28～38.3 m(由于吉布斯现象会出现少数大于34 m和小于0的栅格值)。

利用Nmax=2 300时的SHC计算5 a蓄水策略下的平均水高与EWH的时间序列。经误差分析，两者的平均相对误差仅有1.6%，因此选定Nmax=2 300阶计算后续地表形变。

2.3 地表形变及其时间序列

2.3.1 垂直形变

计算5 a策略中第30个月的垂直形变，结果如图5(a)所示。从图中可以看出，栅格中所有质量载荷点的垂直位移分量都向水库质心运动，为负值。该月垂直形变位移的范围为-91.13～-0.49 mm,且越靠近水库区域垂直形变位移量越大，水库中心区域的垂直形变位移范围为-91.13～-55.04 mm。

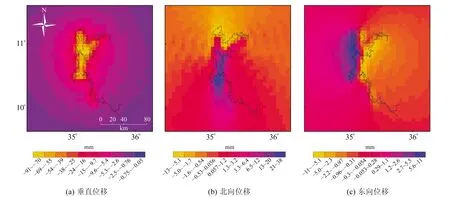
图5 5 a蓄水策略下第30个月的形变结果Fig.5 Deformation results of the 30th month under 5 a filling strategy

2.3.2 水平形变

水库区域质量载荷点的位置决定了该点的位移方位(向北或向南)，由于水库北部面积大于南部，因此质量载荷在南部单元上产生的拉力大于北部。在5 a策略下第30个月的蓄水阶段中，南向位移的最大值约为9 mm，北向位移的最大值约为37 mm。另外，由于水库北部区域较宽，因此东部和西部的单元也包含了向南移的分量，如图5(b)所示。

东西向位移与南北向位移相似，水库西岸的载荷点运动趋势向东，表现为正值，水库东岸的载荷点则向西移动，表现为负值，如图5(c)所示。由于GERD水库东西方向分布较为均匀，所以呈现的东西向位移量也较为均衡，东向位移的最大值为9.31 mm，西向位移的最大值为10.59 mm。

2.3.3 地表形变的时间序列

依据图5的结果分析垂直向、南北向和东西向的形变区域，并计算3种蓄水策略下5个方向的时间序列，结果如图6所示，图中，V表示垂直形变，E表示东向形变，W表示西向形变，N表示北向形变，S表示南向形变。

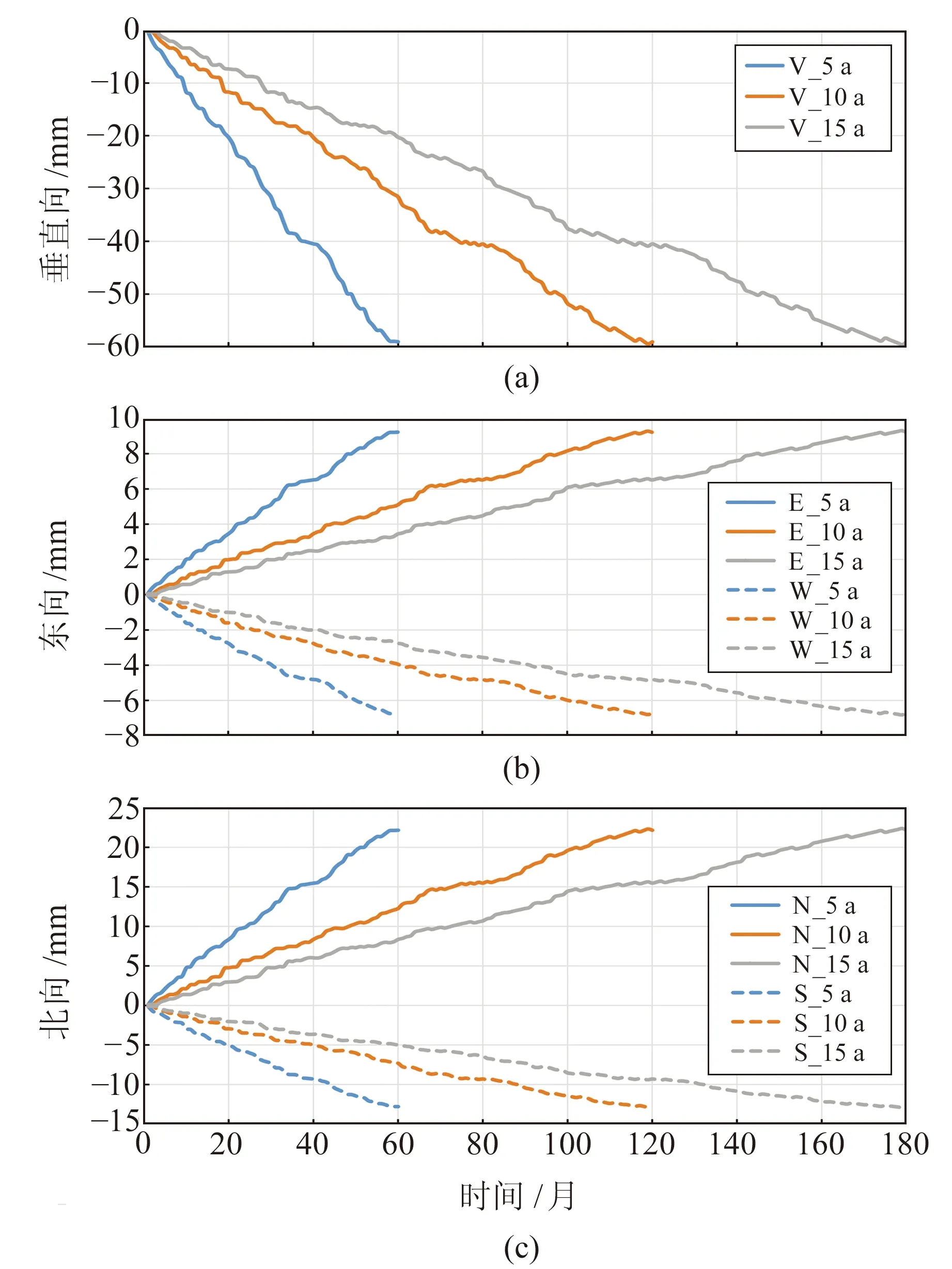
图6 3种蓄水策略下水平形变的时间序列Fig.6 Time series of horizontal deformation under three strategies

使用恒定体积的水蓄满水库时，蓄水初期和中后期将产生较大的垂直位移, 5 a策略下垂直位移变化的最快速率和最慢速率分别为1.2 mm/月和0.4 mm/月；10 a策略下对应速率降为1.0 mm/月和0.35 mm/月；15 a策略下仅为0.45 mm/月和0.2 mm/月。这3种策略的年平均垂直位移量呈递减的趋势，分别约为11.8 mm、5.9 mm、3.9 mm。

如图5(c)所示，5 a蓄水策略下第30个月的东西向位移网格图显示出一定的对称性；这种对称性在东西向位移的时间序列中也有体现，如图6(b)所示。本文认为，这种对称性是由于水库东西狭窄的形状所引起的。5 a策略的东向年平均位移量约为1.8 mm，最快的变化发生在蓄水的第9个月，达到0.42 mm/月，在蓄水的最后时期，移动速率降到0.1 mm/月；10 a策略下最快和最慢的东向位移速率为0.35 mm/月和0.07 mm/月，分别发生在蓄水期的第19个月和第80个月前后；而在15 a策略下，东向形变最大速率为0.25 mm/月，最小速率为0.03 mm/月。

GERD水库南部和北部质量分布不平衡导致南部和北部的位移分量趋势不同，北部较大的区域可能会分散质量负荷，北部质量载荷单元的移动小于南部。南部和北部网格单元的位移时间序列如图6(c)所示，负值表示北部的网格单元向南移动，正值表示南部的网格单元向北移动，两者均向水库的质心移动。对于5 a、10 a和15 a蓄水策略，北向位移的年平均位移量分别为4.4 mm、2.2 mm和1.5 mm，南向位移的年平均位移量分别为2.6 mm、1.3 mm和0.8 mm。

表1为不同蓄水策略下的年位移变化、位移总变化和最大位移变化。可以看出，蓄水的速度越快，年变形量越大。总体而言，在水库蓄水完成后(注满74 km3)，存储层将产生约59 mm的垂直位移、22.5 mm的北向位移、13 mm的南向位移、9.2 mm的东向位移和6.7 mm的西向位移。

表1 不同蓄水策略下的年位移变化、总位移变化和最大位移变化

3 结 语

本文提出了一种基于球谐变换预测GERD水库地表位移分量的方法。分别假定5 a、10 a、15 a蓄满水库，则由此引发的地表垂直形变速率分别约为11.8 mm/a、5.9 mm/a、3.9 mm/a；引发的南向和北向位移速率分别约为2.6 mm/a和4.4 mm/a、1.3 mm/a和2.2 mm/a、0.8 mm/a和1.5 mm/a；引发的东向和西向位移速率分别约为1.8 mm/a和1.4 mm/a、0.9 mm/a和0.7 mm/a、0.6 mm/a和0.4 mm/a。同时实验发现，蓄水速度越快，月/年形变量越大。

其次，通过60阶、700阶、1 500阶和2 300阶的球谐展开对比发现，高阶次球谐波的截断会导致边缘信息丢失和空间信息的平滑和扩展。为了减少该效应对本文结果的影响，经过对比，最后选定2 300阶的截断来完成实验。对能量守恒定理的分析和输入的平均水高与所求EWH仅1.6%的误差率均证明了本实验的合理性。