腐蚀管道极限弯矩计算的理论和方法
2021-12-01李思源李逸轩
李思源,李逸轩
(1.兰州石油机械研究所,兰州 730050;2.兰州理工大学 工程技术学院,兰州 730300)
0 引言
近半个世纪以来,国内外对管道剩余强度的评估开展了许多研究工作,其中BOUWKAMP等[1-2]对无缺陷管道在联合载荷下极限承载力进行了大量的数值分析和试验研究。基于塑性失效理论,采用理想弹塑性本构模型,MOHAREB等[3-8]提出了无缺陷管道在内压、轴向力和弯矩联合载荷下的极限承载力解析解,并与试验结果进行比较,得出该简化方法能很好地预测管道极限承载力;其后,BAI等[9-12]将这部分工作扩展到了腐蚀管道,将管道腐蚀形状简化为减薄深度在环向不发生变化,分别针对4种不同工况的等深减薄管道,提出了极限弯矩计算方法。该方法被ABS[13]采用,评估腐蚀海底管道剩余强度。文献[14-15]采用Hill屈服准则,推导了不规则腐蚀缺陷管道在内压、轴向力和弯矩联合作用下极限承载力广义计算公式。文献[16]证明了文献[9-15]中极限弯矩计算式的理论依据不充分,并对承受内压p、轴向力F和弯矩联合作用下的局部减薄管道建立了极限弯矩计算的新公式。文献[9-15]对腐蚀管道在内压、轴向力和弯矩联合作用下推导的极限弯矩计算式只有在纯弯曲载荷下才成立;当内压p>0时,文献[9-12]中定义的环向应力在管道未减薄区不一定满足屈服准则,文献[14-15]采用的环向应力σθ=pRm/t在管道腐蚀区不一定满足屈服准则。实例计算结果表明[16]:当内压p>0时,文献[9]中极限弯矩计算式的计算值都比文献[16]中新公式的计算值小;文献[14-15]中极限弯矩计算式的计算值都比文献[16]中新公式的计算值大。因此,文献[9-15]尚未解决腐蚀管道在内压、轴向力和弯矩联合作用下极限承载力的计算问题。文献[16]也是将管道腐蚀形状简化为减薄深度在环向不发生变化的情况下得到的,这种简化模型一般会使极限弯矩的计算结果偏于保守。因此,进一步研究腐蚀管道极限承载力的计算方法很重要。
本文对承受内压p、轴向力F和弯矩联合作用的多级等深减薄管道,应用屈服准则,推导出管道横截面弯曲压缩侧和弯曲拉伸侧应力极限值的计算式;采用理想弹塑性本构模型,建立了多级等深减薄管道在联合载荷作用下的极限弯矩计算理论和计算公式;提出腐蚀管道在联合载荷作用下极限弯矩的工程计算方法。
1 基本理论
1.1 基本假定和简化
(1)管道钢材不考虑应变强化作用,采用理想弹塑性应力-应变本构关系;
(2)管道在达到全塑性状态前,管道的横截面形状不发生改变;
(3)在管道达到极限状态时,塑性中性轴将管道横截面分为弯曲压缩和弯曲拉伸两个区域,管道截面达到相应的全塑性状态。
1.2 局部减薄管道的屈服准则
设管道的外半径为Ro,管壁厚度为t,平均半径Rm=Ro-t/2;设管道内壁存在深度为dj,环向截面夹角为βj(j=1,2,…,n)的n级对称等深减薄缺陷(见图1),其轴向长度很长。且:
dk=max{d1,…,dn}
(1)
dh=min{d1,…,dn}
(2)
(3)

图1 n级对称等深减薄管道横截面几何尺寸和塑性中性轴示意Fig.1 Schematic diagram of the geometric dimensions andplastic neutral axis of the cross section of the n-level symmetricalequal-depth thinned pipe
对于各向异性材料的管道,在内压p、轴向力F和弯矩M联合作用下发生屈服时,采用屈服准则可以得到:
(4)
式中,σz为管道轴向应力;σzl为管材轴向屈服应力;α为各向异性系数,一般可取α=σθl/2σzl;σθ为管道环向应力;σθl为管材环向屈服应力。
求解式(4)得到轴向应力σz的解:
(5)
(6)
1.3 管道弯曲屈服的轴向极限应力
含n级等深减薄管道(见图1)在内压p、轴向力F和弯矩联合作用下,管道的环向应力σθ由内压p产生;内压p对该管道产生的轴向力Fp作为轴向力F的组成部分。管道的轴向应力σz只由轴向力F和弯矩产生。
在管道减薄深度为dj(j=1,2,…,n)的部位,管道的环向应力σθj由内压p产生,且近似为:
σθj=p(Rm+0.5dj)/(t-dj) (j=1,2,…,n)
(7)
(1)当管道减薄深度为dj的部位(见图1)处于弯曲压缩侧时,将式(7)代入式(6)得到,该部位屈服的轴向应力极限值σcj用式(8)计算。
(j=1,2,…,n) (8)
(2)当管道减薄深度为dj的部位(见图1)处于弯曲拉伸侧时,将式(7)代入式(5)得到,该部位屈服的轴向应力极限值σtj用式(9)计算。
(j=1,2,…,n) (9)
1.4 极限应力不等式
(1)第一极限应力不等式。
当管道的内压p>0,管道等深减薄深度di和dj有di>dj时,则屈服的轴向极限应力σci和σcj满足不等式:
σci>σcj
(10)
由式(7),并计及di>dj得到:
σθi-σθj>0
(11)

计及式(11),则有vj-vi>0。因此有:
(12)
将式(8)代入计算式(σci-σcj)/σzl,并利用式(11)(12)得到:
(13)
由此得到不等式(10)成立。
由第一极限应力不等式可直接推出第二极限应力不等式。
(2)第二极限应力不等式。
当管道的内压p>0,管道等深减薄深度dj>0(j=1,2,…,n,j≠h)时,则屈服的轴向极限应力σcj和σch满足不等式:
σcj>σch(j=1,2,…,n,j≠h)
(14)
2 多级等深减薄管道极限弯矩计算理论
2.1 多级等深减薄管道承载弯矩载荷的条件
含n级对称等深减薄管道(见图1)横截面的面积S用下式计算:

(15)
管道在内压p和轴向力F联合作用下,管道的轴向应力σz(F)近似为:
σz(F)=F/S
(16)
令:
Fl=Sσzl
(17)
(1)承载弯矩载荷的条件。
含n级对称等深减薄管道(见图1)在内压p和轴向力F联合作用下,用式(7)计算管道最大减薄为dk部位的环向应力σθk和最小减薄为dh部位的环向应力σθh,用式(17)计算Fl。该管道能承载弯矩载荷的条件为:
(18)
且
(19)
(20)
(2)在承载弯矩载荷的条件下。
σch<σcj<σz(F) (j=1,2,…,n)
(21)
σtj>σz(F) (j=1,2,…,n)
(22)
验证如下。
(1)含n级对称等深减薄管道(见图1)在内压p和轴向力F联合作用下,管道产生的轴向应力σz可用式(16)近似计算,再应用式(17)得到:
利用上式和式(7)计算的环向应力σθj得到,在管道减薄深度为dj(j=1,2,…,n)的部位都有:
(j=1,2,…,n) (23)
①由式(1)得到dj≤dk,因此由式(7)计算得到σθj≤σθk。
σθj/σθl≤σθk/σθl(j=1,2,…,n)
又利用式(19)得到:
(j=1,2,…,n)
由上式推出:
(24)
②由式(2)得到dj≥dh,因此由式(7)计算得到σθj≥σθh。
σθj/σθl≥σθh/σθl(j=1,2,…,n)
再利用式(20)得到:
(j=1,2,…,n)
由上式推出:
将式(24)和上式代入式(23)得到,在n级等深减薄管道的各等深减薄部位都有:
因此,含n级对称等深减薄管道(见图1)在内压p和轴向力F联合作用下没有屈服,该管道还可以承载一定的弯矩载荷。
(3)在承载弯矩载荷的条件下,含n级对称等深减薄管道由内压p产生的环向应力σθj和轴向力F都满足不等式(24) 。
采用反证法证明式(21)和式(22)都成立。
2.2 多级等深减薄管道极限弯矩的计算公式
根据承载弯矩的条件,计算n级对称等深减薄管道在内压p、轴向力F和弯矩联合作用下的极限弯矩时,内压p产生的环向应力σθk,σθh和轴向力F必须同时满足不等式(18)~(20)。
当管道在弯矩作用下达到全塑性状态时,设塑性中性轴的夹角为ψ。考虑塑性中性轴的位置,可按两种工况计算管道的极限弯矩:工况1——塑性中性轴下方的管壁区域位于弯曲压缩侧,塑性中性轴上方的管壁区域位于弯曲拉伸侧;工况2——塑性中性轴下方的管壁区域位于弯曲拉伸侧,塑性中性轴上方的管壁区域位于弯曲压缩侧。
(1)工况1的极限弯矩计算公式。
在工况1条件下,当塑性中性轴位于面积为As(s∈{1,2,…,n})区域中时,则面积为A1,…,As-1的区域都在弯曲压缩侧,面积为As+1,…,An的区域都在弯曲拉伸侧。当管道在弯矩作用下达到全塑性状态时,管道的轴向力F可近似表示为:
(25)
式中,σcj用式(8)计算;σtj用式(9)计算;Aj分别为图1中对应区域的面积,且:
k1j=(1-dj/t)[1+dj/(2Rm)] (j=1,2,…,n)
Aj=2k1jβjRmt(j=1,2,…,n)
将上面诸式代入式(25),得到塑性中性轴夹角的一次方程式,当s∈{1,2,…,n}时,塑性中性轴的夹角ψ=ψs用式(26)计算。

且0<ψ1<β1。
当s∈{2,…,n-1}时:

(26)

当s=n时:
且π-βn<ψn<π。
设:
k2j=(1-dj/t)[1+dj/(2Rm)]2(j=1,2,…,n)
(j=1,2,…,s-1)
(j=s+1,2,…,n)
当塑性中性轴位置用式(26)筛选确定为ψ=ψs后,n级对称等深减薄管道极限弯矩M(p,F)为:

(27)
将诸参量代入式(27)得到式(28)~(30)。
当s=1时:

(28)
当s∈{2,…,n-1}时:

(29)
当s=n时:

+[sinψn-sin(π-βn)]k2nσcn-sinψnk2nσtn
(30)
(2)工况2的极限弯矩计算公式。
在工况2的条件下,当塑性中性轴位于面积为As的区域中时,则面积为A1,…,As-1的区域都在弯曲拉伸侧;面积为As+1,…,An的区域都在弯曲压缩侧。当管道在弯矩作用下达到全塑性状态时,轴向力F可近似表示为:
式中,σtj用式(9)计算,σcj用式(8)计算;Aj为图1中对应区域的面积。
类似于上面工况1的方法可以得到工况2的极限弯矩计算公式。
3 腐蚀管道极限弯矩的计算方法
许多压力管道,由于输送介质的腐蚀性和重力作用,在管道横截面内壁6点钟位置两侧产生腐蚀缺陷,腐蚀形状沿腐蚀区中心线(6点钟处)近似于对称分布(见图2),且缺陷的轴向长度很长。

图2 腐蚀管道横截面尺寸示意Fig.2 Schematic diagram of the corroded pipe cross section
以下采用简便的方法将图2中的腐蚀管道简化为n级对称等深减簿管道,然后采用以上多级等深减薄管道极限弯矩计算理论和公式,即可导出腐蚀管道极限弯矩的工程计算方法如下。
(1)已知参数。
①管道的平均半径Rm,壁厚t,管材轴向屈服应力σzl,环向屈服应力σθl;
②管道内壁腐蚀缺陷的环向夹角为2β(见图2),轴向腐蚀长度很长;
③管道承受内压p和轴向力F。
(2)构建n级对称等深减薄管道。
在腐蚀管道的横截面上(见图2),给定n(n∈{6,8,10}),用通过圆心O的n+1条线段O0,O1,…,On将β角分成n等份,各等份的角度为β/n。又沿线段O0,O1,…,On测量得到管壁对应的腐蚀深度分别为a0,a1,…,an-1,an=0;取d1=(a0+a1)/2,…,dj=(aj-1+aj)/2,…,dn=an-1/2,将图2中的腐蚀管道简化为图3中减薄深度为dj、夹角为β/n的n级等深减薄管道。

图3 腐蚀管道简化为 n级对称等深减薄管道横截面尺寸和塑性中性轴示意Fig.3 Schematic diagram of the geometric dimensions andplastic neutral axis of the cross section of the n-level symmetricalequal-depth thinned pipe which is simplified from the corroded pipe
(3)计算腐蚀管道的极限弯矩。
① 计算参量:
d=max{a0,a1,…,an-1,d1,…,dn}
σθj=p(Rm+0.5dj)/(t-dj) (j=1,2,…,n)
σθd=p(Rm+0.5d)/(t-d)(σθ0=pRm/t)
k1j=(1-dj/t)[1+dj/(2Rm)] (j=1,2,…,n)
k2j=(1-dj/t)[1+dj/(2Rm)]2(j=1,2,…,n)
②验证不等式成立。

且:
③计算管道弯曲屈服的轴向极限应力σcj,σc,σtj,σt。
(j=1,2,…,n)
(j=1,2,…,n)
④计算腐蚀区全部或者部分在弯曲压缩侧的极限弯矩。
a.计算:
当ψn+1>β时,确定塑性中性轴的ψ=ψn+1,管道的极限弯矩用下式计算:

+(sinψn+1-sinβ)σc-sin(ψn+1)σt}
b.当ψn+1<β时,计算:

+n(π/β-1)σt]β/n}÷[2Rmtk1s(σcs-σts)]
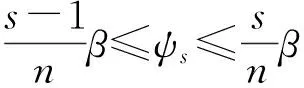

⑤计算腐蚀区全部或者部分在弯曲拉伸侧的极限弯矩。
a.计算:
当ψn+1>β时,确定塑性中性轴的ψ=ψn+1,管道的极限弯矩用下式计算:

+(sinψn+1-sinβ)σt-sin(ψn+1)σc}
b.当ψn+1<β时,计算:

+n(π/β-1)σc]β/n}÷[2Rmtk1s(σts-σcs)]
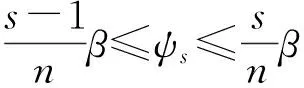

4 腐蚀管道极限弯矩算例
4.1 纯弯曲载荷下的算例
文献[15]研究了腐蚀缺陷管道的极限承载力;文献[16]指出,在内压、轴向力和弯矩联合作用下,文献[15]中的极限弯矩计算公式的理论依据是不充分的,但在纯弯曲下仍然成立。因此文献[15]采用数值方法计算的等深腐蚀、椭圆腐蚀和抛物线腐蚀管道在纯弯曲下的极限弯矩值是有效的。
现以文献[15]表1中工况3试件TP3为例,采用腐蚀管道极限弯矩的工程计算方法,计算工况3试件TP3的极限弯矩值,并和数值解极限弯矩值进行比较,验证工程计算方法的计算精度。
TP3试件管的平均半径Rm=52.85 mm,管壁t=8.6 mm,管材钢轴向屈服应力σzl和环向屈服应力σθl为:σzl=σθl=408 MPa,各向异性系数α=0.5;管子横截面腐蚀区中心线位置的最大深度a0=6.9 mm,腐蚀夹角2β=π;腐蚀深度函数a(θ)计算如下。
半椭圆腐蚀:
(31)
抛物线腐蚀:
a(θ)=6.9(1-2θ/π)2(0≤θ≤π/2)
(32)
(1)取n=6,用射线O0,O1,…,O6将管子横截面腐蚀区分成6等份,各等份的角度为π/12 (或15°)。计算射线Oj对应的腐蚀角度θj和腐蚀深度aj=a(θj) (j=0,1,…,6)。
(2)取dj=(aj-1+aj)/2计算6级等深减薄深度d1,…,d6。构建6级对称等深减薄dj,βj=π/12计算模型(见图3)。
(3)半椭圆腐蚀试件TP3极限弯矩计算结果。
在纯弯曲下,p=0,F=0,因此,由第3节工程计算方法中(3)③计算得到弯曲屈服的轴向极限应力:
σcj=σc=-σzl=-408 MPa
σtj=σt=σzl=408 MPa
利用半椭圆腐蚀管道6级等深减薄模型数据d1,…,d6,计算k1j和k2j;在弯曲拉伸侧,由第3节工程计算方法中(3)⑤a.的ψ7计得ψ7=0.649 5π>β。因此塑性中轴的ψ=ψ7=0.649 5π,半椭圆腐蚀试件TP3的极限弯矩Me(0,0)=21.76 kN·m。
(4)抛物线腐蚀试件TP3的极限弯矩Mp(0,0)=31.56 kN·m。
(5)从文献[15]表2中查得:半椭圆腐蚀工况3试件TP3极限弯矩的数值解Mecpc=21.4 kN·m,抛物线腐蚀试件TP3极限弯矩的数值解Mpcpc=31.7 kN·m。由此得到:半椭圆腐蚀的Me(0,0)和Mecpc=21.4 kN·m的误差为 -1.68%,抛物线腐蚀的Mp(0,0)和Mpcpc=31.7 kN·m的误差为 0.44%。
4.2 联合载荷下的算例
设管道的平均半径Rm=500 mm,管壁t=20 mm,管材钢轴向屈服应力σzl和环向屈服应力σθl为:σzl=σθl=500 MPa,各向异性系数α=0.5;管子横截面腐蚀区中心线位置的最大深度a0=10 mm,腐蚀夹角2β=π;腐蚀深度函数a(θ)计算如下。
半椭圆腐蚀:
(33)
抛物线腐蚀:
a(θ)=10(1-2θ/π)2(0≤θ≤π/2)
(34)
管道承受内压p=10 MPa,轴向力F=20 000 kN。
(1)对半椭圆腐蚀管道和抛物线腐蚀管道,取n=6,用射线O0,O1,…,O6将管道横截面腐蚀区分成6等份,各等份的角度为π/12(15°)。计算射线Oj对应的腐蚀角度θj和深度aj=a(θj) (j=0,1,…,6) 。
(2)取dj=(aj-1+aj)/2,计算半椭圆腐蚀管道6级等深减薄深度d1,…,d6。构建6级等深减薄dj,βj=π/12计算模型(见图3)。利用椭圆腐蚀管道6级对称等深减薄模型数据d1,…,d6,计算k1j和k2j;计算管道弯曲屈服的轴向极限应力σcj,σc,σtj,σt。
(3)验证半椭圆腐蚀管道在内压p=10 MPa和轴向力F=20 000 kN联合作用下,满足承载弯矩载荷的条件。
(4)在弯曲压缩侧,由第3节工程计算方法中(3)④a,取s=5,计算ψ5=0.396 1π,因此塑性中性轴的ψ=ψ5=0.396 1π,半椭圆腐蚀管道的极限弯矩为:
Me(10,20 000)=5 855.8 kN·m
采用和上面相同的方法,得到含抛物线腐蚀(见式(34))管道的极限弯矩为:
Mp(10,20 000)=6 515.3 kN·m
5 结语
(1)对在内压p、轴向力F和弯矩联合作用下的n级对称等深减薄管道,建立了承载弯矩载荷的条件,应用很简便。
(2)对n级对称等深减薄管道在内压p、轴向力F和弯矩联合作用下,应用屈服准则和理想弹塑性本构模型,分两种工况建立了该管道极限弯矩的计算理论和计算公式。
(3)对承受内压p、轴向力F和弯矩联合作用的腐蚀管道,建立了管道极限弯矩的工程计算方法。
