基于卡尔曼滤波的大跨度斜拉桥变形预测研究

张 豪，张利莎

(浙江工业大学 土木工程学院，浙江 杭州 310023)

桥梁是交通运输的重要组成部分，是交通行业的关键节点。大型桥梁结构的复杂性引起了人们对桥梁运营安全性的重视。国外斜拉桥检测的研究主要集中于结构的新型检测方法，Ho等[1]介绍了基于图像检测的新型结构损伤检测理论，在实际工程中可以适用3 种索；Zonta等[2]通过将基于贝叶斯数据融合到传感器系统应用到实际工程中，研究表明该钢混叠合梁斜拉桥因索力松弛导致实际与设计出现较大偏差，需要对结构进行承载力评估。常用的预测分析方法有多种，如多元线性回归理论、灰色系统分析理论和神经网络分析理论等，但在实际工程中，引起结构变形的因素较复杂，难以用固定的模态表示出自变量与因变量之间的关系，且通用性较差。笔者采用的卡尔曼滤波预测理论具有强大精准的预测功能和通用性，被广泛应用在桥梁、大坝、基坑和地铁等土木领域的数据研究中。

卡尔曼滤波模型是一种动态的数据分析模型，利用一组状态方程和观测方程描述观测体系，并在观测过程中不断修正、迭代其预测值。奕瑞明[3]提出将Kalman滤波方法应用到形变监测数据处理中，导出多种形式的形变监测网的状态方程和观测方程；张福荣[4]较为系统地阐述了Kalman滤波的基本原理，并重点讨论和研究了利用方差补偿自适应Kalman滤波理论建立的监测数据处理理论、方法和模型；陈小杰等[5]通过建立卡尔曼滤波模型，对上海某历史建筑在基础托换期间的沉降监测数据进行滤波和预测，同时基于卡尔曼滤波数据进行多项式回归预测，与传统的多项式回归分析模型进行预测对比分析，取得了较好的结果。笔者将卡尔曼滤波理论运用到预测大跨度斜拉桥的结构变形的问题中，利用相近位置监测点应变和挠度的设计值与实测值的偏差，预测下一位置应变和挠度，为桥的工程设计、施工、健康监测提供理论依据和技术支撑。

1 基于卡尔曼滤波理论的结构变形预测模型

变形现象普通存在于自然界中，在土木工程领域，当建筑物或构筑物的变形量超过其本身所能承受的极限值时，便会发生安全事故。大型桥梁的变形特征可分为长期形变和短期形变两种情况。长期形变是指由索力松弛、桥体断裂等引起的长久性形变；短期形变是指由风、地震、桥面交通运输荷载变化引起的短暂性形变。长期变形不可恢复，但随着外力的减小，短期变形可恢复或基本恢复至原始状态[6]。

笔者以浙江省某大跨度叠合梁斜拉桥为监测对象，利用卡尔曼滤波预测模型对其初始应变和挠度的监测数据进行处理、分析，以研究该桥的变形情况。卡尔曼滤波理论是最初由R.E.Kalman在1960年提出的一种线性递推优化方法，算法本质是从被噪声污染的信号中提取真实的部分，进而估计出系统的真实状态。笔者将变形监测点数据作为观测序列输入到一个随机系统，利用直观的监测方法，推导出白噪声作用下非稳定系统的卡尔曼滤波预测方程。基于卡尔曼滤波理论的预测分析无需现场记录诸多系统过去的状态值，只需掌握前一个状态预测结果的误差协方差矩阵即可，故可适用于实时动态系统[7]。

1.1 线性随机系统的离散化模型

取观测点的状态向量为

(1)

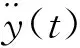
(2)

其解为

(3)

故线性随机系统的离散时间模型可表示为

yk=μk-1yk-1+Gk-1ωk-1

(4)

zk=Ekyk+rk

(5)

式中：yk为系统状态向量；zk为观测向量；ωk为系统噪音；rk为观测噪音；μk-1为状态转移矩阵；Ek为观测矩阵；Gk-1为系统噪音的系数矩阵。

1.2 基于卡尔曼滤波理论的结构变形预测模型

初始的卡尔曼滤波方程是最优估计问题的唯一实际的有限维解决方法，可对无法控制的动态系统可能出现的未来行为进行预测，如桥梁应变、挠度等。首先，利用该系统的过程模型预测系统下一个状态[8]。设yk为第k个监测点的设计值，φk是线性转换系数，其计算公式为

(6)

由于在实际工程中，结构变形监测点的实测值与设计值是不一致的，测量误差是客观存在的，因此该预测模型引入线性转换系数，线性转换系数可解决卡尔曼滤波预测模型误差较大的难题。设当前系统状态是k，P表示其协方差，该系统的模型可利用系统的前一状态预测当前系统状态，该系统的状态方程为

(7)

(8)

以已知的当前监测点的预测结果为基础，结合当前监测点的实测值，可得到当前状态k的最优化估算值为

(9)

(10)

(11)

2 工程实例

2.1 工程概况

浙江省某座特大桥的约束采用半漂浮体系，其主梁为钢结构，桥面为混凝土结构。桥梁中心桩号K149+442，桥梁全长948 m。桥梁结构形式为(85+145+488+145+85)m双塔整幅叠合梁斜拉桥[9]，边中跨比0.471，边跨设辅助墩，桥梁位于半径R=25 000 m、切线长T=587.5 m、外矢距E=6.903 m的圆弧竖曲线上；横向布置为2.75 m(风嘴及索道)+0.50 m(防撞护栏)+15.25 m(车行道)+1.50 m(中央护栏)+15.25 m(车行道)+0.50 m(防撞护栏)+2.75 m(风嘴及索道)。钢梁主体结构采用Q345D低合金钢，混凝土预制桥面板采用C55海工耐久混凝土，接缝采用C55微膨胀混凝土，箱梁压重混凝土采用铁砂混凝土，容重不小于38.0 kN/m3。该桥桥型的布置如图1所示。

图1 该桥主通航孔桥桥型布置图(单位：cm)

2.2 试验测试截面的确定

对于大跨度斜拉桥，应重点观测主跨、主梁、主塔、辅助墩、变跨主梁、斜拉索等结构受力以及其他变形敏感部位。笔者依据该桥的实际工程情况并结合桥梁荷载试验的相关规范要求，选取边跨主梁最大正弯矩、挠度(Ⅰ-Ⅰ截面)、Z2#辅助墩墩顶主梁最大负弯矩(Ⅱ-Ⅱ截面)、次边跨主梁最大正弯矩、挠度(Ⅲ-Ⅲ截面)、中跨Z3#墩附近主梁负弯矩(Ⅳ-Ⅳ)截面、中跨l/2跨主梁最大正弯矩/主梁跨中最大挠度(Ⅴ-Ⅴ)、主塔最不利弯矩(Ⅵ-Ⅵ)、主塔顶部最大偏位(VII-VII)、Z1#墩顶主梁纵桥向变位(VIII-VIII)、活载下最大索拉力等共9 个测试位置[10-11]。测试截面和测试内容如表1所示。

表1 静载试验测试截面及测试位置

2.3 试验测试截面监测点的确定

该桥结构设置应变和挠度的监测点较多。因篇幅受限，故只详细介绍主梁的应变和挠度监测点。

2.3.1 主梁应变监测点

因I-I，II-II截面箱内底板存在压重块，故无法布置箱内底板应变片。将I-I，II-II截面测点均布置于箱室外，每个截面布置17 个应变测点，如图2所示。

图2 桥梁Ⅰ-Ⅰ，Ⅱ-Ⅱ测试截面应变监测点布置示意图(单位：cm)

2.3.2 主梁挠度监测点

该桥主梁桥面纵向挠度采用两台Leica TCA2003智能全站仪进行测试，测站分别架设于两侧主墩承台上，测点采用棱镜固定于钢箱梁底板两侧。全桥主梁左右侧各布置15 个(共30 个)挠度测点，纵桥向分别位于边跨2等分点、次边跨4等分点、主跨8等分点处[12]，如图3所示。

图3 桥梁挠度监测点布置示意图(单位：cm)

3 卡尔曼滤波预测模型在桥梁变形中的应用

卡尔曼滤波主要通过反复迭代计算实现，即通过了解某一特定时刻的观测值和前一期的最优估计值，然后利用该系统的状态方程采用递推的方式获取新一期的估计值。尤其适用针对大型桥梁结构的变形研究，即通过对监测对象的变形量不断的观测及预测，估计出该系统的实际状态，进而达到对桥梁结构的每一工况进行实时控制的目的。卡尔曼滤波预测的难点是如何精准地确定系统的初始状态，当观测数据量有限时，倘若初始值的选取不准确，就容易使得所测结果收敛较慢甚至发散且误差较大，进而导致部分信息被隐藏，难以达到滤波的最佳效果。

研究表明：初始状态向量可通过前两期观测结果确定，可取第二期平差后的测点位置作为新的初始位置，根据监测网等级和变形监测的精确度要求确定初始值的方差值，观测噪声的方差矩阵通常根据观测仪器的精度和测量方法确定[13-14]。本次试验通过分别监测该桥的应变变形和挠度变形，确定该桥的变形状况，为评价该桥的结构健康及安全状况提供基础资料。因该工程所布设的监测点较多，监测数据较多，故以图2中I-I截面的11号混凝土应变监测点和图3中左侧L8挠度监测点为例进行分析。

3.1 I-I截面11号位置应变的预测

选取图2中I-I截面7，8，9，10号应变设计值和实测值，其基本数据如表2所示。

表2 应变预测基本数据准备表

选取11号混凝土应变为观测向量，状态向量为10号混凝土应变，初始值的实测值为2 με，则该系统的观测数据向量为

Z9=(-2，-5，-8，2)

观测函数为e(2,11)=(-18，-22，-26，-22)，可知其观测矩阵为

(-3，-5，-9，-7)

依据式(3～11)，可得出该监测点应变的卡尔曼估计结果，如表3所示。11号监测点应变的预测数据首次迭代后的预测值为-0.637 με，与迭代多次后的结果0.969 με相差较大。说明卡尔曼滤波法去噪不是一次迭代完成的，需要进行多次迭代，使预测值逐渐逼近去噪后的数值。在第3 次时迭代应变预测差值最大，为1.238 με，之后便从第4 次开始收敛。11号点的应变值最终预测结果为0.969 με，与实测值相差0.031 με。

3.2 左侧L8位置挠度的预测

左侧L8位置挠度预测基本数据准备表如表4所示。

表4 挠度预测基本数据准备表

选取L8号挠度为观测向量，状态向量为L7号挠度，初始值取-7.58 mm，则该系统的观测数据向量为

Z9=(3.52，1.71，-2.49，-5.17，-7.58)

Y8=-7.58

观测函数为e(-7.58,8)=(6.96，3.67，-5.14，-10.21，-13.63)，可知其观测矩阵为

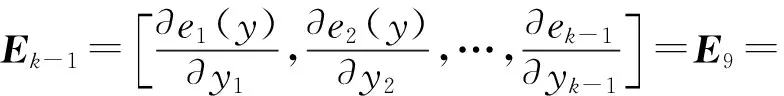
(3.11，1.35，-2.64，-6.58，-9.34)

取观测噪音的方差为2，系统噪音ω为0.1，取初始值Y0的方差为2，根据式(3～11)可得出图3中左侧L8监测点挠度预测值，如表5所示。从表5数可知，L8监测点的挠度值经首次迭代的预测值为-5.107 mm，反复迭代后预测值为-6.434 mm，与实测值相差0.044 mm。

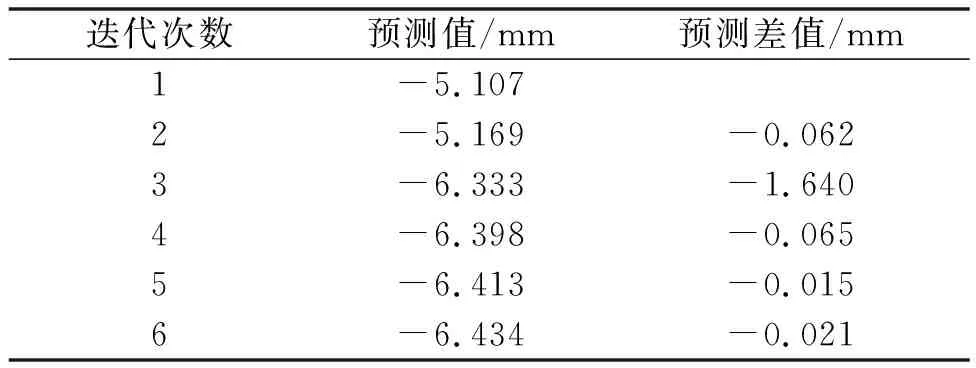
表5 挠度变形预测结果表

同理可得该桥主梁I-I截面17 个应变监测点和主梁左侧15 个挠度监测点的滤波曲线，如图4～5所示。为便于分析，将该桥主梁I-I截面中布设的各个应变监测点和主梁左侧挠度的监测点分别自然排序、编号。从图4可知：主梁I-I截面中17 个应变监测点预测值与实测值的差值最大的点为第7 个监测点和第17 个监测点，分别约为1.94，2.32 με，可见卡尔曼滤波理论用于大跨度斜拉桥的结构变形预测的理论值与实测值较为接近，在实际工程预测问题中具有良好的精准度。由图5可知：主梁左侧挠度监测点预测值与实测值差值最大的点为L3，L10，分别约为1.72，1.79 mm。测点布设的数量对预测结果的收敛速度和精准度有很大影响，一般而言，测点越多收敛速度越快，收敛精度也越高。

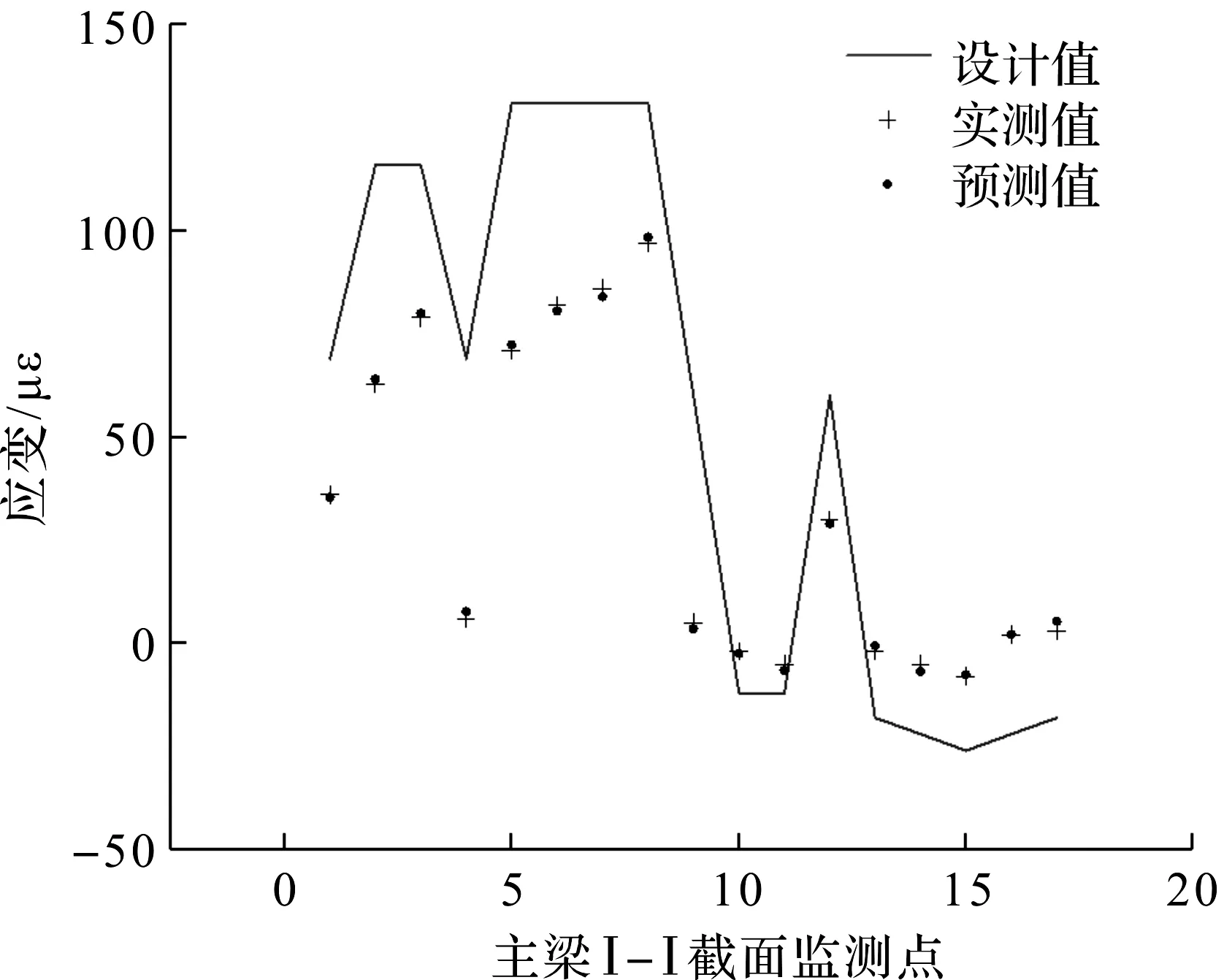
图4 卡尔曼滤波应变结果

图5 卡尔曼滤波挠度结果

实际工程应用时受到较多因素影响，与理论之间存在偏差，因此通常需参照荷载最大值进行桥的设计。采用卡尔曼滤波理论预测大型桥梁的变形情况为桥梁的前期设计提供有力的依据，可以提高材料的利用率，亦为桥梁后续的健康监测提供科学有效的技术支撑[15]。

4 结 论

大型斜拉桥在国家交通的正常运行中起着不可或缺的作用，它们影响着国民生活、生产的各个方面。至2020年底，我国新建的大、中、小各式桥梁约20余万座。在桥梁的设计、施工和运营管理中存在的不足会导致桥梁的实际寿命达不到其设计使用期限。笔者将卡尔曼预测模型运用到大跨度叠合梁斜拉桥的结构变形预测中，通过掌握该桥主梁中具有代表性的17 个应变监测点和15 个挠度监测点的原始数据，预测所选截面下一状态的应变变形与挠度变形情况并与其实测值进行对比。研究表明：卡尔曼滤波预测模型可以精准地预测大跨度叠合梁斜拉桥的结构变形情况，为此类桥梁结构的运营工作及长期的健康监测提供科学可靠的理论依据。