变截面波形钢腹板弹性整体屈曲计算及几何参数分析

冀伟，马建红

（兰州交通大学 土木工程学院，甘肃 兰州 730070）

波形钢腹板-混凝土组合箱梁采用波形钢腹板代替了混凝土箱梁的混凝土腹板，不仅减轻了桥梁上部结构的重量，而且改善了混凝土腹板易开裂的通病，提高了桥梁的跨越能力[1-2].对于大跨度的变截面波形钢腹板-混凝土组合箱梁，波形钢腹板的抗剪性能成为制约桥梁跨越能力的主要因素.因此，研究变截面波形钢腹板的剪切屈曲性能对波形钢腹板的抗剪设计有重要意义.

国内外学者已对波形钢腹板的剪切屈曲性能进行了大量研究，Yi 等[3]基于小变形理论将单位长度的矩形波形钢腹板简化为正交异性板，提出了单位长度的矩形波形钢腹板的剪切屈曲荷载计算方法.Dou等[4]以具有加劲肋的平钢腹板剪切屈曲的理论为基础，得到了波形钢腹板剪切屈曲强度的计算公式.Easley 和Mcfarland[5]基于能量变分法和小挠度理论，引入屈曲位移形函数，提出了波形钢腹板的弹性整体屈曲荷载计算公式.随后，Easley 在已有波形钢腹板整体剪切屈曲强度理论的基础上，提出了Ealsey公式.Abbas 等[6]对波形钢腹板工字梁的抗剪性能进行了研究，提出了波形钢腹板屈曲强度和抗剪强度的计算公式.近年来，Hassanein 等[7]、Leblouba 等[8]、Lee 等[9]、Zevallos 等[10]和Padmanaban 等[11]利用数值模拟和试验研究的方法对波形钢腹板剪切屈曲模式及抗剪性能展开研究，分析了不同几何参数对波形钢腹板抗剪性能的影响.宋建永等[12]对不同因素影响下的波形钢腹板的剪切屈曲极限荷载和屈曲模态进行了研究分析.周绪红等[13]利用有限元法分析了不同几何参数对波形钢腹板剪切屈曲的影响，提出了计算波形钢腹板屈曲强度的理论公式.聂建国等[14]推导了弹性扭转约束边界下波形钢腹板的剪切屈曲强度的计算公式，给出了4 种简化边界条件下的波形钢腹板的剪切屈曲强度计算公式；并通过试验和数值模拟相结合的方法研究了室内试验梁的抗剪性能，对波形钢腹板屈曲强度和抗剪强度进行了研究[15-16].李立峰等[17]研究了室内波形钢腹板H 型梁的基本破坏形态，通过试验值与有限元值对比，分析了波形钢腹板弹性屈曲强度和非弹性屈曲强度的计算公式.

目前，已有研究成果大多基于小跨度等截面波形钢腹板组合箱梁或H 型室内试验梁，对变截面波形钢腹板的研究相对较少，并且在研究波形钢腹板几何参数对其剪切屈曲敏感性影响时，大多采用随机波长.此外，现有对波形钢腹板弹性整体剪切屈曲强度的计算公式，如Bergmann-Reissner 公式、Ealsey公式、Hlavacek 公式及Abbas 公式等，在计算波形钢腹板的屈曲强度时，认为剪切屈曲系数仅与波形钢腹板的边界条件有关，忽略了波形钢腹板长度的影响，这对长度较大的波形钢腹板的剪切屈曲强度计算不够准确.本文在计算波形钢腹板整体屈曲长度时，将相邻横隔板之间的波形钢腹板简化为顺桥向（x 方向）和竖桥向（y 方向）具有不同抗弯刚度的正交异性板，边界条件按四边简支条件考虑，运用伽辽金法和变分原理，推导了变截面波形钢腹板弹性整体屈曲强度的计算公式，并运用有限元软件对变截面波形钢腹板弹性剪切屈曲强度敏感性进行了分析研究.

1 板的平衡微分方程

1.1 小挠度理论的基本假定

基于小挠度理论建立薄板的平衡微分方程时，引入以下基本假定：

1）板发生屈曲时z 方向正应力和剪应力为0，且板厚度方向任意位置的挠度近似等于板中面的挠度.

2）薄板的竖向位移远小于其厚度尺寸，忽略薄板中面因弯曲变形而产生的薄膜力.

3）薄板在弹性范围内发生弯曲变形.

建立变截面波形钢腹板的平衡微分方程时，将波形钢腹板简化为正交异性板，其微元体中面变形和内力图如图1 所示.

图1 中，Fx、Fy和Fxy为板的中面力，ω 为板微元体的挠度，Qsx、Qsy为板由屈曲产生的剪力，Mx和Mxy等为板由屈曲产生的弯矩和扭矩.

板的弹性屈曲临界荷载可认为是板平衡微分方程的多值性问题.在弹性范围内正交异形板的平衡微分方程可根据小挠度理论、板的物理方程、几何方程和力的平衡进行求解.

1.2 平衡微分方程

根据小挠度理论基本假定和力的平衡关系，各中面力在x 和y 方向的分力为零，仅存在z 方向的分力，由图1 可知各中面力在z 方向的分力如式（1）～式（3）所示.

Fx在z 方向的分力为：

Fy在z 方向的分力为：

Fxy在z 方向的分力为：

薄板发生屈曲时，产生的剪力在z 方向上的合力如式（4）所示.

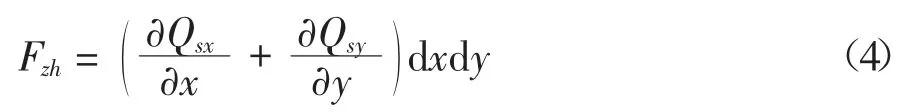
根据z 方向上各力的合力为0，得到式（5）.

根据图1（b），分别对x 轴和y 轴取矩并略去高阶微分项，可得剪力与弯矩和扭矩的关系，如式（6）和式（7）所示.

将式（6）同时对y 偏导一次，式（7）对x 偏导一次，分别代入式（5）可得到板关于中面力、弯矩和扭矩的平衡微分方程，如式（8）所示.

式（8）中含有Mx、My、Mxy及ω 四个未知数，而根据正交异性板的物理方程和几何方程可得到力矩与竖向位移之间的关系，即可将式（8）简化为仅含有竖向位移ω 的微分方程.

波形钢腹板屈曲产生的弯矩和扭矩可表示为关于ω 的表达式[18]，如式（9）所示.

将式（9）代入式（8）可得到仅含有ω 的板的平衡微分方程，如式（10）所示.

式（9）和式（10）中，Dx和Dy为板在两个弹性主轴方向的抗弯刚度，Dk为板在弹性主轴的抗扭刚度，且有Dxy=2Dk+μkDy=2Dk+μyDx，对于波形钢腹板，Dx、Dy和Dxy的表达式如式（11）所示[14].

式中：E 为波形钢腹板的弹性模量；Iy为单个周期波对y 轴的惯性矩，Iy=2a1t；q 为单个周期波的投影长度，q=2（c+a1）；s 为单个周期波的展开长度，s=2（a1+a2）；μ 为波形钢腹板的泊松比，其余符号的相关含义如图2 所示.

图2 波形钢腹板的截面尺寸Fig.2 Structure of corrugated steel web

2 波形钢腹板弹性整体剪切屈曲强度

2.1 整体剪切屈曲强度理论分析

纯受剪状态下的整体剪切屈曲的波形钢腹板计算简图如图3 所示，图3 中l 为波形钢腹板的计算长度，h 为波形钢腹板的高度.

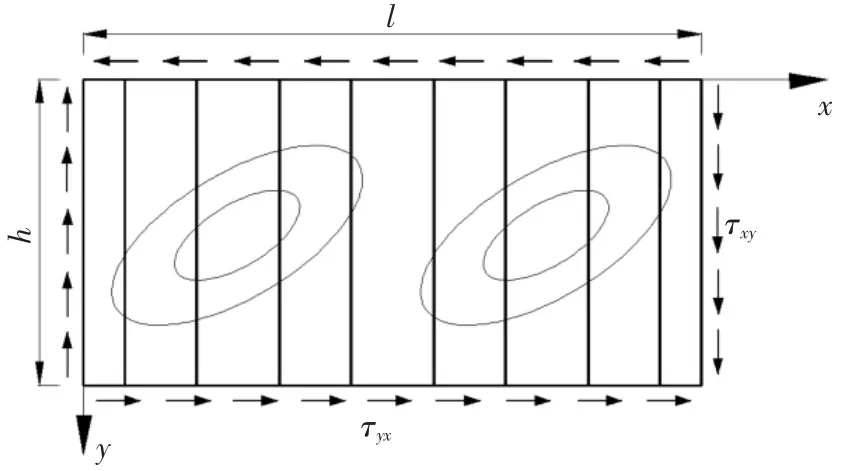
图3 波形钢腹板弹性屈曲强度计算简图Fig.3 Calculation diagram of elastic buckling strength of corrugated steel web

运用伽辽金法求解纯受剪波形钢腹板弹性整体剪切屈曲强度时，无需求解板的总势能，可直接利用板在屈曲时的平衡微分方程，并假定满足板几何边界条件和位移边界条件的位移形函数从而建立伽辽金方程组进行求解[19].

假定波形钢腹板屈曲时的位移形函数ω（x）如式（12）所示：

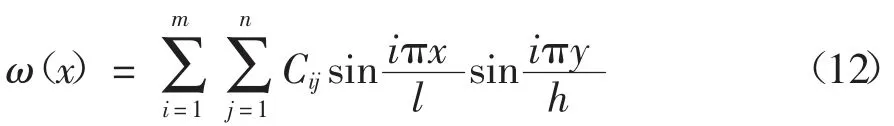
对于纯剪状态下的波形钢腹板，Fx=Fy=0，则平衡微分方程根据式（10）可表示为：

则伽辽金方程组可表示为：

将式（12）代入式（13）进行偏导运算，联立式（13）的计算结果和式（14），注意到

则式（14）可简化为：

式（16）在i±r、j±s 为奇数时成立.当对i、j、r 和s分别取值，可得到关于Cij的伽辽金方程组，其中Cij为非零参数，要想得到方程组的非零解，则只能有Cij构成的系数矩阵的行列式=0.通过计算Cij的系数矩阵行列式可得到一系列Fxy的计算值，其中绝对值最小的非零解为波形钢腹板的弹性整体剪切屈曲荷载，由式（17）可得到波形钢腹板的弹性整体剪切屈曲强度

由上述方法计算求得的波形钢腹板的弹性整体屈曲临界荷载为近似值，其精度与Cij系数矩阵行列式的阶数有关.当对i、j、r 和s 分别取值计算发现，Cij系数矩阵行列式可分为两组，当i+j 为奇数时为一组，当i+j 为偶数时为另一组，并由计算可知，当i+j 为偶数时，求得波形钢腹板弹性整体屈曲临界荷载值最小.限于篇幅，本文仅对i+j 为偶数时Cij的系数矩阵行列式进行计算分析.本文在计算波形钢腹板的弹性整体屈曲强度时，式（12）中取m=n=5，并根据式（16）的成立条件，对（i，j）和（r，s）取如表1 所示的组合形式.

表1 （i，j）与（r，s）取值表Tab.1 （i，j）and（r，s）values

根据表1 中（i，j）和（r，s）的组合形式，计算式（16）并令，求得系数矩阵C 的行列式如式（18）所示：

2.2 理论计算与数值计算对比分析

为了验证理论公式的正确性，选取文献[16]中算例进行数值模拟，其波形钢腹板的波形尺寸，如表2所示.

表2 波形尺寸Tab.2 Dimension of trapezoidal corrugated

图4 ANSYS 模型边界约束及加载图Fig.4 Boundary constraint and loading diagram of ANSYS model

规范中波形钢腹板弹性整体剪切屈曲强度的计算公式如式（19）所示.

式中：β 为波形钢腹板约束程度相关的系数，当边界条件为四边简支时取1.0，当四边固定时取1.9；Ix=t3（δ2+1）/6η，δ=d/t，η=q/s，Iy=t3/（12（1 -μ2））.

将式（18）中系数矩阵C 的行列式分别取6×6、8×8、10×10 和12×12 计算得到的波形钢腹板整体屈曲强度，将本文结果与有限元结果和规范计算结果进行了对比，如图5 所示.

图5 计算结果对比图Fig.5 Comparison of calculation results

从图5 可以看出，波形钢腹板弹性整体剪切屈曲强度本文方法值与ANSYS 有限元值的变化趋势一致，当波形钢腹板的高度一定时，随着波形钢腹板长度l 的增加，波形钢腹板的屈曲强度逐渐降低，由于规范中未考虑波形钢腹板的长度，故规范计算结果仅与波形钢腹板的波形、边界条件及高度有关，与波形钢腹板的长度无关.对本文计算方法，计算结果精度与式（19）中ζ1、ζ2、ζ3及Fxy的系数有关，ζ1、ζ2、ζ3及Fxy的系数与波形钢腹板挠曲位移函数中m、n 的取值有关，且m、n 的取值又决定式（18）的计算阶数，因此，m、n 取值较小或较大均影响式（18）的计算结果精度.当式（18）取6×6 阶的行列式时，本文方法计算值与ANSYS 有限元计算值的最大误差为33.05%，最小误差为30.90%；当式（18）取8×8 阶的行列式时，二者的最大误差为4.89%，最小误差为0.07%；当式（18）取10×10 阶和12×12 阶的行列式时，本文方法值与有限元值的最大误差为63.55%，最小误差为54.76%.由于m、n 的取值大小对ζ1、ζ2、ζ3及Fxy系数的影响并非倍数或指数的增减，因此，整体剪切屈曲强度的计算结果精度与式（18）的阶数增减不存在规律性.综上所述，当Cij的矩阵行列式阶数为8×8 时，本文计算方法计算的波形钢腹板整体屈曲强度更精确；而对于规范，由于忽略了Dxy对波形钢腹板弹性整体剪切屈曲强度的贡献，故规范的计算结果偏保守，规范计算结果与有限元结果的最大误差为45.48%，最小误差为39.87%.因此，利用本文理论计算波形钢腹板的整体剪切屈曲强度时应将Cij的矩阵行列式阶数为8×8.

2.3 理论计算与试验计算对比分析

通过上述分析可知，式（18）取8×8 阶行列式计算波形钢腹板的剪切屈曲时，计算结果与有限元结果吻合良好.为进一步验证本文方法的准确性，以文献[21]中两组发生弹性整体剪切屈曲的波形钢腹板试验梁的试验结果为工程背景，将式（18）的8×8 阶行列式计算值与试验值进行对比.两组试验梁的波形钢腹板波纹型号几何参数如表3 所示，两组试验梁波形钢腹板高均为609.6 mm，长均为304.8 mm.将本文结果与文献[21]的试验结果进行对比，如表4所示.

表3 文献[21]试验梁几何参数Tab.3 Geometric parameters of test girders in literature

表4 计算值和试验结果对比Tab.4 Comparison between calculation and test

从表4 可以看出，本文结果与试验结果吻合良好，其误差在5%以内，进一步验证了本文所提方法的正确性.

3 波形钢腹板剪切屈曲敏感性分析

本节分析了波形钢腹板型号、波形钢腹板的厚度和梁高对波形钢腹板剪切屈曲性能的影响。

3.1 已建桥梁所用波形钢腹板及梁高

国内外通用的波形钢腹板波纹型号、波形钢腹板厚度和梁高变化分别如表5 和表6 所示.

于是，我们不妨在建群之初，召开线上或线下家长会，和家长们明确各阶段建立家长群的目的和意义，统一思想；联合家长委员会，共同商议和制订《班级群管理与使用意见》等规则。例如，老师在发布标注有“不需回复”的信息后，家长不必回复“收到”或点赞、感谢；老师在发布标注有“收到需回复”的信息后，家长自动以“接龙”形式回复；重要的公共信息在群里发布，个别情况与问题私信沟通、解决等。还可明确不得在班级群内发布涉及隐私的信息，不得发布与本群无关的内容，不得进行人身攻击等要求，用科学管理保证高效沟通，还班级群一方净土。

表5 波形钢腹板波纹型号和厚度Tab.5 Corrugated type and thickness of corrugated steel web

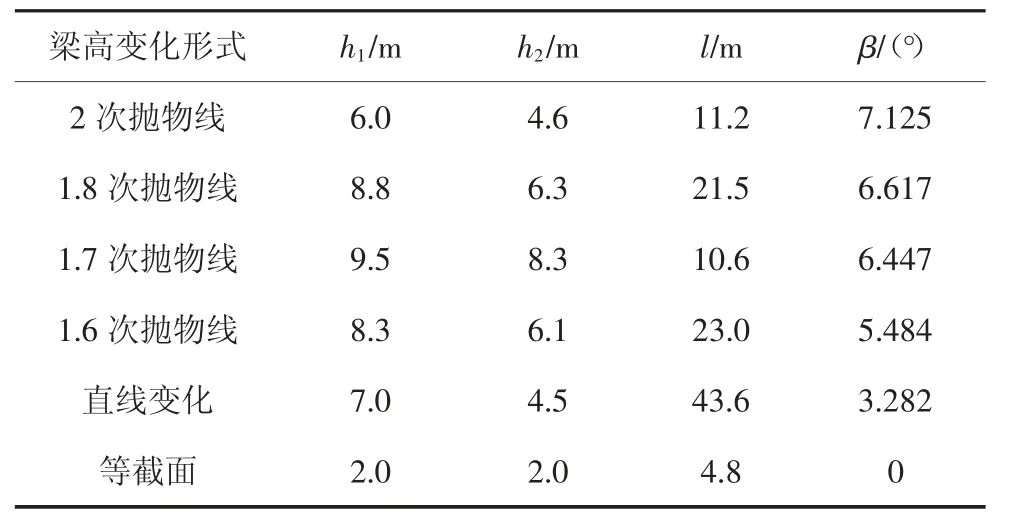
表6 梁高变化形式Tab.6 Variation form of girder height

从表5 可以看出，国内外通用的波形钢腹板波纹型号共10 种，分别为700 型、900 型、1000 型、1120 型、1200 型、1260 型、1500 型、1600 型、2000型和2400 型.其中2400 型是文献[22]提出的一种新型波纹型号，还未将其运用于实际工程中.

从表6 可以看出，实际桥梁建设中一共有6 种梁高变化形式.而在实际的波形钢腹板-混凝土组合梁中，中跨一般设置4 道或4 道以上的横隔板，因此，表6 中l 取主墩顶变截面抛物线起点处至跨间相邻横隔板间波形钢腹板长度，h1为墩顶处梁截面高度，h2为第一道横隔板处梁截面高度，以β 近似表示梁底与水平方向的夹角.

3.2 波纹型号对变截面波形钢腹板剪切屈曲的影响

以表5 中10 种波纹型号为例，选取表6 中梁高以2 次抛物线变化的波形钢腹板，腹板高度及长度如表6 中所示，腹板厚度选取24 mm，运用ANSYS建立有限元模型进行特征值屈曲分析，得到各波纹型号的屈曲模式和屈曲特征值如表7 所示.

表7 不同波纹型号的屈曲模式及特征值Tab.7 Buckling modes and characteristic values of different corrugated models

从表7 可以看出，对于上述10 种波纹型号的变截面波形钢腹板，由于2000 型和2400 型波纹型号相对其他8 种波纹型号波纹较疏，容易发生合成屈曲，其余8 种波纹型号均发生整体屈曲，屈曲特征值总体呈现先增大后减小的趋势.各波纹型号的变截面波形钢腹板剪切屈曲强度的变化趋势如图6 所示，整体屈曲与合成屈曲的屈曲模式示意图如图7所示.

图6 不同波纹型号屈曲强度变化趋势Fig.6 Trend of buckling strength of different models

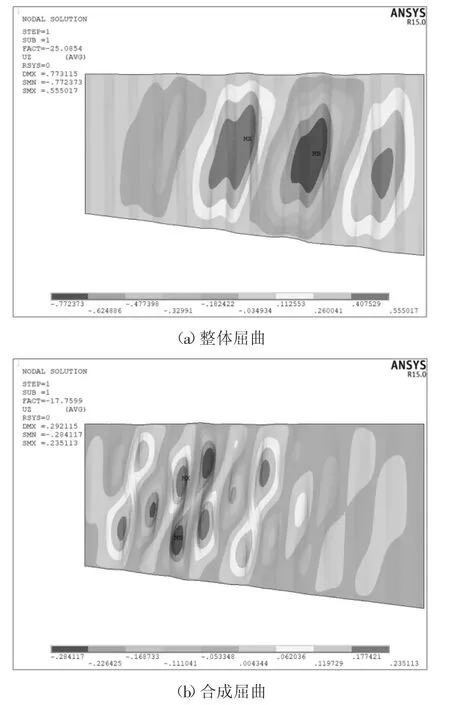
图7 不同波纹型号屈曲模式示意图Fig.7 Schematic diagram of buckling modes of different corrugated models

从图6 可以看出，对于不同波纹型号的变截面波形钢腹板，剪切屈曲强度与屈曲特征值的变化趋势一致，总体呈现先增大后减小的趋势，1600 型的波形钢腹板剪切屈曲强度达到较大值，其中1120 型、1500 型波形钢腹板分别较1000 型和1260 型的波形钢腹板剪切屈曲强度有所减小，分别减小了15.53%和3.58%.

通过对上述不同波纹型号的变截面波形钢腹板的计算分析，对于大跨度的变截面波形钢腹板-混凝土组合连续梁桥或连续刚构桥，1600 型的波形钢腹板为最优选择.

3.3 腹板厚度对变截面波形钢腹板剪切屈曲影响

在上述1600 型变截面波形钢腹板的基础上，选取不同的腹板厚度对变截面波形钢腹板剪切屈曲强度进行研究分析.考虑到大跨度变截面波形钢腹板连续梁桥的腹板厚度均较大，所以在本节研究中，波形钢腹板的厚度选16～30 mm，并按2 mm 公差递增，计算得到不同厚度的1600 型变截面波形钢腹板的一阶屈曲模式和屈曲特征值如表8 所示.

表8 不同腹板厚度的屈曲模式及特征值Tab.8 Buckling modes and characteristic values of different web thicknesses

从表8 可以看出，对于不同厚度的1600 型变截面波形钢腹板，随着腹板厚度增加，一阶屈曲模式由合成屈曲向整体屈曲变化，屈曲特征值逐渐增大.各种厚度的1600 型变截面的剪切屈曲强度变化趋势如图8 所示.

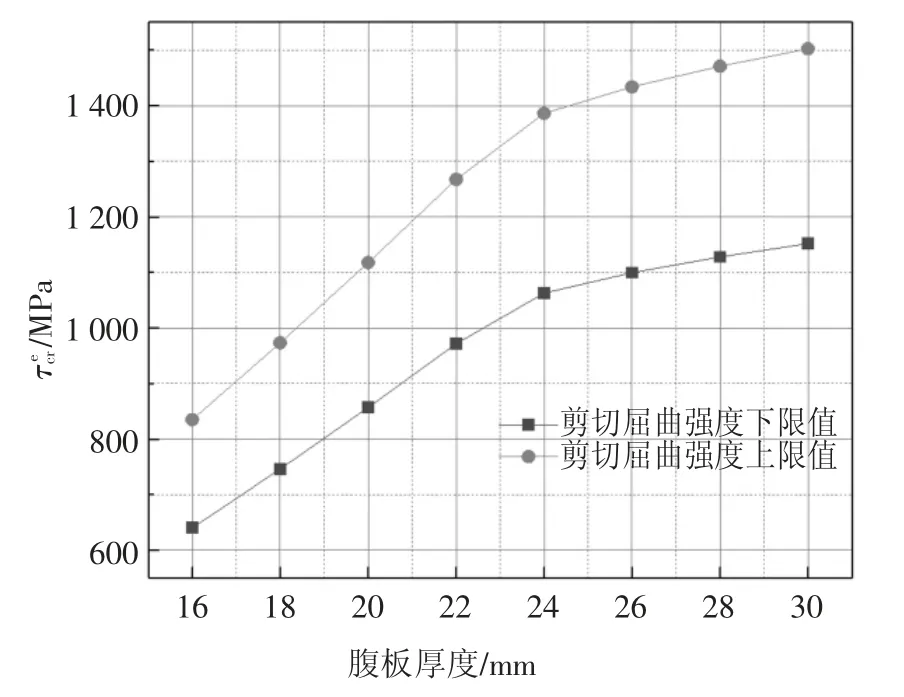
图8 不同腹板厚度屈曲强度变化趋势Fig.8 Trend of buckling strength of different web thicknesses

从图8 可以看出，随着波形钢腹板厚度的增加，波形钢腹板的剪切屈曲强度逐渐增大，弹性剪切屈曲临界力逐渐提高；但当波形钢腹板的厚度大于24 mm 时，即发生整体剪切屈曲时，弹性剪切屈曲强度的变化速率较发生合成屈曲时的剪切屈曲强度增长率逐渐减小，变化趋于平缓.

故对于大跨度变截面波形钢腹板，腹板厚度在16～24 mm 时，波形钢腹板的抗屈曲性能较高，在实际桥梁设计中可优先选择此范围内的板厚.

3.4 梁高变化对变截面波形钢腹板剪切屈曲影响

在研究梁高变化形式对变截面波形钢腹板弹性屈曲稳定性的影响时，以等截面波形钢腹板作为梁高变化形式的特例，采用1600 型波形钢腹板为例建立ANSYS 有限元模型，建立有限元模型时各波形钢腹板h1均取6 000 mm，l 均取11.2 m，板厚取24 mm，梁高变化形式如表6 所示.不同截面形式的波形钢腹板屈曲形式和屈曲特征值如表9 所示.

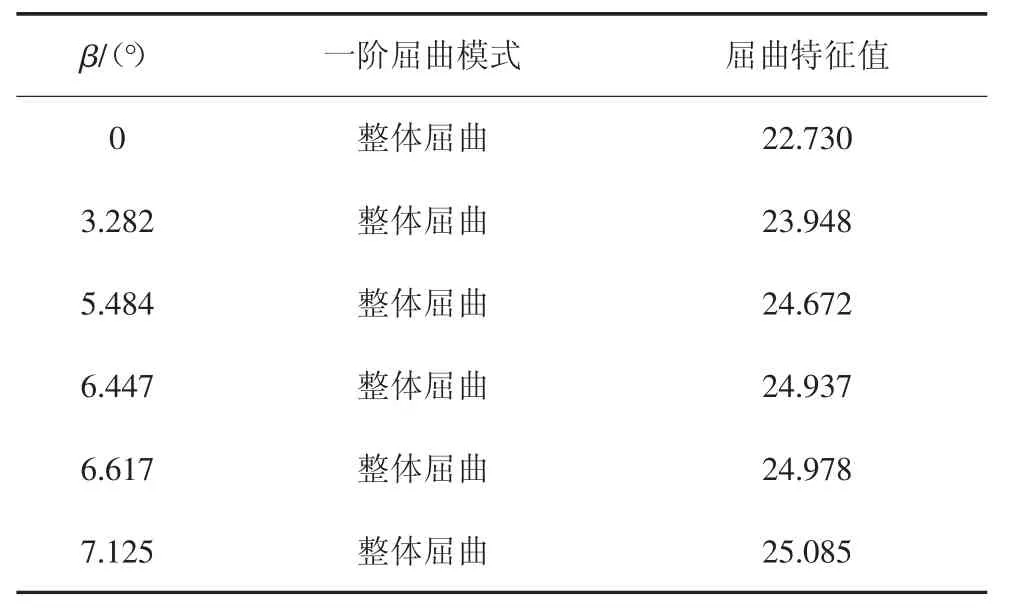
表9 不同截面高度的屈曲模式及特征值Tab.9 Buckling modes and characteristic values of different section heights

从表9 可以看出，1600 型不同梁高变化形式的波形钢腹板，变截面波形钢腹板的屈曲特征值高于等截面波形钢腹板的屈曲特征值，β 为7.125°的波形钢腹板较β 为0 的波形钢腹板屈曲特征值增加了10.36%；而对于变截面波形钢腹板，随着β 的增大，变截面波形钢腹板的屈曲特征值增加，β 为7.125°的变截面波形钢腹板屈曲特征值较β 为3.282°的变截面波形钢腹板屈曲特征值增加了4.75%.不同梁高变化形式的波形钢腹板弹性剪切屈曲强度变化趋势如图9 所示.

图9 不同截面高度的屈曲强度变化趋势Fig.9 Trend of buckling strength of different section heights

由图9 可以看出，随着β 值的增大，波形钢腹板的弹性剪切屈曲强度逐渐增加，但其上限值与下限值的比值逐渐减小，波形钢腹板的屈曲区域有向较大截面移动的趋势，如图10 所示，β 值分别为3.282°和7.125°的变截面波形钢腹板一阶屈曲模式图，因此对于高度较大的变截面波形钢腹板，应对主墩高腹板区腹板加强以防止发生屈曲破坏.

图10 不同β 值的一阶屈曲模式图Fig.10 First order buckling mode of different β value

4 结论

通过对变截面波形钢腹板的弹性整体剪切屈曲强度进行分析，可得到如下结论：

1）文中所推导的波形钢腹板弹性剪切屈曲强度的计算公式的计算结果与有限元的计算结果吻合良好，其中Cij的系数矩阵行列式取8×8 阶时，计算的变截面波形钢腹板弹性整体剪切屈曲强度的精度最高.

2）对于不同波纹型号的变截面波形钢腹板，在相同荷载和边界条件下，1600 型的波形钢腹板剪切屈曲强度达到最大值，因此对于大跨度的变截面波形钢腹板-混凝土组合梁桥连续梁桥或连续刚构桥，建议选用1600 型的波形钢腹板.

3）对于腹板厚度在16～24 mm 之间的1600 型变截面波形钢腹板，其抗屈曲性能较高，因此在实际桥梁设计中可优先选用此范围内的板厚.

4）对于主墩顶处腹板高度相同，并且计算长度相同的不同截面变化形式的波形钢腹板，变截面波形钢腹板的弹性剪切屈曲强度高于等截面波形钢腹板的弹性剪切屈曲强度，并且随着β 值的增大，波形钢腹板的弹性剪切屈曲强度逐渐增加，但弹性剪切屈曲强度的上限值与下限值的比值逐渐减小，波形钢腹板的屈曲区域有向较大截面移动的趋势.因此，对于高度较大的变截面波形钢腹板，应对主墩高腹板区腹板加强以防止发生屈曲破坏.