基于Herschel-Bulkley 流变模型的盾构螺旋输送机保压性能
2021-12-01杨益李兴高李兴春苏伟林
杨益,李兴高†,李兴春,苏伟林
(1.北京交通大学 土木建筑工程学院,北京 100044;2.城市地下工程教育部重点实验室(北京交通大学),北京 100044;3.五邑大学 信息工程学院,广东 江门 529020)
随着我国城市轨道交通建设的快速推进,在实践中土压平衡式盾构穿越区的地质水文条件愈加复杂,这对盾构螺旋输送机的排土、保压及调压作用提出了更高的要求.土压平衡式盾构施工时要求开挖的土体通过螺旋输送机以膏体的形式从压力土仓输送至盾构主机外的常压环境中.在输送过程中,渣土需要提供足够的保压能力来平衡螺旋输送机两侧的压力,以实现对土仓压力的控制,进而保证开挖面土体的稳定.因此,准确预估其保压性能对盾构安全掘进的控制起着至关重要的作用.
在螺旋输送机内压力分布特征的理论研究方面,Chung[1]假设作用在螺旋叶片及筒壁上的剪切应力为常数,得到螺旋输送机沿程压力梯度呈线性规律.Yoshikawa[2-3]分别假定渣土为摩擦型材料和塑性材料,依据提出的螺旋输送机压力梯度理论计算模型,得到了螺旋输送机沿程压力梯度分别呈现非线性和线性趋势,并深入探讨了不同转速条件及不同几何参数下的沿程压力梯度分布规律.Talmon 和Bezuijen[4]假设渣土为均匀塑性糊状介质,并且其剪切应力为常数,推导出螺旋输送机压力梯度具有线性分布的特点.随着试验手段的进步,通过模型试验探究螺旋输送机工作机制已成为可能.Peila 等[5]利用螺旋输送机模型装置,对泡沫改良中等粒径砂土进行了排土试验.Merritt 和Mair[6]针对黏土类渣土,利用螺旋输送机模型进行了排土试验,证实总应力沿螺旋输送机呈线性分布的规律.Kim 等[7]通过模型试验探究了螺旋输送机的螺距、叶片角度及转速等参数对出土量的影响.近年来,为进一步了解螺旋输送机内渣土的运动状态,渣土被假定为黏塑性流体用于数值计算中,为方便计算,目前常用的黏塑性流体模型为Bingham 模型[8-9].
综上所述,虽然目前的研究成果已较为丰富,但现有理论模型中,关于螺旋叶片及筒壁上的剪切应力的假设尚存在争议,而模型试验存在操作难度大、成本高且流动状态不可见等问题,因此,通过理论分析及模型试验估计螺旋输送机的保压性能仍十分困难,数值手段成为解决该问题的新途径.本文基于Herschel-Bulkley 流变模型(H-B 模型),探究了渣土流变参数及螺旋输送机工作参数对螺旋输送机保压性能的影响规律,并通过模型试验验证了计算结果的准确性,以期为更好地解释螺旋输送机的保压机制并准确预估及优化其保压性能提供理论依据.
1 理论基础
1.1 渣土流变模型
为满足盾构施工时建立土压平衡、防喷涌、防泥饼以及设备减磨的技术需求,开挖下来的渣土需呈塑性流动状态[10].同时,合理的渣土状态能为螺旋输送机提供均匀的压降梯度[9].近年来,随着对塑性流动状态的深入认识,渣土被认为是一种黏塑性流体[11-12].当剪应力小于屈服应力时,黏塑性流体表现出类似于固体的行为;但是,当超过屈服应力时,它将类似于流体流动[13].工程中常用的黏塑性模型包括Bingham 模型和H-B 模型.其中Bingham 模型最常见[14],而H-B 模型由于其广泛的适用性,常被用来描述新拌混凝土[15]、泥浆[16]、含颗粒悬浮液[17]等材料,其剪应力τ 与应变率的关系可以写成:

式中:τ0为屈服应力;k 为黏度指数;n 为幂律指数.Bingham 模型是H-B 模型在n=1 时的特例.
孟庆琳等[12]通过自制的土体旋转流变仪证实泡沫改良砂土的流变行为可用Bingham 模型描述.但除泡沫外,膨润土和高分子聚合物也是常用的改良剂[18],根据Yang 等[19]和Jeong 等[20]的研究,若土样或改良剂中存在黏土成分,则其流变行为更符合H-B模型.因此,采用H-B 模型能够更加准确地描述更多种类渣土的流变行为.
1.2 螺旋输送机保压原理
土压平衡式盾构属于闭胸式隧道掘进设备,开挖后的渣土经过改良形成良好的传力介质,将来自千斤顶的推力传递至开挖面,用以平衡开挖面的土压力ps和水压力pw.螺旋输送机有两方面的作用:①从土仓内排出渣土;②通过渣土的运动使土仓压力pe沿螺旋输送机逐渐衰减,以实现保持土仓内压力的稳定,即保压作用;③通过调节转速,控制出土量,调节土仓压力pe,即调压作用.图1 所示为螺旋输送机工作机制示意图.

图1 螺旋输送机工作机制示意图Fig.1 Working mechanism of screw conveyor
渣土压力从螺旋输送机入口A 到出口B 逐渐下降,在出口处降低为零或较小的量值,保证出渣过程稳定可控.假定渣土在螺旋输送机内的流动连续且恒定,同时忽略渣土的压缩性,则根据伯努利方程,图1 中A 点与B 点的机械能应遵循:

式中:P 为渣土压力;ρ 为渣土密度;v 为渣土运动速度;h 为高度;ΔE 为机械能损失项.由于螺旋输送出入口面积相等,因此,根据连续性原理,出入口的渣土速度vA和vB相等,公式(3)可变形为:

由公式(4)可知,螺旋输送机的保压能力来源于两方面:①通过向上的输送,将压能转化为重力势能;②通过渣土的摩擦消耗,将压能最终转化为内能.ΔP 越大,则表明螺旋输送机的保压性能越优异.
重力势能的大小取决于渣土的密度ρ 以及出入口的高度差hB-hA,高度差可根据螺旋输送机长度L以及安装角度α 计算:

渣土本身黏性摩擦力的存在是产生ΔE 的根本原因.若将螺旋输送机内的渣土看作控制体,则ΔE可表示为:

当忽略渣土压缩性时,根据广义牛顿内摩擦定律,应力张量σij与应变率张量sij的关系可表示为:

式中:p 为压力函数;δij为克罗内克符号;μ 为渣土的动力黏度.
由公式(6)(7)可知,ΔE 由渣土的应力场及速度场决定.渣土的应力场与渣土材料本身的动力黏度μ 直接相关.但是,由于螺旋输送机本身复杂的结构型式,无法通过解析方法求得ΔE,需要借助数值模拟的手段.在模拟过程中,μ 为非定值,可用H-B 流变模型进行描述:

渣土的速度场则与螺旋输送机的转速及出渣效率有关.根据图1 所示的螺旋输送机的几何结构,实际出渣体积流量为:

2 数值建模
2.1 计算模型及网格划分
为尽量贴合实际,本文选取的计算模型为直径6 m 的盾构机的螺旋输送机模型.如图1 所示的几何结构,总长度L=10 m,螺旋直径D=0.8 m,螺旋轴直径d=0.2 m,螺距l=0.7 m,叶片厚度s=60 mm,共14节螺旋.采用Solidworks 软件建立螺旋输送机的三维几何模型,并将其导入Fluent 软件中进行网格划分.模型采用多面体网格,由四面体网格转化而成,在保证网格质量的基础上,极大地提高了计算效率.整个流体域网格数目约为19 万,网格密度如图2 所示.
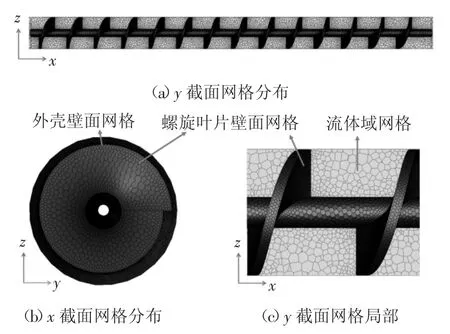
图2 网格密度分布Fig.2 Grid distribution
由于数值建模的目的在于求解螺旋旋转条件下渣土的机械能损失ΔE,模型中的螺旋叶片及流体域的网格均假定为匀速旋转状态,因此采用多重参考系法(MRF)对模型进行定常流计算.螺旋输送机内的流体域设置为动区域,其他区域为静区域;螺旋叶片为动壁面,外壳为静壁面.动区域及动壁面按照螺旋输送机转速设置旋转.
2.2 计算条件
本文算例选用层流模型,入口条件设置为压力入口,压力值为0.2 MPa,出口采用流量出口,流量值根据公式(10)计算,壁面均采用无滑移壁面条件,即默认渣土在壁面处与壁面的相对速度为零.内迭代步设置为300 步,可满足残差下降两个量级.
由1.2 节的分析可知,影响ΔE 的因素来自两个方面:①渣土的H-B 流变模型参数,即屈服应力τ0,黏度指数k,幂律指数n;②螺旋机工作参数:转速r,出渣效率η.根据文献[12,19]的流变试验测试结果,表1 给出了不同类型的渣土流变参数的取值参考.计算参数具体取值见表2,所有工况中临界剪切率均取0.01 s-1.转速r 的取值则依据实际螺旋输送机的设计工作参数.出渣效率η 为非人为调控参数,其取值可通过施工监测获得,依据现有的报道[21-22],本文中η 取值40%~100%,涵盖了大部分的螺旋输送机工作状态.计算中考虑重力的影响,渣土密度为2 000 kg/m3,重力方向按照螺旋输送机安装角度α=20°进行设置.
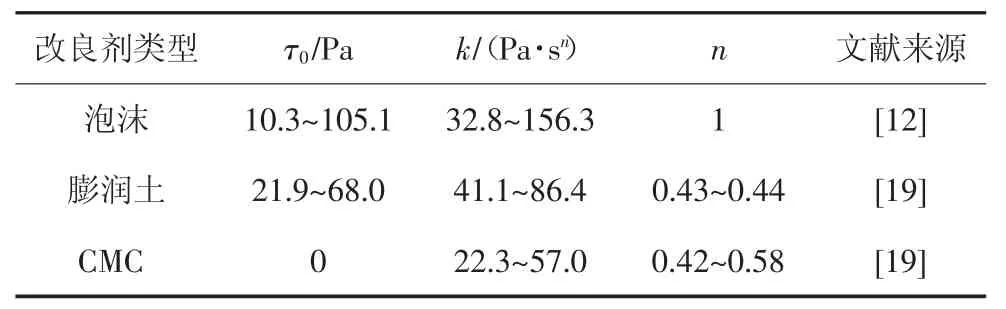
表1 渣土流变参数取值参考Tab.1 Reference value of rheological parameters

表2 计算工况Tab.2 Simulation cases
3 结果分析
3.1 渣土流动规律
以表1 中的对照组为例,计算结果如图3 和图4所示.图3(a)(b)(c)分别为渣土的压力、速度、剪切率分布云图.
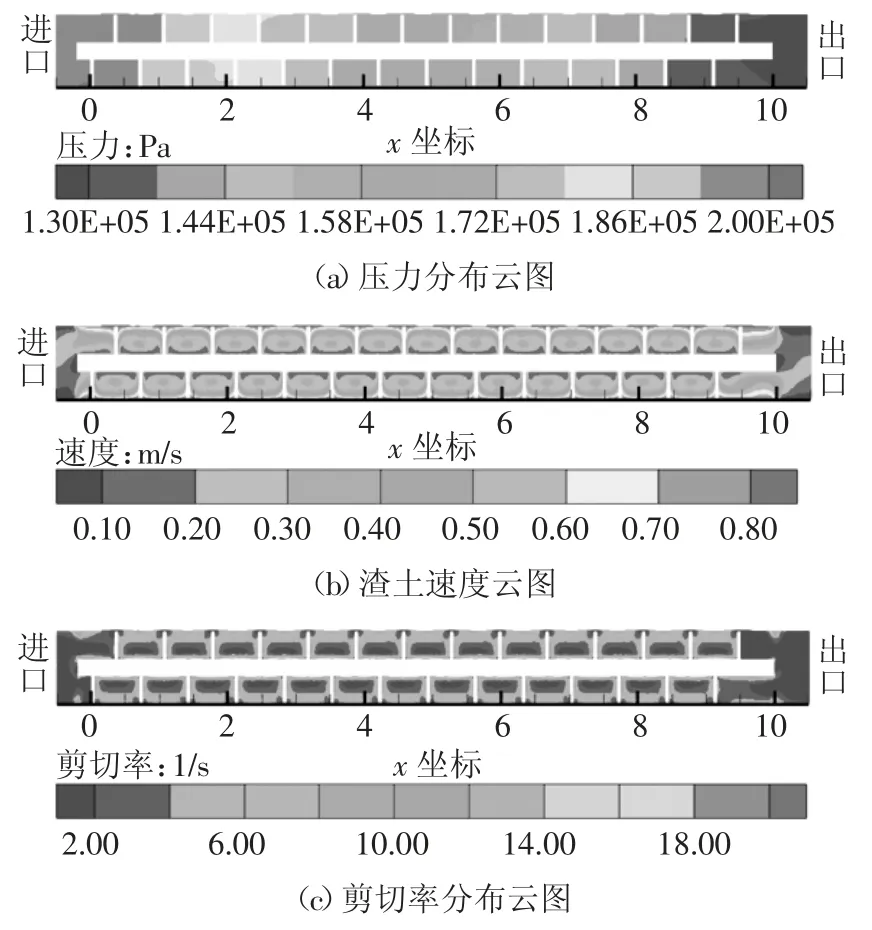
图3 对照组渣土的计算结果Fig.3 Results of conditioned soil in control group
由图3(a)可知,渣土压力沿x 正方向递减,螺旋输送机内同一x 截面处压力值相差不大.数值计算中的压力为位置势能与压能的总和,因此进出口的压差即为公式(3)中的ΔE,而非ΔP.由图3(b)可知,螺旋输送机内渣土的流动速度并不均匀,在螺旋叶片的带动下,越靠近叶片外缘,渣土的流速越大,渣土流速的变化范围为0~0.9 m/s.由图3(c)可知,螺旋输送机内渣土的剪切率并不恒定,由于渣土被假定为H-B 塑性材料,这意味着渣土内部剪应力随螺旋位置产生变化.剪切率主要变化范围为10 s-1以下,仅在转轴附近局部超过10 s-1.
图4 为螺旋叶片的压应力、剪应力分布云图.由图4(a)可知,在旋转状态下,越靠近叶片外缘,剪应力越小,而叶片内缘及转轴位置剪应力较大,每节螺旋叶片的剪应力分布基本相同.由图4(b)可知,螺旋叶片的压应力分布与图3(a)中渣土压力分布呈现相同的规律,压应力沿x 轴线方向线性递减.

图4 对照组螺旋叶片的计算结果Fig.4 Calculation results of screw in control group
3.2 渣土流变参数对保压性能的影响
在螺旋输送机转速为20 r/min、出渣效率为60%的条件下,选取输送机外壳某位置沿x 轴线方向的压力变化为对象,探究不同渣土流变参数对保压性能的影响.图5(a)(b)(c)分别为屈服应力τ0、黏度指数k 及幂律指数n 对螺旋输送机保压性能的影响.由图5 可知,输送机外壳处压力沿x 方向呈阶梯状下降的分布规律.由于螺旋叶片的阻隔作用,导致压力在叶片位置产生明显下降,形成阶梯曲线的梯面部分;而在相邻两节叶片间的空隙处,压力下降不明显,形成阶梯曲线的踏面部分.螺旋输送机的压降值越大,表明其保压性能越优异.同一工况条件下,单节螺旋的压降值相同,因此,增加螺旋输送机的长度可提高螺旋输送机的保压性能.
从图5 可看出,τ0、k、n 越大,压力下降越显著.其中,τ0每增加30 Pa,进出口压差增加8.9 kPa;k 每增加40 Pa·sn,进出口压差增加33.1 kPa;n 值越大,螺旋输送机保压性能的提升幅度越大.三者中k 和n值对保压性能的影响较为明显,而τ0的影响较小.因此,为提高螺旋输送机的保压性能,可通过渣土改良提高其流变参数中的k 和n 值.
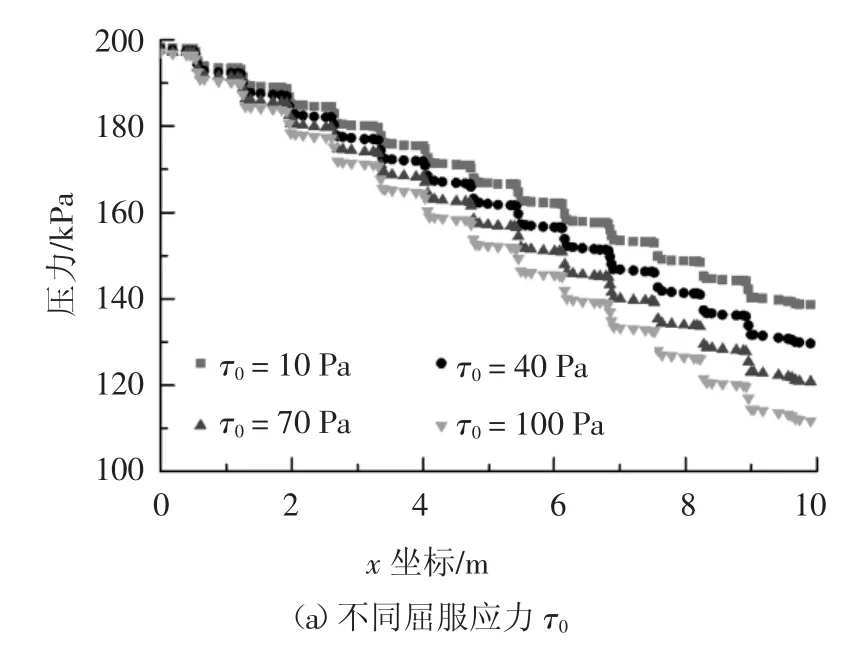
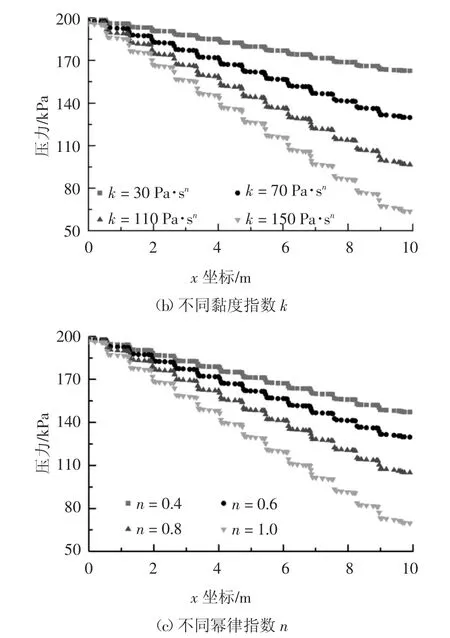
图5 不同渣土流变参数下压力随x 坐标的变化Fig.5 Changes of pressure with x-coordinate under different rheological parameters of soil
3.3 螺旋输送机工作参数对保压性能的影响
当保持渣土流变模型参数恒定时,不同螺旋转速r 和出渣效率η 对螺旋输送机机械能损失ΔE 的影响规律如图6 所示.由图6 可知,螺旋转速r 越大,出渣效率η 越高,则机械能损失ΔE 值越大,螺旋输送机保压性能越好.当η 固定不变时,随着r 增加,ΔE 基本呈线性增加,但增长幅度略有下降.由此可知,在实际施工过程中,可通过提高转速来增加螺旋输送机的保压能力.而当转速r 固定不变时,随着出渣效率η 增加,ΔE 也基本呈线性增加,并且r 值越高,ΔE 的上升幅度越大.在施工过程中,出渣效率η 并非人为可控因素,其大小与螺旋输送机进出口压差有关.当压差较大时,进口处压力推动渣土向外排出,此时出渣效率η 较高,渣土的机械能损失ΔE也较大,说明螺旋输送机的保压能力具有随土仓压力大小而自我调节的特点.
为更直接地表达ΔE 与r、η 间的对应关系,对图6 中的计算结果进行二元多项式回归,结果如图7所示.由图7 可知,二次多项式的回归结果与计算数据的拟合优度极高,确定系数R2高达0.999;而一次多项式的回归结果与计算数据的拟合优度相对略差,确定系数R2为0.970.为方便实际应用,一次多项式的回归模型亦可满足工程估测需要,即ΔE 与r、η 之间的关系可以表达为:
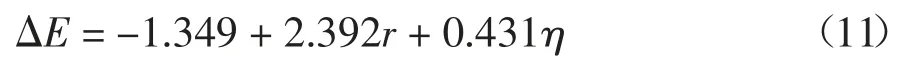

图6 机械能损失ΔE 与r、η 的关系Fig.6 The relationship between ΔE and r,η

图7 ΔE 的二元多项式回归估测结果Fig.7 Results of ΔE by binary polynomial regression
由于渣土的流变参数保持不变,因此螺旋转速r是通过改变渣土的速度场来影响机械能损失ΔE.螺旋转速越快,渣土的运动速度越快,摩擦力做功越高,进出口压差则越大.图8 和图9 分别为不同螺旋转速下螺旋输送机中心位置x 截面的流速与剪切率分布云图.由图8 可知,转速5 r/min 和20 r/min 条件下渣土的流速具有相似的分布规律,在螺旋叶片的带动下,越靠近圆筒外缘,渣土流速越高.但二者流速大小有明显区别,转速5 r/min 时最大流速仅0.2 m/s,而转速20 r/min 时最大流速为0.8 m/s.由图9可知,不同转速下渣土剪切率的分布规律几乎完全一致,剪切率大小与螺旋转速大小成正比.由此可知,当螺旋转速增加时,渣土的流速及剪切率随螺旋转速成比例增加,但由于公式(8)中H-B 模型的动力黏度μ 与剪切率之间为非线性关系,因此图6 中ΔE 值不随螺旋转速r 增加而线性增长.

图8 不同螺旋转速下x 截面渣土流速分布云图Fig.8 Velocity distribution of soil in x cross section under different screw rotation speeds

图9 不同螺旋转速下x 截面渣土剪切率分布云图Fig.9 Shear rate of soil in x cross section under different screw rotation speeds
图10 所示为不同出渣效率η 下x 截面渣土流速分布云图.由于螺旋转速r 相同,因此出渣效率η不同的成因是渣土的流速不同.由图10 可知,随着出渣效率增加,x 截面中出现月牙形的加速区,出渣效率η 越高,加速区越明显.出渣效率η 的影响因素较为复杂,显然仅依靠螺旋旋转产生的“抽力”难以在渣土中心区域形成加速区,加速区是在土仓压力的推动作用下形成的.当出渣效率在40%~60%之间时,加速区不明显,此时渣土的输送由螺旋旋转主导;当出渣效率在80%~100%时,加速区明显,此时渣土的输送受螺旋“抽力”及进出口压差共同作用.在实际应用中,出渣效率的确定可通过统计出渣量和螺旋输送机转速进行估计.

图10 不同出渣效率下x 截面渣土流速分布云图Fig.10 Velocity distribution of soil in x cross section under different soil conveying efficiency
图11 所示为不同出渣效率下x 截面渣土剪切率分布.由图11 可知,随着出渣效率η 增大,渣土剪切率整体呈增大趋势,局部区域出现明显增大.其中,转轴及外壳壁面附近剪切率增长最为明显,最大剪切率始终维持在20 s-1以内.因此,在进行渣土改良时,应重点关注剪切率在0~20 s-1范围内渣土的流变行为.


图11 不同出渣效率下x 截面渣土剪切率分布云图Fig.11 Shear rate of soil in x cross section under different soil conveying efficiency
3.4 螺旋输送机保压性能优化流程
根据以上分析,螺旋输送机的保压性能与渣土的流变行为及螺旋输送机的工作状态均密不可分.因此,在计算螺旋输送机保压性能时,需依据实际情况逐一判别,不可一概而论.图12 提供了螺旋输送机保压性能的优化流程,流程详细说明如下:
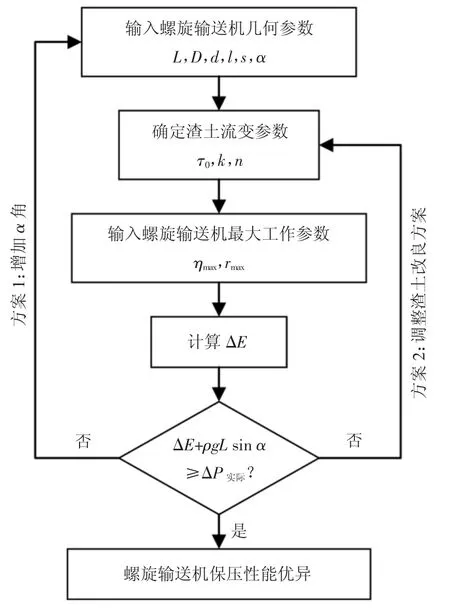
图12 螺旋输送机保压性能优化流程Fig.12 Optimization flow chart of pressure maintaining performance of screw conveyor
1)确定螺旋输送机的相关几何参数以用于数值建模.若螺旋输送机为双节螺旋结构,则也应按实际尺寸建立几何模型.
2)通过流变试验确定隧道穿越地层所产生渣土的H-B 流变模型参数,由于隧道可能穿越多种地层,应分别对经渣土改良后的不同类型渣土进行流变测试,取所有结果中的最小参数值作为最不利工况.
3)确定螺旋输送机的最大工作参数,其中最大转速rmax应依据螺旋输送机设计参数选取,而最大出渣效率ηmax宜取100%,当η 超过100%时,则可认为实际出渣量大于螺旋输送机自身的输送能力,此时螺旋输送机保压功能失效的风险将大大增加.
4)利用CFD 方法计算机械能损失ΔE.
5)若ΔE+ρgL sin α≥ΔP实际,即计算保压能力大于实际螺旋输送机进出口压差,说明保压性能优异.反之,则需要对保压性能进行优化,方案1 为增加输送机仰角α 值,若仍无法满足判定条件,则需要采取方案2,调整渣土改良参数,如更换改良剂种类或调整改良剂用量,直至满足判定条件.
4 试验验证
在数值计算中,渣土被假定为符合H-B 流变模型的假塑性流体,为验证这一假定的可靠性,特将计算结果与室内试验结果进行对比验证.采用如图13所示的螺旋输送机模型试验装置,螺旋机长度1.0 m,直径108 mm.模型机系统由渣土仓、倾斜螺旋机、联轴器、减速电机、变频器及水平方向加压系统组成.其中螺旋机外壳处分别等间距安装有6 个土压力计和6 个空隙水压力传感器,如图13 所示,用于测量法向应力和孔隙水压力.在试验过程中,当土仓内渣土逐渐减少时,加压系统的水平方向气缸以恒定压力向前推进,气缸始终与大型储气罐相连接,保证了螺旋输送过程中土仓压力始终维持恒定.根据土仓内渣土输送情况,可计算出渣土的出渣效率η.

图13 螺旋输送机模型试验装置Fig.13 Screw conveyor model machine
由于模型试验仅用于验证理论计算中基本假设的可靠性,因此试验中无需配置相似材料,试验材料为经改良后的普通渣土,改良渣土的配比及相关力学参数如表3 所示.膨润土浆液选用膨化24 h 的钠基膨润土浆液.改良渣土的塌落度值为190 mm,属于典型的“塑性流动状态”.根据文献[19]所述的测试方法,采用Brookfield R/S+型流变仪的十字板型转子系统VT-40-20 测试试验所用改良渣土的流变参数.渣土的流变试验结果如图14 所示,采用最小二乘法进行拟合,分别得到Bingham 模型和H-B 模型的拟合曲线,其中H-B 模型的确定系数R2高达0.998,而Bingham 模型仅为0.937,说明在模拟渣土流变行为方面,H-B 模型更为精确.螺旋输送机排出的渣土与试验前的状态基本一致,仅有少量膨润土浆液析出.试验共设置两种工况:工况1 螺旋输送机运行转速为16 r/min,渣土仓工作压力为200 kPa;工况2 螺旋输送机运行转速为6 r/min,渣土仓工作压力为100 kPa.待盾构螺旋机模型工作状态稳定后,根据渣土仓内的土样体积及出渣口排出的渣土体积,计算出两种工况下模型机平均出渣效率分别为79%和63%.

表3 改良渣土的质量分数及力学参数Tab.3 Mass fraction and mechanical parameters of conditioned soil
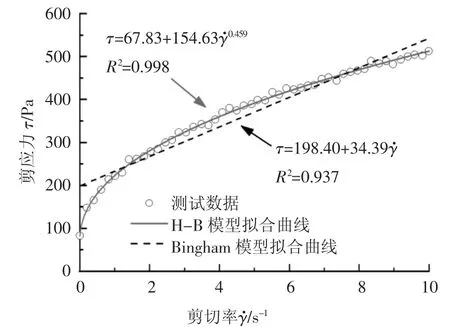
图14 改良渣土的流变试验结果Fig.14 Rheological test results of conditioned sand
依据模型试验机尺寸及参数进行数值建模和计算,理论计算与试验结果对比见图15.整体来看,两种工况下的理论计算结果与试验结果均较为吻合,说明H-B 模型用于模拟螺旋输送机内渣土的流动及力学性能是较为可靠的.工况1 中当x 坐标在0.6 m 和1.0 m 时,理论压力值较实测值偏大,其可能的原因为,理论计算中假设渣土为均质的黏塑性流体,忽略了渣土与管壁的相对滑移,而实际渣土中的固体颗粒与管壁存在摩擦,增加了机械能的消耗.此外,当x 坐标为1.0 m 时接近螺旋输送机出口处,两种工况下的实测压力值均存在突变,原因是螺旋机出口处突然泄压导致实测压力值较理论计算值更小,以致螺旋输送机保压性能的理论计算结果偏保守.

图15 计算与试验结果对比Fig.15 Comparison of calculation and experimental results
5 结论
1)螺旋输送机存在2 个保压途径,一是将土仓内的压能转化为渣土的重力势能,二是通过渣土的摩擦消耗,将压能最终转化为内能.重力势能转化量与螺旋输送机的长度L 及安装角度α 的正弦值线性相关,而因摩擦消耗产生的机械能损失ΔE 与渣土流变参数τ0、k、n 及螺旋输送机转速r、出渣效率η均密切相关.
2)采用CFD 方法在评价螺旋输送机保压性能方面有很大潜力.渣土的流变参数对螺旋输送机保压性能有较大的影响,其中H-B 模型的k 和n 值的影响最为显著.k 每增加40 Pa·sn,机械能损失ΔE 增加33.1 kPa;n 值越大,保压性能的提升幅度越大.
3)渣土摩擦消耗的机械能损失ΔE 与r 和η 基本呈线性关系,但随着转速r 增加,ΔE 的增长幅度略有下降.ΔE 与r、η 间基本符合一次多项式回归模型,在本文选取的计算条件下,函数形式可表示为ΔE=-1.349+2.392r+0.431η.
4)通过数值模拟结果与试验结果的对比,验证了H-B 模型用于模拟渣土流动和计算螺旋输送机保压性能的可靠性.依据数值计算结果,给出了螺旋输送机保压性能的优化流程,以期为施工过程中提高螺旋输送机保压能力以及渣土改良参数优化提供指导和依据.
