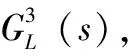一种拟Laguerre控制器设计
2021-12-01杨启文曾韵之胡兴燕薛云灿
杨启文,曾韵之,胡兴燕,薛云灿
(河海大学 物联网工程学院,江苏 常州 213022)
0 引言
正交级数,如勒让德(Legendre)级数、帕德(Pade)级数、傅里叶(Fourier),在函数逼近或拟合方面有着显著的优点[1-2]。正交级数虽然在理论上能够带来趋近于零的逼近误差,但作为控制器模型在自动控制系统中却不如PID控制器应用广泛。
拉盖尔(Laguerre)级数是一类L2(R+)上的正交级数。1932年Lee首次将其应用于瞬态问题研究[3],1956年Wiener提出了连续时间内的Laguerre级数,并将其应用于系统识别[4]。由于拉盖尔正交级数包含了系统阶次以及时延信息[5],因此在系统建模时,只需要根据误差精度选择合适的展开项,无需关注系统的真实模型结构,这使得拉盖尔级数在系统建模与辨识时[6-7],十分便利。
当前,将拉盖尔级数作为控制器使用时,仅局限于离散时间形式[8-9]:使用简单的p步超前预测控制律来预测过程响应,从而尽可能快地达到期望值[10-13]。在大规模、复杂系统中,每个子系统利用正交拉盖尔网络,实现分散预测控制[14]。也有学者将拉盖尔级数与工业中广泛使用的PID相结合,既保留了对时延和结构变化不敏感的拉盖尔函数模型特性,又结合分数阶PID控制的优点,实现基于拉盖尔模型的分数阶PID预测控制[15]。
考虑到拉盖尔级数在逼近方面的优势以及在连续时间控制器研究方面的不足,本文提出一种连续时间的拟拉盖尔控制器模型及其参数整定规则,并与工业过程中广泛使用的PID控制器进行对比研究,比较拟拉盖尔控制器与PID控制器在模型逼近和抗干扰方面的性能,为工业过程控制提供新型控制器模型。
1 拉盖尔级数
对于任意函数f(x),可以用如下的拉盖尔级数形式进行表示[16]:
(1)
式中,Ln(x)是由罗德里格公式推导得到多项式序列,Cn为拉盖尔系数:
拉盖尔级数的逼近精度随着展开项的增加而提高,当展开项趋近于无穷大时,逼近误差可以趋近于0,即:
由于存在如下关系:

因此,拉盖尔多项式序列Ln(t)构成了L2(R+)函数空间上一组完备的归一化正交基。
对于连续时间过程,拉盖尔级数通常定义为[17-18]:
(2)
其中:p为时间比例因子,t∈[0,∞)为时间变量。将式(2)进行拉普拉斯变换,便可得到式(3)所示的复数域拉盖尔级数:
(3)
复数域的拉盖尔级数形式,为构建动态系统输入/输出关系的传递函数模型提供了可能。
2 拟拉盖尔控制器模型
在经典控制理论中,通常将零初始条件下系统输出与输入的拉普拉斯变换之比,定义为一个线性系统的传递函数模型。根据式(3)所示的复数域拉盖尔级数,一个线性定常连续系统的传递函数模型可定义为:
(4)
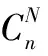
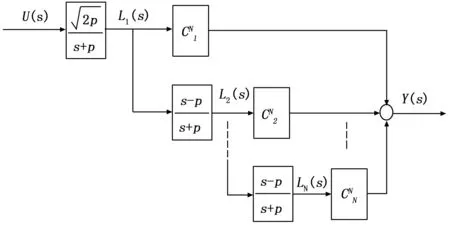
图1 复数域拉盖尔模型
在式(4)所示拉盖尔级数型传递函数模型中,由于p≠0,因此标准拉盖尔级数型传递函数是一个0型环节,无法描述含积分器环节的动态过程。0型环节的缺点是无法获得足够高的低频增益,如果将其作为控制器应用于反馈控制系统中时,那么当被控对象无积分特性时,必然会导致系统存在稳态误差。
为解决式(4)拉盖尔级数型传递函数的不足,同时又尽可能保留拉盖尔级数的基本特性,最直接的做法是在拉盖尔传递函数模型中串接一个积分器。但这种处理方式,会增加控制器的阶次和相角滞后,对系统的稳定裕度和快速响应性不利。
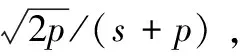
(5)
比较式(4)和式(5)可知,当展开项N的阶次相同时,拟拉盖尔控制器模型没有增加系统模型阶次,但相角增加了θ=arctg(ω/p)-0.5π;如果式(4)模型中采用串接积分器的方式,控制器的阶次不但会增加一阶,而且相角会增加-0.5 π,不利于提高系统的相角裕量。
3 拟拉盖尔控制器频率特性
拉盖尔级数的展开项越多,逼近精度越高。但过高的控制器阶次,一方面会带来性能冗余,另一方面也会导致参数整定和工程实现复杂。因此,大多数情况下,控制器的阶次尽可能低。
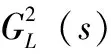
(6)
进行频域特性比较。
由式(5)知,当系统展开阶次N为2和3时,拟拉盖尔控制器模型可改写为如式(7)所示形式:
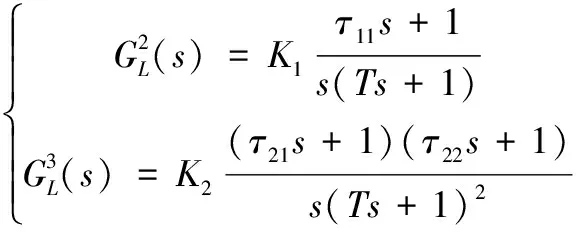
(7)
其中:
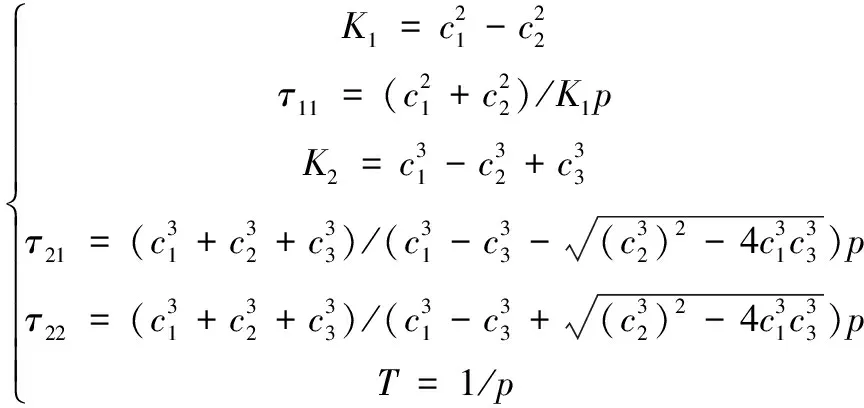
基于式(6)和式(7)的控制器模型,可计算出PID控制器和拟拉盖尔控制器的频域增益:
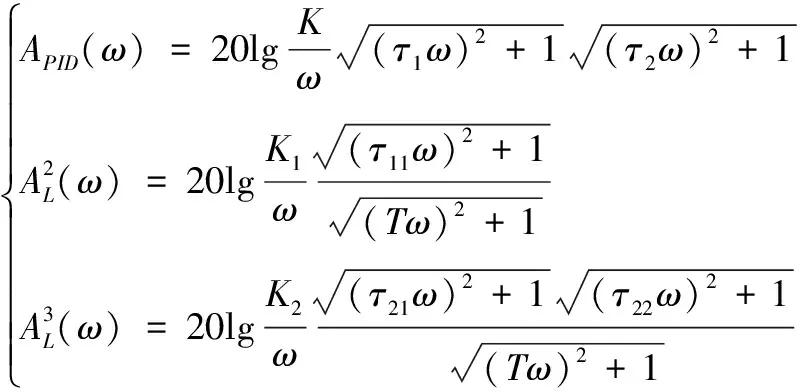
其幅频渐近特性如图2所示。
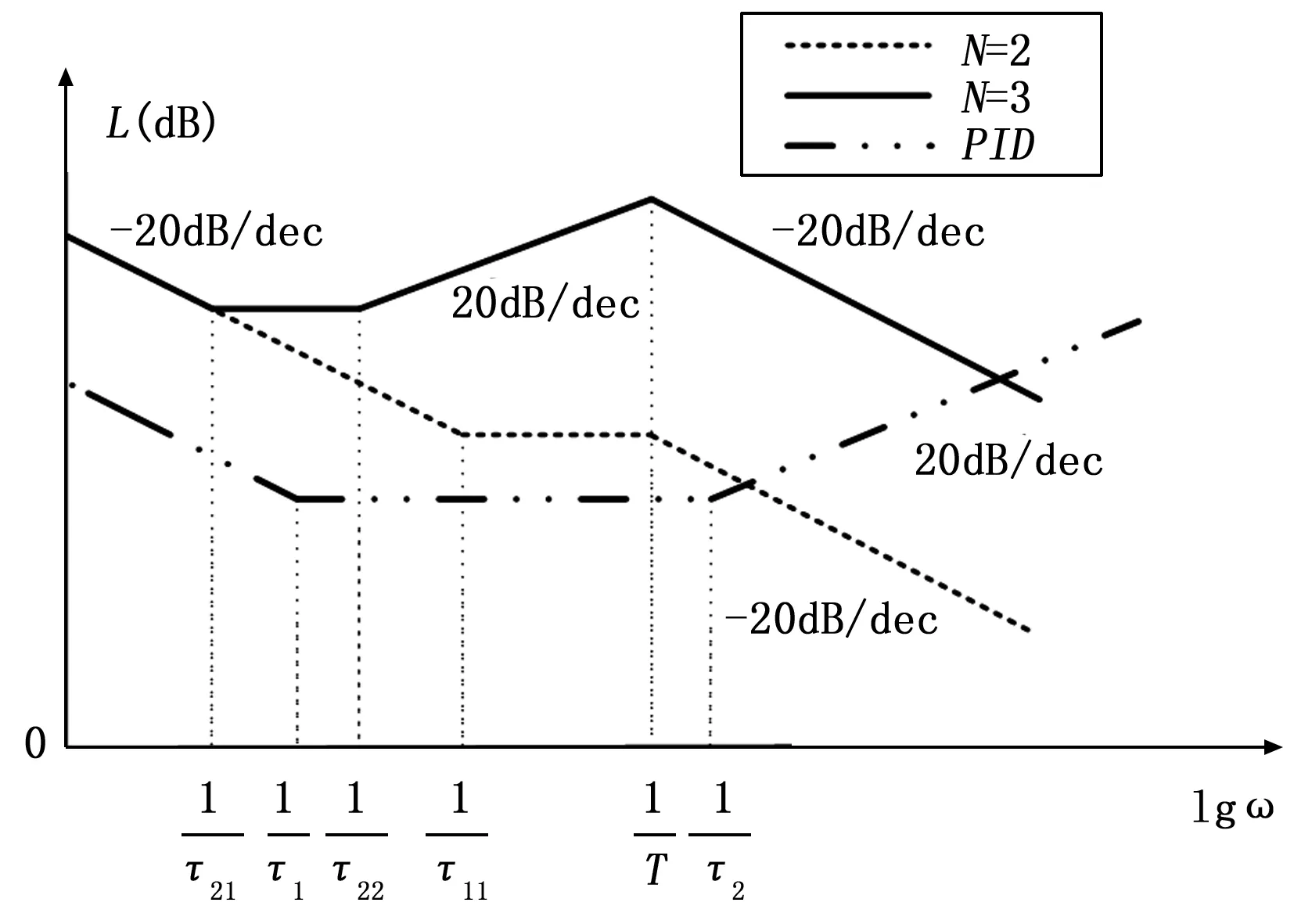
图2 PID控制器和拟拉盖尔控制器幅频渐近特性
从低频增益特性上看,两种控制器模型都具有无穷大的低频增益和-20 (dB/dec)的低频斜率,可以实现位移无静差控制。但二者的高频增益却相差很大:
PID控制器增益随着频率的升高而趋近于无穷大,拟拉盖尔控制器随着频率的升高而趋近于无穷小。由于干扰信号一般具有较高的频率成分,从抗干扰角度考虑,控制器高频增益过大,不利于抑制高频干扰。因此,从幅频特性上看,拟拉盖尔控制器理论上比PID控制器具有更好的高频抗扰性能。
两种控制器的相频特性如式(8)所示:

(8)
在ω((0,+∞)的频段,PID控制器的相角范围为:
θPID(ω)(-0.5π,0.5π)


4 拟拉盖尔控制器参数整定
基于性能指标的设计方法,是控制系统的一种常见设计方法,这类方法可以让待设计的控制系统逼近期望的系统性能。
期望的系统性能,可以是时域的调节时间和超调量[19],也可以是频域增益[20]或稳定裕度[21],还可以是综合反映时域和频域性能的期望模型[22]。本文基于模型逼近技术[22-24],分别给出PID控制器的参数整定公式和拟拉盖尔控制器参数的整定公式,便于在相同设计方法下,比较两种控制器的不同性能。
设如图3所示典型结构的控制系统中,Gc(s)是控制器模型,Gp(s)为被控对象模型,R(s)、D(s)和Y(s)分别为系统输入、扰动输入和系统输出。
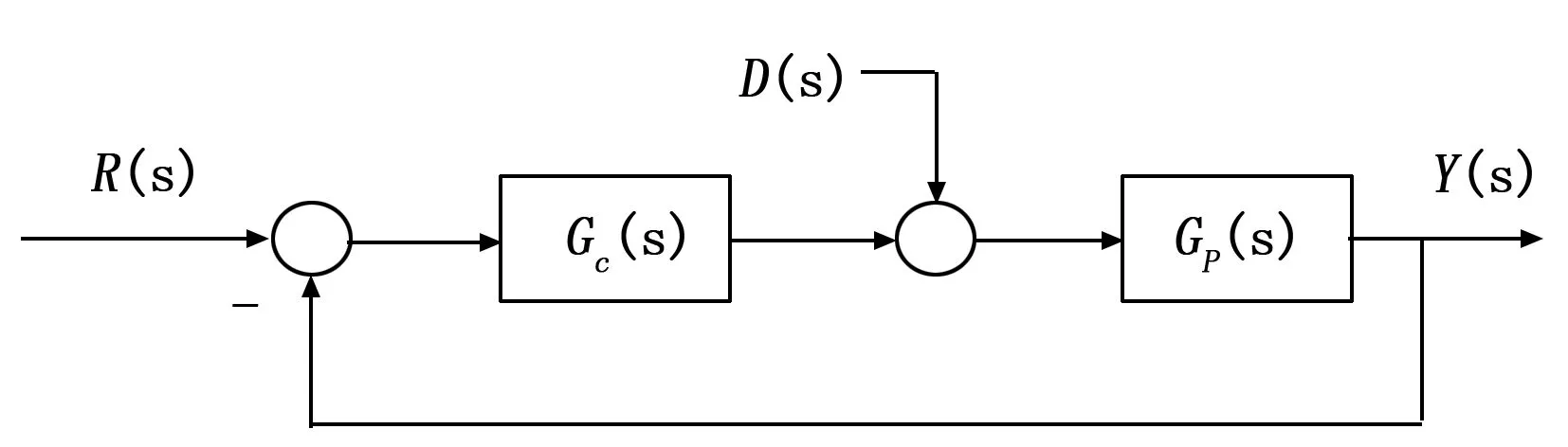
图3 控制系统典型结构图
根据如图所示系统结构,可以得到闭环系统的数学模型:
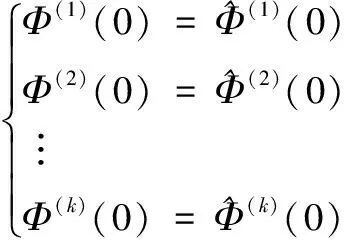
(9)
便可利用前k个等式关系,推导k个控制器参数的计算公式。
对于式(6)所示PID控制器,按照式(9)所示等式条件,将前三项方程联立求解,可得到Kp、Ki、Kd的整定公式:
(10)

基于上述处理思想,二阶拟拉盖尔控制器参数表达式为:

(11)
三阶拟拉盖尔控制器参数表达式如下:
设置参数初始值,包括种群规模ps、遗传算法最大容忍停滞代数G1、模拟退火操作Markov链长度LM等,并令当前代数ge等各计数器的初始值为0。
(12)
其中:
由于式(11)和(12)未给出参数p的选择原则,导致p为一自由参数。文献[25]表明,在大多数情况下,参数p对系统性能影响不大,一般情况下可以根据先验知识预设一个固定值,并建议取p=25。
5 仿真研究
为了研究拟拉盖尔控制器的跟踪性能和抗干扰性能,并与PID控制器进行比较,本文选择三类不同的被控对象(低阶时滞对象、高阶无时滞对象以及非最小相位对象):
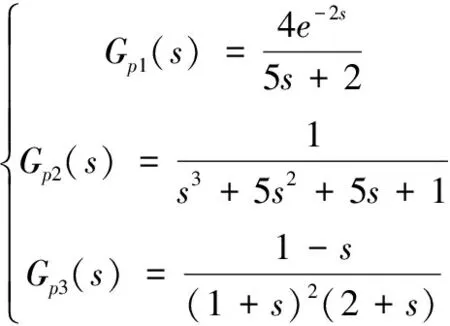
这三类被控对象所对应的期望系统分别设置为:
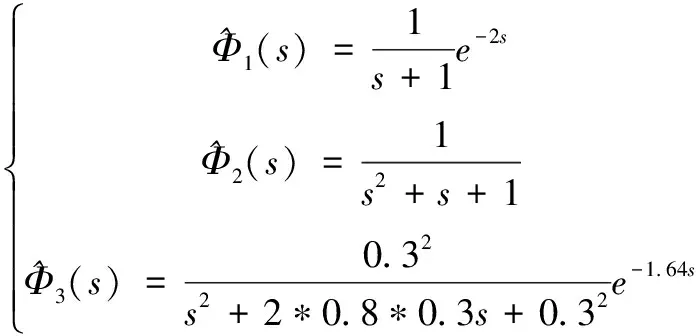
5.1 逼近度比较
本节主要考察在阶跃信号作用下,拟拉盖尔控制系统与PID控制系统对期望系统的逼近能力。
对于低阶时滞对象Gp1(s),利用公式(10)~(12),计算可得三个控制器参数如下所示:

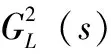

图4 参数p对系统逼近度的影响
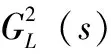
为了能量化系统逼近度,将控制系统与期望系统时域响应的偏差绝对值进行积分(IAE),作为控制系统逼近度的衡量指标:
(13)
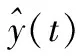
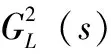
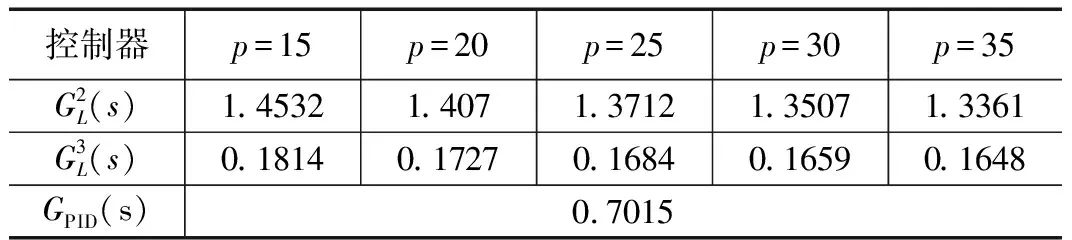
表1 拟拉盖尔控制器与PID控制器的逼近度比较

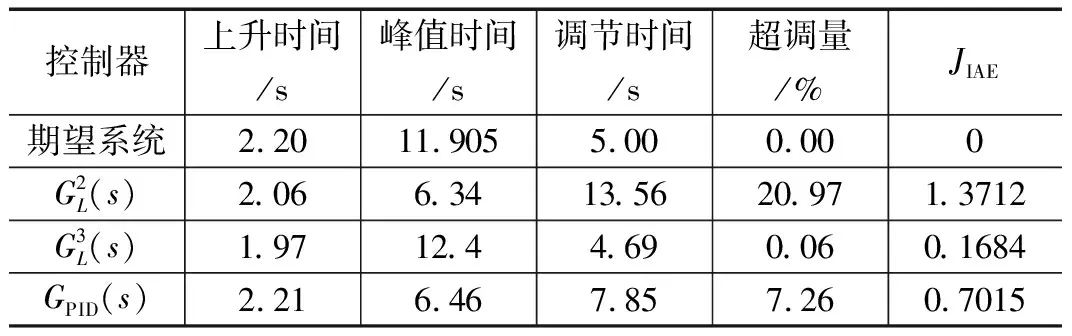
表2 拟拉盖尔控制器与PID控制器的综合性能比较
对于高阶无时滞对象Gp2(s),利用公式(10)~(12)计算得到的三种控制器参数(p=25)如下:

图5为三种控制系统在阶跃响应作用下的曲线,三者的区别十分明显。
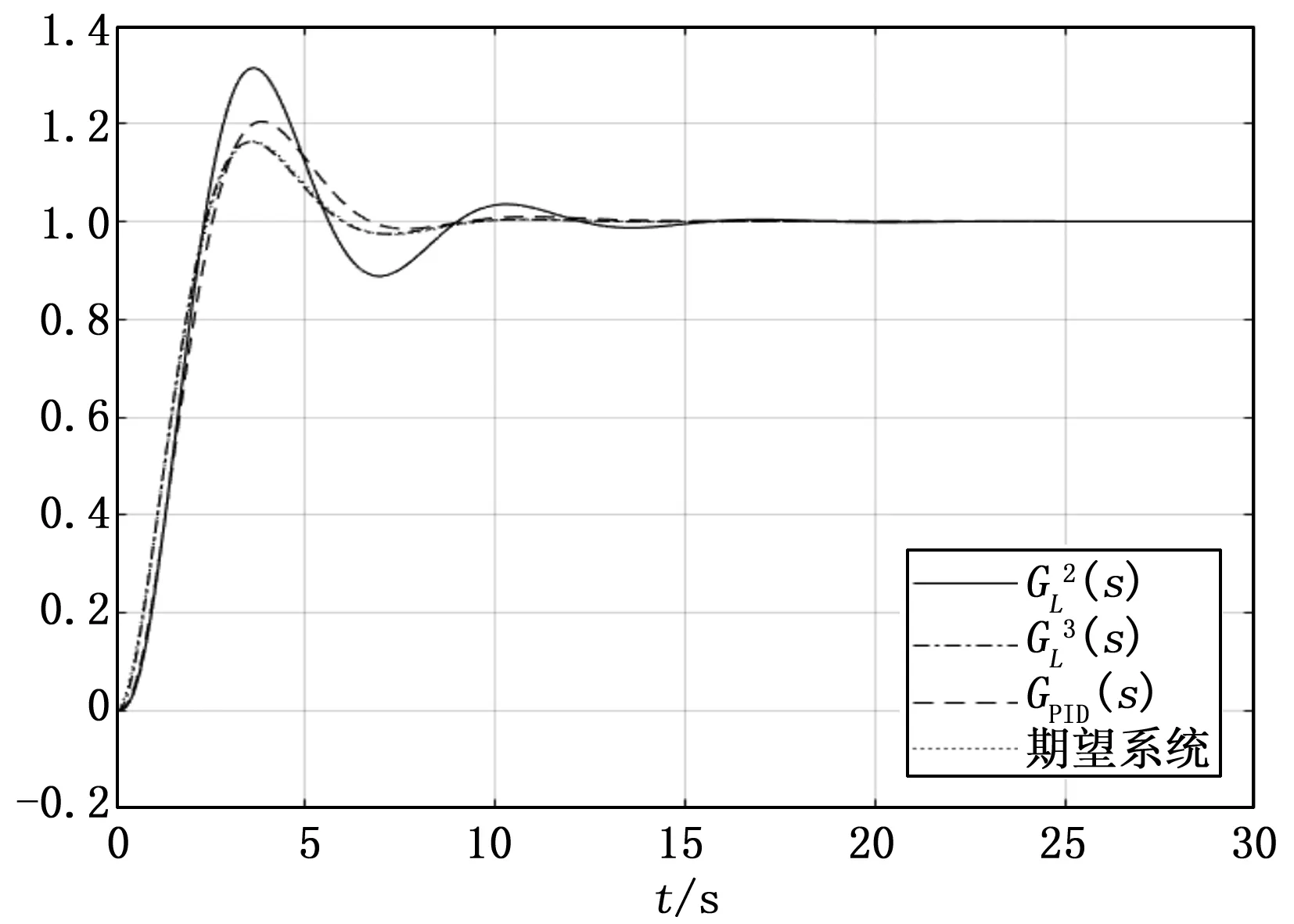
图5 高阶无时滞系统阶跃响应
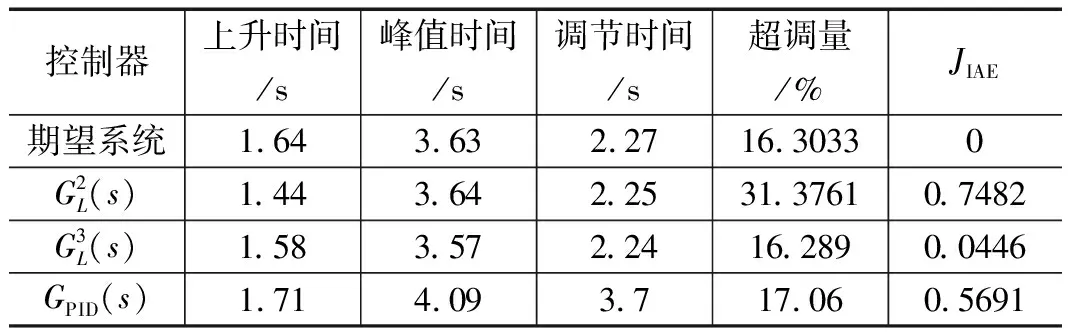
表3 拟拉盖尔控制器与PID控制器的综合性能比较
采用上述同样的方法,得到非最小相位对象Gp3(s)的三种控制器参数(p=25)如下:
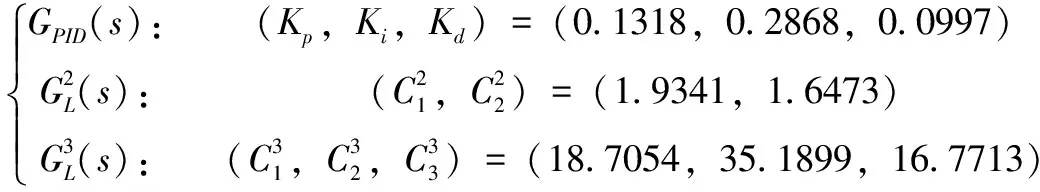

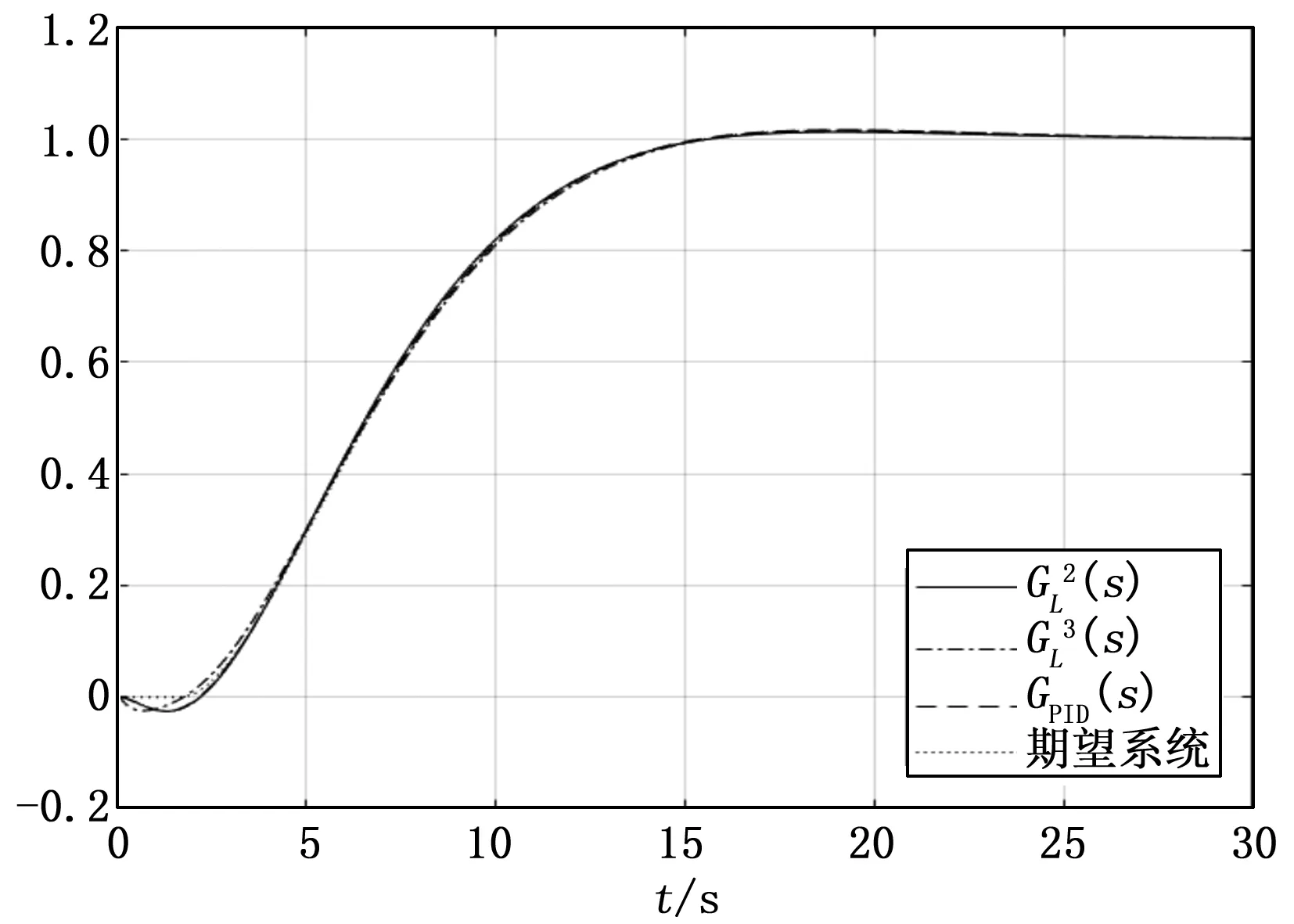
图6 非最小相位系统阶跃响应
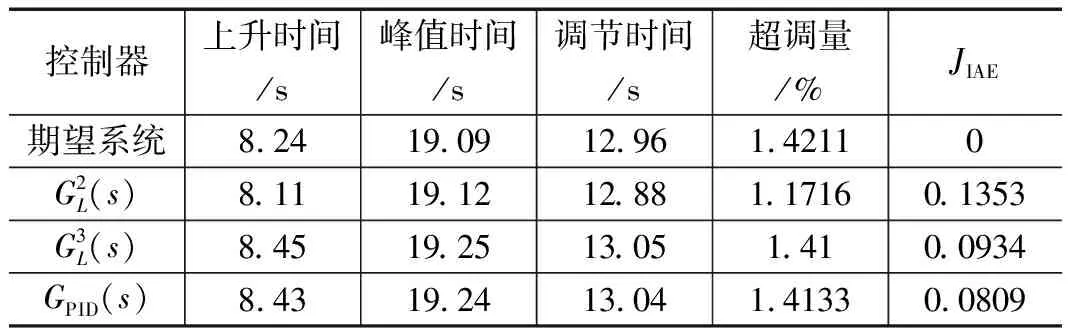
表4 拟拉盖尔控制器与PID控制器综合性能比较
上面三例分别给出了三种控制器在三类不同类型被控对象上的控制效果及其与期望系统阶跃响应的差别。为了能对三种控制器的逼近性能综合排序,将三种控制器在三类被控对象上逼近能力的独立排序结果列入表5中,然后计算各自排序均值,作为三种控制器逼近能力的得分。分值越小,逼近能力越强。
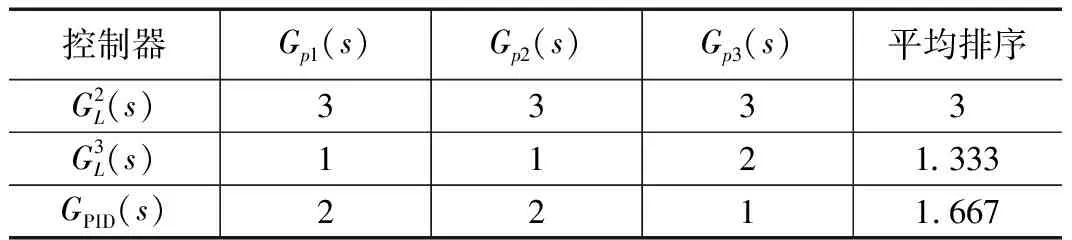
表5 拟拉盖尔控制器和PID控制器逼近度排序
5.2 抗扰性能比较
控制系统在实际工作的过程中,不可避免地会受到外部信号的干扰,例如风对悬吊物的随机影响、牵引过程中的负载突加和突减等。本文仅研究单位阶跃干扰为D(t)=1(t)和正弦干扰D(t)=sin(2 000πt)时,三种控制系统对干扰的抑制能力。
为了能量化系统的抗扰性能,仍采用IAE指标作为评价标准。

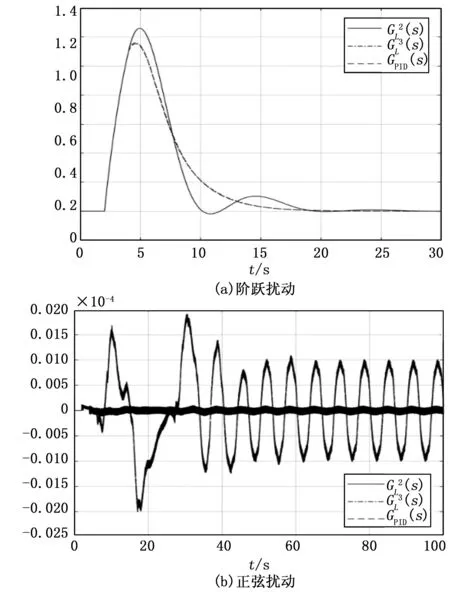
图7 时滞对象Gp1(s)的扰动响应

表6 抗扰性能JIAE
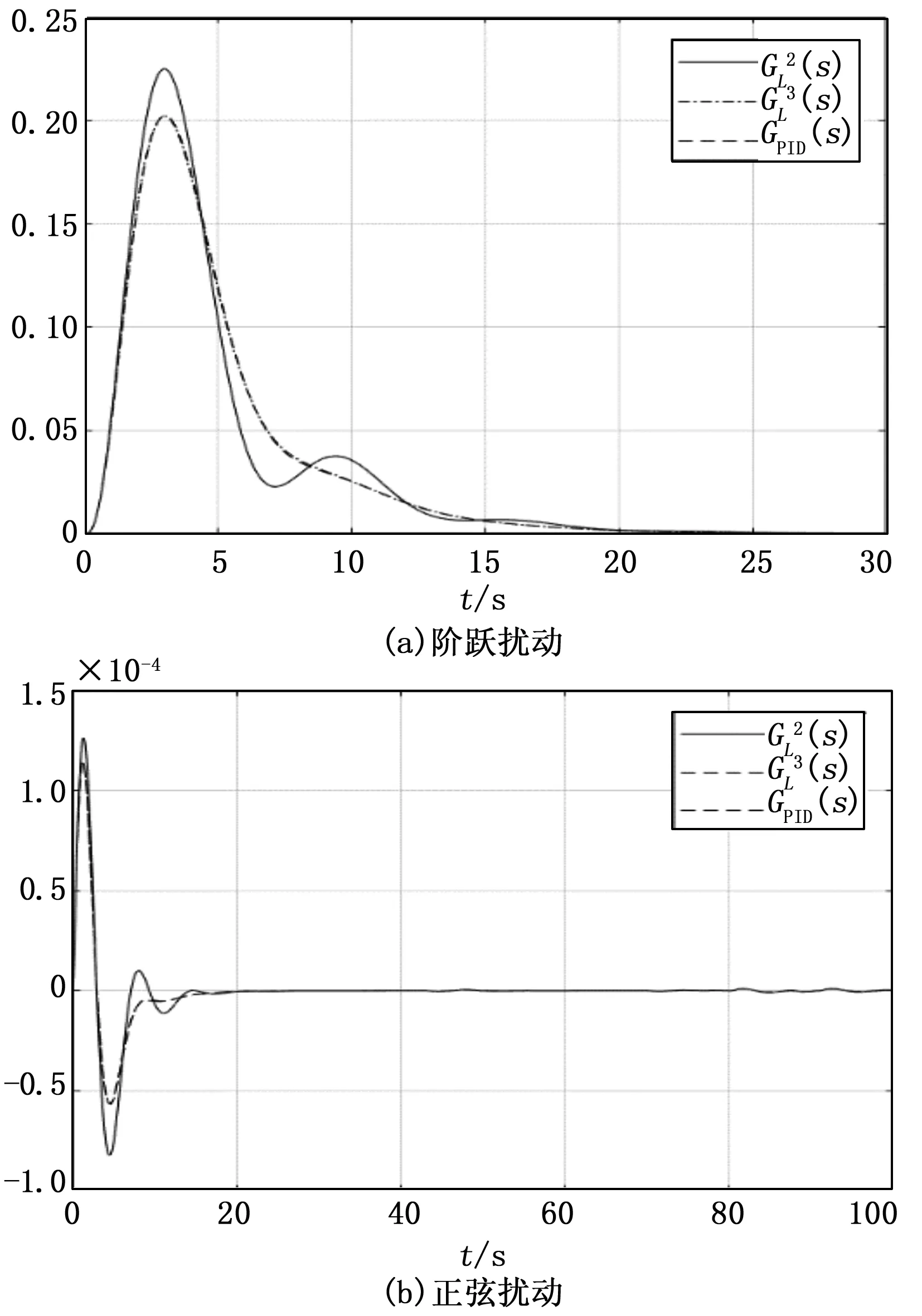
图8 高阶无时滞对象Gp2(s)的扰动响应

表7 抗扰性能IAE
图9是非最小相位对象Gp3(s)的扰动响应过程,扰动响应曲线难以分辨。
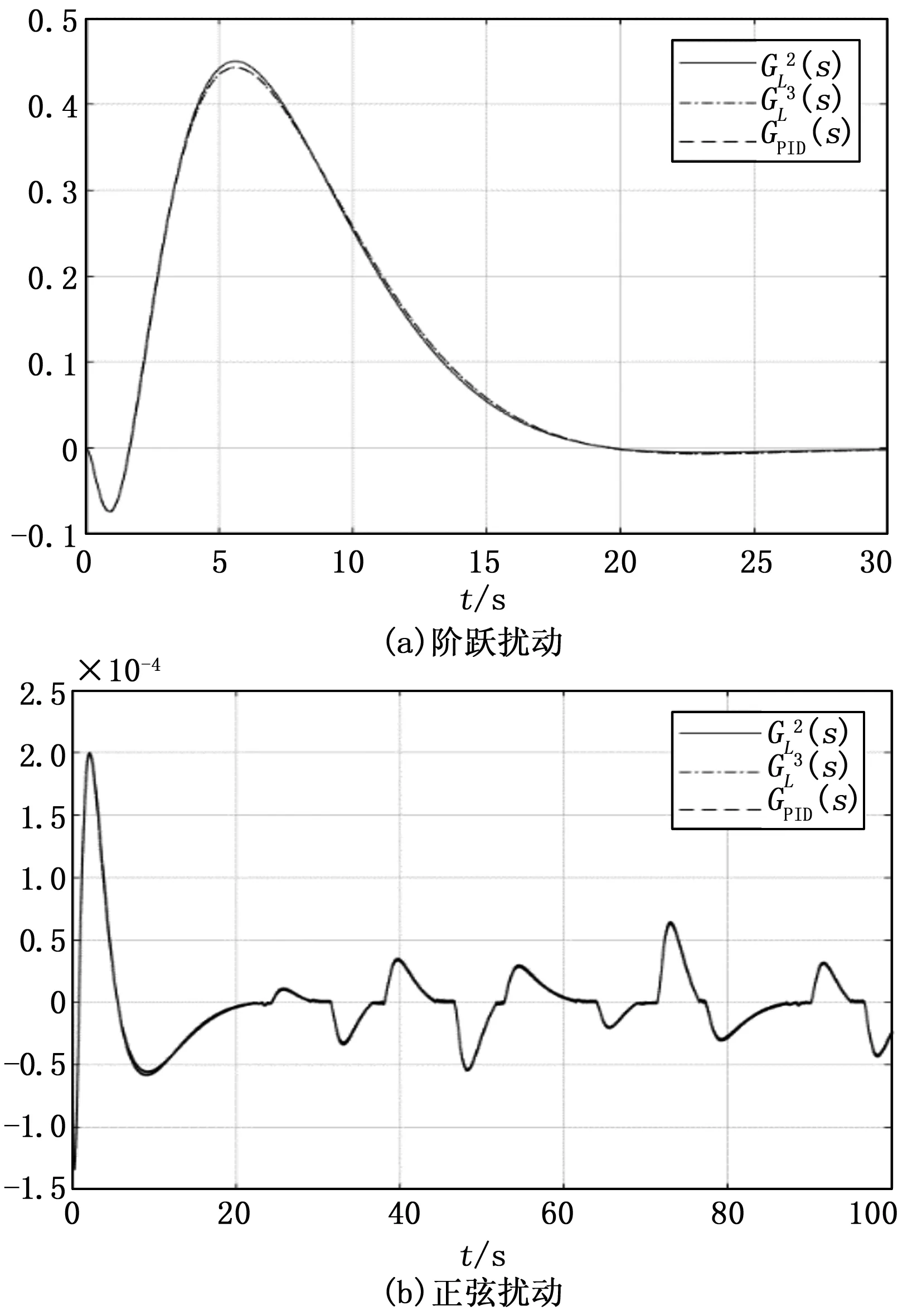
图9 非最小相位对象Gp3(s)的扰动响应

表8 抗扰性能IAE

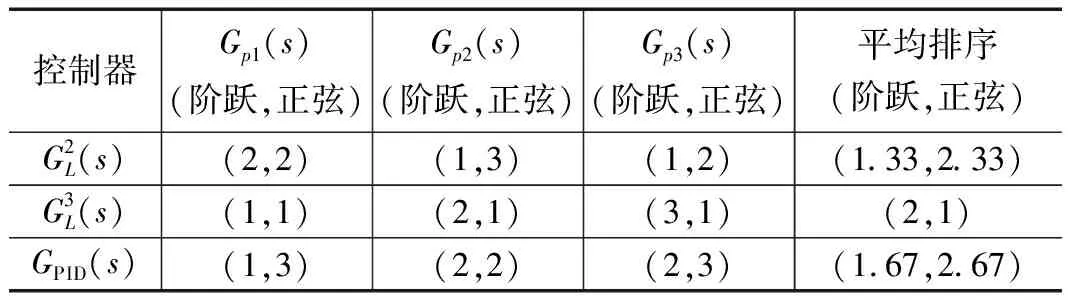
表9 拟拉盖尔控制器和PID控制器抗扰性能排序
GPID控制器得分2.17。这意味着,在三类被控对象的扰动实验中,PID控制器的抗扰性能不如拟拉盖尔控制器。这正如前文频域特性分析那样,高频增益过高,不利于抑制扰动对系统带来的影响。仿真实验的结果与前文频域理论分析相符。
6 结束语
本文利用连续拉盖尔级数,设计了一种拟拉盖尔级数型连续控制器模型,并基于模型逼近技术,采用麦克劳林展开获得求解条件,给出了拟拉盖尔控制器和PID控制器的参数整定公式。在相同设计方法前提下,通过三类被控对象的仿真实验,对拟拉盖尔控制器和PID的逼近度和抗扰性能进行了比较研究。