船载S频段测控系统全频段校相方法研究
2021-12-01石启亮曾俊康王鑫奎
石启亮,曾俊康,王鑫奎
(中国卫星海上测控部,江苏 江阴 214431 )
0 引言
航天测量船S频段测控系统跟踪接收机采用双通道单脉冲跟踪体制[1],该体制存在和、差通道的相位不一致会影响系统跟踪性能的问题[2],因此测量船在出海前需要预先针对航天器对应工作频点、极化方式、设备组合进行校相,保持和、差信道相位一致性,才能确保测控系统稳定跟踪。测量船传统校相方法是采用码头对塔校相+微波自检即无塔标校技术[3-4]的方式,即在码头时对塔校相逐个获取所需相位值,海上则采用微波自检,以及施放信标球等方式修正相位漂移,取得了很好的效果[5-6],后来又发展应用了快速校相技术[7-9],但这些方法仅适合于跟踪设备工作相对稳定、相位漂移不大、工作频点数量有限的条件下使用。由于测量船工作环境的特殊性,面临两方面的问题:一是在出海期间工作通道器件出现故障进行更换后,原对塔相位将无法使用,需要重新施放信标球进行标定,但只适合于有限个频点校相,而动态对星校相又很难有相同点频的卫星且校相精度较低;二是随着需要跟踪测量的航天器数量的增多,尤其是对未知频点的航天器的试验性跟踪,无法在出海前完成覆盖所需频点的对塔校相工作。因此提出一种基于数据分析的校相方法,通过对有限数量频点的校相数据的分析计算,确定校相公式,实现覆盖整个工作频段的校相工作。
1 角跟踪原理分析
双通道单脉冲跟踪体制利用和、差模信号的特性实现对卫星目标的稳定跟踪,目标信号经天线反射面后进入馈源网络形成和、差信号,送至跟踪接收机解调方位、俯仰角误差电压,并驱动天线对准目标[10-11]。角误差信号产生原理如图1所示。
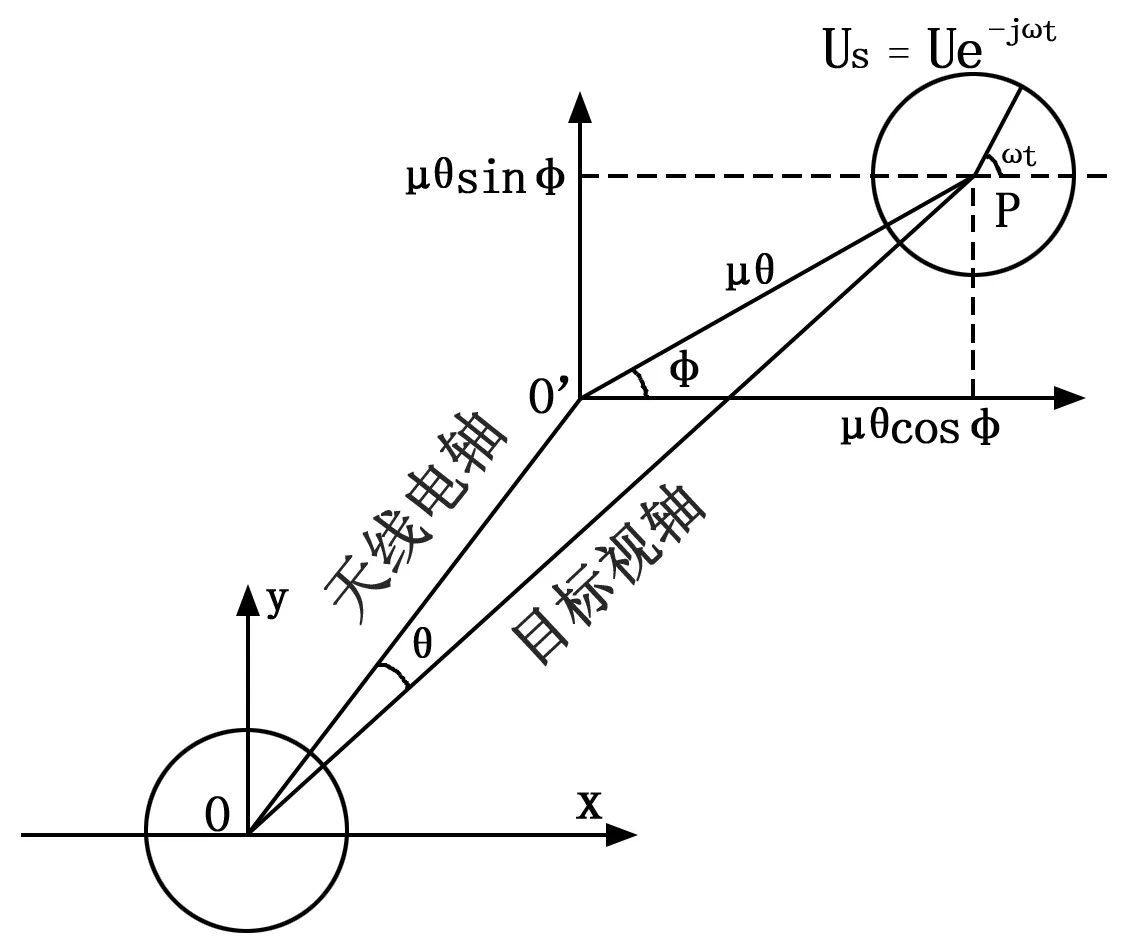
图1 角跟踪信号形成原理
当天线电轴偏离目标P指向一个小角度θ时,则馈源口输出和、差信号可表示为:
uΣ(t)=Ucos(ωt)
(1)
uΔ(t)=μθUsin(ωt+φ)=
μθUsinφcosωt+μθUcosφsinωt
(2)
式中,μ为差方向图归一化斜率;φ为天线电轴与目标P构成的平面与水平面的夹角;U为信号强度[6]。
以左旋信号为例,跟踪解调后的角误差电压为:
(4)
(5)
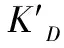
当φ1-φ2≠0°或φ1-φ2≠180°时,方位、俯仰角误差会产生交叉耦合,交叉耦合等于相位差φ1-φ2的正切[12]。跟踪接收机校相的目的是获得跟踪链路和、差通道之间的相位差Δφ并进行补偿消弭。由于角跟踪设计中,校相时天线先对准目标即找准零点后,天线一个支路(如方位)正向拉偏时出负电压,而另一支路为0。综合基带进行角跟踪解调时,在和支路增加一个可调移相器,相位调整值为Δφ,并满足(φ1+Δφ)-φ2=180°,那么Δφ可表示为:
Δφ=-(φ1-φ2)+180°+n×360°
(6)
式中,n为确保Δφ在0~360°之间的整数。
2 基于数据分析的校相计算方法
2.1 和、差通道相位差分析
信号经天线接收后在馈源网络中激励出和、差信号,依次经过低噪声放大器LNA、下变频D/C、中频电平调节、中频矩阵等设备后,经综合基带和、差信号归一化处理、跟踪解调、窄带低通滤波后得到角误差信号[13]。
由于和、差信号经过的物理路径不同(波导、连接电缆长度不同以及链路设备器件间存在的差异),导致综合基带角误差解调时和、差信号之间存在相位差[14]。从和、差信号接收开始至角误差解调输出,测控系统内部产生的和、差通道相位差可以分成三段:经馈源网络、场放LNA至下变频器D/C之间的射频段相位差φ射频;和、差通道下变频器至综合基带输入口端之间引入的中频段相位差φ中频;综合基带内部信号传输、采样、解调处理引入的相位差φ基带。另外对塔校相时,还需考虑外界到天线面馈源口和、差信号相位差(近场效应)φ近场。那么在近场对塔校相获取和、差通道相位差时,总相位差可表示为:
φ1-φ2=φ射频+φ中频+φ基带+φ近场
(7)
由式(6)、(7)可得:
φ射频+φ中频+φ基带+φ近场=
-Δφ+180°+k×360°
(8)
可以通过构建中频闭环校相校相,分别计算得到φ中频、φ基带值。对同一设备组合、综合基带工作模式而言,由于系统中频段频率较低、波长较长,除非和、差通道连接线缆、设备插箱或器件故障,否则受外界条件影响较小,正常工作状态下其漂移可以忽略,因此φ中频、φ基带基本为固定值,不受射频工作点频切换的影响。
2.2 近场效应分析
受经济、环境等条件限制,建立的标校塔难以满足远场条件,因此测量船采用近场法进行角度标校。由于接收天线对标校天线辐射场存在近场效应,导致接收天线馈源口和、差信号出现附加相位差[15-16],而跟踪卫星时则为远场条件,额外附加相位差很小,可以忽略不计,对塔校相获取的相位值与实际跟星相位存在一定的偏差。因此在进行校相参数分析计算时,首先要剔除近场效应引入的附加相位差φ近场。依据文献[15],采用近场感应解析法[17]对接收天线的近场方向图进行仿真分析,船载S频段测控系统采用12米口径天线,在频点为2 250 MHz时,和、差信号相对相位与距离的关系仿真曲线如图2所示,图中R为塔距,R0= 2D2/λ为满足远场条件的距离[18-19]。

图2 天线和差口相对相位差与距离的关系
和、差通道真实的相位差应为测控系统对塔校相获得的相位值减去近场效应引入的相位差φ近场。测量船标校塔塔距R为980 m,约为远场距离的1/2,天线和差口相对相位差与频点的关系如图3所示。
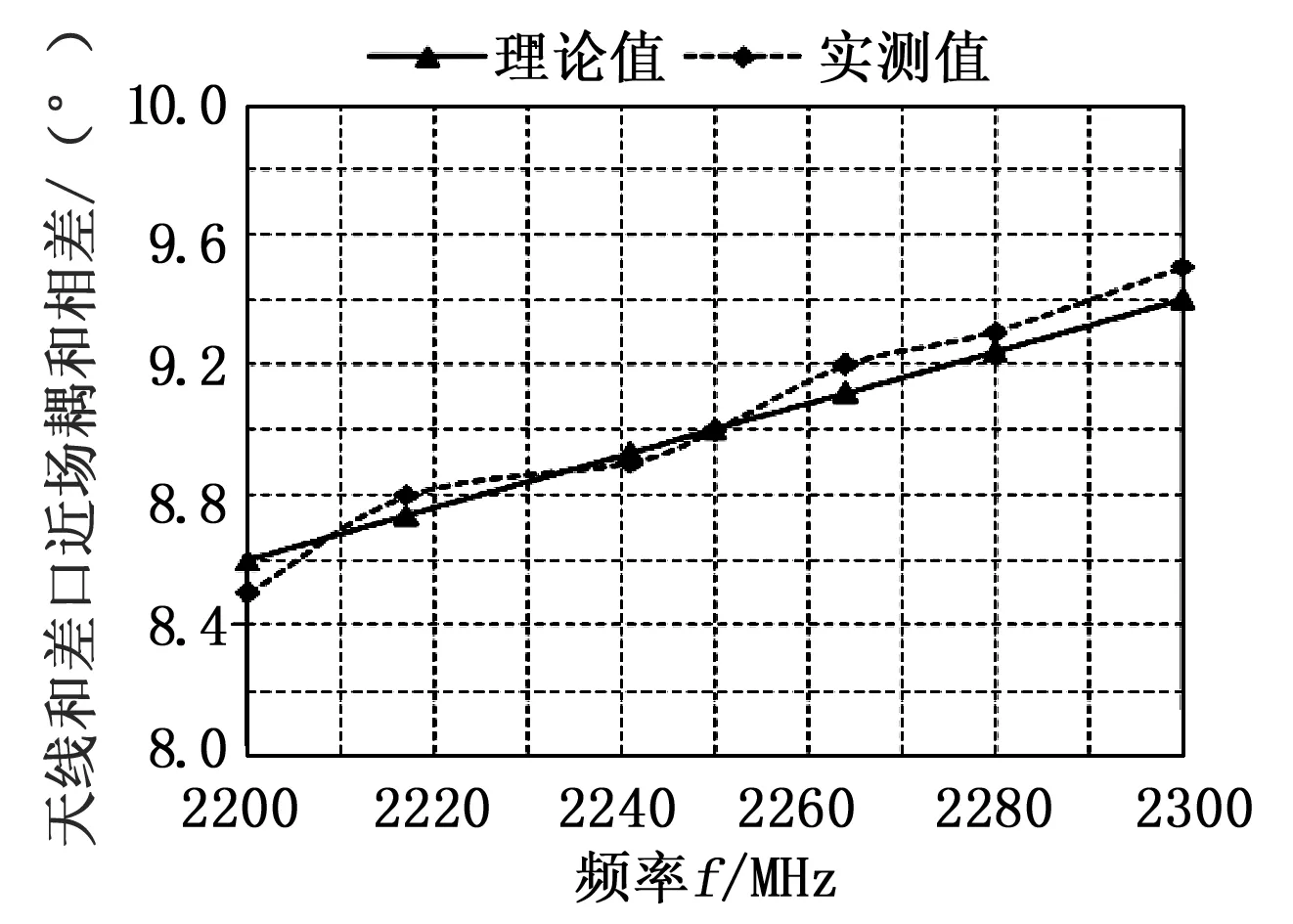
图3 天线和差口相对相位差与频点的关系
由于相位测量误差的存在,对星/对塔相位差实测值与理论仿真值基本相符,且在100 MHz带宽内两者相差约为9±0.5°,是以在校相参数计算时可以将相位差修正值统一取φ近场=9°。在实际应用中,可以按照该方法进行相位修正,即在对塔校相获取的相位值上减去9°后作为实际跟星相位。因φ近场变化量较小,结合分析由式(8)可知Δφ变化量近似等于φ射频变化量。
2.3 校相估算方法分析
对于两个不同频点f1、f2(对应波长为λ1、λ2)而言,两者之间的相位偏移量Δφ′可表示为[20]:
Δφ′=360°|(L1-L2)/λ1-(L1-L2)/λ2|
(11)
式中,L1,L2是和、差通道射频段的物理路径长度,记ΔL=L1-L2,那么ΔL>0时表示和通道物理长度大于差通道,反之ΔL<0时表示和通道物理长度小于差通道。
从式(11)可知,若和、差通道物理路径长度保持不变,即在相同工作条件下进行不同频点的对塔校相时,随着工作频点的变化,将产生相位偏差。而在工作频点一致时,若存在外界干扰的、电缆松动等影响,则和、差通道波程差发生变化,也会产生相位偏差。因而不同工作频点对塔校相时必须在相同工作状态和环境条件下开展。
若设备工作状态一致,在频点f1保持不变,而f2发生变化的情况下,公式(9)可转化为:
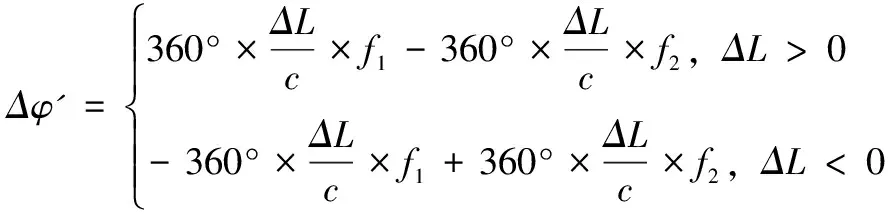
(12)
由上式可知,在同一校相条件下Δφ′为随f2变化的一次曲线。
在S频段100 MHz工作带宽内,若相位差最大变化为一个周期(360°)时,则根据式(12)计算可得和、差通道物理长度绝对值ΔL≈3 m。若ΔL>3 m,和、差通道相位差变化将超过一个周期。通过仿真计算,对应不同ΔL,相位差和频率之间的变化关系分别如图4(a)、(b)所示,相位差在一定频率周期内呈周期性0~360°线性变化。ΔL>0时,相位差随工作频率增大而变大,斜率为正;ΔL<0时,相位差随工作频率增大而变小,斜率为负。
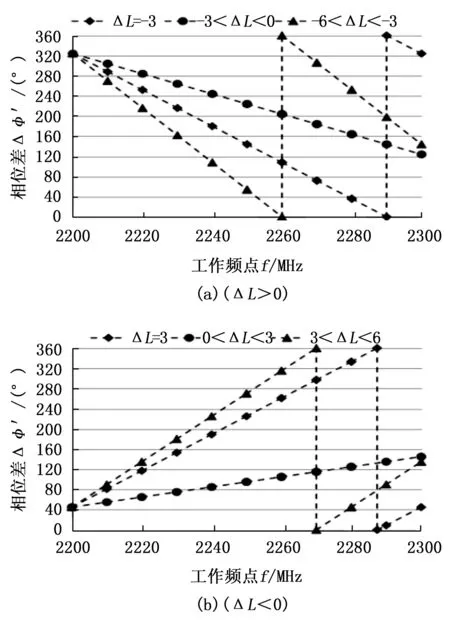
图4 相位差和频率变化示意图
通过更改设备配置、线缆短接等方式,分别构建射频有线回路和中频回路。利用综合基带测距功能对左旋和、左旋差、右旋和、右旋差4个通道进行距离测量,可以粗略得出左旋和、差通道射频段距离差约为0.757 m,右旋距离差约为0.136 m,由于综合基带采用单程测距方式,因此实际下行接收左、右旋和、差通道射频段物理长度差分别约为1.514 m、0.272 m,绝对值均小于3 m,因此在工作频带内左、右旋和差通道相位差变化不超过一个周期(360°)。
对任一点频f,和、差通道射频段物理长度差ΔL可表示为:
(13)
式中,λ为波长,N为波长的整数倍;K=λ×Δφ/360°为余量。结合式(8),Δφ即为φ射频,即对塔校相值扣除φ中频、φ基带并经近场效应修正后的相位值。当ΔL>0时,N>0,反之ΔL<0时,N<0。对于同一设备组合、工作状态、同一基带工作模式下而言,ΔL保持不变,那么任意两个点频f1、f2,可得到:
(14)
N1=N2+ΔN
(15)
在ΔL未知的情况下,那么两个相近频点f1、f2对应包含的整数倍波长相同,即N1=N2,而当两个工作点频f1、f2间隔较大时,可能会出现两个频点对应包含的整数倍波长不一致的情况,此时ΔN=|N1-N2|为大于零的正整数,因此需要通过结合和、差通道长度判断计算ΔN值。从前文分析已知在S频段工作带宽为100 MHz内,需|ΔL|>3 m时才会出现和、差通道相位差变化超过一个周期的情况,而实际左、右旋和、差通道之间均满足|ΔL|<3 m,因此ΔN=0,此时式(13)可转换为:
(16)
2.4 基于对塔校相数据推导的相位公式
通过更改设备配置、线缆短接等方式构建中频闭环回路,需确保和、差通道短接线电长度基本一致,若不一致需通过仪器测量加以修正,避免引入额外偏差。利用综合基带校相功能进行中频校相,根据式(9)、式(10)计算得φ中频、φ基带值,实测结果见表1。

表1 中频相位修正值
在下行信号S频段100 MHz工作带宽内每隔10 MHz进行一次对塔校相,并对其结果进行拟合修正。考虑到校相误差的存在,首先根据前文分析对校相数据进行直线拟合处理粗略修正校相误差,然后进行近场效应修正并减去φ中频、φ基带值,计算得左旋N=11.997,详细数据见表2。
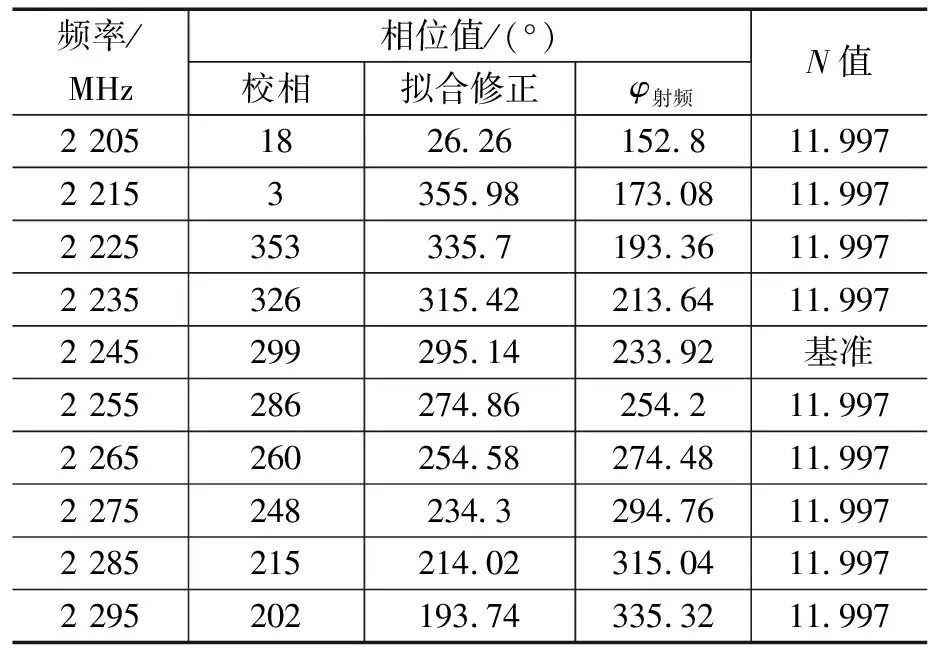
表2 左旋对塔校相数据分析计算
取整后令左旋N=12,那么可以确定左旋和、差通道射频段物理长度差|ΔL|≈1.56 m。根据式(8)、(16),左旋射频段相位差计算公式如下:
Δφ射频=(360°×N+180°-φ0-10.94°)/f0×f+
n×360°
(17)
式中,f为工作频段内任意点频,φ0为已知点频f0对应相位。
经过采用相同方法对右旋和、差通道相位差进行分析计算,得到右旋N=2。根据式(8)、(17)可得左、右旋相位差Δφ计算公式如下:
Δφ=k×f+φ0+n×360°
(18)
式中,左旋时k=-2.028 480,φ0=169.06°;右旋时k=-0.322 667,φ0=170.45°。系统其他链路的k、φ0采用相同方式计算获取。
2.5 实验结果验证分析
在工作带宽内,根据实际卫星点频,按式(18)分别计算左、右旋和、差通道相位值,与对塔校相获取并经过跟星修正的各点频相位值偏差见图5。

图5 理论计算和对塔相位值偏差关系
船载测控系统稳定跟踪目标,要求跟踪接收机交叉耦合小于1/5[12],按左旋公式推导计算的相位值与实际跟星所需相位值最大偏差为8°,而右旋推导计算的最大偏差为7°,均满足该要求。采用相位公式计算的几组对应相位值进行跟星验证,跟踪线性良好,交叉耦合较小,充分验证该方法有效,因此采用该方法归纳总结出海上标校新方法。
3 海上相位标校新方法
3.1 相位修正/标校方法
基于上述分析,在出海以后,对已知卫星工作点频f0进行跟星时,若检测到交叉耦合恶化,和、差通道相位差发生漂移Δφ0,此时相位为φ0+Δφ0,需要对相位计算公式(18)中k、φ0进行修正,修正后k为:
(19)
若设备故障更换器件时,由于无法对塔校相,可以通过选择若干已知频点、角速度不大的高轨目标,采用对星校相的方法获取一组相位值再进行相位公式推导,海上动态情况下校相误差较大,优点是无需考虑近场效应的影响。为了修正校相误差,以及避免在ΔL未知时出现相位差变化超过360°的情况,至少采用4~5个点频的校相值进行拟合,并从拟合相位曲线斜率确定ΔL的范围,再精确计算出N值后,最终推导出整个工作频段左、右旋相位公式。
3.2 不同工作模式相位修正方法
S频段综合基带中有多种工作模式,通过加载不同的程序来实现模式之间的切换,在设备组合相同的情况下,即和、差通道保持一致,那么相位值的不同是由于基带不同工作模式解调处理程序的不同导致的,因此可以在已知工作模式相位值的基础上提供修正得到另一种工作模式的相位。设两个基带工作模式之间相差为Δφ基带,首先通过基带自闭环校相获取两个工作模式之间的相差Δφ基带,然后将式(19)中Δφ0替换为Δφ基带后对斜率和初始相位进行修正即可。
3.3 在单通道单脉冲体制中的应用
测量船中还存在着单通道单脉冲跟踪体制,在该体制中,和、差信号经LNA放大后,在和差网络中合成单通道信号进行传输,因此不需要考虑中频传输段带来的和差信号相位差,在利用该方法估算时只需令φ中频=0、φ基带=0即可进行估算,该方法不仅可以获取全频段相位,还可以反应馈源网络中和、差通道物理路径差异。
4 结束语
通过分析双通道单脉冲体制跟踪原理,和、差通道相位差的组成,仿真计算确定和、差通道物理路径长度差值与相位差之间关系。由于对塔校相数据是处于静态条件下获取的相位值,准确性较高,因此在剔除近场效应的影响后,基于测控系统各设备组合的对塔校相数据进行校相参数计算,获取相关参数后得出相位差计算公式。在此基础上归纳总结出海上相位修正及标校方法和基带不同工作模式之间相位修正方法,通过编写相应的功能软件准确快速计算任一点频的相位值及修正,实现测量船S频段测控系统全频段海上相位标校工作。
