基于迭代学习控制的PMSM周期性转矩脉动抑制*
2021-12-01季鹏鹏
季鹏鹏 潘 丰
(江南大学轻工过程先进控制教育部重点实验室 无锡 214122)
1 引言
永磁同步电机(Permanent Magent Synchronous Motor,PMSM)性能优越,广泛用于各个领域,逐渐成为高精度伺服控制系统执行电机的主流[1]。但在实际工作环境下,受逆变器固有非线性特性和气隙谐波磁通等因素影响,使电流发生畸变并引起电机产生周期性转矩脉动。转矩脉动的存在影响了系统的精确定位性能。因此,永磁同步电机转矩脉动的抑制成为国内外学者研究的热点。
针对永磁同步电机转矩脉动抑制,从电机的控制策略出发,通过选择和结合近几年提出的各种智能算法,补偿电机控制电流或电压,从而抑制转矩脉动。常见的方法有谐波电压注入[2]、比例积分-准谐振补偿器[3]、死区前馈补偿[4]等。近年来迭代学习控制算法(Iterative Learning Controller,ILC)在永磁同步电机上得到了广泛应用,文献[5]提出了一种基于迭代学习控制算法的转矩脉动抑制策略,该方法将负载转矩与电机输出转矩的偏差信号经在线迭代学习补偿到q轴电流的给定端,实现转矩脉动抑制,效果良好。文献[6]针对转速纹波引起的周期性转矩脉动,提出了一种基于开闭环P型迭代学习控制算法替代转速调节器,也取得了较好的效果。此外,人工神经网络、扩展卡尔曼滤波、模糊控制等也被运用到转矩脉动抑制中[7~9],但这些方法较为复杂,在实际工程中实用性不强。
针对PMSM周期性转矩脉动,提出一种基于迭代学习控制的转矩脉动抑制方法,将转速环的输出与系统输出转矩的实时误差经迭代学习补偿到q轴电流给定,同时利用改进的粒子群算法(Particle Swarm Optimization,PSO)对迭代学习控制器中的关键参数进行优化整定,提高转矩脉动抑制效果,并对提出的方法在仿真平台进行验证,同时与文献[5]和文献[6]中的方法进行对比分析,从而验证本文方法的有效性。
2 永磁同步电机数学模型
以面装式永磁同步电机为被控对象,考虑到实际运行状态下的气隙磁变、逆变器管压降和死区时间等因素,导致电机三相电压产生畸变,包含5、7、11、13等一系列高次谐波,其中5、7次谐波对系统影响较大,因此PMSM谐波模型为
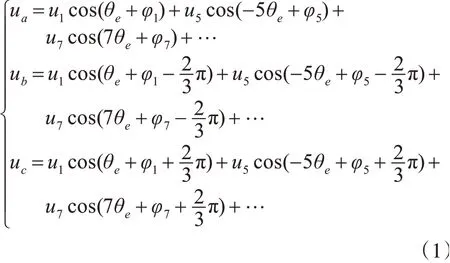
其中,θe为电机电角度;u1、φ1分别为基波电压的幅值和初始相位;u5、φ5分别为5次谐波电压的幅值和初始相位,u7、φ7分别为7次谐波电压的幅值和初始相位,在永磁体磁场作用下,5、7次谐波电压产生的6、12次谐波转矩方程为
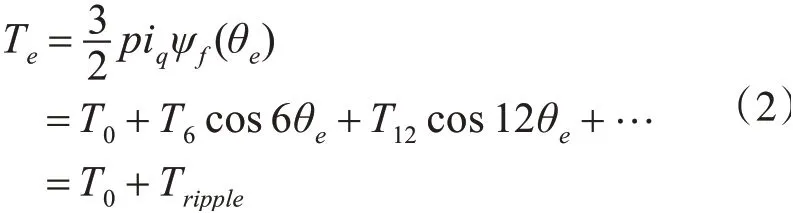
其中,T0、T6、T12分别为直流转矩、6次和12次谐波转矩幅值;Tripple为总的谐波转矩。
3 迭代学习控制抑制周期性转矩脉动
迭代学习控制于20世纪80年代由Arimoto等首次提出,是一种对做重复运动的轨迹跟踪系统的控制方法[10]。该算法通过多次利用先前的控制信息来产生期望输入,通过在线迭代学习找到合适的输入信号,使得被控变量获得较好的跟踪轨迹。本文设计了一种带遗忘因子的开闭环PID型迭代学习控制器,将传统转速调节器的输出电流作为系统跟踪对象,系统输出电磁转矩为反馈,将两者偏差信号经迭代学习控制算法实时补偿到q轴电流的给定端,使其误差在不断重复迭代中减小,使得系统输出转矩较好地跟踪速度调节器的输出,最终达到转矩周期性脉动抑制的效果。
3.1 迭代学习控制律
本文采用带遗忘因子的开闭环PID型迭代学习控制算法进行转矩周期性脉动抑制,迭代学习控制框图见图1,迭代学习控制律的数学描述为
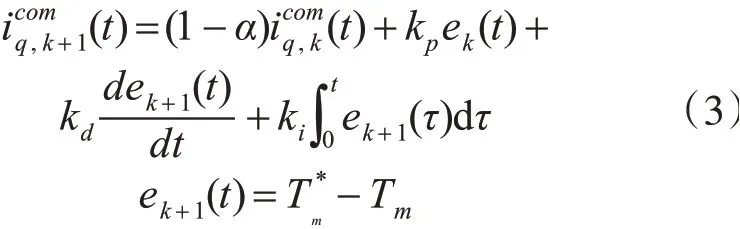
3.2 基于迭代学习控制器的PMSM系统
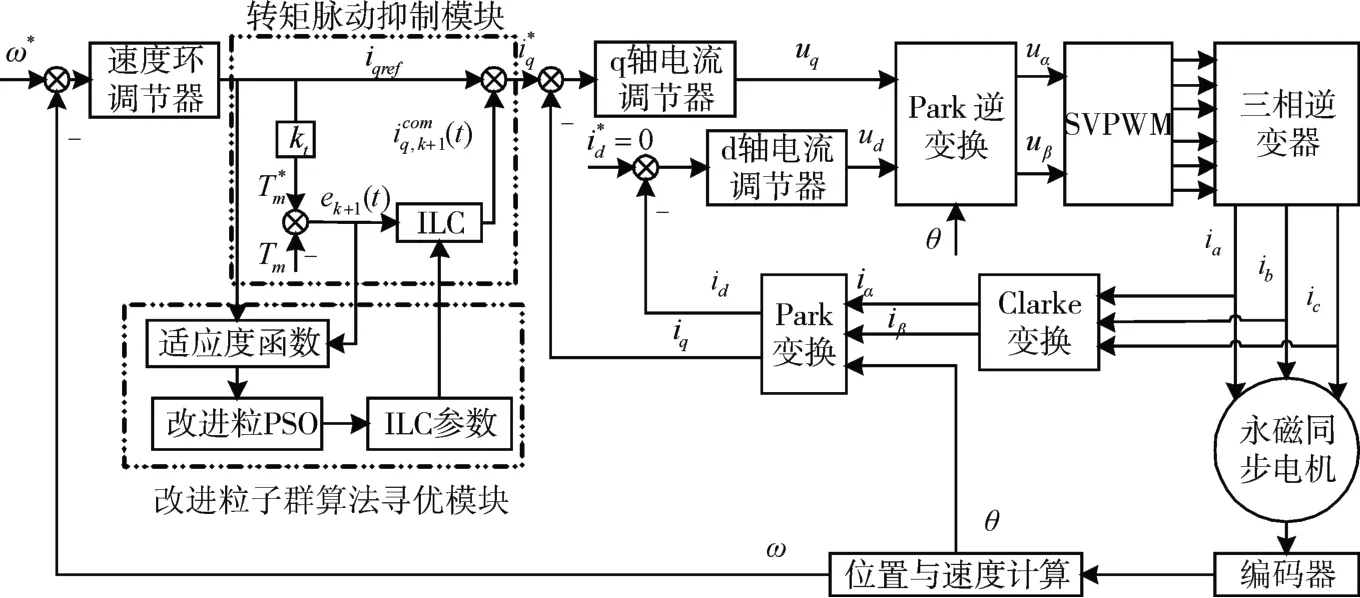
图2 基于迭代学习控制的永磁同步电机系统框图
4 改进粒子群算法对ILC的参数寻优
为获得更好的转矩脉动抑制效果,本文采用改进粒子群算法对迭代学习控制其中的四个关键参数kp、ki、kd和遗忘因子α进行优化整定。考虑到标准粒子群算法存在“早熟”收敛、容易陷入局部最优解和后期搜索精度不高等缺陷[13~14]。对此,提出一种改进的粒子群算法,将遗传算法中杂交的概念运用到粒子更新迭代中,提高粒子多样性、增强粒子全局探索能力[15]。同时,惯性权重根据粒子当前适应度优秀程度进行分类调整,标准粒子群算法为
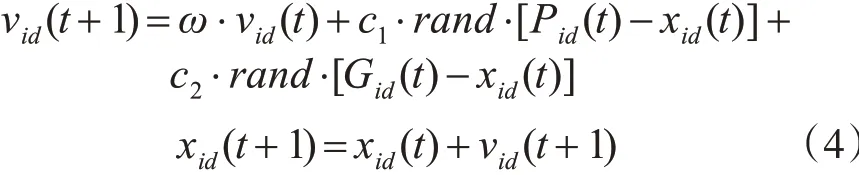
其中,vid和xid分别为粒子的速度和位置;ω为惯性权重;rand为0与1之间随机数;Pid为粒子i第d维的个体最优值;Gid为种群在d维空间的全局最优值;c1、c2为学习因子。本文选取的适应度函数:
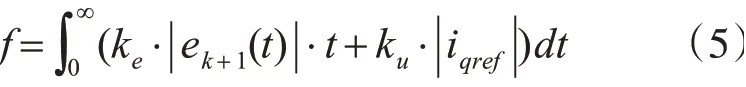
式中,ke、ku为权重系数,f越小,表明相应粒子越靠近全局最优解。由于本文最终控制目标是使得电机启动后稳态运行过程中输出转矩脉动较小,实际中很难在线测量转矩脉动参数,经多次试验,发现该适应度函数的大小与转矩脉动程度呈正相关,因此采用间接的适应度函数来间接表示转矩脉动大小。最优的迭代学习控制器参数就是f最小时所对应的的粒子位置。
4.1 改进PSO算法
设定粒子i的适应度值为fi,当前粒子最优适应度值为fmin,粒子群的平均适应度值为favg,将优于平均适应度值的粒子适应度值求平均,记为根据favg和f'avg这两个节点将空间中的粒子种群分为三类:适应度值小于f'avg的粒子记为子群Ⅰ,将适应度函数值介于favg和f'
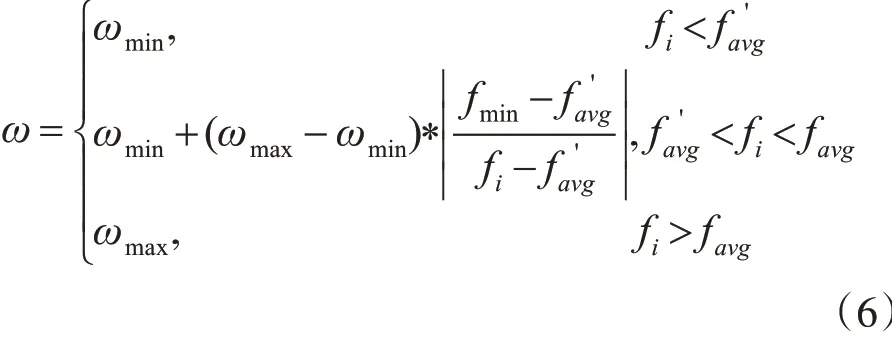
avg之间的粒子记为子群Ⅱ,将适应度函数值大于favg的粒子记为子群Ⅲ;根据所分三类子群分别进行不同的自适应操作,三类子群的惯性权重更新如下:其中,ωmin为惯性因子最小值,ωmax为惯性因子最大值;对于子群Ⅰ,粒子的适应度值较优,成熟度比较高,有较大可能在自身附近内搜索到最优值,此时应减小惯性权重,提高粒子的局部搜索能力;对于子群Ⅱ,粒子的适应度值为中等,具有中等成熟度,惯性权重的大小应兼顾自身经验和群体经验进行选取;对于子群Ⅲ,粒子的适应度值较差,成熟度较差,几乎不能在自身范围内搜索到最优值,此时应增大惯性权重,提高粒子的全局搜索能力。
同时,在标准粒子群算法的基础上加入杂交的操作,在每次迭代中,根据杂交概率选取一定数量的父代粒子随机两两杂交生成同等数目的子代粒子并替代父代粒子,杂交公式为
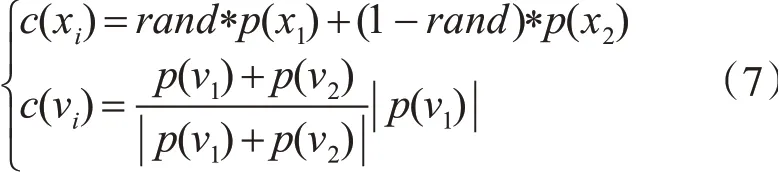
其中,c(xi)和c(vi)分别为子代的位置和速度;p(xi)和p(vi)分别为父代的位置和速度。
4.2 算法寻优步骤
基于改进PSO对迭代学习控制参数寻优具体步骤如下。
Step1:初始化,采用随机方式对kp、ki、kd和α这四个粒子的速度和位置进行初始化,给定最大迭代次数T,种群规模n,粒子维度d。
Step2:将kp、ki、kd和α位置带入ILC,运行系统,根据式(5)计算并评价当前粒子作用下的的适应度f,将粒子的位置和适应度存储在粒子的个体极值Pid中,将所有Pid中最优适应度值的个体位置和适应度值保存在全局极值Gid中。
Step3:根据式(6)更新惯性权重。
Step4:根据式(4)更新下一代粒子的位置和速度,同时根据适应度值f,评价粒子位置的优劣,比较当前所有的Pid和Gid,并更新Gid。
Step5:由式(7)生成杂交后的子代粒子并替换父代粒子,保持Pid和Gid不变。
Step6:达到当前最大迭代数或适应度函数足够好时,停止搜索并输出kp、ki、kd和α的位置信息,否则返回Step2。
5 仿真实验
5.1 Matlab仿真实验
在Matlab中,采用M语言编写改进的PSO寻优整定算法程序,并在Simulink中搭建基于迭代学习算法的PMSM双闭环模型。对迭代学习控制器中的四个参数进行寻优整定,其取值范围分别为kp∈[0,20],ki∈[0,20],kd∈[0,20],α∈[0,1],种群规模n=20,粒子维度d=4,最大迭代数T=100,
c1=4,c2=2,ωmax=0.9,ωmin=0.4,ke=100,ku=1,
Simulink中相应参数设置如表1。
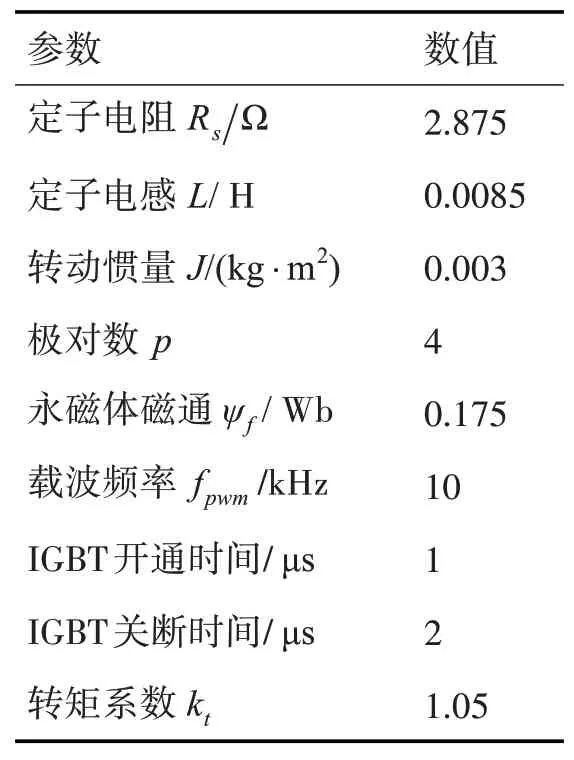
表1 Simulink仿真参数
给定转速500 r min,恒定负载10 N·m。经改进PSO寻优整定后得到迭代学习控制器的最优参数如表2,适应度函数收敛曲线见图3。

表2 改进的PSO寻优整定后结果
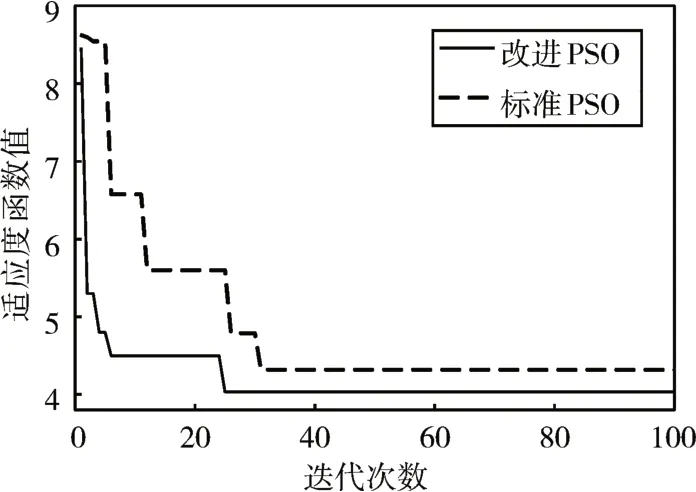
图3 适应度函数收敛曲线
由图3可知,相比于标准PSO算法,改进的PSO算法在第6次就找到了收敛区间,搜索速度快,于第25次迭代成功跳出“早熟”收敛,最终找到全局最优适应度值,并确定此时ILC控制器的4个参数。为验证本文方法的有效性,将本文的方法和文献[5]、文献[6]的方法的转矩脉动抑制效果进行对比,结果如图4。
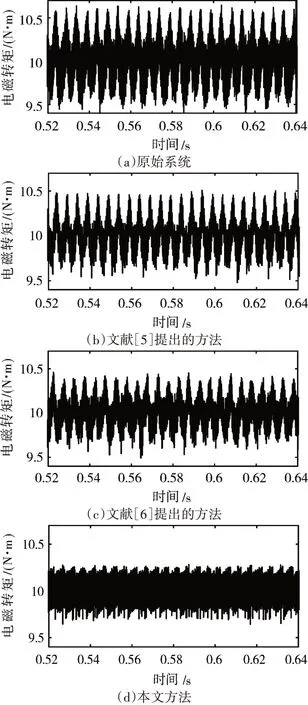
图4 三种方法转矩脉动抑制效果图
图4 (a)为原始系统输出电磁转矩,图4(b)、图4(c)、图4(d)分别为采用文献[5]、文献[6]和本文提出方法的转矩脉动抑制效果,三种抑制策略下对比可知,在恒定转速恒定负载转矩条件下,本文提出的方法相比于文献[5]和文献[6]具有较好的效果,使得输出转矩脉动幅值较小。采用转矩脉动系数(Torque Ripple Factor,TRF)评价抑制效果,TRF公式为
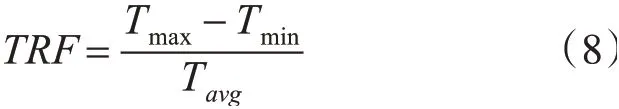
式中,Tmax为转矩最大值,Tmin为转矩脉动最小值,Tavg为输出转矩平均值,转矩脉动系数反映了电机输出转矩稳态时在给定目标值附近脉动的剧烈程度[16]。三种方法对应的转矩脉动系数对比如表3。
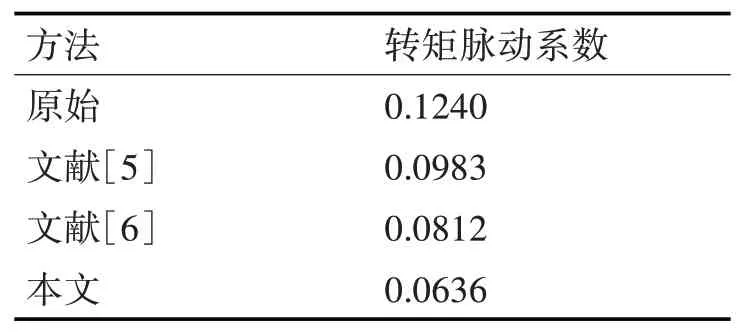
表3 三种方法对应的转矩脉动系数
通过对比可知,本文提出经参数优化后的ILC转矩脉动抑制效果相比于文献中的两种方法,拥有较低的转矩脉动系数。同时采用快速傅里叶变换(Fast Fourier Transform,FFT)分析电机定子电流以及电磁转矩中谐波分量的抑制效果,设定三相电流基频率为33Hz,得到各次谐波含量对比如表4。
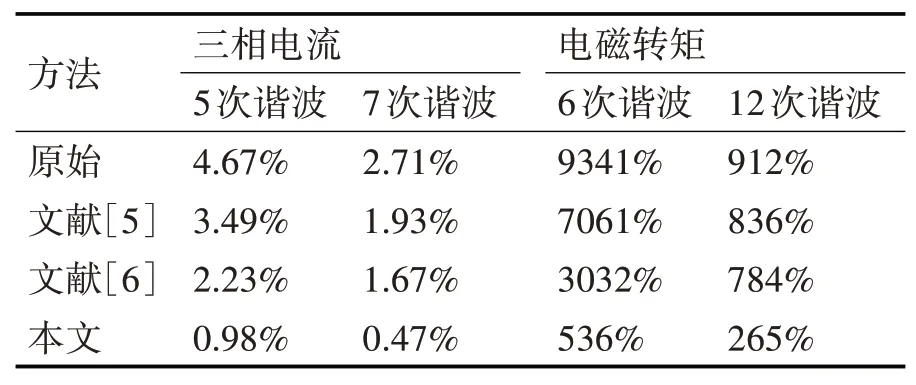
表4 三种方法各次谐波含量对比
由FFT分析可知,在原始系统的基础上采用文献[5]、文献[6]所提出的转矩脉动抑制策略后,定子三相电流和输出电磁转矩中的谐波分量均得到了有效抑制。在本文提出的抑制策略下,定子三相电流中的5、7次谐波含量分别由原来的4.67%和2.71%降为0.98%和0.47%,同样的,电磁转矩中的6、12次谐波含量分别由9341%和912%降为536%和265%。由此可见,在三相电流和电磁转矩的谐波分量抑制方面,本文提出的方法取得了较好的效果,要优于其他两种方案。
5.2 实验平台验证
为进一步验证本文提出方法的有效性,通过750W的PMSM矢量控制平台对该算法进行对比试验,实验平台如图5所示。

图5 实验硬件平台
实验系统以MKV56F512Vxx24为控制核心,永磁同步电机额定参数为pN=750W,UN=280V,nN=3000 r min,Ld=0.36mH,Lq=0.15mH,Rs=64 mΩ,φf=0.07Wb,逆变器死区时间设定为10 μs,转子惯量值为0.009 kg·m2,负载惯量为10倍转子惯量。在给定转速n*=100 r min条件下,通过Lab⁃VIEW上位机监控系统进行监测和采集数据,对比加入优化算法前后q轴电流脉动幅度,结果如图6。

图6 优化前后q轴电流对比
由图6可以看出,在加入本文提出的优化算法之后,电流波形有了明显改善,q轴电流的脉动幅度也得到了有效抑制。从实际的实验结果可以看出,本文提出的经参数优化后的迭代学习的控制算法可以有效地抑制永磁同步电机转矩周期性脉动。
6 结语
针对永磁同步电机运行时存在转矩周期性脉动的问题,在传统的转速电流双闭环矢量控制系统的基础上,通过迭代学习控制的在线学习能力实时补偿转矩电流给定来抑制转矩脉动,利用改进的粒子群算法对迭代学习控制器中的关键参数进行寻优整定,进一步提升了转矩脉动抑制的效果。同时对比迭代学习控制在转矩脉动抑制应用上的其他两个方案,本文方法的效果更为明显。最后搭建硬件实验平台验证算法的可实现性和有效性。
