一种基于高精度地图匹配误差的路径规划方法*
2021-12-01任明武
訾 烨 任明武
(南京理工大学计算机科学与工程学院 南京 210094)
1 引言
近年来,随着信息工业的不断进步,无人驾驶得到了密切关注和极大发展。在无人驾驶领域中,一个标识准确且包含丰富信息的地图是十分重要的,它能够帮助无人车定位和配准,并作为后续路径规划的基础。目前使用最广泛的地图构建、匹配、定位与导航技术是基于全球卫星导航系统(Global Navigation Satellite System,GNSS)与惯性导航系统(Inertial Navigation System,INS)相结合、并辅以动态实时差分方法(Real-time kinematic,RTK)进行误差修正的技术[1]。但是,由于以GNSS技术为基础的导航只精确到米级,且极易受到地形及卫星信号的影响,人们渴望构建一种更精准、更稳定且包含更丰富语义信息的高精度地图。
高精度地图是指精细化定义的地图,其精度需要达到分米级才能够区分各个车道。而精细化定义,则需要格式化存储交通场景中的各种交通要素,包括传统地图的道路网数据、车道线和交通标志等数据。基于高精度地图的匹配定位作为近年来无人驾驶领域研究的热门问题,已经积累了一定经验,提出了多种用于高精度地图匹配定位的算法。其大致可以分为基于地图特征的匹配定位和基于扫描的匹配定位两种。基于地图特征的匹配通常需要向地图中添加特定的语义特征信息,本质上仍然是概率统计,且在极大程度依赖GNSS所提供的米级精度的数据。为了解决这一问题,基于扫描的匹配定位方法越来越得到重视。基于扫描的匹配定位方法要求高精度地图中包含构建地图时的点云数据,通过比较当前扫描点云和地图点云确定车辆相对于地图的姿态。扫描匹配通过点的匹配来完成定位,其中最经典的算法是迭代就近点算法(Iterative Closest Point,ICP)[2]。但是,ICP算法有运算时间长、对初始姿态要求高、容易陷入局部最优等缺点。为解决这一问题,2003年,P.Biber和W.Strasser等提出了正态分布变换匹配算法(Normal Distributions Transform,NDT)[3]。由于NDT算法不利用对应点的特征进行计算,所以其运算速度比ICP快,且不会陷入局部最优。
同时,由于NDT算法会输出在地图的不同点处的匹配准确率,该匹配准确率在一定程度上会影响基于该地图的路径规划。因此,要想提高基于高精度地图的路径规划的置信度,必须在路径规划中考虑到匹配与定位准确率的问题。传统的路径规划算法可以分为图搜索法、人工势场法、随机地图法和智能化算法四类。每一类方法自成体系,都各有其优缺点。考虑到代价函数的灵活性和应用场景的广泛性,以A*算法[4]和蚁群算法[5]为代表的智能化算法得到了越来越多的重视,逐渐成为主流使用的路径规划算法。
本文拟采用致密的激光雷达点云数据作为高精度地图的数据来源;然后使用NDT算法进行匹配与定位,并输出匹配准确率;最后将匹配准确率与局部路径规划算法的代价函数相结合,完成局部路径规划。
2 算法描述
2.1 NDT算法
2003年,P.Biber和W.Strasser等提出了一种范围扫描的替代表示形式,即为正态分布变换(Nor⁃mal Distributions Transform,NDT)[3],该分布在本地模拟测量点的概率。转换的结果是分段的连续且可微的概率密度,可以使用牛顿算法将其用于匹配另一次扫描。2006年,Takashi Tsubouchi等提出了一种将2D-NDT扫描匹配方法扩展到3D扫描匹配的方法,首次提出了3D-NDT的概念并对其进行了改进以加快处理时间[6]。2010年,Todor Stoyanov等在3D-NDT的基础上提出了一种路径规划的新颖方法,该方法修改了著名的波前计划器,以使用3D-NDT作为地图表示的基础,并使用室内和室外数据集进行评估[7]。2013年,Jari Saarinen等提出了一种新颖的3D映射方法-正态分布变换占用图(NDT-OM),来解决现实世界地图的挑战[8]。
NDT算法的核心思想是把二维或三维点云数据集转化为连续可微的、多维变量的正态分布函数。NDT算法首先把参考点云(reference scan)所在的空间划分为指定均匀大小或形状的网格,并分别计算每个网格的正态分布参数均值μ和协方差矩阵∑:
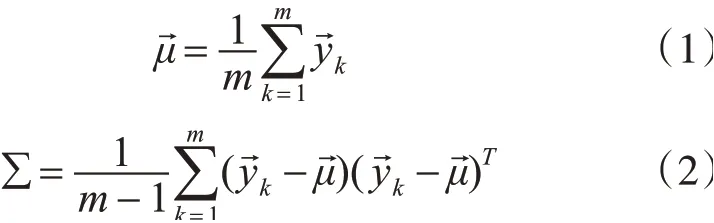
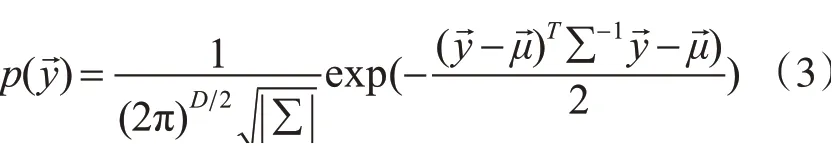
得到每个点的概率分布后,就可以根据正态分布参数计算每个点的概率密度,继而得到NDT配准得分(score),判断配准准确率。
2.2 A*算法
A*算法是一种运用最广泛的启发式搜索算法。A*算法的基本理论是计算当前节点可能到达的每个相邻子节点的评估值。当路径搜索过程扩展到某节点时,需要将该节点与所有已扩展的节点进行比较。如果该节点是扩展节点,则表明已找到到达该节点的新路径;如果新路径使该节点评估值较小,则必须修改该节点使它指向新路径的新父节点。最后,该算法选择最小评估节点以按顺序展开并将其放入封闭表中。
算法的基本步骤描述如下。
1)将地图转化为栅格化的网格表示;
2)首先设置open列表和closed列表,open列表用于记录所有被考虑用来寻找最短路径的节点,closed列表用于记录不会再被考虑的节点;
3)计算各个节点i的评估函数f(i)=g(i)+h(i),其中g(i)代表从起点到当前点i的移动量,h(i)表示从当前点到目标点的移动量估算值,该估算值是不确定的,有可能受到地图上其他因素的影响;
4)将起点s加入open列表,并查看所有与其相邻的节点,选择其中可走的(walkable)或可到达的(reachable)节点也加入open列表;
5)选择open列表中的评估函数值f(i)最小的节点,将其从open表中删除,加入closed表,并检查其相邻的所有节点。若有节点满足在closed表中是不可走的unwalkable,则忽略它,否则转6);
6)若该节点不在open表中,则将它加入open表,将当前节点设置为它的父亲节点,并计算f(i),否则转7);
7)若该节点已在open表中,则检查这条路径是否是更好的路径(若其g(i)更小,则代表这条新路径更优),若是则将其父亲节点设置为当前节点,并重新计算其g(i);
8)重复步骤5)~8),直至将终点加入open表或open表已空。前者输出最优路径,后者表示没有最优路径。
3 基于NDT算法的地图匹配及同步路径规划
基于NDT算法的地图匹配及同步路径规划算法的步骤如下图所示。具体步骤可描述为:1)首先将处理过的高精度地图网格化;2)使用NDT算法完成地图匹配与定位;3)最后基于地图匹配输出的匹配准确率,使用A*算法进行局部路径规划。
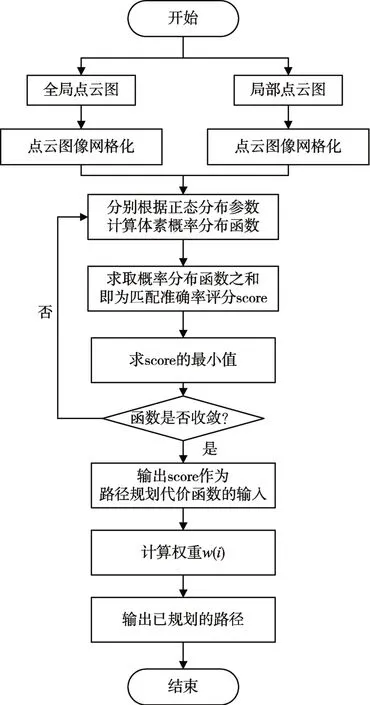
图1 本文改进算法流程图
3.1 高精度地图网格化
网格数据是以规则的阵列来表示空间地物或现象分布的数据组织。每个网格代表一个至多个像素,并包含能够表示该像素的数据类型或数量。一般来说,网格划分大小越大,包含的像素个数越多,表达的语义信息越少;网格划分大小越小,其包含的像素个数越少,表达的语义信息越多[9]。因此,在定义网格大小时,应当平衡每个网格包含的信息数量和信息精确度的关系,选择合适的网格大小。
本文使用八叉树(Octomap)的格式进行地图的存储。首先使用三维激光扫描仪获取环境的三维点云地图,然后将其转换为八叉树数据结构。八叉树是一种树形的数据存储结构,除了空树外,八叉树中的每个节点都有八个或零个子节点。八叉树的格式存储方便,节省空间,且有利于使用二分法进行查找。对三维八叉树地图进行任意一个方向的投影,即可得到二维占据栅格地图[10]。
3.2 基于NDT算法的地图匹配
本文使用基于NDT的点云匹配算法完成地图的匹配与定位。NDT算法中尤其需要重视的是四个参数的设置,分别是最小转换差异(Transforma⁃tion Epsilon)、搜索的最大步长(Step Size)、网格结构的分辨率(Resolution)、匹配迭代的最大次数(Maximum Iterations)[11]。
NDT网格结构的分辨率即为均分的网格大小,网格的大小设置应合理,能够帮助计算和优化网格内每一点的存在概率。网格精度一般以为数据精度的3~5倍为宜,在本文中网格大小设置为5cm*5cm大小。
NDT算法使用More-Thuente线搜索用以确定搜索的最大步长,该方法试图使用包围以及二次和三次插值找到满足下降条件和曲率条件的一个点,用来确定最大步长值范围内的最佳步长。最小变换差异参数一般用作算法的终止条件,分别从长度和弧度定义了变换矩阵的最小许可递增量,一旦递增量减小到这个临界值以下,那么配准将终止[12~13]。
算法的基本步骤描述如下:
1)首先,将参考点云网格化,并计算每个网格的多维正态分布参数均值和协方差矩阵∑;
2)初始化变换参数p=(tx.ty,φ)T;
3)通过变换T将待配准的点云转换到参考点云的网格中:其中,表示待配准的点云网格内所有扫描

点,变换T可描述为
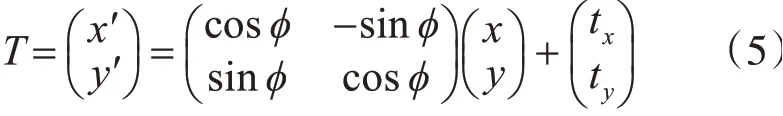
5)NDT的配准得分(score)为每个网络计算出的概率密度之和:
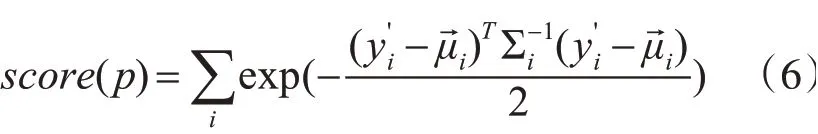
6)使用Hessian矩阵和牛顿迭代法对score(p)求最小值,利用如下函数:

其中g是score(p)的转置梯度,H是score(p)的Hessian矩阵。
7)重复步骤3)~6),直至达到收敛条件为准。
结束匹配后,可以输出NDT的配准得分值(score)对应的匹配准确率作为输出,引导后续的路径规划。
3.3 基于匹配误差的同步路径规划
本文使用A*算法进行基于匹配误差的局部路径规划。A*是一种应用十分广泛的启发式搜索算法,它依赖启发信息构造启发函数,并在规划路径时对所访问或待访问的节点进行代价评价,选择其中代价最小的、同时可满足要求的节点进行路径规划[14]。
由于在高精度地图的不同点处的匹配误差也有所不同,将匹配误差作为计算代价的一部分是很有必要的[15]。如果该点的匹配误差大,则认为该点附近区域的局部地图置信度较低,该区域内的障碍物对路径规划带来的风险就大;反之,若该点匹配误差小,对该区域内的障碍物的描述和判断也更加准确。因此,本文将NDT匹配算法输出的匹配准确率作为A*算法代价函数的输入,辅助路径规划代价评估。
在A*算法中,标准的启发函数使用欧氏距离,从u点到v点的欧式距离应表示为
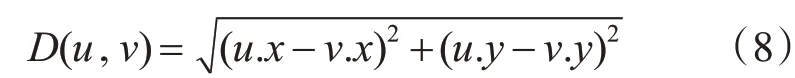
则评估函数中从u点移动到v点的实际移动距离G(u,v)应为从u点到v点的距离D(u,v)与v点的权重w(v)的乘积,表示为
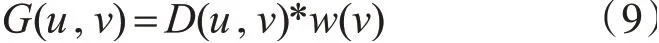
为使用NDT匹配算法输出的匹配准确率来指导路径规划,本文将该值引入A*代价函数中的某点的权重值w(i),i点处准确率越高,说明原始点云和待配准点云越相似,配准效果越好,经过i点的代价越小。因此,w(i)与该点的匹配准确率p之间的关系可表示为
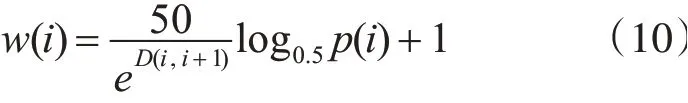
因此,本文中使用的A*代价函数可表示为
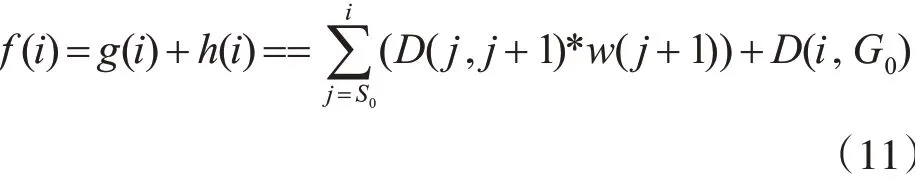
4 仿真实验结果与误差分析
为了验证NDT算法对于高精度地图的匹配的适用程度,并同时评估使用地图匹配误差指导的局部路径规划算法的有效性,本文分别对地图匹配算法和路径规划算法进行了仿真实验和评估。
4.1 基于NDT的高精度地图匹配
本文使用致密的高精度点云数据作为高精度地图的数据源,将全局地图记为scan1(如图2所示),并将其转化为用八叉树结构表示的三维八叉树地图,向地面投影,去除噪点后得到俯视的二维网格图(如图3)。在序列的局部点云图像中任取5帧(分别记为scan2-1至2-5,以scan2-3为代表表示为图4)与全局地图进行匹配,从而确定局部地图在全局地图中的位置,进而确定该区域在二维网格图中的位置(如图5)。

图2 全局点云图像scan1
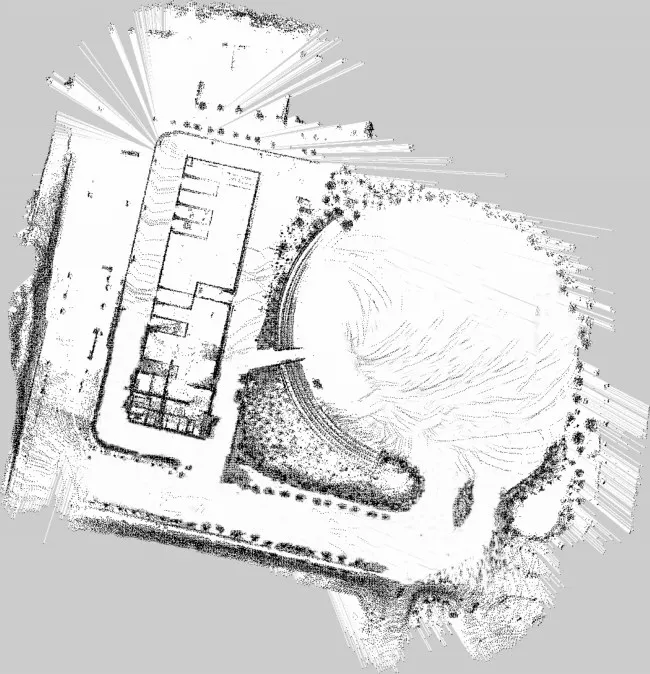
图3 scan1转化的全局二维网格图像

图4 局部点云图像scan2-3

图5 scan2-3对应的二维网格区域
图6 中列出了实验所选取的每帧对应的匹配准确率,可以看出,在使用同一套NDT算法参数的情况下,不同场景的匹配准确率是不同的。
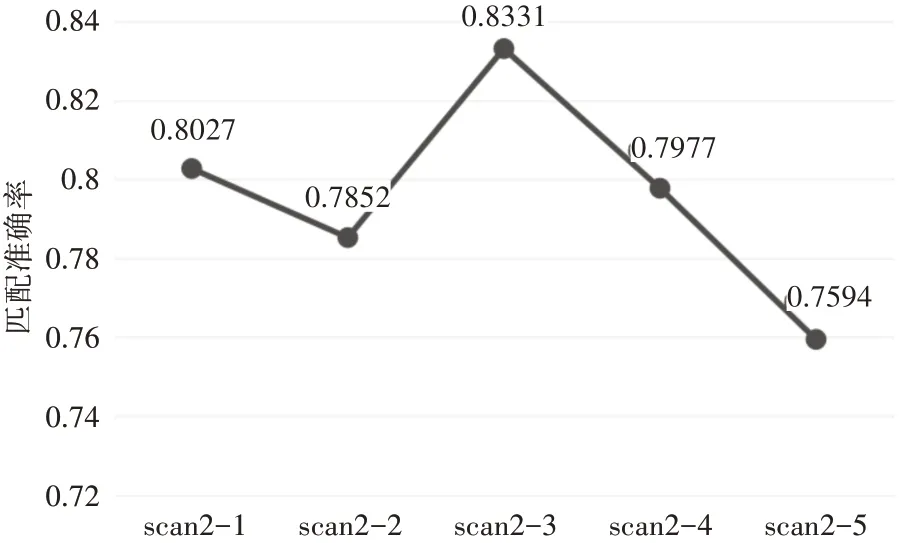
图6 匹配准确率变化展示
4.2 基于地图匹配误差的局部路径规划
本文分别对基础的A*算法和使用地图匹配误差进行改进的A*算法在简化的scan2-3对应二维网格图中进行仿真实验,实验结果分别如图7(a)和(b)所示。

图7 原始A*算法与本文的改进A*算法实验结果图
表1 中列出了A*与改进A*两种算法在仿真实验中的性能指标衡量结果,该表列出的三项指标为50次实验的平均值。在表中,运行时间表示算法在地图中遍历寻找最优路径的时间、危险网格数表示障碍物周围危险系数大于0.5(代价w大于2)的网格个数、潜在危险程度表示规划出的路径经过危险网格的个数。

表1 A*与本文改进A*的结果评价
从图7(a)、(b)及表2中数据可以看出,使用地图匹配误差进行改进的A*算法在基本不增加遍历时间的条件下,明显降低了规划出路径的潜在危险程度,使得无人车在行驶过程中能够更加稳定。
改进算法对障碍物周边网格危险程度的判断主要基于地图匹配误差的准确率。若准确率越高,匹配误差越小,障碍物周边网格的危险程度越小。图8(a)为匹配准确率0.8331的局部地图,图8(b)为匹配准确率0.7594的局部地图,可以看出,算法在图8(a)中障碍物辐射的危险范围明显小于图8(b),在(a)中无人车经过障碍物周边网格的代价也低于(b)。

图8 不同匹配误差下的局部路径规划情况

5 结语
高精度地图作为一种表达道路信息的更为精确、包含语音信息更丰富的形式,在当今的无人驾驶领域起到越来越重要的作用。因此,研究基于高精度地图的地图匹配及同步路径规划也是有其重要意义的。本文提出了一种将基于高精度地图的匹配误差引入路径规划算法的路径规划方法。实验证明,这种方法在保证路径规划效率的同时,也使得全局路径规划更加合理,避开更多的障碍,付出更少的代价。
