基于干扰重构和分数阶滤波的频谱弥散干扰抑制
2021-11-30余康林匡华星王超宇
余康林,匡华星,王超宇
(中国船舶集团第七二四研究所,南京 211153)
0 引 言
线性调频信号是脉冲压缩雷达常用的一种发射信号形式,因其具有较大的时宽带宽积,使得雷达能够同时拥有较优的距离分辨率和速度分辨率。针对该类型雷达,Sparrow等[1]提出了多种密集假目标干扰,如频谱弥散(Smeared Spectrum,SMSP)干扰、间歇采样转发干扰,其本质都是对干扰机截获的雷达发射信号进行调制转发,因此与雷达发射信号具有较强相干性,脉压处理后将在多个距离单元上形成假目标,因其与真实目标较为相似,增加了雷达目标检测的难度。根据Sparrow等对SMSP干扰不同参数下的干扰效果的分析,当SMSP干扰的调频率取为雷达发射信号的5~7倍时,干扰效果最优。对于SMSP干扰,考虑自卫式干扰场景下,干扰与真实目标回波混叠进入雷达接收机,由于干扰与真实目标回波时、频、空域上的高度混叠,传统的波束形成[2]、盲源分离[3]等抗干扰措施将会在干扰抑制的同时造成严重的信号功率损失,因此针对该干扰需要研究相应的抗干扰措施。
目前,针对SMSP干扰的抗干扰措施,主要包括干扰重构对消和干扰剔除。文献[4-5]根据SMSP干扰与雷达发射信号的关系,通过估计SMSP干扰子脉冲个数、时延、幅度和初始相位重构干扰并对消抑制SMSP干扰,但涉及对时延、幅度和初始相位的遍历估计,并存在较大误差。文献[6]基于压缩感知理论,通过构建干扰基字典及调频率匹配,能够自适应重构干扰,并通过对消抑制SMSP干扰,但需较大的计算量。文献[7]提出了基于干扰剔除的干扰抑制方法,由于SMSP干扰与真实目标回波的时频分布差异,通过剔除SMSP干扰时频点抑制SMSP干扰,但该方法会对目标回波功率造成一定损失。文献[8]提出了联合时频重排和双正交傅里叶变换的SMSP干扰抑制方法,利用Radon变换估计SMSP干扰子脉冲个数,并构建参考信号将SMSP干扰调制成一个线性调频信号,通过峰值滤波并解调重构SMSP干扰,最后通过对消抑制干扰,但是该方法计算量较大。
本文在现有研究基础上,根据干扰重构对消的思想提出了干扰重构的另一思路。仿真结果表明,所提方法计算量较小,能够获得较高的信干噪比增益,在干扰抑制后能够有效检测到目标。
1 SMSP干扰模型
自卫式干扰场景下,雷达回波模型可假设为
z(t)=s(t)+j(t)+n(t) 。
(1)
式中:t为时间变量,s(t)、j(t)、n(t)分别为真实目标回波、干扰和噪声。假设雷达发射信号为线性调频(Linear Frequency Modulation,LFM)信号,不考虑载频,则真实目标回波模型如下:
(2)

根据SMSP干扰产生原理[4],其数学模型如下:
(3)
式中:Aj、Tj、kj、t1、φj分别为SMSP干扰的幅度、脉宽、调频率、时延和初始相位,Tj、kj与T、k对应关系如下:
(4)
由式(4)可得,SMSP干扰包含m个子脉冲,每个子脉冲的脉宽为雷达发射信号脉宽的1/m,调频率为雷达发射信号调频率的m倍,m一般取大于1的整数。
2 SMSP干扰重构
由上述对SMSP干扰的分析可知,SMSP干扰与真实目标回波调频率存在较大差异,并且干扰功率一般远大于真实目标回波功率,因此较容易辨识出雷达回波中是否包含该干扰,若干扰与真实目标回波不存在混叠,则很容易将该干扰剔除,无法对雷达造成有效的干扰,因此SMSP干扰一般与真实目标回波存在一定的混叠。

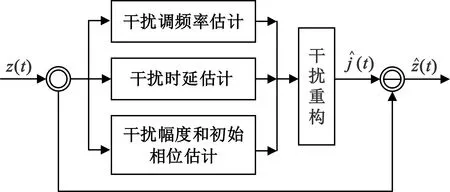
图1 基于干扰重构的SMSP干扰抑制方法流程图
2.1 SMSP干扰调频率估计
分数阶傅里叶变换(Fractional Fourier Transform,FRFT)常用于估计LFM信号调频率。对于信号x(t),其p阶分数阶傅里叶变换定义为

(5)
式中:Kp(t,u)定义为
(6)
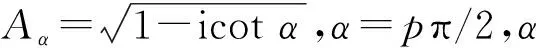
分数阶傅里叶变换对LFM信号具有能量聚集性,当LFM信号进行旋转角度为α=arccot(-k)的FRFT时,能量聚集效果最优,k为其调频率。Renyi熵常用于描述信号的能量聚集性[9]:信号的能量聚集性越高,Renyi熵越小;反之,Renyi熵越大。在对SMSP干扰进行最优旋转角度搜索时,可以用Renyi熵评价SMSP干扰不同旋转角度下的能量聚集性。由于回波中干扰功率远大于真实目标回波功率,因此最小Renyi熵对应的旋转角度即是SMSP干扰对应的最优旋转角度,再根据旋转角度与调频率之间的关系,即可得到SMSP干扰的调频率。设雷达回波z1,z2,…,zn离散分数阶傅里叶变换归一化幅度谱为X1,X2,…,XN,使其幅度之和为1,则Renyi熵定义为
(7)
式中:q为Renyi熵的阶次,一般取正整数,这里q取4。
由于SMSP干扰的调频率是雷达发射信号的m倍,因此其对应最优旋转角度一般位于雷达发射信号对应最优旋转角度的一侧,在雷达发射信号旋转角度已知的情况下,可以先以一个较大的角度搜索步长遍历正半区间或负半区间进行粗估计,再以较小角度搜索步长进行精估计。
SMSP干扰调频率估计步骤如下:

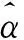
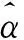
(8)
调频率估计相对误差定义为
(9)
在估计得到SMSP干扰的调频率后,根据SMSP干扰调频率与雷达发射信号调频率对应关系,SMSP干扰的子脉冲个数可由下式计算得到:
(10)
2.2 SMSP干扰时延估计
在估计SMSP干扰调频率和子脉冲个数的基础上,进一步估计该干扰对应的时延。构造参考信号h(t),其表达式如下:
(11)
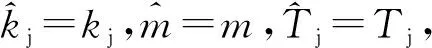

exp{i[πkj(t-t1-lTj-τ)2+φj]}dτ。
(12)
可得匹配滤波器输出幅度谱为
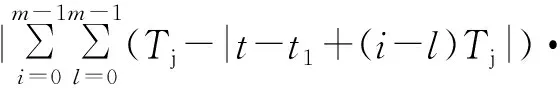
sinc[πkj(t-t1+(i-l)Tj)(Tj-|t-t1+(i-l)Tj|)]|,
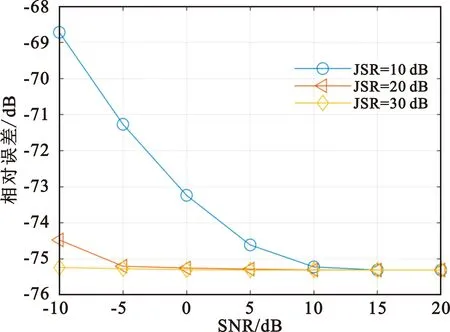
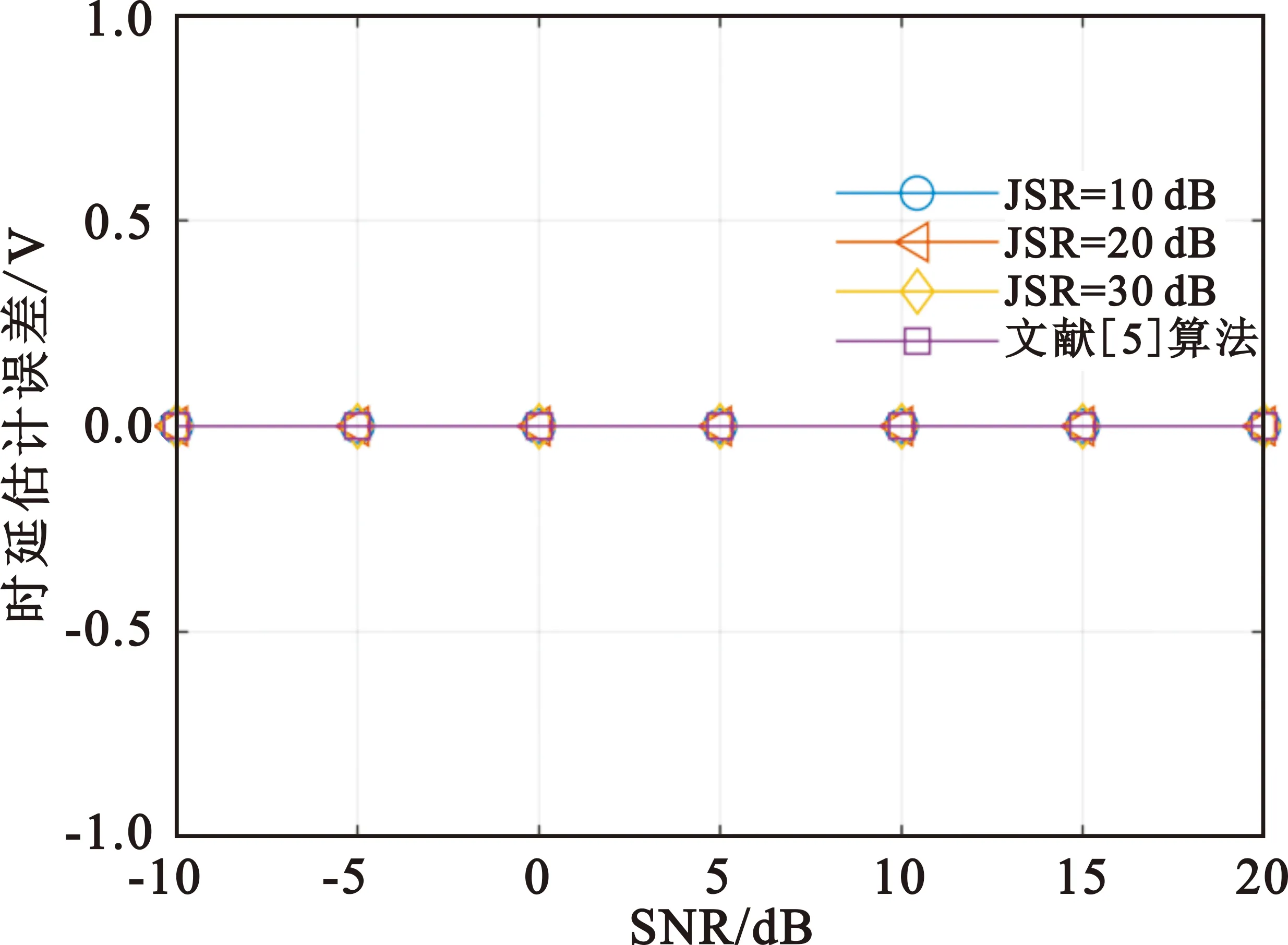
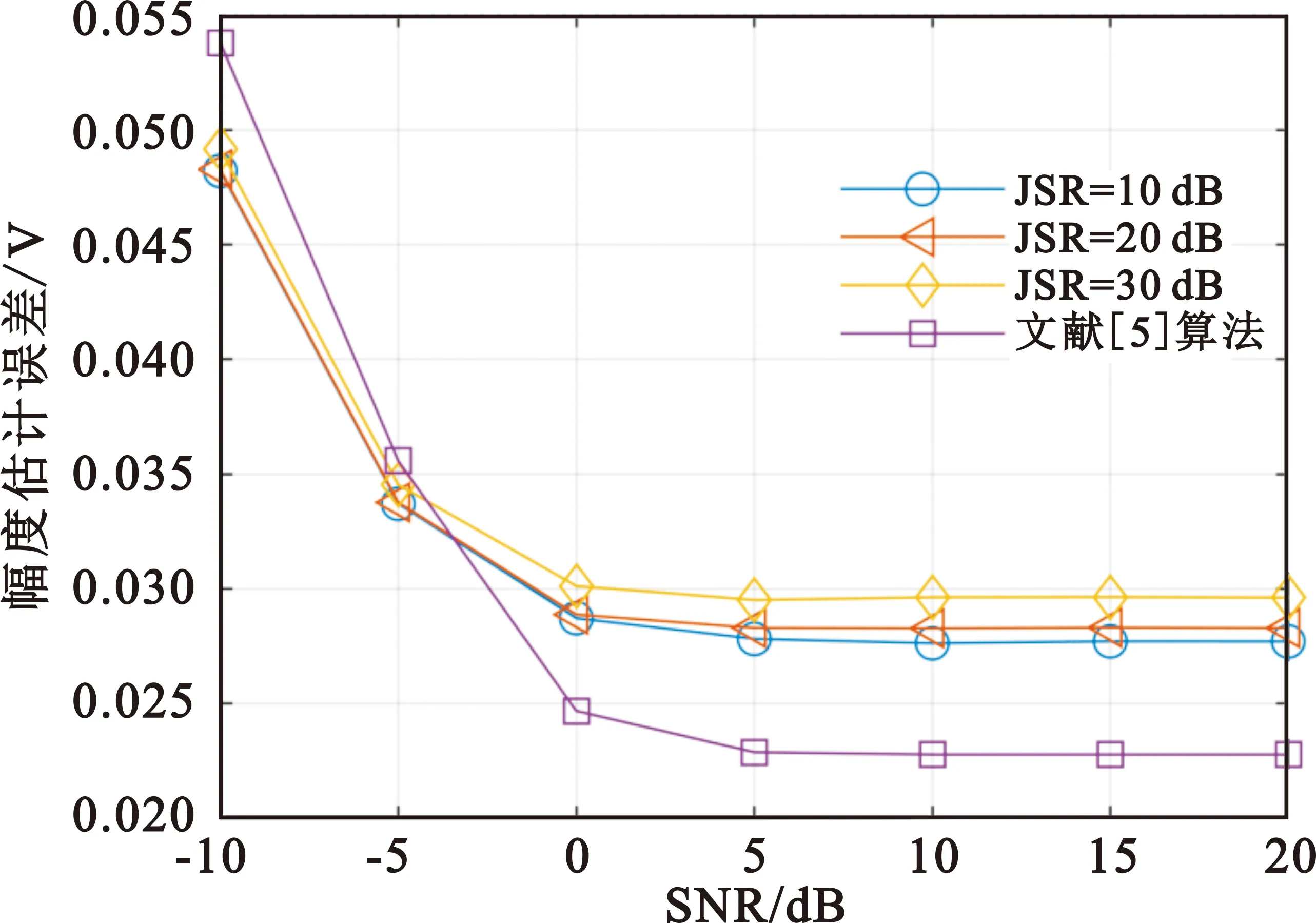
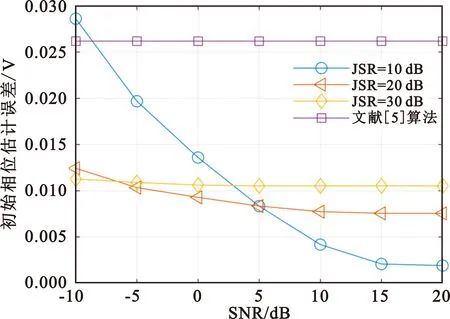
|t-t1+(i-l)Tj| (13) 对于雷达接收机采样得到的离散数据,可设为 (14) (15) 式中:Nj=N/m。 (16) TAjeiφje-i2πft1sinc(πTf)。 (17) 当f=0时,上式取得最大值,幅度为TAj,相位为φj。由于系数T已知,则SMSP干扰的幅度和初始相位可由下式计算得到: (18) 因此在SMSP干扰调频率、子脉冲个数和时延估计误差较小时,通过上述过程可以估计得到SMSP干扰的幅度和初始相位,在估计得到SMSP干扰的参数后就能重构该干扰,再利用对消抑制该干扰。重构的SMSP干扰表达式如下: (19) (20) |Xp(u)|=|sinc[πT(ucscα+kt0)]|, (21) 其输出表现为一个sinc函数,主瓣宽度为2|sinα|/T,此时分数阶傅里叶变换对真实目标回波具有最佳的能量聚集性,真实目标回波能量聚集在较窄的范围内,通过选择合适的滤波器,保留真实目标回波的主瓣能量,能够有效抑制残余干扰和噪声。 不失一般性,雷达发射信号的脉宽设置为10 μs,带宽设置为40 MHz,调频率为4 MHz/μs,真实目标回波及SMSP干扰参数设置如表1所示,干信比(Jamming-to-Signal Ratio,JSR)设置为10~30 dB,信噪比(Signal-to-Noise Ratio,SNR)设置为-10~20 dB,每个信噪比下进行10 000次蒙特卡洛实验。 表1 仿真参数 令干信比分别为10 dB、20 dB,信噪比为0 dB,真实目标回波与SMSP干扰参数设置如表1所示,不同干信比下雷达回波的脉压归一化功率谱及单元平均恒虚警率(Constant False Alarm Rate,CFAR)检测门限如图2所示。CFAR门限检测使用参数设置如下:参考单元数为60,保护单元数为8,虚警概率为10-6。由图2可知,当JSR为10 dB时,脉压处理后干扰不能压制住真实目标,经CFAR门限检测仍能有效检测到目标,此时无法有效干扰雷达;当JSR增加到20 dB时,脉压处理后真实目标被干扰完全压制,经CFAR门限检测无法有效检测到真实目标。因此对于SMSP干扰,需要JSR很大时才能有效干扰雷达。 (a)JSR为10 dB时脉压输出 令信噪比为-10~20 dB,干信比为10~30 dB,SMSP干扰和真实目标回波参数不变,分析上述参数估计方法估计SMSP干扰参数的误差,并对比干信比为30 dB时文献[5]的参数估计误差。SMSP干扰调频率估计时,粗估计搜索步长设为0.5°,i设为20,搜索精度设为0.000 5°。 SMSP干扰的调频率估计误差如图3所示。由图可知,随着信噪比的升高,SMSP干扰的调频率估计误差逐渐减小,这表明信噪比越高,噪声对SMSP干扰调频率估计造成的影响越小;信噪比一定时,随着干信比的升高,SMSP干扰的调频率估计误差越低,这表明当SMSP干扰功率在雷达回波中占比越高,真实目标回波功率对SMSP干扰调频率估计造成的影响越小。在估计得到SMSP干扰的调频率后,通过四舍五入取整,在上述仿真参数下均能准确估计得到SMSP干扰的子脉冲个数。文献[5]通过时延自相关估计SMSP干扰的子脉冲个数,干信比为30 dB时能够准确估计得到SMSP干扰的子脉冲个数及调频率。 图3 SMSP干扰调频率估计相对误差 图4 SMSP干扰时延估计误差 图5 SMSP干扰幅度估计误差 图6 SMSP干扰初始相位估计误差 令干信比为20 dB,信噪比为0 dB,采用上述干扰抑制方法后,脉压归一化功率谱如图7(a)所示,经CFAR门限检测能准确检测到真实目标的位置。不同干信比下,信干比增益随信噪比变化情况如图7(b)所示。信干比(Signal-to-jamming Ratio,SJR)增益定义为G=JSR1-JSR2,JSR1为干扰抑制前干信比,JSR2为干扰抑制后干信比。由图可知,干信比一定时,信干比增益随信噪比的提高逐渐提高,这是因为SMSP干扰的参数估计误差随信噪比的提高逐渐减小;信噪比一定时,信干比增益随干信比的提高逐渐提高,这表明当干扰功率所占比重上升时,干扰重构对消抑制掉的干扰功率增加;并且上述干扰抑制方法在较低干信比时也能达到29 dB以上的信干比增益。干信比为30 dB时,本文干扰抑制方法与文献[5]算法的信干比增益如图7(b)所示,从图中可以看出相同仿真条件下本文干扰抑制方法干扰抑制效果优于文献[5]算法。 (a)JSR为20 dB时干扰抑制后脉压输出 (a)干扰抑制后回波FRFT幅度谱 本文提出了一种基于干扰重构和分数阶滤波的SMSP干扰抑制方法,详述了SMSP干扰参数估计流程,并通过仿真实验验证了该方法的可行性。仿真结果表明,本文所提干扰参数估计方法具有较好的鲁棒性,在低信噪比下也能够精确估计得到SMSP干扰的参数,并且信干比增益仍能达到29 dB以上;在干扰重构对消的基础上,可以采用分数阶滤波进一步抑制残余干扰和噪声,以提高雷达回波信干噪比。
2.3 SMSP干扰幅度、初始相位估计
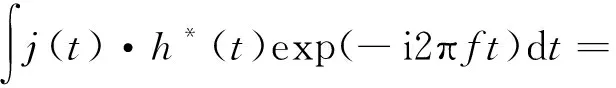

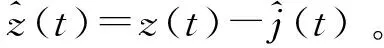
3 仿真与分析

3.1 SMSP的干扰效果

3.2 SMSP干扰不同参数的估计误差


3.3 本文方法的抑制效果


4 结 论
