一种空口波形非正交接入系统邻带干扰消除方法

邵 凯，李 慧

(重庆邮电大学 a.通信与信息工程学院；b.移动通信技术重庆市重点实验室，重庆 400065)

0 引 言

网络切片是第五代移动通信(5G)的基本功能，提供了一种可自定义虚拟子网对每个切片进行设计的方法,可以实现多个逻辑网络的经济高效部署和操作[1]。5G无线接入网络(Radio Access Network,RAN)将面临前所未有的挑战，以应对服务、设备类别、部署环境和移动性水平方面的高度异构性。在5G三种主要的通信场景[2-4]中，增强型移动宽带(Enhanced Mobile Broadband,eMBB)、大规模机器类型通信(Massive Machine-Type Communications,mMTC)以及超可靠和低延迟通信(Ultra-Reliable Low-Latency Communication,uRLLC)需适配不同的调制格式和多址技术。根据业务需求的多样性,RAN切片需要针对不同业务类型采用特定的物理传输波形配置，并在物理层将不同业务的信号打包传输[5]。新一代的无线通信要求在相邻频带中异步数字传输，不同业务要求具有不同参数物理波形的非正交接入，不可避免地造成相邻信道干扰(Adjacent Channel Interference,ACI)[6]。

因此，干扰消除是非正交接入系统中研究的热点之一。文献[7]采用预编码的方法来消除滤波多音调制(Filtered Multi-Tone Modulation,FMT)和交错正交幅度调制(Filterbank-based Multicarrier/Offset Quadrature Amplitude Modulation,FBMC/OQAM)之间的干扰，但是预编码方法主要改变了原型滤波器的系数，其操作过程具有很高的复杂度。文献[8]提出了一种预编码方案以抑制通用滤波多载波(Universal-Filtered Multicarrier,UFMC)系统之间的干扰，然而若要预先消除干扰，发射机需要来自接收机的准确的信道状态信息和噪声方差反馈，这在许多情况下不符合实际应用场景。文献[9]在数字混合参数传输的情况下为W-OFDM系统建立了一个不同数字参数干扰(Inter-Numerology Interference,INI)模型，利用已建立的解析模型对W-OFDM系统的INI特性进行了讨论和分析，提出了一种INI功率辅助干扰消除算法。但是此方法只适用W-OFDM系统，没有延展到其他系统。

综上所述，针对非正交接入系统中相邻信道干扰问题及相关研究存在的局限性，本文以经典的OFDM信号为例，提出了一种结合阈值截断与压缩感知恢复(Threshold Truncation and Compressed Sensing Recovery,TTCSR)的方法消除非正交波形的邻带干扰。相较于上述文献提出的干扰消除方法，通过设置阈值消除干扰是一种简单直接的方法，但由于阈值的设置，被截断的那部分信号会造成信号的失真，造成系统性能的下降。例如在处理OFDM系统的(Peak-to-Average Power Ratio,PAPR)问题时所采用的限幅法也是一种失真类方案[10-11]。其中文献[10]在接收端使用压缩感知(Compressed Sensing,CS)的算法来恢复由于限幅引起的OFDM信号的非线性失真问题。因此本文考虑在OFDM系统的接收端采用CS算法进行失真的消除，利用截断产生的失真信号的近似稀疏性，对整个信号失真进行建模。通过在接收端采用CS算法恢复失真，从而提升系统的误码率(Bit Error Rate,BER)性能。

1 系统模型

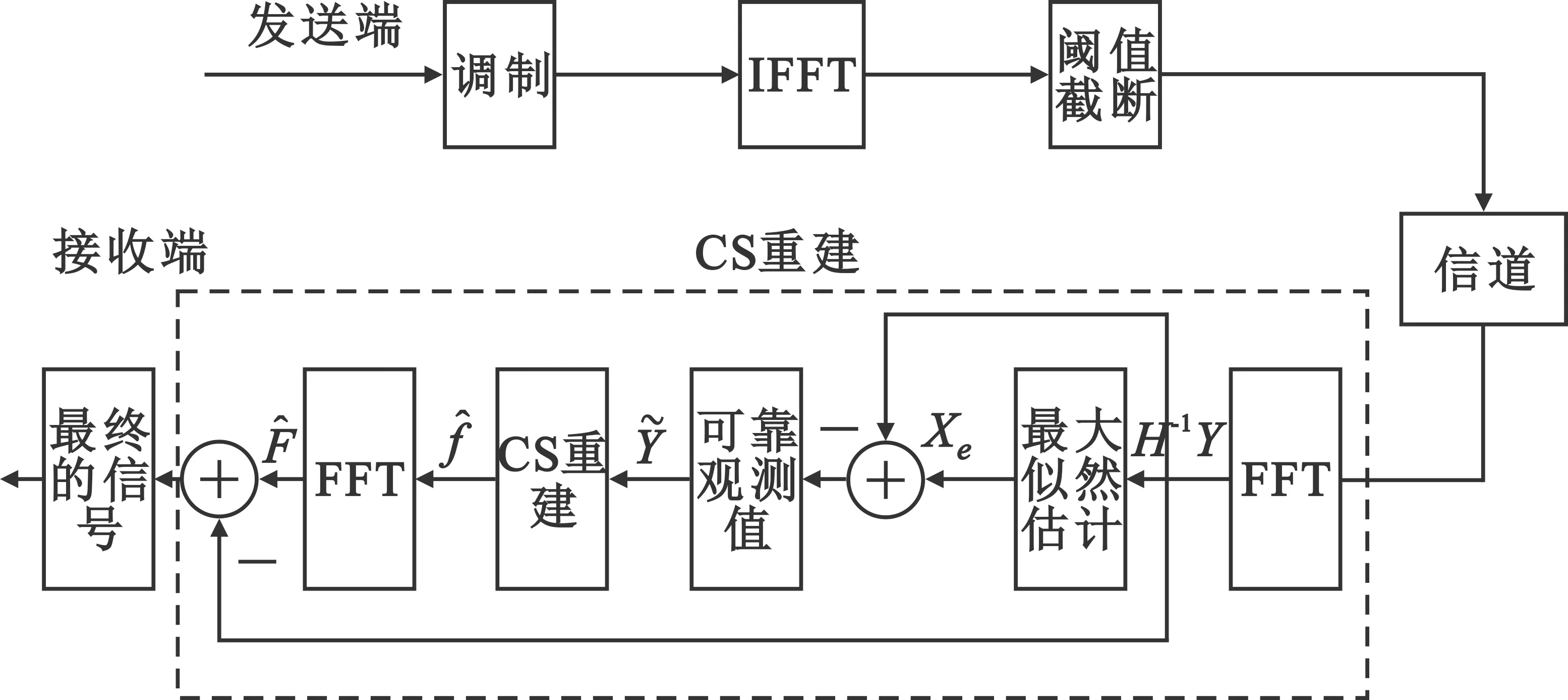
图1 TTCSR应用框图

两个异步系统在相邻信道非正交接入时通常用信号的功率谱密度(Power Spectral Density,PSD)来评估相邻信道两个系统之间的互干扰。以OFDM信号为例,两个系统之间的归一化互干扰[12]定义为

(1)

式中：l为两个OFDM信号相邻子载波之间的频谱距离；Δf为子载波间隔；φOFDM(f)为OFDM信号的功率谱密度函数，表示为

(2)

2 TTCSR算法

2.1 阈值选取

表1[12]给出了OFDM系统两个子载波随频谱距离变化的干扰功率PSD分析。基于PSD数据分析可以看出，OFDM信号在相邻子信道中传输时，邻近的第一个子载波的平均干扰值远大于其他子载波处的平均干扰值。随着干扰子载波的频谱距离的增大，对相邻信道子载波的干扰越来越小，因此可以根据OFDM子载波的归一化平均功率加上干扰功率来适当的设置阈值。

表1 OFDM的PSD干扰表[12]

子载波的归一化平均功率为P(n)，干扰功率设置为β，β的值由表1确定，阈值γ表示为

γ=P(n)+β。

(3)

根据阈值公式设置阈值，对高于阈值的信号进行截断可以得到截断后的信号，表示为

(4)

2.2 失真模型分析

通过对受到干扰的OFDM信号设置阈值进行截断可以有效消除干扰，但阈值截断会引起信号的截断失真。根据式(4)，发射端的实际传输信号可以表示为

(5)

(6)

式中：等式右边第一项αx(n)为原始信号的衰减部分；第二项d(n)为与原始信号的不相关项，满足E[d(n)]=0和E[d(n)x*(n)]=0，E[·]表示数学期望。

结合式(5)和式(6)可以得出失真噪声的频域表示为

F(k)=(α-1)X(k)+D(k)-C(k) 。

(7)

根据式(7)可得到频域失真噪声F(k)的平均功率为

E[|F(k)|2]=(α-1)2E[|X(k)|2]+

E[|D(k)|2]-E[|C(k)|2]。

(8)

式中：E[|C(k)|2]为信号受到干扰的功率β；α为衰减因子，表示为

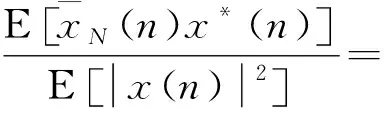
(9)

(10)

式中：s为信号的包络|x(n)|，ρx(s)为信号包络|x(n)|的概率密度函数(Probability Density Function,PDF)，对于较大的N值服从瑞利分布。

E[|D(k)|2]=2σ2D(k)=

(11)

2.3 接收端处理

由于当N足够大时OFDM信号的包络服从瑞利分布，x(n)可以看作是独立同分布的随机变量。截断产生的失真信号的非零个数远远小于整个频带OFDM信号的子载波个数，所截断的信号相对于整个频带的子载波可以近似的视为稀疏信号，因此在接收端使用CS中的正交匹配追踪(Orthogonal Matching Pursuit,OMP)算法来恢复截断产生的失真信号。接收端的CS重建流程如图2所示。

图2 接收端CS重建模块

在接收端衰落信道下，接收信号y(n)经快速傅里叶变换后在频域可以表示为

(12)

式中：H(k)表示频域信道响应，Z(k)表示加性高斯白噪声且方差为2σz(k)2。在信道响应已知和准确同步的前提下，采用信道量化后可以得到

(13)

原始信号X(k)的最大似然估计值(Maximum Likelihood,ML)可以表示为Xe(k)即

(14)

式中：Q表示信号星座点集合。

结合式(12)～(14)写成矩阵形式，可得

(15)

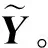
令F=μf，μ为N×N维的单位离散傅里叶变换矩阵，可以得到

η(μf+X-Xe+H-1Z+C)=

ψf+η(X-Xe+H-1Z+C)=

ψf+χ。

(16)

(17)

(18)

(19)

根据最终得到的失真信号，再将其进行消除。TTCSR算法伪代码如下：

1 定义阈值，根据式(1)设置γ。

6 根据式(16)选取可靠的观测值Γ。

8 根据式(17)更新r0=Xfinal(k)。

9 end for

3 数值结果

为了验证TTCSR的适用性，本文在OFDM及W-OFDM系统上完成了仿真测试。仿真时用TT表示经阈值截断处理的信号，TTCSR表示恢复后的信号。阈值γ根据式(3)设置，本文选取l=4处的干扰功率作为式(3)中的β值。OFDM信号的包络服从瑞利分布[16]，截断的概率为e-γ，截断后失真信号的稀疏度K选取为e-γ×N,仿真参数如表2所示。

表2 参数配置

3.1 仿真结果分析

图3比较了OFDM、TT-OFDM以及W-OFDM的PSD。在抑制带外泄露(Out of Band,OOB)方面，相较于OFDM信号，W-OFDM波形具有很好的性能，而本文所采用的信号截断方法即TT-OFDM性能次之。

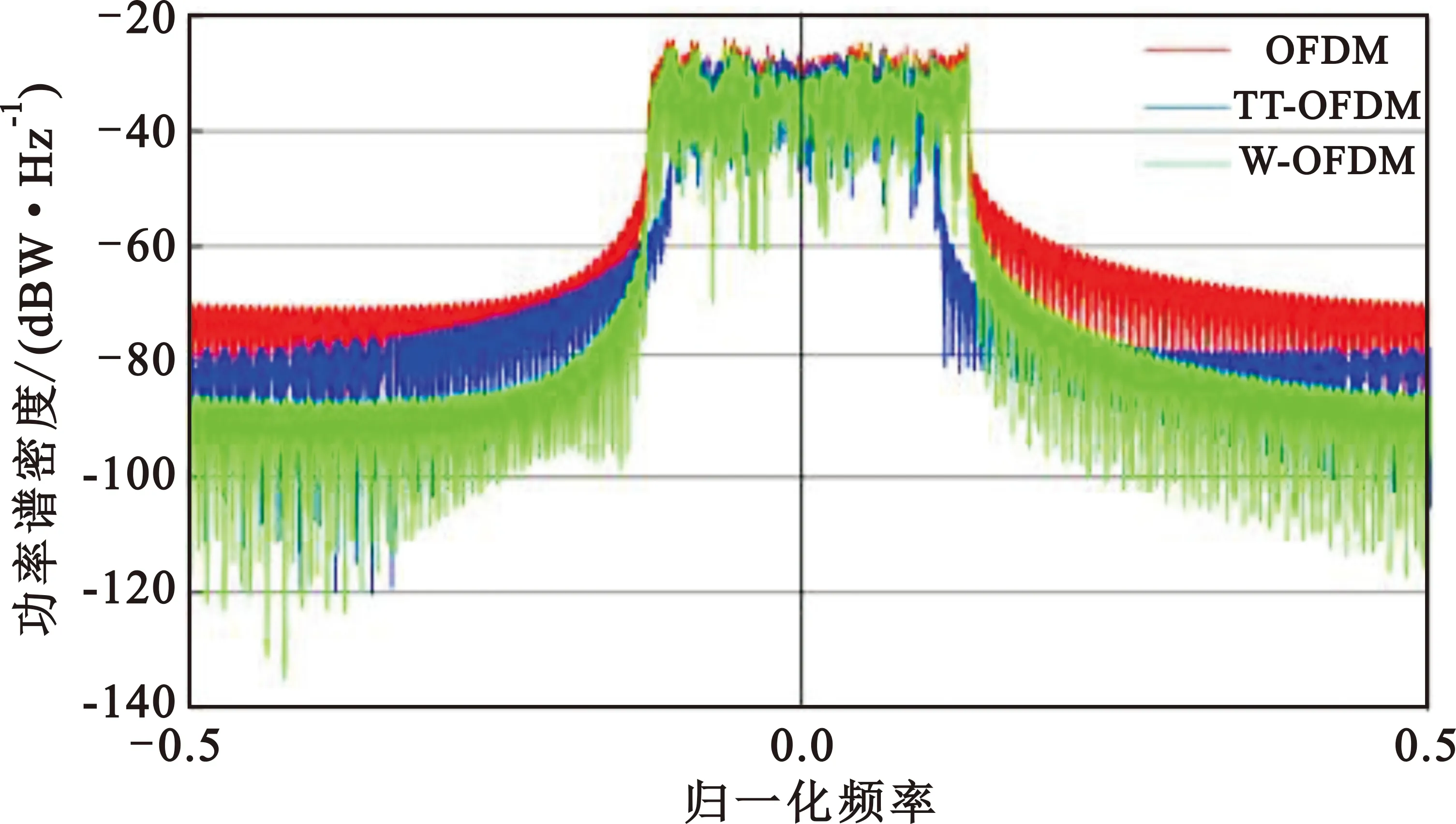
图3 OFDM、TT-OFDM和W-OFDM的PSD对比

图4针对OFDM系统进行了仿真验证。由仿真结果可知，使用TTCSR方法处理明显降低了系统的误码率，系统BER性能得到改善。例如，当信噪比为12 dB时，受到干扰的信号OFDM+ACI的BER为9.10×10-2，截断后的信号TT-OFDM的BER为1.2×10-3，而恢复后的信号TTCSR-OFDM的BER为7.34×10-4，相较于未恢复的信号，系统BER性能得到了改善。

图4 AWGN中TTCSR应用于OFDM系统的BER性能

图5针对W-OFDM系统进行了仿真验证。由仿真结果可得，使用TTCSR恢复的W-OFDM信号有较好的误码率性能。例如，在8 dB和10 dB的情况下，经过TTCSR恢复后的信号对应的误码率分别为1.15×10-2和2.2×10-3，相较未恢复的信号BER性能得到改善。

图5 AWGN中TTCSR应用于W-OFDM系统的BER性能

图6和图7在瑞利信道下对OFDM系统以及W-OFDM系统进行了仿真验证。由仿真结果可知，TTCSR方案在瑞利衰落环境同样能够改善误码率性能。

图6 瑞利信道中TTCSR应用于OFDM系统的BER性能

图7 瑞利信道中TTCSR应用于W-OFDM系统的BER性能

3.2 复杂度分析

本文使用的TTCSR方法,在发送端采用阈值截断，比较简单直接；在接收端主要考虑式(16)中的CS方法。接收端采用OMP算法来恢复式(16)中的稀疏信号，计算复杂度为O(KMN)。因此，本文算法总的复杂度大致可以表示成O(KMN)。

4 结束语

新一代5G无线通信需要更加灵活的资源配置，允许相邻频带中非正交的接入波形。本文针对5G中非正交接入波形共存干扰的问题，提出了TTCSR算法来截断信号并恢复失真将其消除。仿真结果证明TTCSR算法能够很好地消除干扰，并使系统的BER性能得到了很大的改善。本文结果证实了TTCSR方法能够较好地解决OFDM和W-OFDM信号在5G多业务共存中的非正交接入干扰问题。针对5G中其他候选波形，后续工作将继续完成TTCSR方案有效性的验证。