核心素养视角下初中数学复习课教学策略

王荣华

（平潭城关中学，福建 平潭 350400）

数学是培养学生思维的重要学科，初中阶段是发展中学生思维的关键期，教师作为学生发展的促进者，应深刻理解数学核心素养的内涵，结合初中学生的认知特点设置好教学活动，促进数学思维能力的提升。

复习课是初中数学教学中不可或缺的一环，上好复习课，对学生整体把握数学、提高思维水平非常重要。在新课程的背景下，初中数学复习课的教学实践应立足数学学科核心素养，倡导新型教学模式，提升教学效果，提高学生综合素质。本文从核心素养视角，探究初中数学复习课教学的策略。

一、当前初中数学复习课的教学现状

（一）教学目标不明确

当前初中数学的复习课教学，部分教师在理念上仍然无法摆脱应试教育。为了提高学生成绩，有些教师轻知识、重训练，在复习课中采用“题海战术”，对考试相关的试题重复、机械地训练，进行单向灌输讲解，造成复习课没有明确的目标，导致学生基础知识分散，难以形成比较完善的数学知识体系。这种教学方式目标不明确，完全忽略了教育的本质，很难提高学生学习的兴趣，更难提高学生的思维能力和学科素养。

（二）教学模式落后

在核心素养视角下，复习课的教学模式应是多元化的，教学活动开展过程中应突出学生的主体性，应调动学生积极参与数学教学活动的主动性，提升复习课堂的教学效率。但是，当前的复习课教学，由于教师认识上的偏差，过于片面地追求分数，采用灌输式的教学方式进行教学活动。在这种教学模式下，学生被动接受数学知识，导致了学生只会死记硬背、按部就班，不会触类旁通，复习效率低下，数学思维、解题能力固化，数学素养无法得到发展。

二、核心素养视角下初中数学复习课的教学策略

为了解决数学复习课教学中存在的问题，必须对学生进行核心素养的培养。数学学科素养，指的是在数学学习过程中，学生逐步养成的六大能力，分别是直观想象、数学抽象、运算、推理、建模和数据分析等能力。在初中数学复习课中，以问题设计为主，在夯实学生四基的基础上，强化学生的数学抽象、数学推理、数学建模等能力，从而重塑学生的学科素养。

（一）重视归纳，加强知识结构的构建

在传统的复习模式中，整个复习过程都是对以往知识的重复复习，学生在这个学习过程中只能得到一些点状知识，而在数学素养指导下的复习课，重点是培养学生对数学知识的探究，在学习的过程中，运用思维导图来辅助复习，有助于学生将碎片化的数学知识有效地归纳整理，从而使学生建立一个比较完善的数学知识体系［1］。为了提升复习课的教学效果，教师在开展数学复习教学时，通过构建思维导图和知识体系结构，全面提升学生的抽象素养。

例如，在学习了一次函数、反比例函数、二次函数后，由于学生抽象思维能力比较薄弱，对函数概念的理解不够到位，对三个函数模型的认识不够深刻，有时会出现混倄。在上复习课时，有必要对相关的知识点进行归纳、整理和概括，建立三种函数的知识体系结构图（如图1 所示）。

图1

在初中数学的复习教学中，教师通过多媒体技术的合理运用，把有关的数学知识点提炼出来，通过思维导图或者知识结构图的形式加以归纳，可以解决知识碎片化问题。这种教学方式合理运用了信息技术，重建了学生的数学概念、知识体系结构，重塑了学生的思维品质，提升学生的抽象素养。

（二）加强引导，培养学生的数学推理能力

在教学中，教师通过归类找规律的思路，培养学生的数学建模素养。教师要依据实情，指导学生思考和整理有关例题，并从中总结出解题规律。针对可变性题型，要引导学生从不同角度综合分析问题，采用分类法掌握解题方式和思维方式的规律［2］。在复习教学中，数学问题的探究必须在教师引导下进行，通过引导能够培养学生对数学问题探究的兴趣，解决以往复习教学中存在的不足之处。教师在进行初中数学复习课教学时，针对可变性问题的探究，通过加强对学生的引导，强化学生的数学推理能力。

在学习完全等三角形知识后，学生的全等三角形应用比较弱，在复习课教学上，教师要对有关几何证明问题重新进行重新设计，并加强引导。

例如，已知，如图2 所示，△ABC和△DCE都是等腰直角三角形，∠BCA与DCE都是直角，问题：BE和AD是否垂直？有垂直，请加以证明；不垂直，请说明理由。

图2

引导问题：请你画出BE的延长线，交AD于点F，那么，BE和AD具有什么位置关系？

课堂上让学生动手操作，画出BE的延长线交AD于点F，为了引导学生得出BE和AD位置关系，设计以下问题。

问题1：∠BFD等于多少度？测量角度用什么工具？

问题2：在图形中，哪两个三角形有可能全等？这两个三角形全等已经具备了几个条件？还缺条件吗？

在解决完以上问题后，再设延伸性问题继续引导学生对数学问题的探究。

问题3：其他条件不变，把△ABC绕着点C按顺时针方向旋转，有什么结论，请加以解答。

问题4：其他条件不变，把△ABC绕着点C按逆时针方向旋转，有什么结论，请加以解答。

由此可以看出，数学复习中加强教师的引导作用，是非常必要的。引导的方式具有多样性，可以是课堂，也可以是课后。课堂上可以引导学生先复习知识，再对问题进行探究，也可以引导学生先进行问题探究，再进行知识点的复习。课后的数学复习，教师要指导学生阅读数学读物，树立学生的信心，引导学生与教师、其他学生交流，引导学生展示自我。

在数学问题的复习中，为了更好地突出学生的主体地位，通过问题的设计，教师逐步引导学生动手操作、探究问题、拓展延伸，树立学生学数学、用数学的信心，从而提升数学推理能力。

（三）鼓励质疑，提高学生参与度

教学是否精彩，关键在于教师能否运用有技巧的提问，使学生思维浪花涌现出丰富多彩的美丽涟漪。把问题下放给学生，培养学生提出问题的能力，把学生推到“学”的制高点上，才能培养出新世纪的创造型人才［3］。首先要树立起问题意识，学生要学会提出问题，并且能解决自己提出的问题。其次，教师对于学生提出的质疑及解题技巧给予点评，要善于发现学生在课堂活动中的优点并给予肯定，在质疑中培养出探究精神，提高学生参与复习课的积极性与主动性。

在中考复习“二次函数”教学中，课前教师跟学生进行沟通，倾听他们的想法，了解学生存在的问题和不同的疑问。在实战中，教师适当鼓励学生提出心中疑问，并由学生参与共同解决疑问。

例如，如图3，平面直角坐标系中，直线y=+2 分别交x轴、y轴于点A、B，抛物线y=-x2+bx+c经过点A、b。点P是x轴上一个动点，过点P作垂直于x轴的直线，分别交抛物线和直线AB于点E和点F.设点P的横坐标为m。

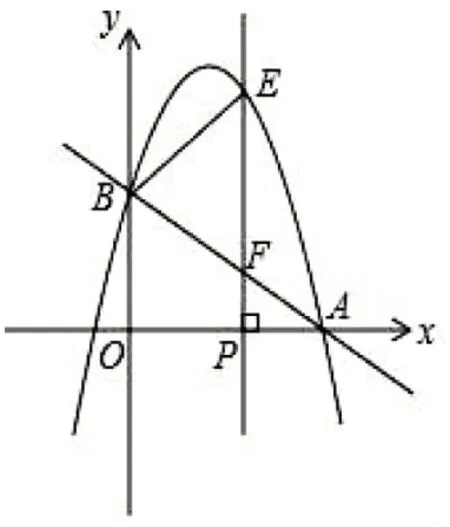
图3

（1）点A的坐标为________；

（2）求这条抛物线所对应的函数表达式；

（3）点P在线段OA上时，若以B、E、F为顶点的三角形与△FPA相似，求m的值；

围绕以上问题的探究，师生、生生之间进行适当的互动，特别是在进行问题（3）的探究时，部分学生会这样考虑问题“∵△BEF和△APF相似，且∠BFE=∠AFP， ∴∠BEF=∠APF=90°，则有BE⊥PE”。由于学生思考问题的方式不周全，教师适时鼓励学生提出疑问“上述解题思路是否妥当？如果不太妥当，应该怎样解题?”，学生答“∵△AEP和△APF相似，且∠BFE=∠AFP，∴∠BEF=∠APF=90°或∠EBF=∠APF=90°”。

从学生的质疑和解析来看，相同条件有两种结果而不是一种结果，这就需要学生在上复习课时，对于数学问题要进行比较深入探究，考虑问题要周到，教师要鼓励学生敢于质疑和解决问题。

在教学中，适时复习知识如“相似三角形的性质有哪些呢？”“一元二次方程的解法有哪些？”等。这是比较典型的中考函数复习题，在对待这类问题的探究时，课堂上需要同学们敢于提出问题，并深入地解决学生所提出的问题。这种鼓励质疑的教学方式，拓展学生的思维，提升学生的参与度，同时变题海战术为针对性训练，突显出学生的主体地位。

因此，在数学问题的探究过程中，教师要适时鼓励学生大胆质疑，课堂上出现了师生互动和生生互动的情景，使得数学课堂重新焕发青春活力。在问题的探究中，学生复习了有关知识和解题技巧，提升了思维品质。采用这种方式进行复习教学，注重培养学生提出问题和解决问题的能力，把学生推到主动学习的制高点上，才能培养出创新型人才。

（四）重视变式，拓展学生的思维

在复习教学中，教师要指导学生思考和整理有关例题或者练习题，并从中总结出解题规律，重构学生的数学模型，拓展学生的思维。

例如，在（三）复习函数知识的问题中，教师要适时进行变形，以强化学生对数学知识的理解，下面是笔者的问题设计。

（1）直线AB的解析式改为y=+b，抛物线改为y=-x2+bx+2，求这两种函数的解析式。

（2）以B、E、F为顶点的三角形与△FPA能全等吗？

（3）连接AE，求四边形AOBE的面积m与x的函数关系式。

（4）四边形AOBE的面积是否能够等于3，6，8，20？等等。

在以上问题的探究中，教师通过复习函数待定系数法模型，适当地进行变式训练，重建学生的待定系数法思想方法。在复习三角形全等或者相似知识点和解题技巧过程中，重构三角形有关知识架构，在复习四边形的面积以及参数求法中，重温学生的面积求法以及面积的拓展延伸应用，结合引导和质疑措施，改变机械训练的题海战术，从而拓展学生的思维，重构学生的知识体系。

在复习教学中，教师必须抓住问题的核心，通过层层递进的问题探究，引导学生多侧面、多角度地思考问题，让学生多探讨、多争论，使得学生的思维品质更具完备性、深刻性和创造性。在这种变式教学的复习中，教师既重塑了学生的思维品质，又培养学生的创新能力。

在核心素养视角下，初中数学复习课的教学方式将发生重大改变。以上复习课所采用的教学策略，有助于教师合理组织教学，有助于教师进一步优化教学方案。教师通过重视归纳、加强引导、鼓励质疑、重视变式等措施，精准地巩固学生的数学知识，合理地重构学生的数学知识体系，有效地重塑学生的思维品质，夯实了学生的基础，突显出学生的主体地位，帮助学生树立起学数学、用数学的信心，从而促进学生的学科素养的养成。