基于学习进阶的中学数学反比例函数教学

范伟

（南平市教师进修学院，福建 南平 354200）

学习进阶以学生为主体，重视培养学生思维方式。在比较大的时间范围内，学生学习某一主题时，思维方法逐次进阶。学习进阶理论是制订中小学数学课程标准的一个重要依据，学科素养背景下，教材编写更加趋向于大任务、大项目的单元设计，教师明确教学要求对落实立德树人、发展学生终身学习能力、深化学科课程改革都是极为重要的。文章结合初中数学函数教学实际，构建基于学生视角的、清晰的学习的“阶”，分析初中数学学习进阶教学策略，提高数学教学效率。

一、用大单元构建教学内容框架

学习进阶的对象是学科中的大概念学习，教师应在充分了解学生知识基础和能力经验的基础上，以认知某一具有知识生长点和延伸点的数学“核心知识”为目的，掌握知识的结构关系，用大单元设计教学内容、组织教学活动，进一步培养学生学会学习、终身学习的数学核心素养。

函数是初中代数的主要内容，包括一次、二次、反比例三类典型的函数。函数学习的精髓和核心是构建函数关系，通过概念、图象和性质，以及使用函数方法来解决问题的思维方式。函数概念引入后，解方程f(x)=0 就变成了求函数y=f(x)的零点，函数与方程思想的引入，提高了对于函数知识的概括能力，利于加强提炼算术关系，该思想在研究数学教学内容过程起着十分重要的作用。反比例函数是我们接触的第一个双曲函数，研究其渐近线、收敛性和图象拐点的方法，是由有限来把握无限的极好例证，对树立学生极限的思想很有意义！

初中阶段从变量的角度研究函数，从函数的角度认识反比例关系，增加了一种函数类型后，特别是对于反比例函数中自变量不能取0 的研究，极大地加深了学生对函数的认识。［1］

二、尊重学生认知发展规律，遵循学习进阶理论

进入九年级以后，学生数学认知水平呈现低起点、高落差、多层次的特点。教师应该结合学生认知情况，分析学生能力，构建更加清晰的“阶”，促使学生能提高思考、预测、反思能力，从而加强数学知识的感悟水平，进阶路径如图1所示。

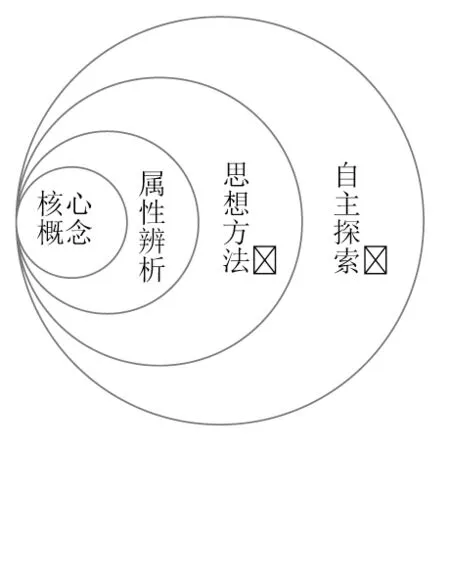
图1 进阶路径

（一）第1 阶：类比一次、二次函数，通过概念学习明确反比例函数的内涵

组织反比例函数教学内容时，结合具有反比例性质的数学模型入手，选取现实世界中的典型实例，举三反一：以典型案例为主，通过分析比较的形式，明确共同本质，加强对函数属性的分析能力；将共同本质属性进行推广，融入同类解题过程，结合反比例关系以及函数概念，引导出反比例函数。

例1.若点p(x0，y0)是双曲线y=k/x图象上任一点，则x0y0=k.

用以解决某些关于面积、极值的问题。

例2.在直角坐标系中，一次函数k1x+b的图象与反比例函数y=k2/x的图象交于A（1，4）、B（4，1）两点，则△AOB的面积是______.［2］

【设计意图】利用反比例函数、一次函数图象与性质解决相关问题，渗透图象法、数形结合等数学思想方法.

（二）第2 阶：分类讨论，掌握反比例函数的性质

把握方向，以本为本，自然延续使用教材中的练习、习题。教材习题具有多重功能：“复习巩固”层次的习题以基础知识为主，旨在加强学生基本技能；［3］“综合运用”层次的习题以分析知识间的联系为主，旨在加强学生综合运用水平，促使学生能运用知识点解决问题；“拓广探索”层次的习题更加具备实践性，利于学生发挥，从而让学生都能上手，促进不同学生得到不同的发展。在反比例函数教学中，我们在概念的基础上，数形结合，通过解析式，得出其图象，分类讨论k＞0 和k＜0 的情形，研究其性质，运用性质解决一些具体问题。

例3：如图2，直线l 与双曲线交于A、C两点，将直线l 绕点O 顺时针旋转a 度角（0°＜a≤45°），与双曲线交于B、D两点，则四边形ABCD的形状一定是___.［4］

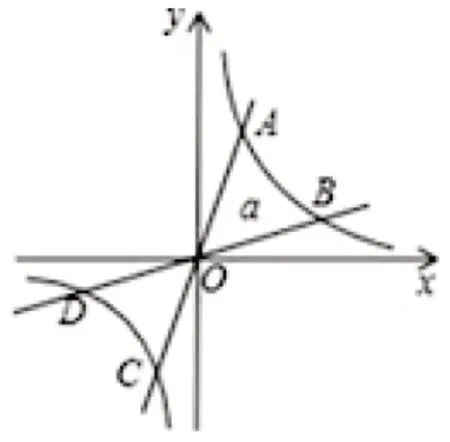
图2

【设计意图】复习反比例函数的性质，渗透分类讨论思想.

例4：在平面直角坐标系xOy中，△ABC的顶点A（4，2），C（4，0），B（3，0），反比例函数y=k/x（k＞0）的图象过AC的中点D.

（1）求反比例函数表达式；

（2）已知点B关于点E（2，2）的对称点F，试判断点F是否在反比例函数的图象上，并说明理由.

【设计意图】以函数图像为呈现方式，复习函数的关系式的确定、图象法，并体现函数与几何的关系。

（三）第3 阶：用运动变化的观点，确定反比例函数渐近线

当曲线上一点F沿曲线无限接近间断点时，F到某一条直线的距离无限趋近于零，这条直线称为这条曲线的渐近线。对于这种特征，我们称为收敛。反比例函数图象既是轴对称图形，又是中心对称图形，除了有对称中心，直线y=x和y=-x两条对称轴外，还有两条渐近线。结合分式的性质，通过间断点的判断，从不同方向逼近，确定水平渐近线、垂直渐近线。学生掌握这种思想，对今后学习双勾曲线和圆锥曲线大有裨益。

（四）第4 阶：自主探究反比例函数隐藏的结论

教材在每一章都设置了探究性、开放性的“数学活动”，在教学过程中，教师要结合学习内容，科学地对这些数学活动进行指导，使学生在参与过程中，加强对本章知识点的掌握，提高实践水平。学生通过主动思考、交流提高了自主探索能力，加强了对于数学知识的运用水平。

在初三阶段，学生要学会挖掘反比例函数隐藏的结论，体会其中蕴含的数学价值。作为历年中考必考点还体现数学知识的综合性、渗透性、迁移性、指导性，其解题难度超过了课本例题的能力要求。

例5:点A、B是双曲线y=k/x（k≠0）任意不重合的两点，直线AB交y轴于C点，交x轴于B点，再过A、B两点分别作x轴垂线于E点，y轴垂线于F点，再连接DF两点，则有：AC=BD且AB∥EF，CD∥EF.

例6：菱形ABCD顶点A在函数y=3/x（x＞0）的图象上，函数y=k/x（k＞3，x＞0）的图象关于直线AC对称，且经过点B、D两点，若AB=2，∠BAD=30°，则k=___.

【设计意图】复习反比例函数和一次函数有关知识，复习函数图象上点的坐标与函数的关系，同时复习图象法，体现函数与几何的有机结合，灵活应用反比例函数图象解决问题。

三、注重培养学生高阶思维方式

从学生的立场引领学生经历基本的科学实践。在引入坐标系的基础上，以动画的形式，用形来研究数的问题，用直观的视觉表征的方式呈现反比例函数的图象，帮助学生化解难点，增进学生对问题的认识，培养高阶思维方式。同时能培养学生的直观想象、逻辑推理等数学核心素养。

在反比例函数教学中，基于学习进阶，狠抓基础，注重过程，渗透思想，突出能力，强调应用，着重创新，整体把握单元结构，开展和推进项目化学习。从学科核心素养的高度审视大单元结构，以起统率作用的大概念、大项目为依据进行单元的整体教学设计，将概念模型建构与单元结构有机统一，利于提高学校科学教育质量，推动学课程建设的健康发展。