融入数学文化 助推学科核心素养落地

刘丽丽

（厦门市金尚中学，福建 厦门 363100）

2019 年7 月，中共中央、国务院在《关于深化教育教学改革全面提高义务教育质量的意见》中明确指出，实施“五育并举”是发展素质教育的基本途径。“五育”中的德育是素质教育的灵魂。当前学校德育工作不再止步于道法课堂和班主任的班会课堂，各学科教师都应寓德育于学科教学中。而基于学科特点找到学科教学和德育工作的融合点，使学生在提高学科素养的同时德育素养也能扎实落地，这无疑对教师的教育教学能力提出了更高要求［1］。以下笔者将结合数学学科特点及初中学生特点，提出将数学文化融入初中数学教学实践中，挖掘数学文化中的德育价值，并将其渗透在数学知识的教学中，从而实现学科德、智育双落地。

一、以数学文化为渗透点的教学实践研究

数学文化不仅是狭义理解的数学史和数学家故事，还包括数学发展中的人文精神、数学思想方法、数学与社会、数学与各种文化的关系等［2］。因此，数学文化是寓德育于数学课堂的重要载体。下面笔者结合教学案例，尝试将数学文化融入新知生成、习题命制与讲评及布置课后作业三个教学环节。

（一）数学文化融入新知生成

当前初中数学教学中，多数教师更重视运用知识进行解题的教学，而忽视了知识产生发展的过程，使学生对所学知识“知其然而不知其所以然”，导致在应用时经常概念混淆不清，无法顺利解题。因此教师在教学时应重视知识的生成过程，通过挖掘知识产生的源头背景，还原其发展过程，让学生学习既有源头又有流向的数学知识。这不仅能促进学生对知识本质的理解，也能让学生从中受到数学文化的熏陶。

［案例1］一元一次方程概念

人教版教材将一元一次方程编排在七年级上册，由此拉开了初中段学生对方程学习的大幕。万事开头难，学生对一元一次方程概念的理解与掌握，直接影响后续对二元一次方程（组）、分式方程、一元二次方程的学习。为此笔者在讲授这节课时，将重点放在让学生理解“元”与“方程”的含义上，提前让学生搜集方程产生与发展的相关数学史料，课堂上以方程的发展史为切入口：

师：同学们，昨天你们已经搜集了与方程相关数学史料，我国古代研究方程的著作有哪些？

生：有《九章算术》《张丘建算经》。

师：是的，我国古代对方程的研究的著作很多，可以追溯到成书于公元前200 年的《九章算术》第八卷，这一卷即名“方程”。“方”意思是并列，“程”意思是用算筹表示竖式。哪位同学可以介绍一下“元”的由来？

生：李治在《测圆海镜》中，用术语“立天元一”表示“设未知数x”。

师：是的，宋元时期，中国数学家创立了“天元术”，用“天元”表示未知数而建立方程。同学们，不仅我国古代数学家对方程很有兴趣，西方的数学家也深深被方程所吸引，你们搜集到了国外早期研究方程的著作吗？

生：西方对方程最早的研究记录在820 年左右的《对消与还原》这本书中。

师：这比我国数学家对方程的研究晚了近一个世纪。教材中对一元一次方程的定义是“只含有一个未知数（元），未知数的次数都是1，等号两边都是整式，这样的方程叫作一元一次方程。”这恰恰是沿用了我国古代对方程及未知数（元）的表述。下学期我们将学习这样的方程：x+3y=5，哪位同学可以给这个方称命名？

生：这是二元一次方程。

师：非常好，看来你已经理解了“元”和“方程”的意义了。

1.学科价值

学生对方程的学习贯穿于整个初中阶段，以人教版教材的编排为例，七年级上学习一元一次方程、二元一次方程（组），八年级学习分式方程，九年级学习一元二次方程。融入方程发展史料讲解一元一次方程概念，让学生学习有源头，有流向的一元一次方程概念，既能帮助七年级的学生精准解读一元一次方程概念的本质，同时有助力于后续方程学习。

2.德育价值

初中教材中多数数学概念、数学符号都是由西方引入。由于我国古代数学家较早研究并引入方程解决实际问题，故一元一次方程概念是沿用我国古代的表述来命名，这是中华民族的骄傲。课堂上通过讲述方程发展史，让学生了解祖国的传统文化，震撼于其博大精深，同时培养学生的民族自豪感。

（二）数学文化融入习题命制与讲评

纵观2020 年全国各地的中考数学试卷，发现各地的试卷中都有文化类试题。特别是福建省近四年的数学中考试卷中均出现选自我国古代数学名著的题目。命制有数学文化背景的题目，不仅具有考查学生数学知识的功能，还体现了立德树人的教育导向。

［案例2］用“海伦—秦九韶公式”设计课堂习题

在学生学习二次根式加减这节课时，笔者结合教材（人教版八年级下册）在章末阅读思考中介绍的海伦-秦九韶公式，在原材料基础上设计改编了一个材料阅读题如下：

几何学的产生源于古人测量土地面积。三角形是最简单的平面几何图形。古希腊数学家海伦以解决几何测量问题而闻名，他在《度量》一书中给出了已知三角形三边长求三角形面积的公式——海伦公式：

若一个三角形的边长为a，b，c记p=，则三角形的面积为S=。

我国南宋时期的数学家秦九韶也提出利用三角形的三边长求面积的秦九韶公式：

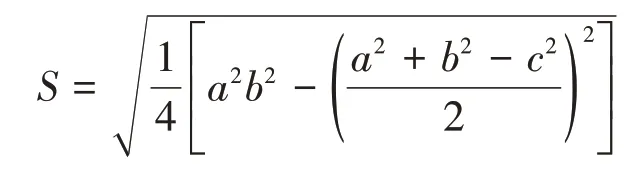
请根据以上材料解决下列问题：

（1）若三角形的三边长分别为4，5，6，请选择一个公式计算出三角形的面积。

解析：（1）选择海伦公式或秦九韶公式的同学都可以通过计算得出：S=.

（2）选择海伦公式的同学会陷入繁琐的计算并两次运用平方差公式来简化计算：S==2.

选择秦九韶公式的同学相对就顺利了很多：S==2.

1.学科价值

问题（1）是考查学生阅读材料提取信息，并应用所学的二次根式的计算法则选择材料中所提供的两个公式之一解决问题。问题（2）并不是多余重复，实则考查学生鉴别并甄选出适合这组数据的公式。学生通过计算，教师再引导学生观察两个公式的结构特征会发现：海伦公式采用了换元法，记p=，使公式更简捷，但当三角形边长出现二次根式时，计算量很大且需要运用技巧简化计算。秦九韶公式形式上比海伦公式略显烦琐，但计算量小，实用性更强。通过这两个题目，学生不仅巩固练习二次根式的加减乘除运算，同时学会观察代数式结构，甄选方法的解题策略。

2.德育价值

通过运用两个公式求解三角形的面积，让学生体会“数学来源于生活，服务于生活”，震撼于古今中外劳动人民的智慧，从而激发学生的学习兴趣。

（三）布置有文化韵味的课后实践作业

“纸上得来终觉浅，绝知此事要躬行。”要让学生真正理解书本上的知识，亲自动手操作是必要的。受课堂时间和空间的限制，动手操作型问题的探索往往不够完整深入。课后作业是教师课内教学的延伸，同时是学生巩固理解课内知识的重要途径。课后学生不再受限于空间和时间，布置一些数学发展史上的经典数学实验，既能培养学生的动手能力，同时能让学生在试验中感受数学家们锲而不舍的求真精神。

［案例3］用频率估计概率

初学概率的学生容易混淆概率和频率这两个概念，更难理解两者的联系与区别。为此笔者在讲授这节课时，在课堂上采用学生分组试验掷一枚质地均匀的硬币，统计结果中“正面朝上”的频率，但课堂时间有限，学生不能大量重复实验，统计出来的结果与理论值0.5 偏差稍大。为体现频率的规律，笔者介绍了几位历史上做过这个实验的数学家并将他们的实验结果展示给学生（如表1 所示）：

表1

观察表1，学生从数学家们的实验结果中不难发现“正面朝上”的频率随实验次数的增加会越来越稳定在0.5 附近。由此得出可以通过大量的重复实验，用一个随机事件发生的频率去估计它的概率。但这一结论的得出，并非学生亲自经历大量重复试验所得，而是从科学家的实验结果中去总结，这对学生理解用频率估计概率的必要性产生了影响。为弥补这个缺憾笔者将“抛掷图钉求‘顶尖朝上’的概率”布置为课后作业，旨在让学生通过大量实验，理解频率与概率两者之间的联系及用频率估计概率的意义。具体设计如表2：

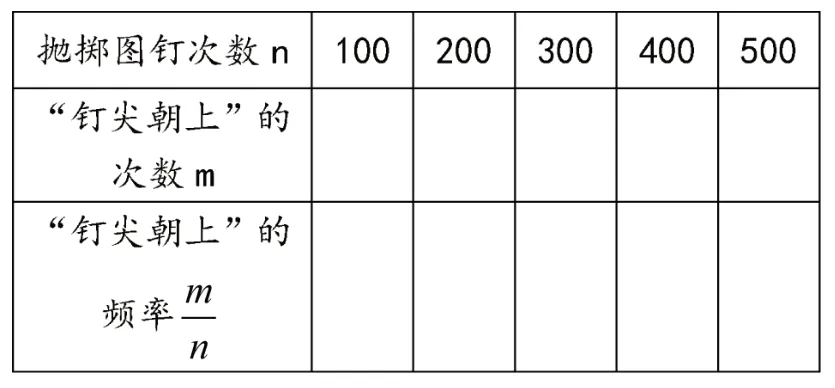
表2

抛掷图钉试验（改编“布丰投针”实验）：

1.抛掷一枚图钉，整理获得的实验数据并完成表2。

2.通过观察分析上表中的数据，请估计“钉尖朝上”的概率。

3.为提高“钉尖朝上”的概率的估计精度，在试验中你认为有哪些注意事项？

4.你能否根据上述试验的设计思路，设计一个实验求这个不规则图形的面积？（图1）

图1

1.学科价值

课堂上抛掷硬币实验因时间限制并不充分，并未呈现出明显的规律，学生对用频率估计概率的必要性并不能理解。这个课后作业恰是对课堂的延伸，让学生通过自己做试验统计数据并观察得出频率与概率的关系。让学生理解概率和频率的区别与练习，积累活动经验，并学会用频率估计频率的方法解决实际问题。

2.德育价值

通过学生亲自动手，体会科学家们在大量重复实验中探求真理的顽强精神，培养实事求是的科学探索精神。

二、数学文化融入教学的建议

（一）找准数学文化在课堂教学中的渗透点

并不是每节数学课都适合渗透数学文化，在课堂教学中找到数学文化的渗透点，才能做到有的放矢［3］。教师自身文化素养高，在课堂教学中对相关知识的来龙去脉可以信手拈来固然好，但数学文化积累深厚的一线初中数学教师并不多，知晓讲解哪些知识时可以融入文化就显得尤为重要。教材及教师教学用书中，每一章都有相关与本章中重点知识或概念的数学史背景介绍，或是本章知识在其他领域的应用介绍。教师在备课中充分运用这些素材进行加工整理，在课堂教学中浸润数学文化就游刃有余了。由此可见，章节起始课及重点概念的教学即是数学文化的有效渗透点。

（二）数学文化在课堂教学中呈现形式应多样化

课堂上少用教师口述讲授数学史、数学家故事，学生被动接受的形式。现在是多媒体时代，教师布置主题明确的作业，学生便可以很快捷地利用网络或在图书馆查阅到相关的历史材料。教师应大胆放手，让学生课前搜集与所学知识相关的数学史料并加工整理，课堂上以学生讲数学家故事、播放相关史料视频、表演历史剧等多种形式来介绍相关数学知识。课堂教学中多样化呈现数学文化，既符合现在初中生的心理特征，同时学生全程参与搜集并展示整个过程，更易于学生理解数学知识及其文化背景。

（三）重视拓展文化类题目外延

文化类试题的讲解很关键，精讲一题可以让学生了解一个时期古代数学发展概况及其相关的数学文化。学生往往只能体会题目中直接呈现出的背景情境，而题目内在的数学思想方法及其承载的同时期的古代文化则需要教师娓娓道来。例如，讲解出自《九章算术》的题目时，可以向学生介绍《九章算术》的作者、成书背景以及当时我国数学的发展状况等，充分挖掘题目所蕴含的文化素材，由一题目让学生了解一个时期的数学文化。

（四）寓德育于“润物细无声”中

在文化渗透中对学生进行德育不应太生硬，这样会给学生造成一种“为德育而文化之”的不适感，德育效果也会大打折扣。要让数学文化“随数学知识潜入课堂，德育学生于无形中”，这样的课堂才是高效的。数学文化的引入既加深学生对数学知识的理解掌握，同时让学生在文化滋养中了解数学发展概况、领悟数学思想方法并震撼于数学家拼搏进取的精神及我国传统数学文化的博大精深。这样的融入才是自然的，真正的“一举两得”，实现了学科德智育双落地。