一种基于对角积分双谱的复合调制LPI雷达信号识别方法*

孟祥豪，赵海旭，梁 言

（1.国防科技大学，安徽 合肥230037；2.陆军炮兵防空兵学院，安徽 合肥230037）

0 引言

雷达辐射源信号识别是雷达侦察系统的重要环节，通过雷达辐射源信号识别，结合一定的情报分析，可以判断敌方发射该信号的辐射源，并进一步得出搭载该辐射源的载体及敌方的武器威胁等级等。因此，雷达辐射源信号识别在雷达侦察中具有十分重要的地位和作用。传统的识别理论利用脉冲雷达信号的“五大参数”，同时综合天线扫描样式、功率参数、时域频域波形等特征，可推断出雷达的体制、用途、平台以及威胁等级等信息。但随着科技的发展，传统方法已经不适用于对LPI雷达的侦察与截获。因此，本文采用基于高阶统计量的分析方法，主要针对LFM、BPSK、FSK、LFM-BPSK复合调制信号和FSK-PSK复合调制信号，采用双谱估计的方法对信号进行特征提取，并利用对角积分双谱对数据进行降维处理，进而利用其双谱特征进行调制类型识别。

1 LPI雷达信号建模与分析

由于LFM、BPSK、FSK等单一调制信号在前人的研究中都已经被详细介绍过，因此，本文在这里不再进行过多赘述。下面主要介绍本文所采用的复合调制LPI雷达信号的建模与分析。

1.1 LFM⁃BPSK复合调制信号建模与分析

LFM-BPSK信号是LFM信号与BPSK信号混合的信号，其克服了BPSK信号对多普勒频移敏感的缺点而且具有良好的距离分辨率和速度分辨率。LFM-BPSK信号是对信号频率进行线性调制的同时对相位进行数字调制。LFM-BPSK信号的表达式为：

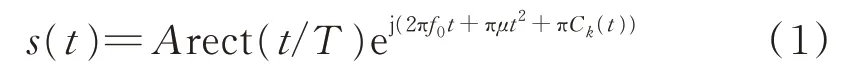
式中，μ为调频斜率，C k(t)为相位编码函数。其离散形式的信号模型为：

式中，f0为信号载频；k为调频系数；Δt为采样间隔；θ(n)=πd2(n)为相位编码,一般为二元相位编码，故d2(n)∈{0,1};A为信号幅度。也可以根据LFM信号与BPSK信号的特点，结合2种信号的时域表达式，将信号模型表示为：

式中，τ为信号脉冲宽度，N为码元个数，μ为调频斜率，C k为编码序列，T为子脉冲宽度，V(t)为子脉冲函数。

根据信号模型，实现了对该调制类型信号的仿真实现。设置信号的参数为:载频为100 MHz,调频斜率为300 Hz/μs，BPSK采用13位Barker码，码元宽度为0.04/μs。

1.2 FSK-PSK复合调制信号建模与分析

FSK-PSK信号同时具备FSK信号与PSK信号的变化特点。FSK-PSK复合调制信号具有比FSK信号和PSK信号更大的时间带宽积，而且其低截获概率特性更好，对噪声的抵抗能力更强。同时，信号具有良好的距离和速度分辨率，相对于单一的频率编码信号或相位编码信号，其低截获性能也有了较大提高。FSK-PSK复合调制信号主要有在相位编码调制的基础进行载频跳变键控调制和在频移键控的基础上进行相位编码调制2种调制样式。本文主要研究第2种，且相位编码为BPSK。

FSK-BPSK信号的表达式为：

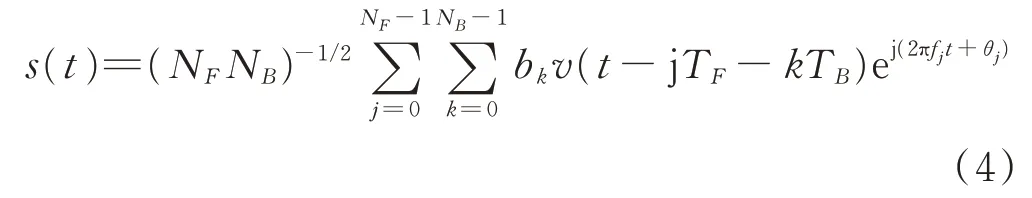
图1 LFM-BPSK信号

式中，v(t)=T B-1/2rect(t/T B)为子脉冲函数，N B为伪随机序列位数，b k为二进制伪随机序列，N F为跳频序列位数，T F=N F T B为跳频周期，f j=c jΔf为跳频频率，c j为跳频序列,T B为码元宽度，Δf为倍频分量，θj为初始相位。

FSK-PSK复合调制信号的频谱表达式为：

{f1,f2,…,fL}为FSK的频率编码；L为正整数；t F为每个频率编码码元宽度；Δt为采样间隔；A为信号幅度；θ(n)=πd2(n)为二元相位编码,且d2(n)∈{0,1}。

根据信号模型，利用Matlab对FSK-BPSK复合调制信号进行仿真。设置信号的参数为：4个载频分别为90 MHz、95 MHz、100 MHz、105 MHz,二相编码采用13位Barker码，码元宽度为0.04/μs。

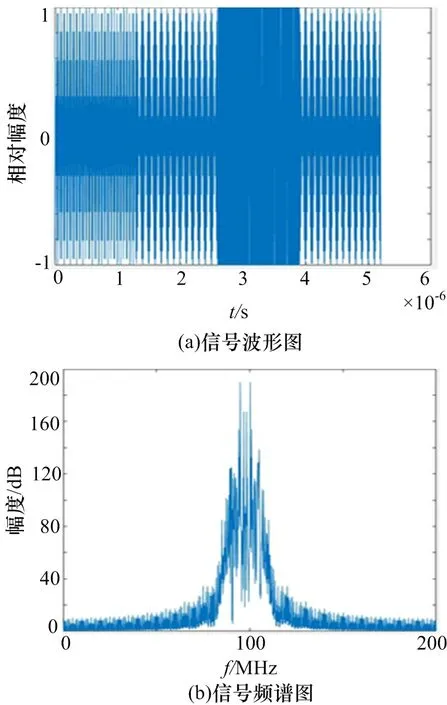
图2 FSK-BPSK信号

2 基于双谱特征的LPI雷达信号识别方法

信号特征是LPI雷达信号识别和分析的基础，一个能够准确反映LPI雷达信号信息的信号特征能够极大地提高对LPI雷达信号的识别准确率。雷达信号特征的提取和选择是信号识别的2个主要过程。高阶累积量的方法在这方面具有明显优点。在使用高阶累积量对噪声进行计算时，其3阶及以上的高阶累积量为0。所以高阶累积量可以大大减少高斯噪声对信号提取过程中带来的不良影响。此外，高阶累积量除了包含信号幅度信息外，其还具有功率谱和相关函数等二阶统计量无法保留的相位信息。因此，本文使用了基于高阶累积量的双谱特征作为对LPI雷达信号的提取特征。同时为了解决得到的双谱数据量比较大不便于计算的问题，使用了将得到的双谱沿平行于对角线的路径积分的方法，得到了相应LPI雷达信号的对角积分双谱。将其作为LPI雷达信号的特征放入线性SVM分类器用来识别LPI雷达信号，并得到不同LPI雷达信号的识别准确率。

2.1 高阶累积量

设函数f(x)的自变量为x，x为连续型随机变量，f(x)的概率密度函数为p(x)，则x的第一特征函数可以表示为：

函数的第一特征函数是由p(x)进行逆傅里叶变换得到。其k阶导数为：

x的第二特征函数由第一特征函数φ(ω)取对数得到，即ψ(ω)=lnφ(ω)。

同理随机变量x的k阶累积量为对第二特征函数ψ(ω)求k阶导数在ω=0时的取值，即：

通过计算，均值为μ、方差为σ2的高斯信号满足c1=μ，c2=σ2，ck=0(k≥3)，因此对于高斯信号来说其3阶和3阶以上的累积量均为零。所以，通过求高阶累积量的方法可以极大地减少噪声对计算的影响。使用该方法在信噪比较低的条件下提取信号的信息有很大的优势。

2.2 双谱特征

k阶累积量的k-1阶傅里叶变换为k阶累积量谱，而双谱是对三阶累积量进行2D-FFT处理得到的。设平稳随机信号为s(t)，时延分别为τ1、τ2，则3阶累积量可表示为：

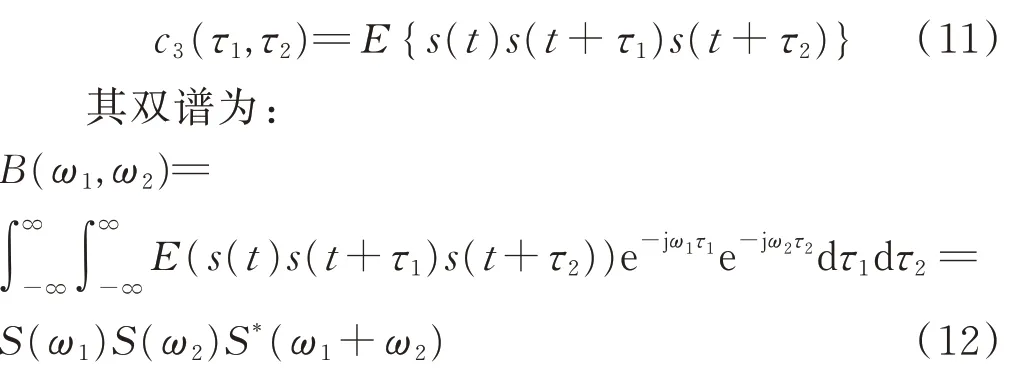
双谱具有以下性质：

1）双谱一般为复数，即：

式中,φB(ω1,ω2)代表双谱的相位，|B x(ω1,ω2)|代表双谱的幅度。通过该式可以分析出信号的相位信息和幅度信息在双谱中仍存在。

2）双谱具有2个周期(周期为2π）。其为双周期函数，其表达式为：

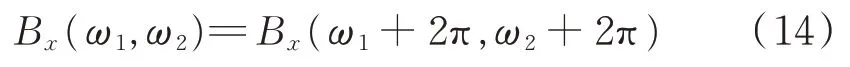
图3为双谱对称性示意图，由(14)式可以得出其取值范围是图中的菱形区域。双谱的频率取值范围为：-π＜ω1≤π，-π＜ω1≤π,-π＜ω1+ω2≤2π。

图3 双谱对称性示意图

3）双谱具有如下对称性：

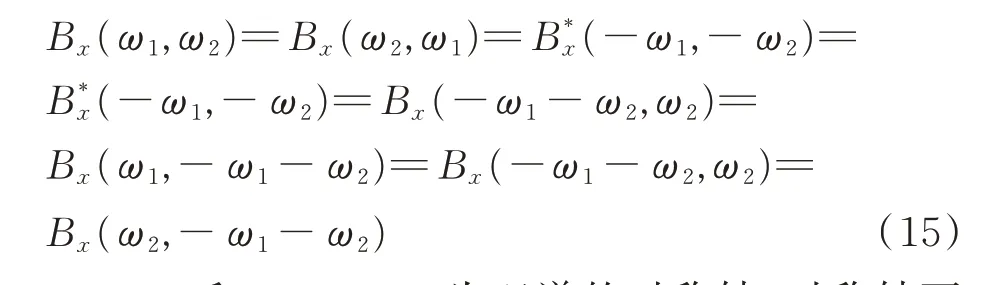
ω1=ω2和ω1=-ω2为双谱的对称轴，对称轴两侧为对称区间。通过观察可以看到双谱可以被分成12个具有相同信息的扇形区域。

根据定义，可以看出双谱是周期为2π的双周期函数。目前对于双谱的计算主要有2种：一种是先对分段数据进行DFT变换，然后求系数的三重相关函数，再取平均；另一种是先对分段的数据求3阶累积量，然后取平均值，最后进行2D-DFT变换。

本文使用第一种方法对BPSK信号、LFM信号、FSK信号、LFM-BPSK和FSK-BPSK信号5种低截获概率雷达信号进行双谱估计，其具体过程如下：

步骤一：将信号分为K段，分段时不重叠，每段分为N个部分，记为s i(0)，s i(1)，s i(2)，…,s i(N-1)，i=1,2,…,K。

步骤二：对步骤一得到的分段数据进行DFT变换：

式中，λ1=max(0,-τ1,-τ2)，λ2=min(N-1,N-1-τ1,N-1-τ2)。

对3阶累积量求和取平均得：

步骤三：对步骤二而得到的数据求3重相关函数，之后在对其求和取平均。

式中,Δ=f s/M0,f s是采样频率，0≤λ2≤λ1，λ1+λ2≤f s/2，N=（2L1+1）M0。

取平均得到信号的双谱估计B(ω1,ω2)：

2.3 对角积分双谱特征提取

由(12)式得到的双谱是二维数据，在实际计算中具有较大的数据量，不便于对其进行数据分析，因此需要对其得到的双谱进行特征提取，来降低信号识别所需要的数据量。

为了解决对双谱的二维数据进行降维处理的问题，本文对得到的二维双谱数据沿着其主次对角线的进行积分。该方法被称为对角积分双谱特征提取，其表达式为：

图4分别显示了主对角双谱积分路径和次对角积分双谱积分路径，分别为式（18）中的S1(θ)和式（19）中的S2(θ)。这2种双谱都是对角积分双谱。

图4 对角积分双谱积分路径

通过2.2节分析双谱的性质可以知道双谱具有12个包含信息完全相同的扇形区域。因此只对其中某一个区域进行分析，通过该区域可得到剩余区域的信息。通过观察图4可以发现，双谱图像具有2个对称轴分别为ω1=ω2和ω1=-ω2。而且如果对扇形A、B、C同时进行积分处理的话，得到的结果将会具有比对单个区域分析更加精确的幅度信息。因此如图4所示在特征提取时仅对实线区域进行计算。

2.4 算法实现步骤

综上所述，基于对角积分双谱的LPI雷达信号识别方法的实现步骤如下：

1）双谱特征提取。针对采样得到的LPI雷达信号，计算其高阶累积量并得到双谱数据。

2）降维处理。对得到的LPI雷达信号双谱特征矩阵主对角线值进行积分，得到降维后的对角积分双谱数据。

3）分类识别。将降维后的数据输入到SVM线性分类器，实现对不同调制LPI雷达信号的分类识别。

3 计算机仿真实验

3.1 算法仿真实现

1）计算信号的双谱

图5为使用直接法双谱估计对5种调制类型的LPI雷达信号在无噪声条件下提取双谱特征的仿真结果。图中展示了5个信号的双谱图展。左边依次为5种调制类型的LPI雷达信号的双谱等高线图，右边依次为5种调制类型的LPI雷达信号的三维网格图。其中，各类调制信号的载频、脉宽等参数设置为：LFM信号的载频为100 MHz，调制带宽为200 MHz，脉宽为10μs，调频系数为20 MHz/μs；BPSK信号采用的是13位Barker码，码元宽度为0.04/μs；FSK信号的载 频分别为90 MHz、95 MHz、100 MHz、105 MHz；LFM-BPSK信号的载频为100 MHz,调频系数为300 Hz/μs，使用13位Barker码进行编码，码元宽度为0.04/μs；FSK-BPSK复合调制信号采用4个载频，分别为90 MHz、95 MHz、100 MHz、105 MHz,BPSK采用13位Barker码，码元宽度为0.04/μs。

图5 各类LPI雷达信号双谱特征图

从5种不同调制类型的LPI雷达信号双谱的等高线图和三维网格图中可以清晰地观察出，上述信号在无噪声条件下的双谱特征各不相同。主要表现为5种不同调制类型的LPI雷达信号的双谱图像的谱峰的峰值、大小、形状和位置都具有很大差异。因此，对LPI雷达信号进行双谱特征提取并识别是可行的。

2）提取各信号特征

通过查阅文献得知，双谱沿次对角线积分计算的双谱包含更多的信息。因此，本文采用该方法来对各个LPI雷达信号的信号特征进行提取。图6为各类LPI雷达信号对角积分双谱特征图。

图6 各类LPI雷达信号对角积分双谱特征图

如图6所示，LFM信号的对角积分双谱与其它的差异最大。BPSK信号、LFM-BPSK和FSK-BPSK信号的对角积分双谱都有数个波峰，存在一定的相似性。但综合观察这5种LPI雷达信号通过沿平行于次对角线的路径积分所得到的次对角线积分双谱特征差别都比较明显。

3.2 算法性能分析

本文通过对算法识别准确率进行统计计算，分析算法的识别性能。

参数设置如下：在高斯白噪声条件下，假定信噪比分别为-5、0、5、10、15和20 d B，对上述5种LPI雷达信号采用间接法得到双谱并通过积分对5种LPI雷达信号的双谱进行降维，之后使用线性SVM分类器对雷达进行识别。使用Matlab仿真软件对每个LPI雷达信号分别在信噪比为-5 dB、0 d B、5 d B、10 d B、15 d B、20 dB时进行50次仿真实验。分类器的训练数据为每个LPI雷达信号在某一信噪比下的前10个数据，测试数据为该信号在同一信噪比下的后40个数据。图7所示为每种类型信号的识别成功率变化曲线。

图7 对于5种LPI雷达信号的识别准确率曲线图

将5种LPI雷达信号通过沿平行于次对角线的路径积分所得到的次对角线积分双谱特征输入到线性SVM分类器中，得到5种LPI雷达信号的识别准确率。通过分析LPI雷达信号双谱的识别准确率图像，可以看出对LFM信号的识别准确率最高，对FSK-BPSK和LFM-BPSK的识别准确率一般，对BPSK信号识别准确率最低。但随着信号与噪声功率之比的增大，其识别准确率也在增大。当信噪比达到10 d B时，5种LPI雷达信号识别准确率几乎都达到了100%。当信噪比继续增强时，几乎能无差错地将不同LPI雷达信号识别出来。

综上所述，利用对角积分双谱特征对LPI雷达信号进行调制类型的识别有较高的准确率，能够提高识别系统抗干扰能力。

4 结束语

本文研究了基于高阶累积量的LPI雷达信号双谱特征提取方法。首先证明了高阶累积量方法在抑制高斯噪声产生的不良影响时作用显著，并介绍了5种典型的LPI雷达信号，通过建立信号模型绘制上述LPI雷达信号的双道图,从得出的双谱图中可以看出不同调制的LPI雷达信景双谱特征各不相同，可以作为不同雷达信号的区别特征，对LPI雷达信号进行识别。然后,针对双谱数据具有较大数据量而不便于对其进行数据分析的问题，对得到的双谱进行降维处理，沿其主次对角线的进行积分。最后，通过仿真实验，证明利用对角积分双谱特征对LPI雷达信号进行调制类型的识别具有较高的准确率，验证了本文所提方法的可行性。