基于阿波罗尼奥斯圆的无人机追逃问题研究

张澄安，邓 文，王李瑞，龙 淼，姚怡舟

（1.国防科技大学电子科学学院CEMEE国家重点实验，湖南长沙410073；2.中国人民解放军75836部队，广东 广州510036）

0 引言

无人机具有低成本、无人员伤亡、操作方便、灵活可靠等优点，近年来发展迅速，结合日益发展的网络信息技术，无人机协同作业表现出巨大的应用潜力，尤其是在军事应用领域[1]。对无人机的追逃问题进行研究，是现代无人机作战的基本要求，具有重要的意义。通常，对于追捕无人机速度大于逃跑无人机的情况，只要时间足够，追捕无人机一定能够截获逃跑无人机，研究的内容在于追捕时间和追捕空间等[2-6]。但对于追捕无人机速度小于逃跑无人机的情况，则存在一个策略选择的问题：对于追捕无人机，采用某种策略，才能最大可能截获无人机；对于逃跑无人机，采用某种策略或某种条件下，一定能够成功逃逸。本文基于阿波罗尼奥斯圆相关定理[7-8]，研究在追捕无人机的追捕速度小于逃跑无人机的情况下无人机的追逃问题，并通过仿真实验，构建追逃场景，验证所构建模型的正确性和有效性。

1 2个单无人机追逃模型构建

本节应用阿波罗尼奥斯圆原理完成2个单无人机追逃模型的建立。首先对阿波罗尼奥斯圆进行描述，阿波罗尼奥斯圆又称为阿氏圆，如图1所示[7]，已知平面上2点P、E，则对于平面上所有满足k,k≠1的点P，其轨迹是一个圆，这个圆就称为阿氏圆。

图1 阿波罗尼奥斯圆

其中点C与点D分别为阿氏圆的内外分点，且：

阿氏圆原理给二维平面上无人机追逃问题提供了思路：若E、P分别为二维平面上逃跑无人机和追捕无人机所在的初始位置，则当逃跑无人机和追捕无人机都按照理想的匀速直线运动，且逃跑无人机的速度vE和追捕无人机的速度vP的比例为vP/vE=k时，逃跑无人机刚好可以在阿氏圆上被追捕无人机截获。

图2为将阿氏圆应用于无人机的追逃模型。

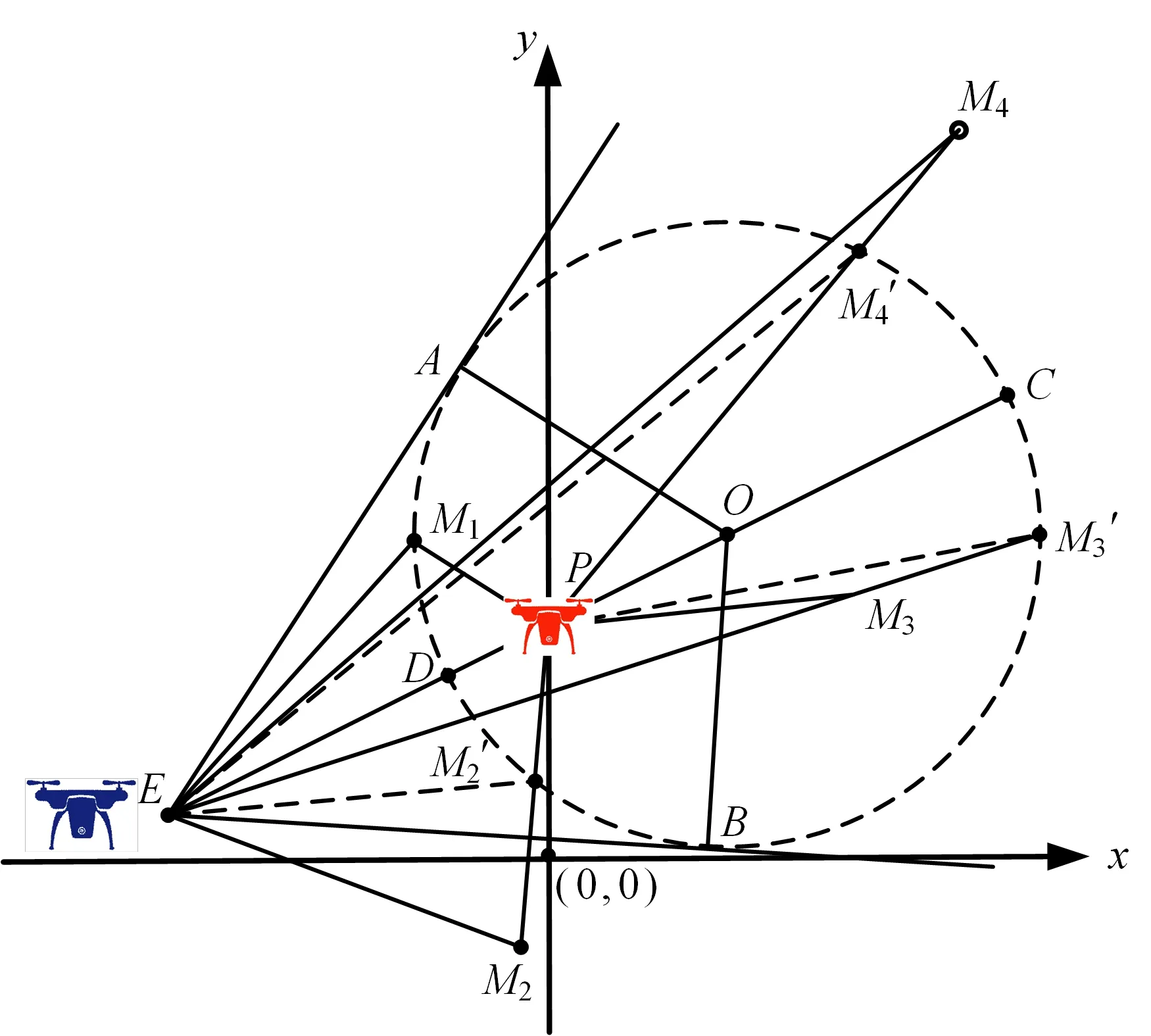
图2 2个单无人机追逃模型

图2中E、P分别代表逃跑无人机位置和追捕无人机位置，其坐标分别为：E(xE,yE)和P(xP,yP)，则可以得到阿氏圆的坐标为：

阿氏圆的半径为：

假定逃跑无人机和追捕无人机均以恒定速度直线运动，逃跑无人机的速度和追捕无人机的速度分别为vE和vP，vP/vE=k＜1，E A和E B分别为点E对阿氏圆的切线，A、B分别为切点，则上述追捕问题可以概括为以下3种情况：

1）捕获点在阿氏圆上

即追捕无人机刚好在阿氏圆上点M1截获到逃跑无人机。

2）无法捕获

因此，逃跑无人机比追捕无人机先到达M2，追捕无人机无法截获逃跑无人机。

3）捕获点在阿氏圆内

追捕无人机在阿氏圆内就可以成功截获逃跑无人机。

上述2个单无人机追逃模型的构建对问题进行了简化，即假设逃跑无人机和截获无人机都按照匀速直线运动进行逃跑和截获，没有运动速度和方向的改变，这种简化可以求解一个极端情况，即在追捕无人机已经知道逃跑无人机的逃跑意图和路线，但是在绝对实力面前，逃跑无人机是否一定能够在一定范围内逃逸成功的问题。这种情况对于指导逃跑无人机的逃跑方案规划是有用的，可以在逃跑无人机速度大于追捕无人机的情况下求得逃跑无人机的绝对逃逸区域。

2 多无人机追捕模型构建

对于多个追捕无人机追捕模型，只需要将第1节中单追捕无人机模型进行扩展即可。按照第1节给出的单无人机模型中阿氏圆的构建，构建多个追捕无人机相对于逃跑无人机的阿氏圆。图3为含有n个追捕无人机和单个逃跑无人机的追逃示意图。

图3 多个追捕无人机追捕模型

设逃跑无人机的起始位置为E(x E,y E)，追捕无人机的起始位置分别为：P1(x1,y1)，P2(x2,y2)，…，P n-1(x n-1,y n-1)，P n(x n,y n)，追捕无人机和逃跑无人机依然采用合适策略按照匀速直线运动，且追捕无人机和逃跑无人机的速度比为：

则第i个追捕无人机P i相对于逃跑无人机的阿氏圆O1,O2,…,O n，如图3所示，第i个阿氏圆的圆心坐标可以求得为：

第i个阿氏圆的半径可以求得为：

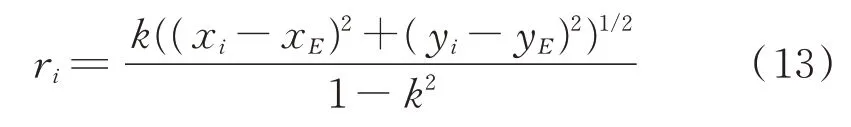
相邻2个阿氏圆O m和O m+1的圆心距可以计算为：

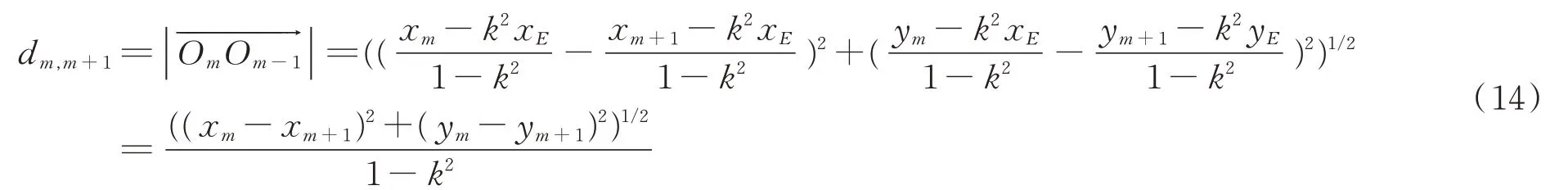
当d m,m+1＞r m+r m+1时，相邻2个阿氏圆不相交，即逃跑无人机只要采取相应策略，一定可以从第m个追捕无人机和第m+1个追捕无人机之间逃逸。

由式（13）和（14）可以进一步将逃跑无人机从第m个追捕无人机和第m+1个追捕无人机之间进行逃逸的条件化简为：

反之，逃跑无人机不能从第m个追捕无人机和第m+1个追捕无人机之间进行逃逸的条件为：

因此，逃跑无人机一定能够成功逃逸的条件为存在阿氏圆O m′和O m′+1，使得d m′,m′+1＞r m′+r m′+1；反之，只要追捕无人机采取合适追捕策略，就一定能够成功追捕到逃跑无人机的条件为对于任意阿氏圆O m″和O m″+1，d m″,m″+1≤r m″+r m″+1。

由式（15）、（16）和（11）可以看出逃跑无人机能否逃逸的条件只取决于逃跑无人机和追捕无人机的起始位置与速度，因此逃跑无人机在逃逸时只需要知道追捕无人机的速度和起始位置，就可以知道在最坏条件下，即追捕无人机采取最优追捕策略时，自己能否逃逸。

3 仿真及分析

本节考虑单个逃跑无人机和2个追捕无人机在二维平面的追逃情况，如图4所示。假设存在由边A D和B C构成的平面通道，通道宽度为M，逃跑无人机可以处于通道的任何位置，2个追捕无人机分别位于G1和G2，现逃跑无人机需要从通道左边向右逃逸，实验旨在求得逃跑无人机的绝对逃逸区域，即不论追捕无人机采取什么样的追捕策略，逃跑无人机一定能够逃跑的绝对逃逸区域。

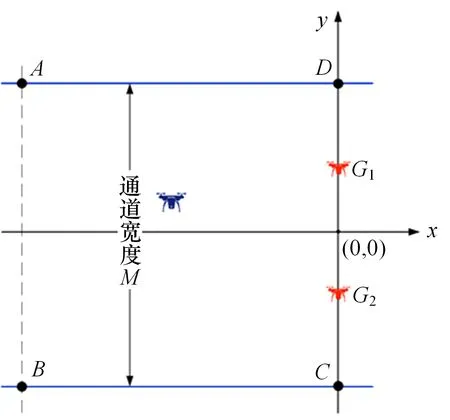
图4 单个逃跑无人机和2个追捕无人机在二维平面的追逃示意图

实验设置通道宽度M=70 km，D G1=C G2=20 km，逃跑无人机的速度为v E=250 m/s，追捕无人机的速度为v P=200 m/s，以第2节中逃跑无人机的逃跑条件为判断准则，通过仿真实验，得出逃跑无人机的绝对逃逸区域如图5所示。

图5中深色区域为逃跑无人机的绝对逃逸区域，即当逃跑无人机位于深色区域时，不论捕获无人机采取什么样的截获策略，逃跑无人机一定能够成功逃逸，原因在于当逃跑无人机在此区域时，阿氏圆总是不相交的，也就给逃跑无人机提供了逃跑空间。

此外，根据逃跑无人机选用的逃跑路线可以将图5中的绝对逃逸区划分为5部分：上侧逃逸区、中间逃逸区、下侧逃逸区、双侧逃逸区1和双侧逃逸区2，如图6所示。当逃跑无人机位于上侧逃逸区时，逃跑无人机只能选择从G1上侧逃逸；当逃跑无人机位于中间逃逸区时，逃跑无人机只能选择从G1与G2之间进行逃逸；当逃跑无人机位于下侧逃逸区时，逃跑无人机只能选择从G2下侧段进行逃逸；当逃跑无人机位于双侧逃逸区1时，逃跑无人机可以选择从G1上侧或G1下侧进行逃逸；当逃跑无人机位于双侧逃逸区2时，逃跑无人机可以选择从G2上侧或G2下侧进行逃逸。

图5 逃跑无人机的绝对逃逸区域

图6 绝对逃逸区域划分示意图

还可以观察到绝对逃逸区域关于x轴对称，这是由于选择的初始化参数D G1与C G2相等，因此G1与G2关于x轴对称所导致。

此实验为平面区域内对于单一逃跑者和2个追逃者条件下的追逃实验，在一定条件约束下，求得了逃跑无人机的绝对逃逸区域，即只要当逃跑无人机初始位置在绝对逃逸区域内时，即使追捕无人机完全清楚逃跑无人机的意图，采取最优策略，逃跑无人机也一定能够逃跑。在实际中追捕无人机不一定有条件采取最优策略，这为逃跑无人机的逃逸进一步提供了空间，逃跑无人机的成功逃逸区域则会更大。

4 结束语

本文基于阿波罗尼奥斯圆原理构建了2个单无人机追逃模型和多无人机追捕模型，给出了逃跑无人机和追捕无人机能够成功逃逸及成功追捕的条件，当追捕者和逃跑者构成的阿氏圆存在间隙时，逃跑无人机能够成功逃逸；反之，当阿氏圆不存在间隙时，追捕者采取合适的策略，一定能够成功截获逃跑者。此外，本文还对模型进行了仿真分析，仿真结果表明在二维平面的逃逸通道内，存在一个绝对逃逸区域，只要逃跑无人机初始位置位于此区域，逃跑无人机就一定能够成功逃逸。