基于频谱不对称性的雷达辐射源个体识别*

刘鲁涛，安赛龙

（1.哈尔滨工程大学信息与通信工程学院，黑龙江 哈尔滨150001；2.哈尔滨工程大学先进船舶通信与信息技术工业和信息化部重点实验室，黑龙江哈尔滨150001）

0 引言

随着电子信息技术的迅猛发展，电子战技术的广泛使用已经成为现代战争的主流，敌对双方在电子战中的综合实力将会影响战争的走势。辐射源个体识别是电子支援措施和电子情报系统最困难的任务之一，试图通过分析截获的雷达信号来识别单个雷达辐射源，从而确定敌方雷达的位置、性能和技术水平等相关信息。因此，在复杂多变的电磁环境下精准识别敌方的雷达辐射源具有重要的军事意义[1]。

传统的辐射源个体识别方法主要通过提取雷达信号的脉冲描述字参数特征来实现，如到达时间、到达方向、脉冲宽度、脉冲重复间隔等。随着电子信息技术的发展，基于脉冲描述字的参数特征已无法满足雷达辐射源个体识别的需求，为了识别复杂电磁环境下的雷达辐射源，需要分析每个脉冲的内部结构，称为脉冲的无意调制。脉内无意调制是由于雷达辐射源内部的电子元器件的细微差别而造成的寄生调制，这种无意调制普遍存在并且很难彻底消除[2]。

目前，根据特征的性质，把提取的特征主要分为时域特征、频域特征和变换域特征[3]。时域特征包括瞬时幅度、瞬时相位、瞬时频率[4]等，频域特征包括双谱[5]、短时傅里叶变换[6]等，变换域特征包括模糊函数[7]、变 分 模 态分解[8-9]、小波包变换[10]、分形方法等[11]。时域特征容易受到噪声的影响，变换域特征需要进行复杂的变换，本文利用频谱的不对称性来进行个体识别，提出基于频谱不对称性的辐射源个体识别算法，并利用实测信号对该算法进行了仿真验证。

1 信号无意调制建模

线性调频信号(LFM)是一种常见的雷达调制信号，信号表达式如下：

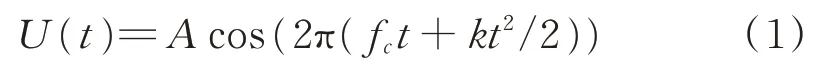
式中，f c是载波频率，k=B T是调频斜率，B是频率变化范围，T是一个脉冲的宽度。

无意调制会引起频率漂移、脉冲包络的改变和相位噪声[12]。其中，脉冲包络的改变和频率漂移对信号的影响较小，相位噪声对信号的影响是最大的，对于理想的LFM信号，加入相位噪声后形式变为：

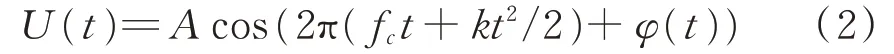
式中,φ(t)为相位上的无意调制，定义无意调制相位噪声模型为：φ(t)=αsin2πf m t，则LFM信号表达式U(t)可以改写为：

相位噪声是由无限个随机信号调制的综合结果，所以最终可表示为：

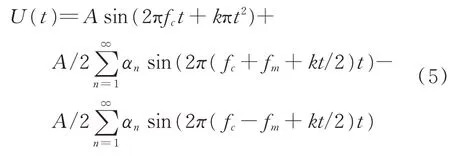
从无意调制模型中可以看出相位噪声将在f c±f m+1 2k t处随机产生多个边带，并且会在中心频率两侧产生不同的边带，这将会造成频谱的不对称。因无意调制具有唯一性，即每个辐射源的无意调制特征都是独一无二的[13]，所以提取频谱的不对称性水平就可以实现辐射源的个体识别。

2 频谱不对称性评估

2.1 分数阶傅里叶变换估计LFM参数

中心频率的精确定位是评估频谱不对称性的关键，鉴于分数阶傅里叶变换(FRFT)非常适合处理Chirp这种非平稳信号，故采用FRFT方法来估计LFM信号的参数。

定义在时间域上的线性调频信号U(t)，其p阶FRFT表示为：

式中，K p(t,u)=Aαexp(jπ(u2cotα-2utcscα+t2cotα))是FRFT的核函数，FRFT的阶数为p，旋转角度为α=pπ/2。

随着旋转角度的不同，信号在分数阶域的能量聚集性也会随之改变。只有在最优旋转分量时，信号在分数阶域的能量聚集性是最强的[14]，此时，FRFT的结果为冲激函数δ(f0-ucscα)。图1为在不同的旋转角度时分数阶域的结果示意。

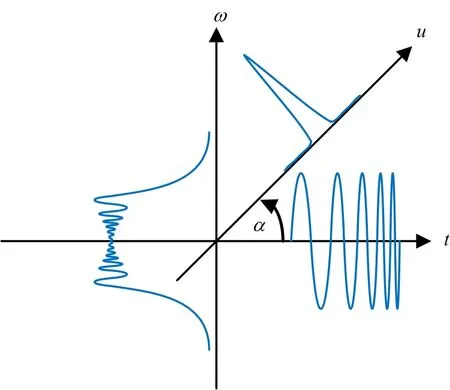
图1 分数阶变换角度旋转示意

对LFM信号做FRFT，把阶数p当做检测所用变量，以Δp为搜索步长，在p∈[0,2]范围内计算不同阶次下的FRFT，得到信号在(p,u)平面中的能量分布，在整个时频域中进行二维搜索，找到能量峰值点所对应的(p0,u0)。利用最佳阶次计算出最佳旋转角度α0=p0π/2，然后就可以对LFM信号的调频斜率μ0和中心频率f0参数进行估计[15]。

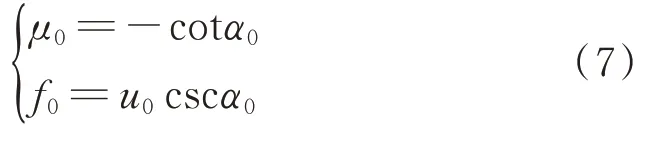
根据调频斜率、采样点数N和采样频率f s估计出带宽B0。

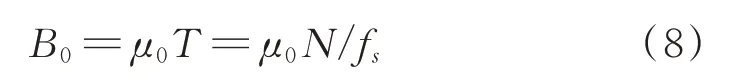
2.2 改进的FRFT算法

当需要较高的参数估计精度时，需要减小步长Δp，但同时也会使计算量成倍增加。当搜索步长Δp=0.000 01时，可以满足精度要求，但需要计算200 001次，计算量很大。为了减小计算量，采用多次粗估计来确定最佳阶次所在区间，最后采用一次精估计来确定最佳阶次。

根据文献[14]可知，信号分数阶频谱4阶原点矩更适合低信噪比下最优阶次的快速估计，因此利用分数阶频谱的4阶原点矩来估计最佳阶次。首先令步长Δp=0.1，在p∈[0,2]的区间内计算分数阶频谱的4阶原点矩，选出当4阶原点矩最大时对应的阶次p0，然后更改区间令p∈[p0-Δp,p0+Δp]。确定区间后重新进行一次粗估计，更改步长令Δp=0.1Δp，计算出此时4阶原点矩最大时对应的阶次，更新最优阶次p0。当进行4次粗估计后更新区间p，更改步长为Δp=0.000 01，在新的区间内进行精估计，此时求得的最优阶次p0就可以用来估计LFM的参数。改进后的FRFT只需要计算105次，大大减小了计算量，改进算法流程图如图2所示。

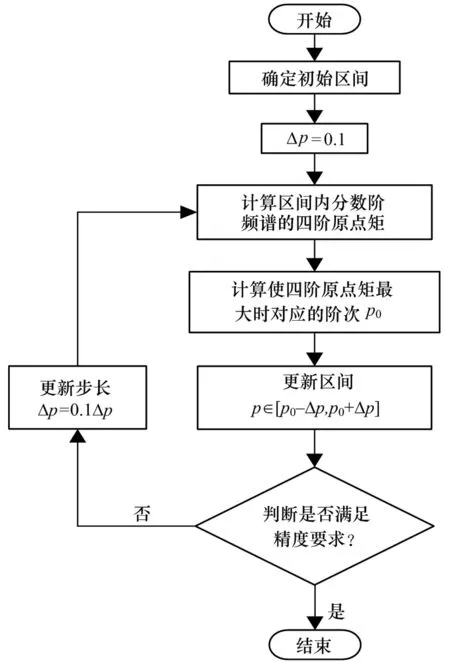
图2 改进算法流程图

2.3 频谱不对称性评估

要估计频谱的不对称性，需要把时域信号x(t)转换到频域X[k]。首先把时域信号进行预处理，去除时域信号的均值，然后进行归一化处理。为了避免原始信号中突变点或野值点带来的影响，本文通过取脉冲包络顶部的多个点，计算得到平均幅值，并除以平均幅值进行归一化。

运用改进后的FRFT算法对归一化后的时域信号进行参数估计，估计出LFM信号的中心频率f0和带宽B0。然后采用N点快速傅里叶变换算法(FFT)计算出时域信号的频谱X[k],k=1,2,…,N-1，并将频谱归一化。

公式(9)中的f l i p{·}表示向量的翻转，τ是对中心频率校准，在-2≤τ≤2的情况下使X l和X r的欧式距离最小。

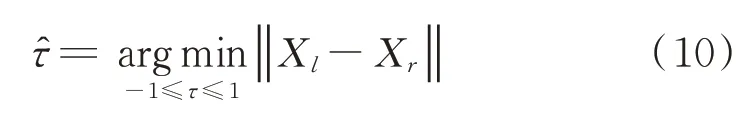
把̂代入到公式(10)中计算出校准后的X l和X r。

在计算出左右频谱后，通过能量差、欧几里得距离和相关系数来评估频谱的不对称性。因相位噪声的影响，在左右频谱中随机产生的多个边带是不同的，这将会造成左右频谱的能量存在差别，故可以以左右频谱的能量差作为特征进行识别。

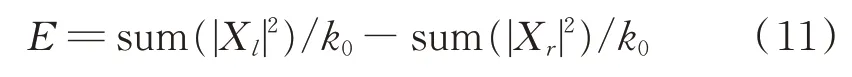
欧几里得距离，又称欧式距离，是一种用来度量相似度的算法，欧式距离越小，相似度就越大，欧式距离越大，相似度就越小。

相关系数也可以用来衡量X l和X r的相似度，定义为：

公式(13)中Cov(·)表示计算协方差，Var(·)计算方差。ρ的取值范围为[-1,1]，相关系数|ρ|越接近0，表示相关性越小，|ρ|越接近1，表示相关性越大。

把计算得到的能量差、欧式距离和相关系数特征组成联合特征向量来进行雷达辐射源的个体识别。

3 支持向量机(SVM)分类器

支持向量机是在统计学习理论的基础上并根据结构风险最小化的原则提出的一种新的机器学习方法[16]。根据决策平面原理，找到一个用来分割不同类型数据的决策平面，各类数据到此决策平面的距离之和越大，分类的可信度也就越大，因此，支持向量机的关键问题是找到距离各类数据距离之和最大的决策平面，此决策平面为最优分类超平面。

假设有l个训练样本(x1,y1)，(x2,y2),…，(x l,y l)，其中x i∈R n，y i∈{+1,-1}，用于分类的超平面为(ω⋅x)+b=0。当H1与H2平面距离d=2/‖ ‖ω最大时，超平面才是最优的，因此，SVM的关键问题由找到最优分类超平面转变为解决相应的优化问题。

当训练样本满足线性可分条件时：

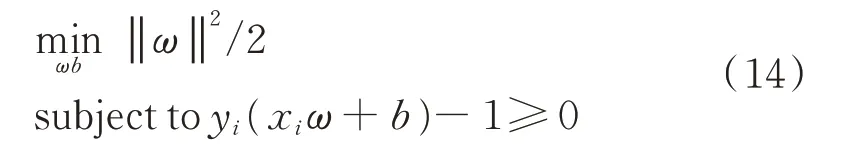
引入拉格朗日乘子αi,αi≥0，构造拉格朗日函数L。

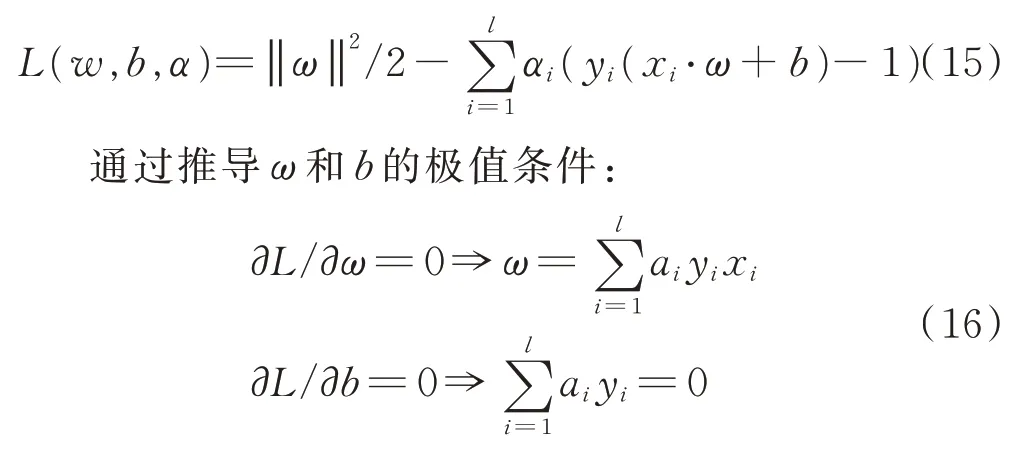
求解得到的不为零的αi所对应的样本点就构成了H1、H2平面，根据H1、H2就可以求出超平面，其对应的决策函数为：

当样本不满足线性可分条件时，就需要把样本空间向高维空间进行映射，新空间的样本能够满足线性可分的条件。这时为了求出决策函数就需要引用一个松弛变量ςi,ςi＞0，公式变为：

推导出决策函数表达式为：

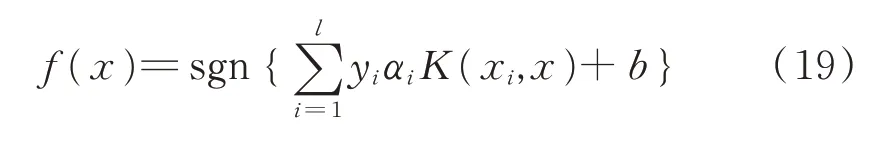
式中，核函数为K(x i,x)=φ(x i)φ(x)，φ(x)为x i映射后的样本。

SVM只能实现二分类，要想实现多分类，需要训练多个二分类器。当分类个数为m时，对m类样本中每2类训练一个分类器，共需要m(m-1)/2个二分类器。对于一个未知样本，需要经过所有的二分类器进行预测，最后通过投票决定样本的最终类别。

4 实验与分析

4.1 数据采集

本文所用数据皆为实测数据，采用Tektronix AWG70001任意波形发生器、Keysight E4438C ESG矢量信号发生器、2部Keysight N5172B X系列射频矢量信号发生器和Keysight N5182B X系列射频矢量信号发生器共5部辐射源来生成LFM信号。用实测信号来模拟真实的雷达信号，把5部辐射源分别命名为radar1、radar2、radar3、radar4、radar5。采集时设置带宽为20 MHz，中心频率为1 GHz，采样频率为25 GHz。每部辐射源采集120个脉冲信号，取其中80%的数据用于训练，剩下的20%用来测试。

4.2 频率估计误差

利用FRFT算法进行了100次蒙特卡洛实验来估计中心频率，并计算估计出的频率与采集信号时设定的频率之间的误差，如表1所示。

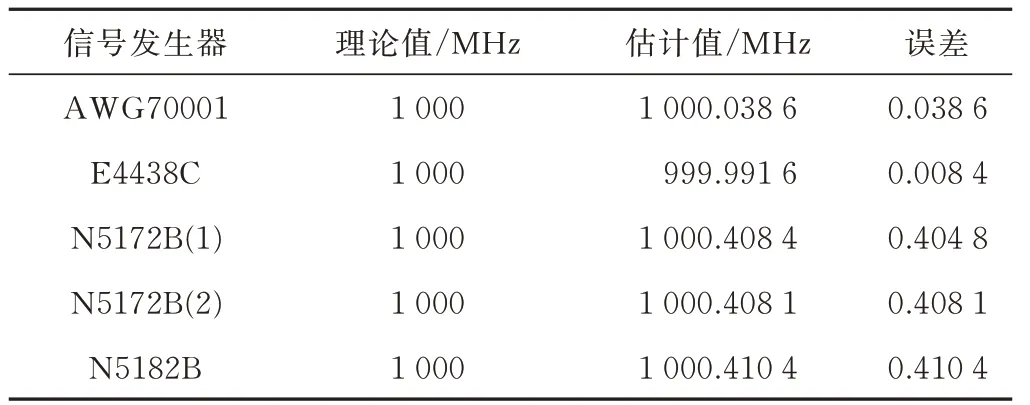
表1 中心频率的估计结果

从表1中可以看出，采用FRFT方法来评估中心频率误差较小，可以用来作为中心点来划分左右频谱。

图3是把估计的中心频率作为特征进行识别的识别结果混淆矩阵，从图中可以看出，识别率只有73%。表明5部信号发生器产生的信号中存在频率漂移现象，但漂移量很小，仅仅以估计的中心频率作为特征区分不出这5部辐射源。

图3 识别率混淆矩阵

4.3 频谱不对称性仿真结果

在估计出中心频率后，以估计出的中心频率为中心，把信号的频谱分为左频谱和右频谱2部分。

图4—8展示了5部雷达辐射源个体左右频谱的不对称性。从图中可以看出，频谱的左右频谱的对称性已经被相位噪声破坏，并且对不同辐射源的破坏程度是不同的。

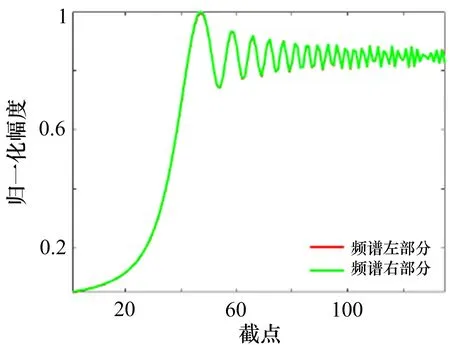
图4 radar1的频谱不对称性

图5 radar2的频谱不对称性

图9为5部雷达辐射源三个特征的聚类结果，可以看出，5部雷达辐射源的特征在小范围内聚集，不存在特征交叠现象，说明这三个特征比较稳定，可以利用这三个特征来进行个体识别。

图6 radar3的频谱不对称性

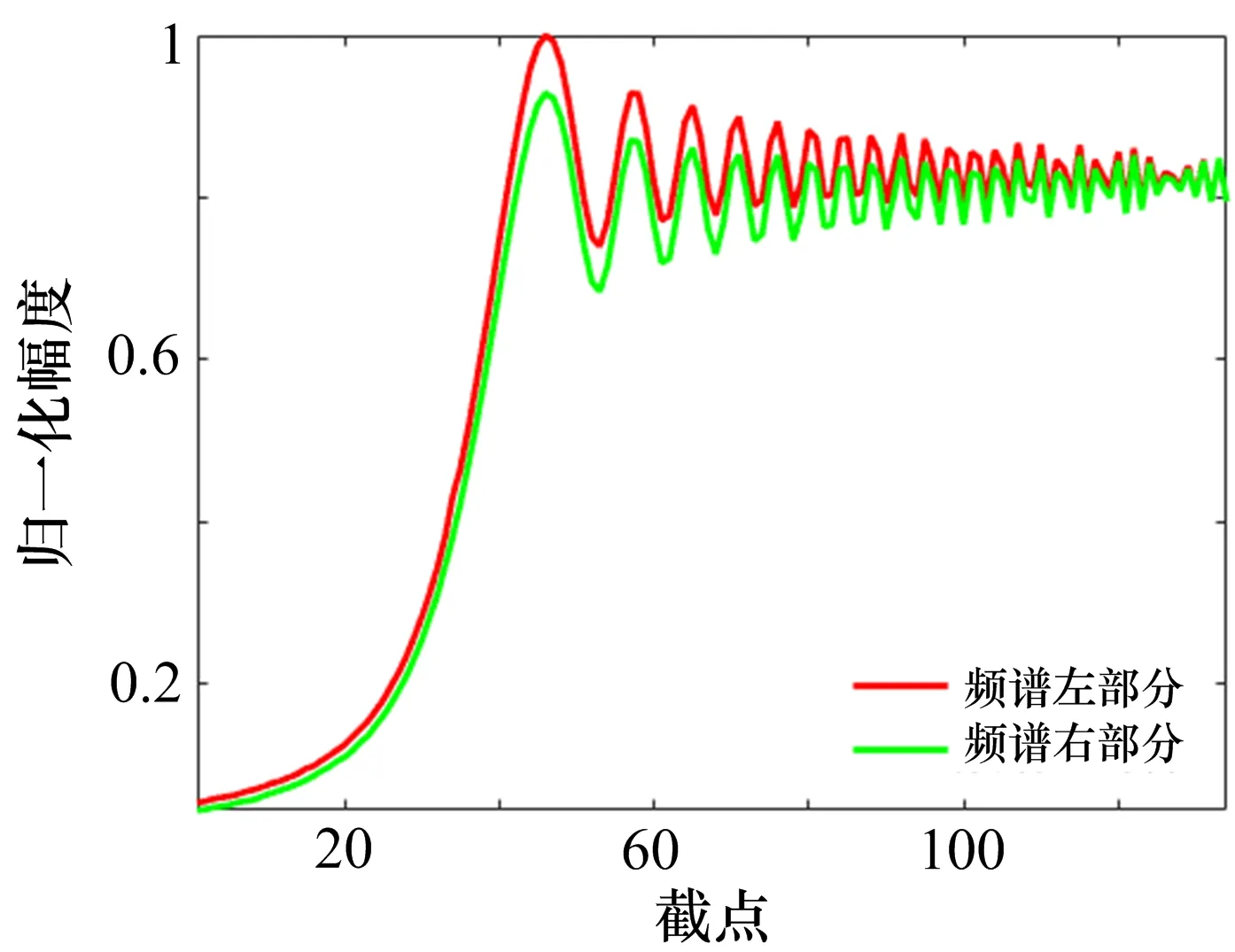
图7 radar4的频谱不对称性

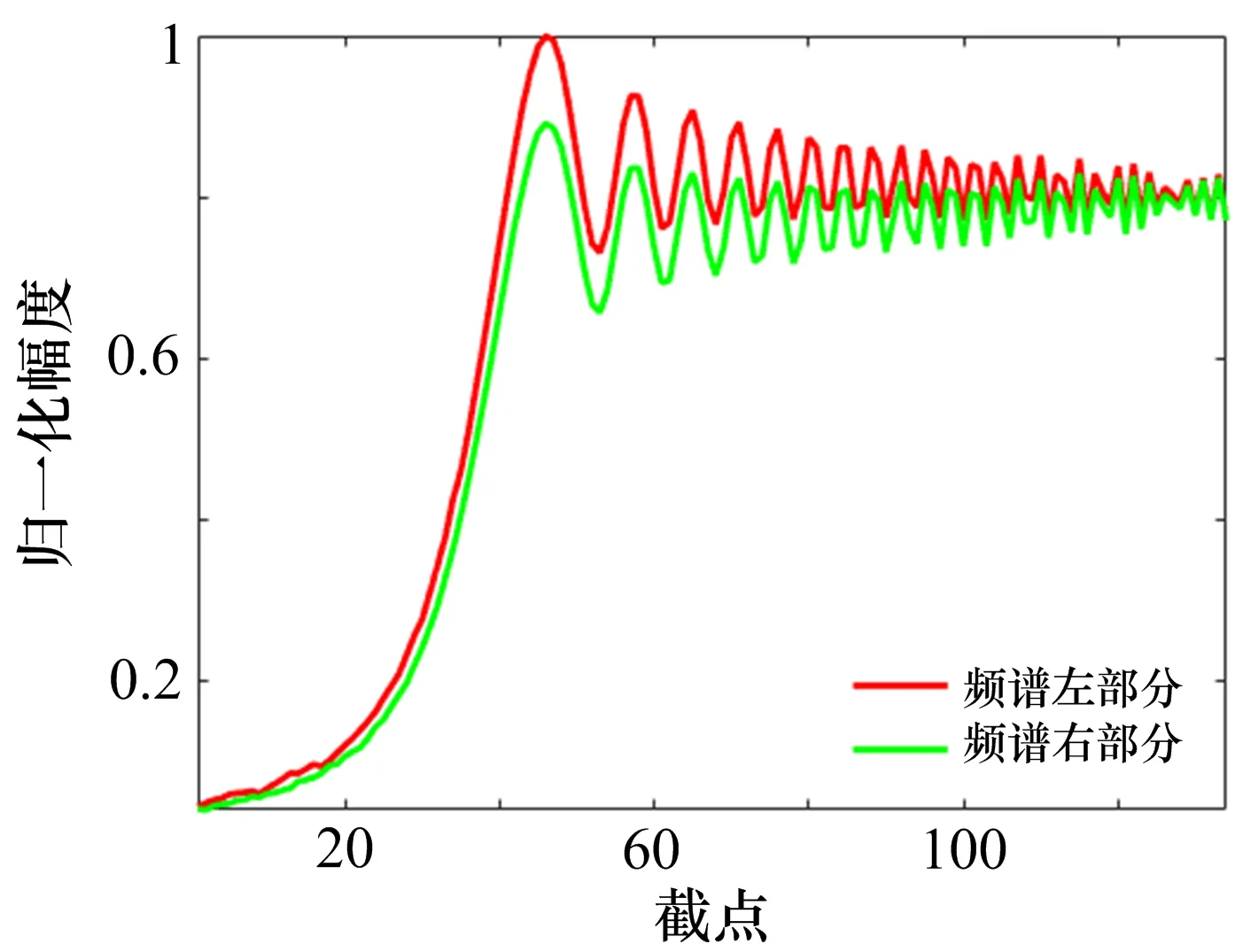
图8 radar5的频谱不对称性

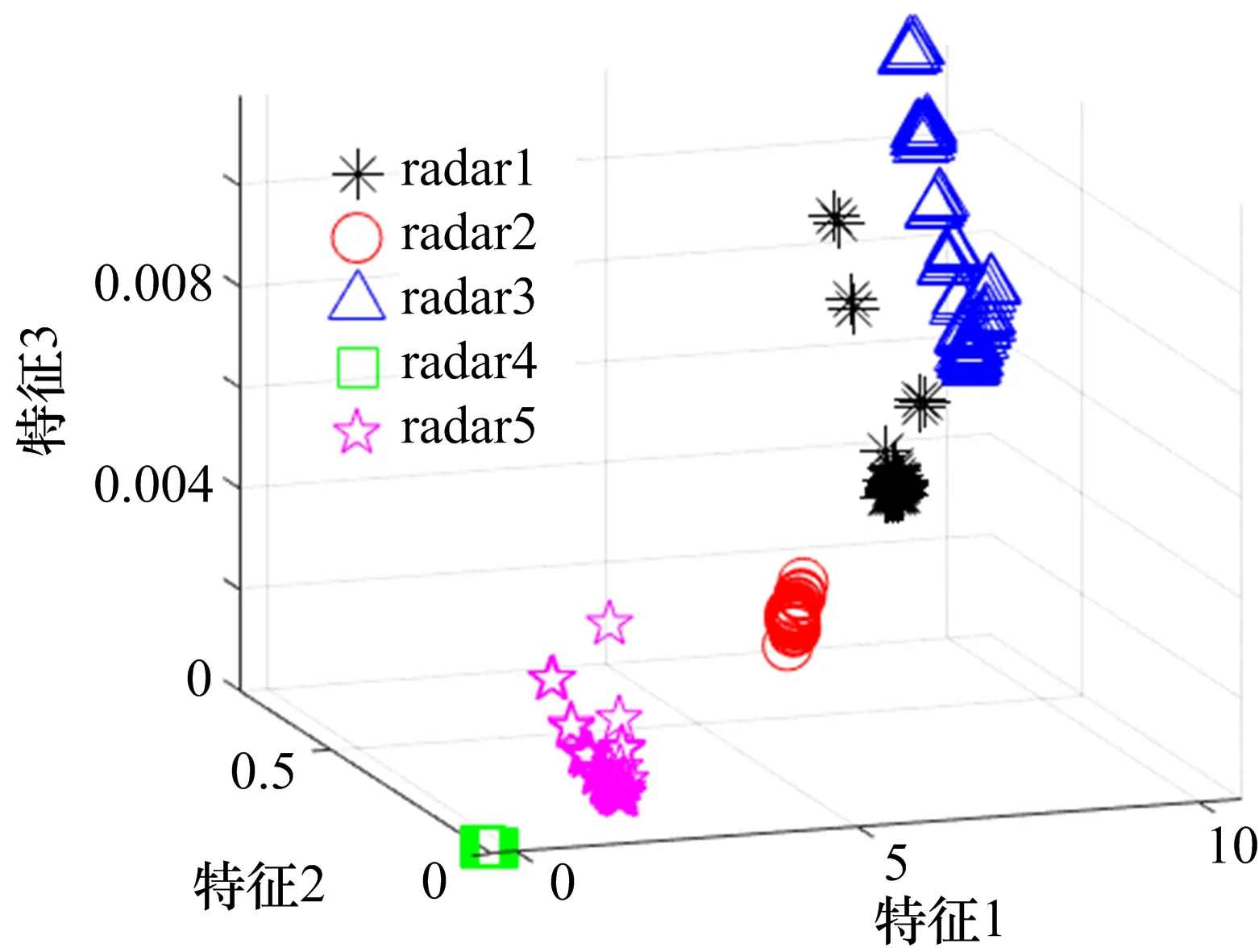
图9 三个特征的聚类结果

给采集到的信号添加高斯白噪声，并计算在不同的信噪比下，通过评估不对称性进行个体识别的识别率。并与文献[9]中提取VMD分解后奇异值作为特征的方法和文献[10]中提取小波包能量作为特征的方法进行比较，仿真结果如图10所示。

图10 识别结果对比

从识别结果对比中可以看出，在信噪比为-5～20 d B的条件下，利用频谱不对称特征来进行个体识别方法的正确识别率高于文献[9]和[10]中所提方法，尤其是在低信噪比情况下。本文所提方法在信噪比高于5 d B时，识别率可达到100%，即使信噪比在-5 d B时，正确识别率仍可达到90%，证明了基于频谱不对称性的方法对雷达辐射源个体有着很好的识别效果。

5 结束语

本文主要研究雷达辐射源个体特征提取与识别，首先分析了无意特征产生的机理，并针对信号的无意调制进行建模，发现无意调制会造成频谱的不对称，可以利用该特性来进行辐射源的个体识别。然后用FRFT算法来估计中心频率，提取出左右频谱，以左右频谱的能量差、欧式距离和相关距离为特征，送入到SVM中进行识别。将仿真结果与其他特征提取方法对比，结果表明，本文所提方法在不同信噪比下都具有较好的识别效果。本文主要研究了LFM信号，对于其他脉内调制方式的信号还需要进一步研究。