资源约束条件下任务调度算法研究
2021-11-29路程昭龚建兴
路程昭, 龚建兴, 朱 雷, 刘 权
(国防科技大学智能科学学院, 湖南 长沙 410073)
0 引 言
资源约束条件下的任务调度问题(resource-constrained task scheduling problem, RCTSP)是一个涉及众多领域的关键问题,比如并行计算、软件开发和工程建造等。特别在应急管理领域(如地震救援和突发公共卫生事件),该问题是影响应急处置效果的核心问题。RCTSP通常存在任务之间关系复杂、资源紧缺或补充不及时的特点,被证明是NP完全问题[1],复杂度高,实现高效任务调度和资源分配难度大。
针对RCTSP,国内外学者已经进行了大量的研究,涉及云计算[2-5]、分布式系统[6-7]、流水线生产[8]等多个领域。研究内容还包括问题的分析、建模、求解、应用等多个方向,例如,Orr[9]基于分配排序模型,提出了一种状态空间模型,用于解决存在重复任务的最优调度问题,任务重复调度可以缩短时间表总长度,并且可以给出最佳的任务重复计划;Krishnakumar[10]提出了一种基于模仿学习的方法,用于在处理无线通讯和雷达系统应用程序的多核心平台进行任务调度,通过提供一个分层学习框架,从已开发的任务调度策略学习,最大程度减少应用程序执行时间;田启华[11]采用多目标理想法构造评价函数,选择最优任务调度方法;Wang[12]建立了一种新型的分布式成像卫星紧急任务多目标动态调度模型,提出了一种综合考虑任务合并、后移、复原的动态调度算法;Yuan[13]根据早期树对所有任务进行分组,对于关键活动和非关键活动采用不同的优化算法;Lin[14]针对多技能资源受限项目调度问题提出一种遗传规划超启发算法,将遗传程序作为管理低级启发式的高级策略;Kosztyanzt[15]研究了灵活项目管理的调度方法,提出了一种基于矩阵的方法,包含灵活任务依赖性和未定补充任务完成情况,处理新的未调度任务,讨论了传统的多模式资源受限项目调度问题;Ali[16]提出了一种过滤矩阵方法,将大规模工作流划分为子工作流以提高调度的效率。
关键路径技术同样在任务调度相关领域得到广泛应用,Abrishami[17]提出了基于部分关键路径的工作流调度算法,递归计算以当前节点为结束的关键路径;张艳[18]提出了一种新的基于关键路径的递归调度算法,对调度节点进行递归选择,结合它的后继任务确定最佳时间槽;Takakura[19]对经典的关键路径方法进行改进,在目标完成时间内使过程完成概率最大化,并利用生产系统中的历史数据来处理不确定的任务工期;柳玉[20]分析最长关键路径算法,提出一种运用结点信息流量减少CPU空闲时间碎片的并行任务调度优化算法;Wang[21]针对多模式资源受限的项目调度问题提出了7个离散时间模型,扩展了关键路径方法,以解决替代性先决条件活动的情况;Ramezani[22]提出了一种基于启发式的动态关键路径感知调度技术,用于在多现场可编程门阵列系统上调度任务;Maurya[4]使用有效关键路径,提出一种基于聚类的调度算法,用于最小化给定应用程序的调度长度。上述文献均在关键路径技术的基础上运用各自提出的方法解决实际问题。
在现有文献中[15,23-24],RCTSP又被称之为资源约束条件下项目调度问题(resource-constrained project scheduling problem, RCPSP)。总体来看,该问题已经有了大量的研究。但是目前已有的算法在考虑资源约束时,通常将单个任务所需的资源考虑为固定量,没有考虑在资源不足时执行任务产生的效果和影响;RCTSP的研究多是从避免资源冲突角度出发,对已产生资源冲突的消解研究相对较少;另外目前鲜有在地震救援情景问题上采用任务调度算法并验证有效性的研究。
针对现有问题,本论文的工作如下。
(1) 本文基于工作流图模型,完成了对资源约束条件下任务调度的建模,提出了任务调度与资源冲突消解的框架。
(2) 本文提出了两种任务调度算法,实现对调度过程中资源冲突的消解:一种是通过任务关键度确定优先级,并基于贪心策略和调整工作流图拓扑结构方法的算法;另一种是采用弹性资源调度的方法,为产生资源冲突的任务分配现有不充足资源的任务调度算法(task scheduling algorithm based on elastic resources, ER)。
(3) 本文通过一个地震救援的案例背景,验证了本文提出的资源约束条件下任务调度算法的可行性,并通过随机生成的算例,将本文提出的算法与两类RCPSP典型求解方法中的代表性算法进行对比。
1 问题描述
RCPSP主要面对复杂的情景下,存在先后逻辑顺序、可能产生资源冲突的一系列任务的调度。任务调度主要涉及任务优先级确定、开始时刻安排、资源分配等问题,由于问题本身的复杂性或时间紧迫性,其求解存在一定的困难,因此需要建立模型对此类问题进行描述,设计符合相应需求的算法。
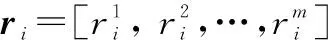
定义 1前驱任务和后继任务。对于
∀vi,vj∈V,∃eij>0
(1)

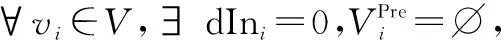
定义 3截止时间。整个项目所有任务执行完毕所需要时间定义为截止时间,记作T。
(2)
(3)
DAG中每个节点包含任务所需资源、任务所需时间、最早开始时间、最晚开始时间4个参数,工作流图的表示如图1所示。
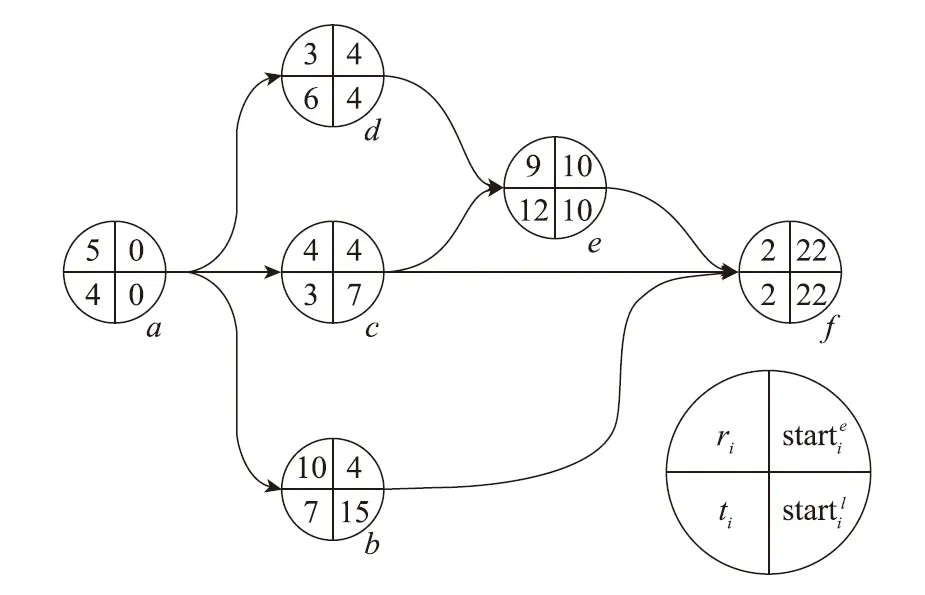
图1 包含4个参数的工作流程图Fig.1 Workflow diagram with four parameters
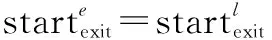
(4)
2 模型构建
2.1 关键任务的确定
定义 6关键任务。定义工作流中,对项目整体完成存在显著影响效果的任务为关键任务。例如,在地震救援过程中,关键任务通常指对救援进程起决定性作用的任务:交通要道抢修、现场指挥部建立等救援过程中的核心任务。
在不考虑资源约束的工作流图中,关键路径上的任务执行时间决定了整个项目的截止时间,因此常把关键路径上的任务作为关键任务。而在考虑资源约束的条件下,可能存在非关键路径上的任务对整个项目完成的影响更大的情况。文献[11]提出用任务执行的成功率作为关键任务的确定方法;文献[18]采用递归计算动态关键路径;文献[25]采用预先设定的优先级判断任务的关键程度。可以看出,关键任务的确定不仅是一个定性分析的过程,而且需要定量分析的手段,本文提出关键度的概念来描述任务的关键程度。
定义 7关键度。任务的关键度定义为:设任务执行时间增加1,项目截止时间增加的量,记作δi,计算如下:
(5)
资源约束下的任务调度问题存在一定复杂性,若计算n个任务中每个任务的关键度,则时间复杂度为O(n2),计算量随着任务数的增加快速增长,无法适应例如地震情景下的复杂性、决策快速性要求。因此,选择使用每个任务相关参数来估计任务的关键度,算法的时间复杂度降为O(n)。
本文通过构建评估函数来估计工作流中任意任务的关键性,评估函数E(vi)表示如下:
(6)
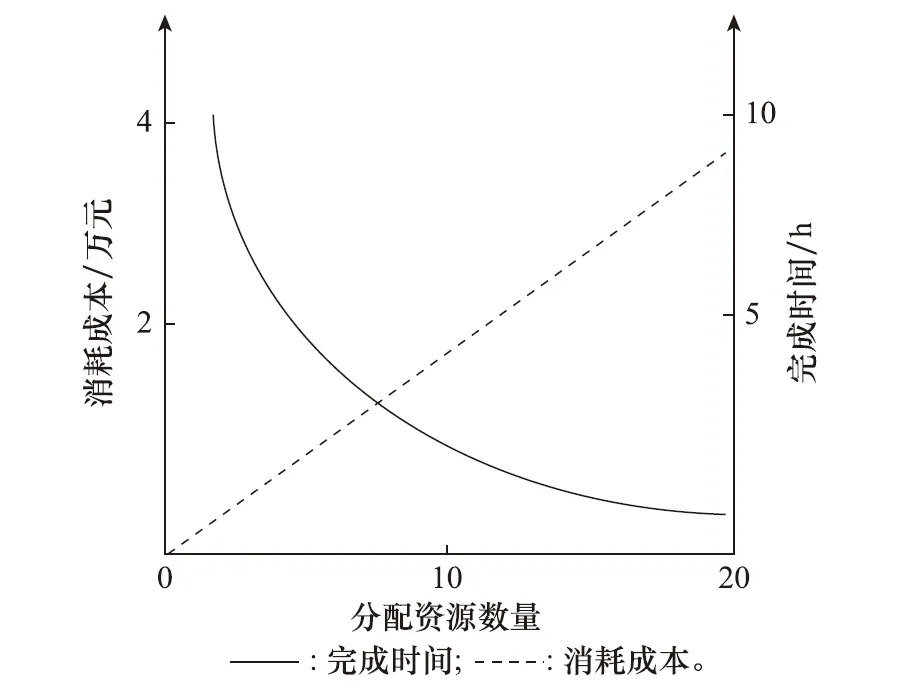
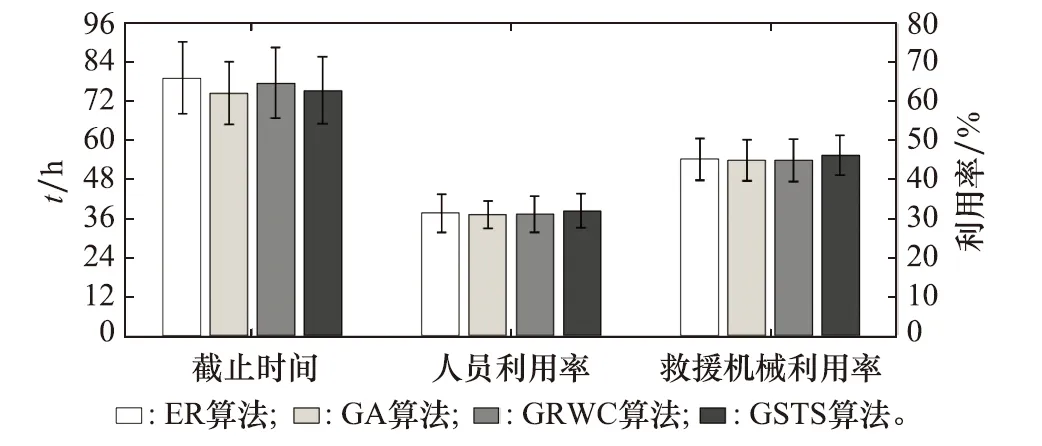
上述评估函数,综合考虑了可能对任务关键性产生影响的量,其中η、λ、μ、σj为每个量对应的权重系数。权重系数可以通过经验估计来计算,理想情况下,使得对于所有δa<δb都存在E(va) 由于RCTSP中任务存在关联和前后逻辑关系,并且同一时间内的资源数量有限,多项任务同时开展可能产生资源冲突,需要进行冲突的消解。任务调度可以看作是为各个任务在合适的时间,分配一定量资源的过程。通过调度实现目标函数的最优化,并且保证满足约束条件,可以用线性规划方程[19]来表示: (7) (8) 式中:pi和αi分别表示任务i所需要的成本和相应的加权系数,式(8)第1行表示关键路径上任务执行时间和,小于截止时间Td;第2行表示在任意时刻τ的m种资源剩余数量不为负;bk表示任务k的开始时刻,cl表示任务l的完成时刻;第3行表示任务的完成时刻,大于其所有前驱任务最大完成时刻,限制每个任务在其前驱任务完成后才能开始;第4行限制任意任务i开始时刻不小于0时刻,且救援任务截止时间大于0。 通常在任务调度问题中,任务需求资源数量等于系统分配给任务的数量。而在一些实际问题中,资源不充足条件下,任务依然能够开始。例如,地震灾害发生的初期,地震救援所需要的资源很难完全得到满足,考虑到救援活动的紧迫性,通常选择将现有资源先全部投入使用,等待后续救援。利用这种思想,本文提出为任务弹性分配资源的方法。 (9) f(ri)可以分为两部分,一部分为每种资源量变化独立对任务执行时间产生影响;另一部分为几种资源变化共同作用对任务执行时间产生影响。上述函数的具体形式通常与任务和资源的具体性质相关。例如:地震救援中搬运作业,通过增加救援力量人数,可以加速任务完成,而实施挖掘作业,必须同时增加挖机和驾驶员的数量才能加速任务的完成。 另外,任务的执行时间与弹性分配的资源数量并不是线性关系,当达到最短任务执行时间后,无法继续通过分配资源的方式减少任务的执行时间,而继续增加资源只能增大任务完成的成本。例如,救援过程中,在狭窄范围内搜救幸存者时,不会因为投入更多搜救设备而提升任务执行效率。图2所示曲线表示该情境中,资源弹性分配的数量和任务执行时间、消耗成本之间的关系。因此本文所采用的弹性资源调度算法,仅考虑为任务分配小于或等于原本所需数量的资源,以平衡截止时间和成本的关系。 图2 弹性分配资源对任务的影响Fig.2 Impact of flexible resource allocation on tasks 针对RCTSP中产生的资源冲突问题,本文从两个角度出发进行资源冲突消解,避免在实际项目中因为资源冲突而产生连锁反应,或是造成更大混乱,在资源不充足时依然可以保证项目有序且高效推进。 3.1.1 基于贪心策略和拓扑结构的任务调度算法 本文提出一种基于贪心策略和拓扑结构的任务调度(task scheduling algorithm based on greedy strategy and topological structure, GSTS)算法。GSTS算法首先利用第2.1节中的方法,计算各个任务的关键度,通过关键度作为启发式信息,确定任务的优先级,之后基于任务流图和任务优先级进行任务调度。 图3 调整网络拓扑结构Fig.3 Adjusting the network topology GSTS算法在任务开始执行前进行对任务的调度,以贪心策略安排任务的开始时间,并通过提前调整网络结构避免了任务开始后产生的资源冲突。GSTS算法最终输出结果为经过调整的工作流图和各任务的开始时间点。 3.1.2 基于弹性资源的任务调度方法 当RCTSP中每个任务需求资源可弹性分配时,为解决任务调度中出现的资源冲突问题,同时降低整个项目的截止时间,提高资源的利用率,本文基于第2.3节提出的弹性资源下任务调度模型,提出了ER算法。 ER算法任务调度过程与任务执行交替展开,当有任务结束时,ER算法均会进行资源的重新分配。ER算法输出信息是为当前正在进行调度和已开始任务分配的资源量。 3.1.3 两种任务调度算法的比较 本文提出的GSTS算法和ER算法分别适用于任务资源不能进行弹性分配和可以进行弹性分配的两种情景,此外GSTS算法是得到任务调度方案和新的工作流图后开始任务的执行,而ER算法则是任务调度和任务执行工作并行,未来可以实现动态任务的调度。 针对资源冲突下任务调度问题,结合第3.1节所阐述的任务调度算法,在已经确定任务工作流图的情况下,通过设计相应的任务调度算法来辅助任务调度决策,为了实现在资源约束条件下尽可能早地完成所有任务,本文设计的任务调度算法框架描述如下。 步骤 1基于工作流图和项目截止时间,递推得到每个任务的最早开始时间和最晚开始时间。 步骤 2建立一个用来维护等待调度任务的列表Start-List,并将工作流图的开始任务加入。 步骤 3更新待调度任务列表StartList中的任务顺序。 步骤 4取出StartList中的第一个任务,判断是否满足资源约束条件,若满足进行步骤5,若不满足则进行步骤6。 步骤 5根据取出任务的所需资源、执行时间,占用系统中资源,并标记任务完成时间戳,加入待完成任务列表EndList,进入步骤7。 步骤 6判断是否产生资源冲突,是则进入任务调度算法。 步骤 7返回步骤4,直到完成StartList中任务的遍历。 步骤 8推进时间到EndList中最早完成的任务。 步骤 9释放已完成任务所占用的资源,并将其后继任务加入StartList。 步骤 10判断出口任务是否完成,否则进入任务调度算法。 步骤 11判断截止时间是否小于预期时间,是则成功完成任务调度,否则任务调度失败。 整个算法框架的流程图如图4所示。 图4 任务调度算法流程图Fig.4 Task scheduling algorithm flowchart 地震发生后,现场具有复杂性和不确定性,震后救援涉及全社会、多部门的合作,需要对参与人员和相关资源进行准确协调。地震救援的任务包括救援队伍机动、道路疏通、现场搜索、伤员救护等多个方面,无法确保获取充足的任务所需资源。因此,地震救援任务调度可能直接影响地震救援能否按期完成,关系到是否可以有效减少生命和财产的损失[26-27]。本文将一次地震救援案例作为验证任务调度算法的算例,验证本文提出的任务调度算法的效果。 地震救援任务可以分为准备阶段、机动阶段、救援阶段、撤离阶段和总结阶段,每个阶段都有相关的典型任务,各个任务的参数及关联关系可以表示为如图5所示的工作流图。 图5 地震救援任务工作流图示例Fig.5 Example of an earthquake rescue mission workflow diagram 本案例中考虑的资源只考虑人力资源和救援器械两种类型,人员和救援器械的总数分别为100和20。各个任务消耗的资源量和所需要的执行时间如表1所示。 表1 地震救援任务相关属性 将案例的相关数据输入算法,式(6)中η、λ、μ、σ1、σ2分别取2、5、0.5、0.1、0.5,通过评估函数计算得到各个任务的关键度,如表1所示。 对上述案例,在资源约束条件下,严格按照任务所需要的资源量进行分配,此条件下最优的任务调度路径,如图6中甘特图A所示。并分别使用本文提出的两种任务调度算法:GSTS算法可以得到图6中甘特图B所示的结果。通过增加任务b到任务e和任务f到任务g对应节点的边(如图6中点横线所示),添加新的约束可以完成对资源冲突消解。ER算法的结果如图6中甘特图C所示,其中白色部分为对应任务在资源不足的条件下开始。从对给定的地震救援案例分别使用GSTS算法和ER算法进行调度的结果来看,GSTS算法的任务截止时间仅比严格任务资源分配条件下最优解(78 h)多2 h,ER算法则将任务截止时间压缩到了68 h。 图6 任务调度结果的甘特图表示Fig.6 Gantt chart representation of task scheduling results RCTSP建模和求解方法主要分为启发式算法和元启发算法两大类[15,23-24,28-31]。针对两类算法,从每一类中选取一种较有代表性的算法与本文提出的算法进行对比,分别是以最大资源工作容量(greatest resource work content, GRWC)作为规则的启发式算法[30]和遗传算法[31](genetic algorithm,GA)。 为了使得实验结果更具有普遍性,利用随机生成100个允许弹性分配任务资源的算例,进行对比试验。各算例分别使用4种算法,得到项目的平均截止时间、人员利用率、救援器械利用率,各个量平均值直方图并标注标准差误差线如图7所示。4种算法均采用C++编码,在Intel Core i5-6300HQ的处理器上以2.3 GHz的速度运行,各个算法的运行时间如表2所示。 表2 不同算法运行时间 从图7中对比实验结果可以看出ER算法由于采用了弹性资源进行调度,平均截止时间、资源利用率都高于两种典型算法,其中平均截止时间作为调度问题的关键性指标,比GA和GRWC算法分别降低了7.7%和11.4%,资源利用率也都存在一定程度的提高。而本文提出的GSTS算法,对比将任务时间和消耗资源作为启发式信息的GRWC算法,截止时间下降了2.9%,两项资源的利用率分别提高了2.7%、2.8%,而对比GA,GSTS算法的性能略有劣势,但GSTS算法的时间复杂度明显小于GA,更能适应如地震救援等时间紧迫的调度情景,同时对比GA也更容易扩充节点,来应对未来的动态任务调度问题。 图7 算例分别使用各种算法所得结果对比Fig.7 Comparison of results obtained by using various algorithmsfor calculation examples 使用100个算例对比ER算法和GSTS算法,从结果来看,ER算法在85%的算例中有更低的截止时间。如果各个算例中资源不能进行弹性分配,ER算法则会退化成以任务先后顺序为优先级的算法。所得结果如图8所示。 图8 任务资源不能弹性分配条件下使用各种算法所得结果对比Fig.8 Comparison of results obtained by using various algorithms under the condition that task resources cannot be allocated flexibly 可以看出,GSTS算法在任务资源不能弹性分配时取得效果更优。GSTS算法为任务调度与任务执行串行,ER算法为任务调度与任务执行并行,并且由于ER算法需要频繁进行资源的重分配,在实际应用中可能会产生更高的成本,因此需要根据现实情况需求,来合理选择资源约束条件下的任务调度算法。 通过实验结果可以看出,本文提出的任务调度算法,基于工作流图解决了RCPSP,对比同类型算法有一定的优越性。同时可以适用于地震救援问题,实现资源冲突的消解,使得地震救援活动尽可能快地完成。 本文基于工作流图,综合地震灾后救援的特点,对资源约束条件下任务调度问题进行了研究。本文选用工作流模型更好地描述了地震救援中各项任务之间的联系及任务调度的过程,基于资源约束条件下任务调度框架提出了两种任务调度方法:GSTS算法适用于任务资源必须符合需求的情景,使用评估函数估计任务关键度,具有计算简便,信息综合程度高的特点,利用贪心策略和改变工作流拓扑关系的方法实现资源冲突消解和任务调度;ER算法从弹性资源调度的角度出发,提高了任务截止时间和资源利用率。两类算法和同类算法相比具有一定的优势,存在各自适合的情景,并与本文提出的地震情景相适应。 本文未来的工作主要从以下几个方面开展:研究本文提出的任务调度算法在动态情景中的应用,提升算法的动态性能;进一步明确资源约束条件下项目调度问题的内在机理,针对不同运用场景的不同特征,优化调整现有模型和任务调度算法;继续优化资源约束下任务调度算法的性能,使得在有限时间内可以达到或更接近理论最优解。2.2 资源约束条件下任务调度
2.3 弹性资源条件下任务调度
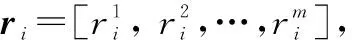
3 算法介绍
3.1 实现资源冲突消解的任务调度算法
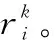

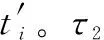
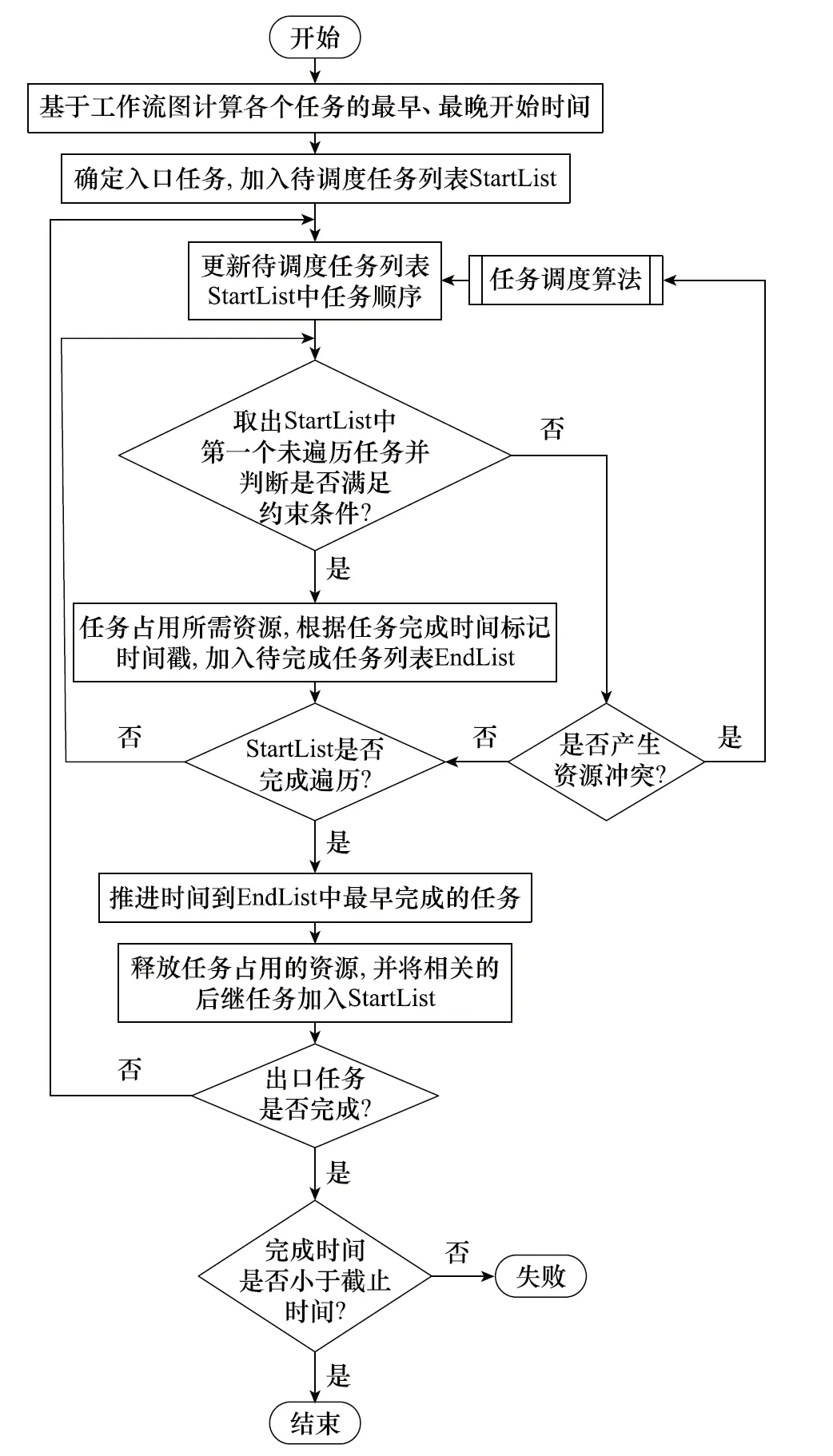
3.2 资源冲突下任务调度算法框架
4 案例分析
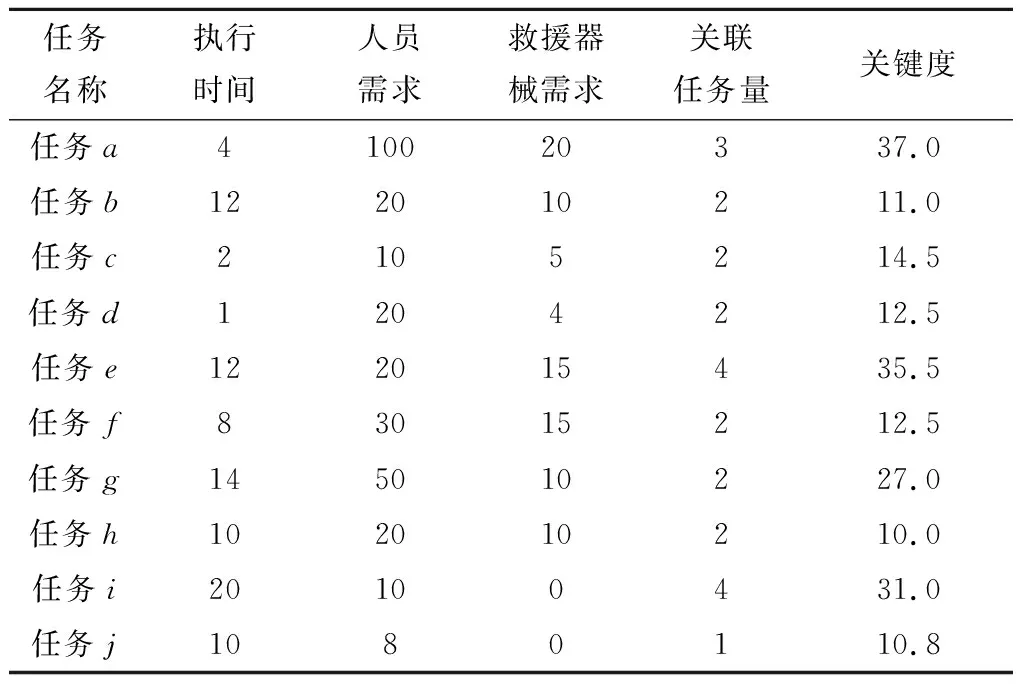
4.1 案例背景
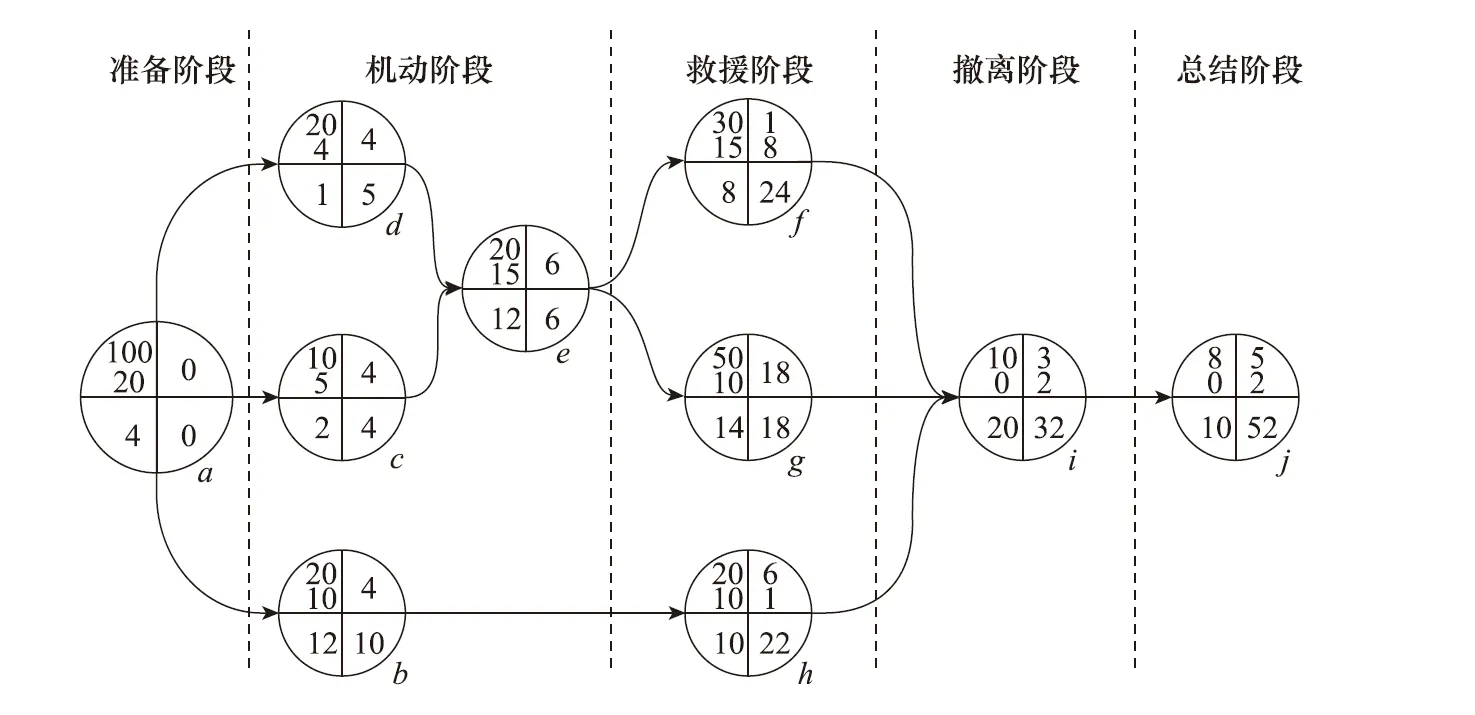
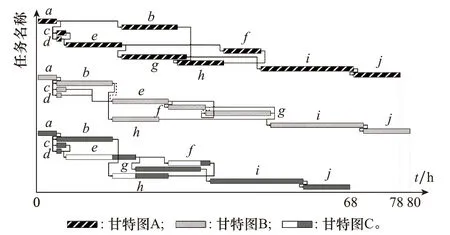
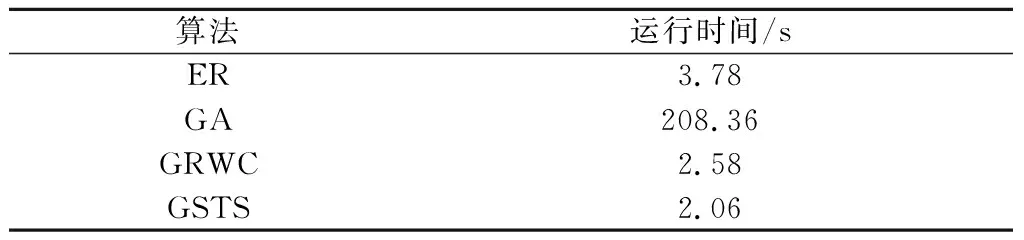
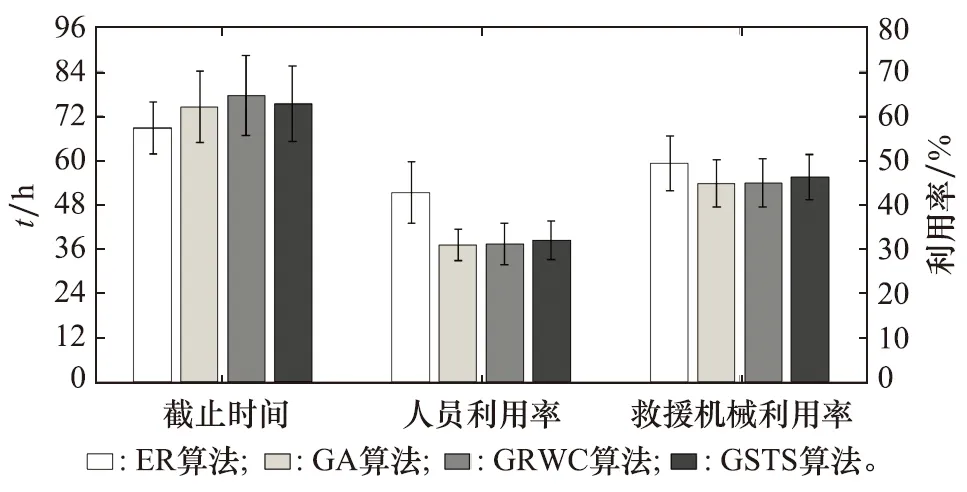
4.2 实验验证
5 结 论
