洛伦兹力磁悬浮织针驱动器设计与仿真

刘泽旭， 胥光申， 盛晓超， 代欣怡

(1. 西安工程大学 机电工程学院， 陕西 西安 710048； 2. 西安市现代智能纺织装备重点实验室， 陕西 西安 710048)

传统的针织机械利用织针、提花片、三角、沉降片与选针器等将纱线编织成针织物。织针编织动作由三角轨迹决定，其花型单一、更改复杂；并且由于存在刚性接触，传统机械驱动织针会产生较大的能量损耗、冲击和振动[1-2]，影响织针寿命和针织物品质。目前传统针织设备中三角、选针器以及织针的设计趋于最优，提升核心性能将付出越来越高的成本代价，因此对新型织针驱动的研究也越来越迫切。

近年来新型织针驱动研究主要有2个方面。直线电动机驱动织针：张森林等[3]提出用直线电动机替换电子提花机选针器，能简化织针驱动结构，减少磨损并提高工作效率；范良志等[4-5]提出一种超薄直线电动机驱动电织针，其结构布置与文献[3]提出的方案相反，并对电动机主要参数进行了设计；刘凯等[6]将动圈式U型直线电动机用于袜机织针驱动，通过对电动机磁场、磁感、电流密度等分析验证了驱动可行性，但是利用直线电动机驱动织针成本较高、控制系统复杂，目前的研究还处于理论阶段且缺少样机。磁悬浮驱动织针：吴晓光等[7-9]将磁悬浮技术与织针驱动结合提出单线圈磁阻式悬浮织针驱动模型，可以代替传统针织机械驱动系统的三角、选针器等结构，由于无刚性接触，能大幅度降低摩擦损耗及噪声，提高机械运行速度；万道玉等[10]提出了双曲线电磁悬浮织针驱动模型，采用智能算法将线圈轮廓优化为双曲线型，可以有效提高驱动力与磁场稳定性；游良风[11]提出由3个线圈组成的多级电磁悬浮织针驱动模型，可以实现大行程、多位置悬停，完成“五功位”编织动作。上述磁悬浮织针驱动模型皆为磁阻力驱动，其驱动力与电流、气隙(位移)呈非线性关系，模型控制较为复杂。

本文将洛伦兹力磁悬浮技术引入到针织机械中，提出一种洛伦兹力型磁悬浮织针驱动器模型，可以替代传统织针驱动部件(三角、提花片和选针器等)，使织针驱动几乎无刚性接触，消除织针驱动存在的振动、摩擦与冲击，以期编织轨迹控制更加简单、精确。

1 织针驱动原理与结构

1.1 洛伦兹力磁悬浮织针驱动器原理

磁悬浮技术可根据驱动原理分成磁阻力型和洛伦兹力型[12-13]，其中洛伦兹力型由于力与电流有较好的线性关系，具有响应迅速、模型简单以及控制精度高的优点。洛伦兹力表达式为

f=qvB

(1)

式中：f为洛伦兹力，N；q为电荷，C；v为电荷运动速度，m/s；B为磁感应强度，T。

由于电流是大量电荷运动形成，洛伦兹力在宏观电流上表现为安培力，其表达式为

F=IdlB

(2)

式中：F为安培力，N；Idl为一段电流元，A·m。

基于磁场中的电荷受到洛伦兹力的作用，提出如图1所示的洛伦兹力磁悬浮织针驱动器原理。利用4个永磁体布置2个近似均匀而磁感应强度相反的磁场，其中上侧磁场磁感应强度方向向右、下侧磁场磁感应强度方向向左；将一个方型线圈的上下两端导线置于2个磁场的有效范围内，给线圈通入电流使线圈上端导线电流流出、下端导线电流流入，则线圈受安培力作用；由于线圈上下两端的电流方向相反且磁场方向相反，线圈上下两端导线受到的安培力大小相等、方向均向上，若通入的电流反向，则线圈受向下的安培力；线圈两侧导线分布宽度大于永磁体宽度，所以两侧导线始终处于磁场的外部而不会受到力的作用，从而确保织针只有上下的直线运动。将织针固定在线圈上，则织针将在线圈所受到的安培力作用下运动，控制线圈电流即可控制织针动作。

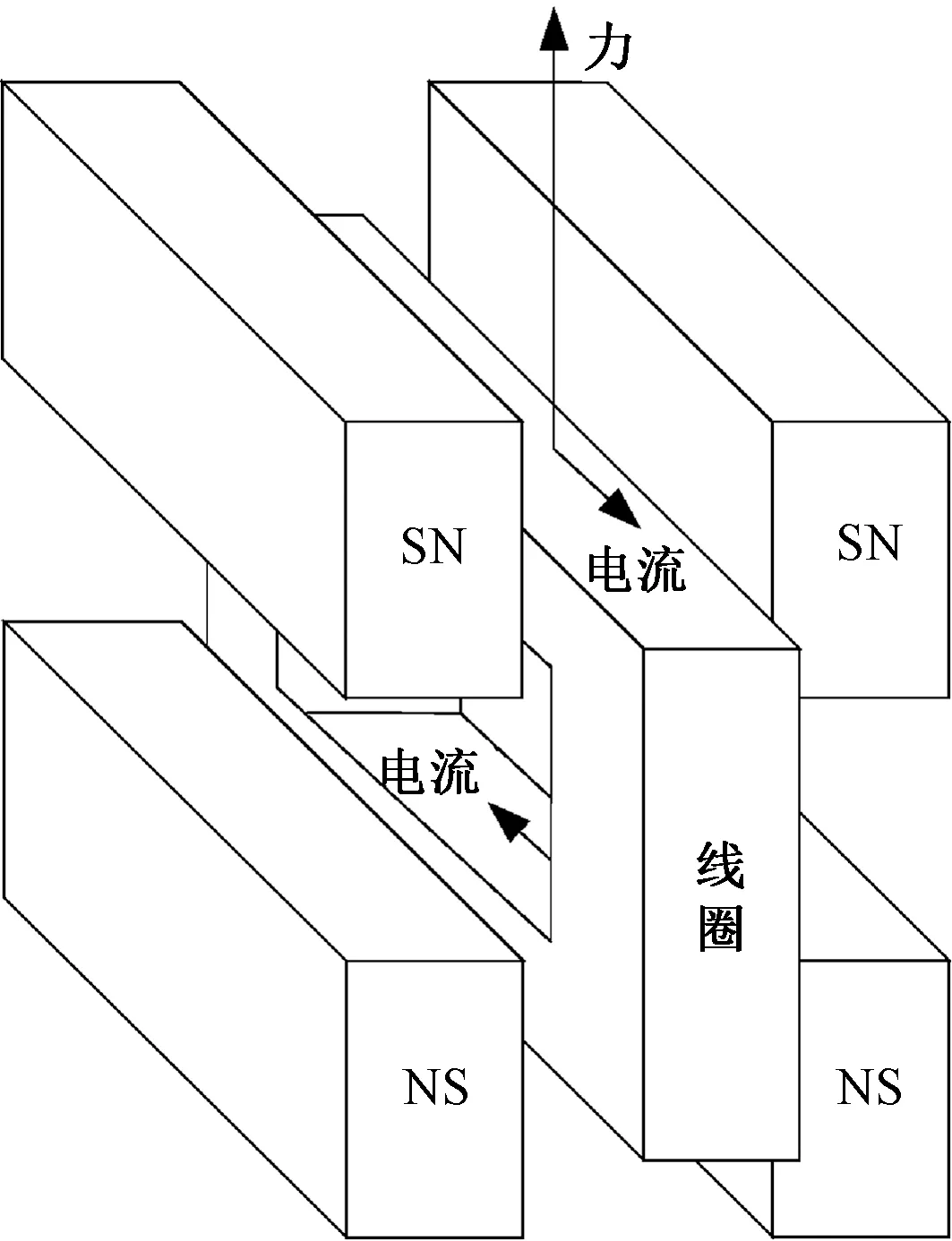
图1 洛伦兹力磁悬浮织针驱动器原理Fig.1 Principle of Lorentz force actuated maglev knitting needle actuator

1.2 洛伦兹力磁悬浮织针驱动器结构设计

洛伦兹力磁悬浮织针驱动器结构如图2所示。模型由线圈、织针、永磁体、位置传感器、磁轭、控制器和功率放大器等构成。

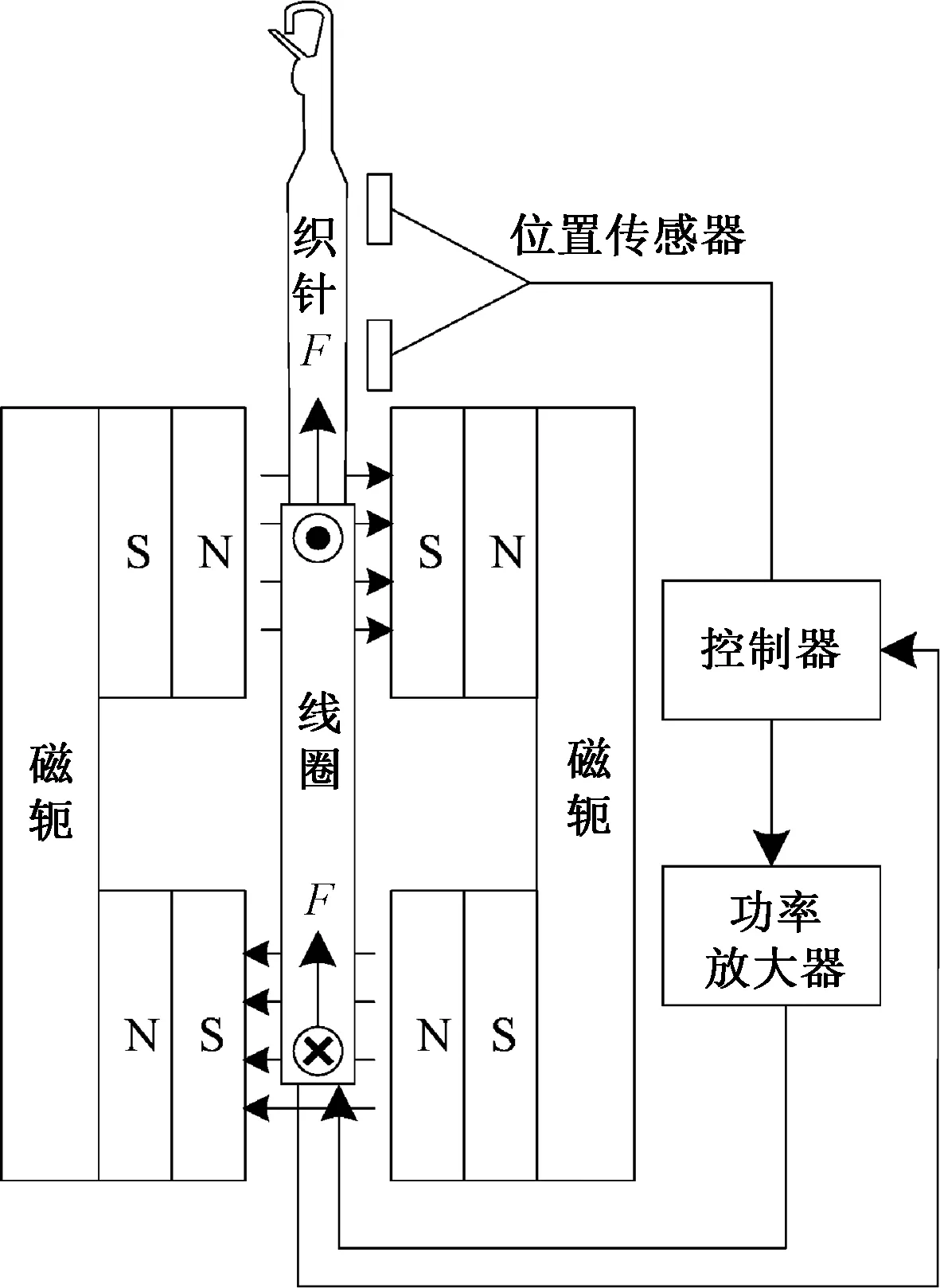
图2 洛伦兹力磁悬浮织针驱动器结构示意图Fig.2 Structure of Lorentz force actuated maglev knitting needle actuator

将4个正对的永磁体安装在2块磁轭上组成定子，使系统的磁路闭合，更高效利用磁场产生电磁力；织针固定在方型线圈上组成动子，并使线圈上下两端导线在运动过程中始终处于有效磁场范围内；当给线圈通入直流电后织针会产生位移，通过位置传感器实时采集织针位置信号，经过控制器分析运算后输出控制电流；控制电流再经过功率放大器放大后输入到线圈进行驱动，从而带动织针完成编织动作，整个系统为闭环控制系统。

在该方案下每个织针由电流控制独立运动，没有传统的选针动作，与之相关的选针器、提花片、挺针片等部件不再需要，织针驱动结构被简化。并且织针由线圈带动悬浮运动，整个过程没有三角造成的刚性冲击，从而织针的运动更平稳，控制精度更高，驱动结构磨损更小。

2 数学模型建立

2.1 受力分析

图3为系统整体受力分析图。动子运动过程中会受到电磁力、摩擦力、织针重力以及纱线张力的作用，动子受到的合力FH为

FH=F1+F2+Fz+f+G

(3)

式中：F1、F2为线圈上下两端产生的安培力，N；Fz为纱线张力，N；f为摩擦力，N；G为系统重力，N。

图3 模型受力分析图Fig.3 Model stress analysis.(a)Knitting needle rise; (b)Knitting needle drop

F1、F2是模型的驱动力，表达式为

F1=NI1LB1

(4)

F2=NI2LB2

(5)

式中：N为线圈的匝数；I1、I2为线圈上、下端电流，其大小相等、方向相反，A；L为磁场中线圈的有效长度，m；B1、B2为上、下磁场的磁感应强度，其大小相等、方向相反，T。

在该模型中稳恒磁场由永磁体提供，若忽略漏磁磁阻，其磁感应强度B1、B2大小可以由气隙磁感应强度表达式计算：

(6)

式中：B为B1或B2大小，T；Br为永磁体最大剩磁，T；h为永磁体厚度，m；δ为气隙宽度，m；Fc为磁动势，T/m；Sm为永磁体正对面积，m2；Rm为永磁体磁阻，H；Rδ为气隙磁阻，H。

式中，μ0为真空磁导率，4π×10-7H/m。

式(6)仅为近似计算使用，工程实际计算磁感应强度B较为复杂，通常采用电磁有限元软件进行仿真计算。

织针在运动过程中处于悬浮状态，除必要的径向支撑外几乎无刚性接触，纱线张力Fz为0.03～0.04 N，织针运动的摩擦力[14]约为0.000 2 N。因此，本文将织针在运动过程中受到的摩擦力f与纱线张力Fz的共同作用看作是系统的一个扰动力Fd，则系统的受力可简化为

FH=F1+F2+G+Fd

(7)

由此可知系统的平衡静止条件为

F1+F2=G+Fd

(8)

2.2 系统运动方程

将织针与线圈等效为一个质量块，根据式(7)和牛顿第二定律可得动子运动微分方程：

(9)

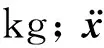
将式(4)、(5)代入式(9)，得到洛伦兹力磁悬浮织针驱动系统的运动方程:

(10)

3 模型电磁场有限元分析

3.1 电磁场建模与分析

洛伦兹力磁悬浮织针驱动器中由永磁体提供稳定磁场,使通电线圈在安培力作用下带动织针运动，模型磁场的分析可为力计算和控制过程提供依据。前期查阅资料发现,对永磁体磁场的建模和理论计算较为复杂，且忽略了材料非线性特性、漏磁等，因此本文采用ANSYS软件对模型电磁场进行分析，其计算精度高,适合模型初期的设计。

本文根据驱动原理，采用Plane13，四边形13节点单元进行二维平面静态磁场有限元模型分析。定义模型材料参数如下：空气相对磁导率为1.000；永磁体材料选钕铁硼，其剩磁为1.17 T，内禀矫顽力为422 000 A/m，相对磁导率为1.103；线圈匝数为250，相对磁导率为1.000；磁轭相对磁导率为4 000。

模型有限元网格如图4所示，模型中磁轭宽a=5 mm，高b=90 mm；永磁体宽c=10 mm，高d=40 mm；气隙宽度e=10 mm；线圈高f=6.5 mm，宽g=5 mm。对磁场有限元模型求解后，驱动器磁场有限元仿真如图5所示。

图4 磁场有限元网格划分Fig.4 Magnetic field finite element mesh generation

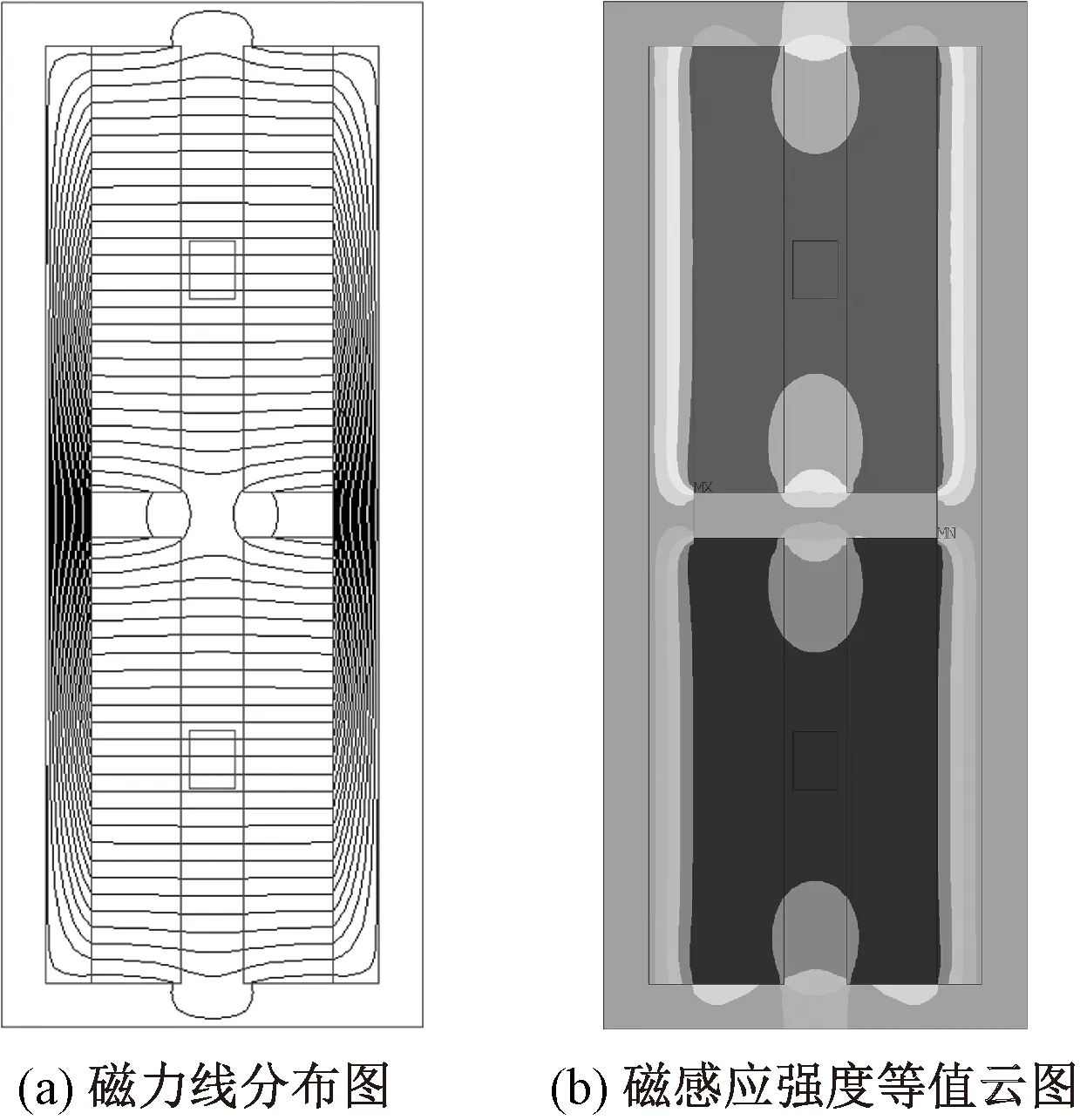
图5 磁场仿真结果Fig.5 Results of magnetic field simulation.(a)Magnetic lines distribution; (b)Magnetic flux density distribution

由图5可以看出，模型磁力线沿磁轭以及2组永磁体正对的气隙处闭合。这是因为磁轭的磁阻远小于空气，而磁力线沿磁阻最小的路径通过并闭合，设计结构时将永磁体安装在磁轭上，磁力线沿着设计的通路闭合，使漏磁较少。由于气隙处的磁力线均匀闭合，模型中2组永磁体正对区域内的磁感应强度分布也较为均匀。

定义模型最下侧为“零”位，模型气隙中部磁感应强度大小变化如图6所示，并且在14～26 mm及64～76 mm范围内曲线斜率几乎为“零”，其磁感应强度值也较为均匀，稳定在0.36 T左右。

图6 径向磁感应强度Fig.6 Radial magnetic induction intensity

给线圈通入1 A电流，线圈轴向有磁场对线圈产生的单位长度安培力为185.61 N/m；径向有永磁体对线圈产生的单位长度磁阻力为0.013 8 N/m，其较小可忽略。

3.2 驱动可行性分析

“三功位”织针的编织动作主要有成圈、集圈和浮线，根据传统驱动中三角轨迹和运行频率优化的单个磁悬浮织针运动轨迹如图7所示[15]。可见织针运动轨迹为：上升成圈—下降浮线—上升集圈—下降浮线。

图7 磁悬浮织针运动轨迹Fig.7 Motion trace of maglev knitting needle

整个轨迹的最大位移为上升成圈阶段，在7 ms内从0 mm上升至9 mm，则织针运动所需最大加速度为

(11)

式中：S为位移，m；t为时间，s。

假设织针与线圈整体质量为0.02 kg，磁场中导线有限长度为0.05 m，重力加速度为9.8 m/s2，扰动力Fd为0.05 N，则织针运动所需最大单位长度驱动力为

(12)

式中：F为所需最大驱动力，N；l为导线长度，mm。

由3.1小节可知，当给线圈通入1 A电流时可产生185.61 N/m的单位长度安培力，完全可以驱动织针完成编织动作。

4 控制器设计与仿真

4.1 控制系统建模

洛伦兹力磁悬浮织针驱动器的控制目标是保证线圈在驱动力和扰动的作用下能按照预计的轨迹运动。本文采用PID控制器进行闭环反馈控制，模型控制系统框图如图8所示。

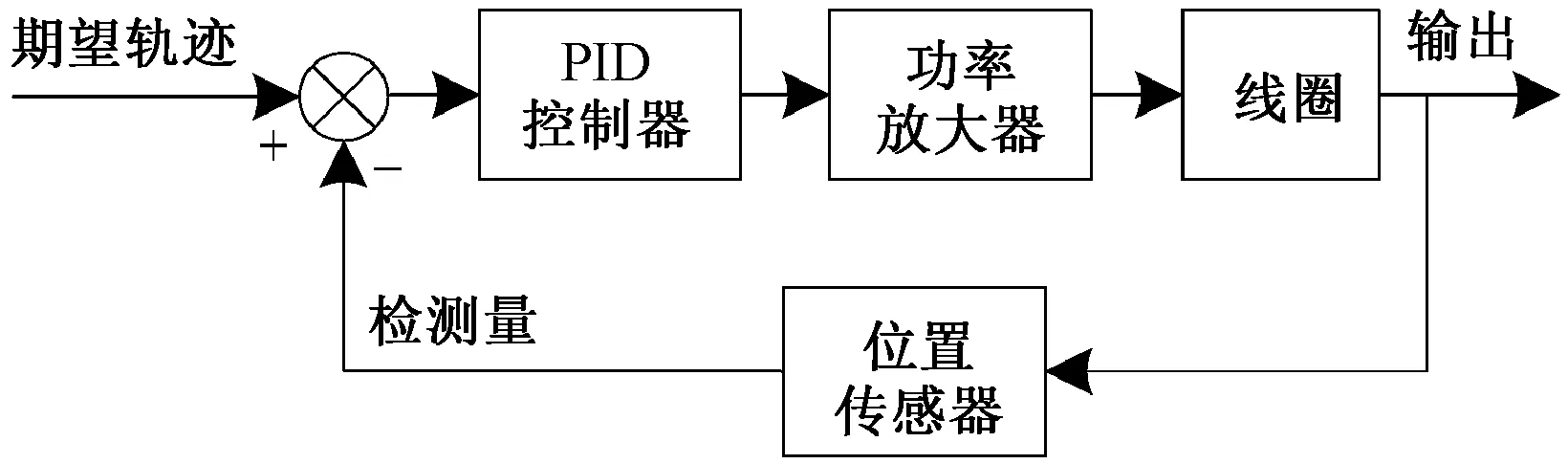
图8 洛伦兹力磁悬浮织针驱动器控制系统框图Fig.8 Block diagram of Lorentz force actuated maglev knitting needle actuator control system

系统先通过传感器采集线圈位置，然后与给定位移作差后经PID调节输出控制电流，控制电流再经功率放大后驱动线圈运动。

根据式(9)可得到系统传递函数：

(13)

模型的驱动力与织针位移为线性关系，根据图8所示框图在MatLab/Simulink环境下搭建的控制系统总体模型如图9所示。

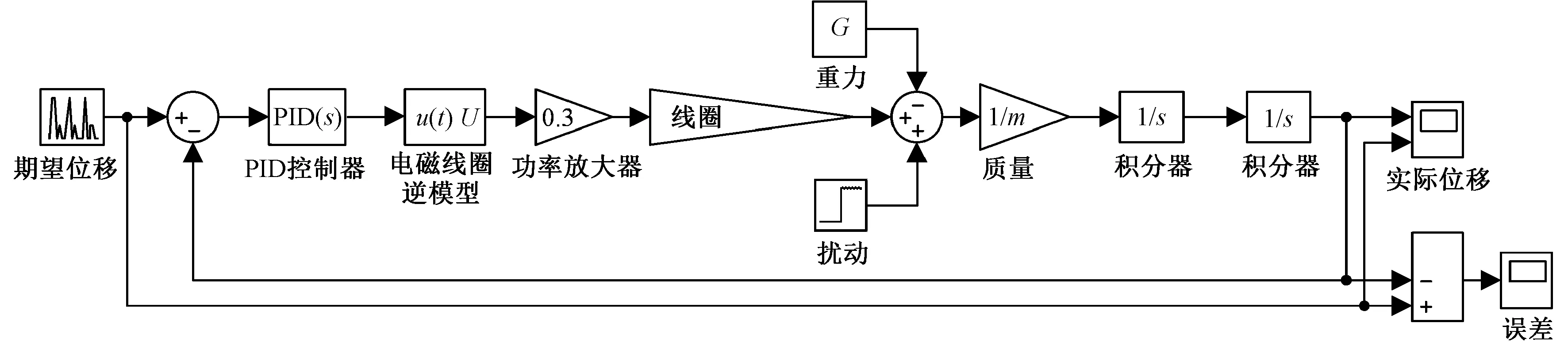
图9 控制系统总体模型Fig.9 Overall model of control system

4.2 控制系统仿真

如图9所示，根据期望轨迹与实际位移差值，PID控制器调节后输出控制信号u(t)；u(t)输入电磁线圈逆模型，经过运算后得到线圈电压U；电压U再经过放大后输出电流，使线圈产生安培力驱动织针运动。在该模型中考虑了重力和扰动的影响，在驱动力后增加了这2项，力经过传递函数后输出为实际位移。

PID控制器参数设置为Kp=180，Ki=40，Kd=40；线圈匝数为250，磁场中有效长度为0.05 mm；模型求解算法为ode23，仿真步长为0.001；设置期望位移为图7所示的“三功位”织针编织轨迹，其仿真结果如图10所示。

图10(a)示出织针位移仿真结果。织针位移平稳，响应迅速，轨迹与预期目标一致。由此可以得出，该控制系统可以控制线圈完成成圈、集圈和浮线动作。图10(b)示出织针位移误差仿真结果。位移误差在±3.5 μm之间，系统控制的精度可达微米级。

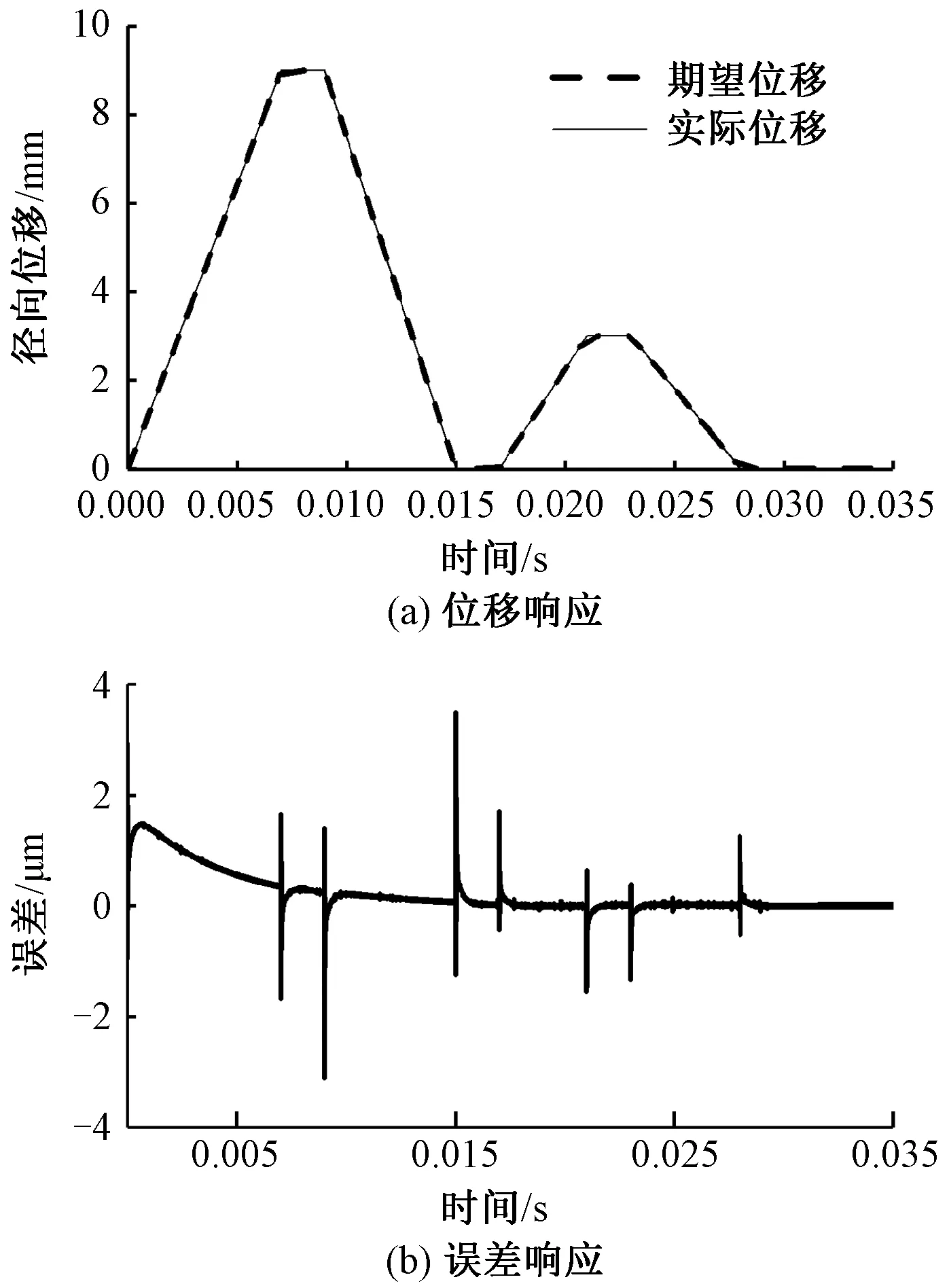
图10 控制系统仿真响应Fig.10 Curve of control system response.(a)Displacement response; (b)Displacement error response

5 实验验证

为验证该驱动原理与模型的正确性，需搭建实物平台测试其是否能驱动织针运动并使织针达到编织高度。根据驱动原理与结构制作洛伦兹力磁悬浮织针驱动器样机，如图11所示。

图11 洛伦兹力磁悬浮织针驱动器样机Fig.11 Lorentz force actuated maglev knitting needle actuator prototype

利用特斯拉计测量图6曲线中“零”斜率区域的驱动器样机磁感应强度，测量结果为0.361 T，与图6所示电磁有限元仿真结果吻合，则该驱动器样机结构与材料特性完全符合理论设计，因此,3.2小节可行性分析成立，该驱动器可以满足织针“三功位”编织动作驱动力需求。

为了更好地测试驱动器性能，选择阶跃信号进行测试。首先阶跃信号可以验证系统是否能够正常驱动，并对其进行运动控制；其次可以验证织针是否能上升到编织要求的最大行程，并测试系统的稳态控制精度范围。因此，将控制系统模型中的织针期望轨迹设定为阶跃信号，目标位移设定为成圈、集圈中较大的集圈编织高度，使织针在第3秒上升至9 mm高度。随后将模型烧录到Links-RT半实物仿真平台中对织针运行状态进行控制，织针位移由激光位移传感器进行检测并反馈给控制平台，实验结果如图12所示。

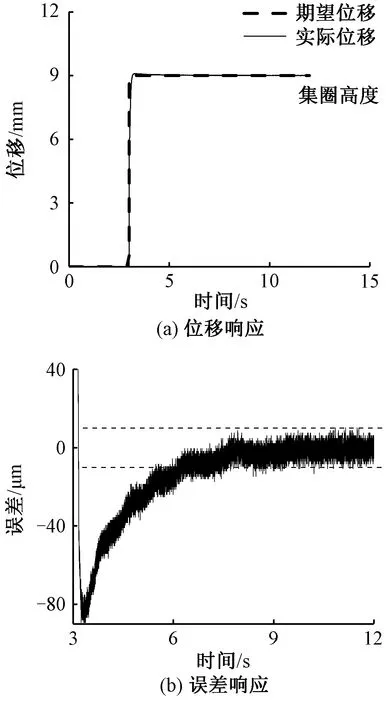
图12 实物实验结果Fig.12 Results of physical experiment.(a)Displacement response; (b)Displacement error response

图12(a)示出织针位移响应，织针实际位移在第3秒上升至9 mm并保持，响应迅速，过程平稳无振荡，稳态时系统位移稳定在9 mm附近；图12(b)示出织针位移误差响应，初始误差为90 μm，随后在PID闭环调节下误差收敛，稳态时误差值在±10 μm之间波动。由实物实验结果可以看出：该驱动器驱动原理与结构合理可行，可以驱动织针平稳运动并使织针保持在集圈高度，满足了编织最大行程需求；驱动器在PID控制下稳态误差范围为±10 μm，表明该线性洛伦兹力磁悬浮织针驱动系统控制精度较高，可达到微米级。

6 结 论

本文建立了洛伦兹力磁悬浮织针驱动器数学模型，模型驱动力与电流为线性关系；利用ANSYS软件对模型磁场、电磁力进行分析，通过计算验证了驱动可行性；设计PID控制器并在MatLab/Simulink中搭建系统控制模型，仿真结果显示织针轨迹可以完成“三功位”编织动作，仿真误差在±3.5 μm之间。实物实验结果显示，该驱动器可以驱动织针达到编织高度，且运动平稳，误差在±10 μm之间。综上，洛伦兹力磁悬浮织针驱动器可以替代传统织针驱动结构实现织针编织功能，且系统为线性系统，控制简单、精度可达微米级。该模型为消除传统三角驱动的摩擦、振动和冲击的研究提供了新的思路和方法。

FZXB