数形结合思想的精髓在于规律呼应

史秋平

[摘 要]数形结合不是简单地用代数式表示几何图形或者用几何图形来反映数量关系，而是数量内部的规律与图形内部的规律高度对应统一。图形的深刻规律要用代数式才能揭示出来，代数式的运算规律很抽象，要借助直观的图形拼摆演示才能做出合理解释。

[关键词]数形结合;规律;教学

[中图分类号] G623.5[文献标识码] A[文章编号] 1007-9068（2021）32-0073-02

教学内容为第十一册第八章第107页例1、第108页“做一做”栏目、练习二十1、2题。教学目标主要有：通过观察研究，让学生探明数形之间的关联，能根据图形的变化看出数量的变化;引导学生总结规律，并应用规律进行运算。教学重点：探查数形之间的关系，并能用图形的变化规律揭示数字的变化规律。教学难点：发掘规律并验证这个规律。

一、课前导入，新知铺垫

【教学片段】

笔者先带学生看电子白板，粗略回顾旧知：1×1可以简写成[12]（读作1的平方），[12]=1，那么以此类推就有3×3=[32]=9，4×4=[42]=16。并随机问学生：“一个数的平方等于多少？”

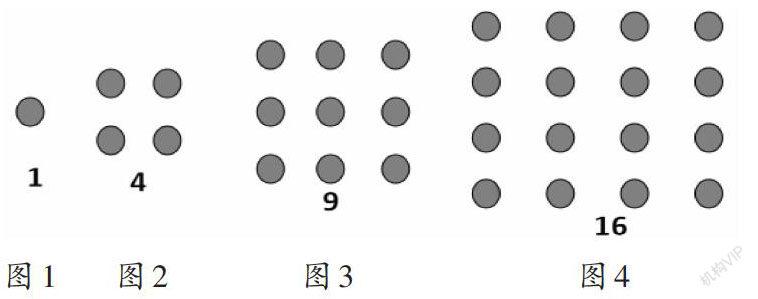
师：探寻规律。先看图再观察分析数字变化情况，推断出第5个图中圆点的个数。

师：你是怎么推的？你能够延续此法，推断出第6个图中圆点的个数吗？你运用了什么方法推断？（学生发现圆点的排列规律）

师：像这样，图形与数字严格对应，相应变化，呈现出明显的规律，运用这个规律就可以推测出后续将会出现的图形和数字，这类题目在数学里统称为数形结合。今天大家一起探寻数形结合里的秘密。

笔者板书课题：数形结合。（学生齐读课题）

数形结合有的时候是根据数量与图形的对照关系，通过二者的相互印证，将抽象的数字与直观的图形联合，并以此来分析解决问题的思想方法。

二、探究新知，发现规律

1.观察、探究、概括

【教学片段】

师：现在老师就带大家一探乾坤。

师（呈现1个长方形，如图5）：数目是几？改用平方数表示，写成多少？

生1：1=[12]。

师：接着看，扩展这个图，增加了3个同样大小的长方形，增加的长方形呈“L”字形，与原来的长方形组成一个两行两列的“田”字格（如图6），此时长方形的总数如何计算？

生2：1+3=4。

师：改写成平方数如何表示？

生3：[22]。

师：每次增加的长方形都呈“L”字形，此时长方形的个数如何计算？（如图7）

生4：1+3+5=[33]。

师：小组内讨论一下，能根据图5、图6、图7推断出第4个图形的排布情况和长方形个数吗？请画出草图，写出算式。

（学生讨论，在草稿纸上画出草图，并写出算式。教师巡查，然后请人叙述画图过程并口述算式）

师：通过认真思考，大家发现了一些浅显的规律，其实还有一些深刻的规律。大家不妨再找一找。

2.小组分工，找规律

【教学片段】

师：大家这么厉害，后面几个规律就留给你们独立寻找了，敢接招吗？不可莽撞，要按照老师的指示寻找规律，分工合作，并将概括出的规律写进小组实验记录单中。如遇阻，可以向其他小组或老师求助。

笔者分工：A组研究第一个问题，B组研究第二个问题，C组研究第三个问题，D组完成第四个问题。

各小组完成任务后，可以帮助其他小组。最后集中展示交流。

学生探讨问题，笔者巡视指导，并及时点拨。

【设计说明】

数形结合是新增内容。如果彻底放手让学生自主探寻规律，恐怕学生会有负担，所以才有了笔者“引路”，学生“探路”。笔者一边出示图形，一边提问，学生对比分析出图形与数量的对应关系，笔者“搀扶”着学生慢慢走，推断后续图形，调动学生的联想能力和推理能力，由形象到抽象，由浅显到深刻，循序渐进。笔者“松手”，学生“上手”，学生自己探究，互相交流讨论、深刻反思，既能在探究中体验知识生成的过程，又能体会到合作的意义。

3.小组汇报，概括规律

【教学片段】

问题1：每次增加的“L”形图中包含长方形的个数有什么变化规律？长方形总数与增加次数有什么关系？增加次数与最终图形的边长有什么关系？

师：等式左边加法的图形意义是什么？你能举例说明吗？

生：等式左边算式的图形意义是基础个数（右上角1个）和逐次增加的“L”形图中长方形个数的总数。

问题2：等式左边加法算式的和与最终定型的图中长方形的行数（列数）有什么关系？

师：最终定型的图中，每行（每列）长方形个数的平方表示什么意义？举例说明。

生：等式左边加法算式的和与最终定型的图中每行长方形个数的平方相等。

问题3：等式左边的加数是按照什么规律排列的？

生：等式左边的加法算式中，加数是连续的奇数。

问题4：等式左边加数个数与等式右边乘方数有什么关联？

师：仔细观察上述等式，从哪里起步？这个规律如何表述？

生：从自然数1开始，几个连续奇数的和等于加数数量的平方。

【设计说明】

学生概括出的规律只是初步的规律，是否具有普遍性，还需要检验。学生展示汇报，既是一种自我肯定，也是接受监督和检验的过程。同时，在此过程中，学生的思维过程还充分暴露出来，接受评价，从而不断完善自己的思维。

三、课后反思

数形结合的主要目的是“以形助数”（将代数问题转化为图形来研究）或“以数助形”（利用算式或者运算规律来概括图形组合规律），把抽象的算式与形象的图形融为一体，也就是将抽象思维与形象思维有机结合起来，是初等数学中常见、常用的思想方法。在教学中，笔者主要靠回顾旧知来探查规律，分步完成。

这节课的亮点有几个方面：

1.数学直观化，概念生成及时。数形结合其实就是一种改版的找规律，只不过这种规律需要用算式表达。上课伊始，笔者并没有给学生施压，而是通过复习旧知来暖场，消除学生的戒心，化解他们的焦虑和抵触情绪。

2.注重知识生成，学生参与探究。本节课的重点是让学生会用图形与算式的规律互相印证、理解和阐述，而这些规律很隐蔽，难以察觉，甚至难以用语言描述。为了破解这个难点，笔者让学生以小组合作的方式开展学习：小组推测后续图案，探究规律，展示汇报。教师引导知识生成而不是灌输知识，学生有很大自由度，认知从模糊到清晰，思绪从混沌到清明。

3.注重稳扎稳打。学生首次接触数形结合，再加上规律隐晦，欲速不达，笔者并没有着急，从“引路”到“搀扶”，再到“松手”，让学生一步一个脚印，稳扎稳打。

4.尊重学生表达。每个学生的思维存在差异性，看问题的视角也不一样，如果学生的看法与教师不同，教师要善于倾听学生的想法，给他们充分申辩的机会，学生也许在辯论中就能发现自己的错误。

这节课的教学也有些许不足：

1.“双备”（备教材、备学生）不合拍。顾此失彼，只顾钻研课本，没有了解学生，高估学生，导致学生对前两个规律的理解模糊。

2.达不到超越教材、灵活运用教材的程度。本节课中，前两个规律的表述特别拗口，单看字面意思很难领会，必须结合前期的观察分析，这也在无形中给学生设置了障碍。笔者认识到了自己做得不足的地方：没有事先组织好语言，对教材加工不到位。

3.评价语言干瘪乏味。笔者觉得学生自己会分辨是非好坏，鼓励是多余的，其实这是一种误解，学生需要更多鼓励和支持。

总之，这节课笔者有得有失，今后的教学中一定会不断改进修正，不断总结、提升，扎扎实实把每一节课上好。

（责编 黄 露）