机器学习算法在电力贫困用户识别中的应用

毛秋云,李 璟,毕凤娟,潘一洲,蔡 慧,郭 倩,卢子萌

(1.中国计量大学 机电工程学院,浙江 杭州 310018;2.浙江华云信息科技有限公司,浙江 杭州 310012)

随着社会的发展,电网的覆盖面越来越广。电力企业拥有大量的用户用电数据,包括用户的年用电量、日用电量、缴费方式等。在这些数据之中隐藏着用户的用电特性信息,能够反映用户的类型和用电习惯[1-2]。然而由于电力用户数量庞大,这些数据往往十分繁杂多样,难以直观地看出用户特性。而对这些数据进行处理,进而提取出有价值的信息,成为当前的一大研究发展趋势。通过大数据分类方法可对这些数据进行分析分类,根据用户的用电习惯的不同将用户分为多个类别,得到不同的用户用电分类模型。常用于电力系统数据分析的方法有逻辑回归、支持向量机、决策树、神经网络等[3-6]。应用于预测分类的常用方法有神经网络、K-means聚类和模糊C均值法等,其中采用模糊C均值进行分类容易陷入局部最优的问题[7-9]。文献[10]将逻辑回归与支持向量机应用于某项指标敏感性评价,得到了较好的分类结果。文献[11]使用的支持向量机模型在电力系统故障分类方面表现出了比决策树和k近邻更好的分类特性。

近年来政府提出动员全党全国全社会力量,坚持精准扶贫、精准脱贫。贫困用户的精确识别就是精准扶贫的前提。传统的贫困用户识别采用实地走访方式进行贫困状况调查,该方式对人力资源要求高,走访时间长,存在信息延迟性且有走访对象表述不真实的隐患。而使用机器学习算法结合大数据进行分析越来越广泛地被应用于精准扶贫研究[12-14]。通过机器学习算法基于用户电量数据对贫困用户进行在线识别,相较传统调查方法更加准确,更具时效性。

本文的研究内容是基于用户电量信息分别采用支持向量机、逻辑回归和神经网络方法对电力用户进行分类,对三种分类方法的分类效果进行分析比较。该研究能够面向贫困用户进行分类,找出更适用于电力用户分类的方法。同时该研究通过分类定位出贫困用户,为精准帮扶提供基础,提高工作效率,具有一定的社会价值。

1 数据来源与提取

本文的数据来源是浙江省某地区3 591户家庭用户一年360 d的日用电量。即每个用户作为一个样本,共3 591个样本,每个样本包含了360个日用电量值。其中958户样本为贫困用户,2 633户样本为非贫困用户。贫困用户的样本标签判定依据为该户是否持有政府开具的低保证明。分类目标是对该地区用户进行贫困与非贫困用户识别。整体贫困用户与非贫困用户的分布比例接近1∶2.7,样本分布不平衡。在对数据进行分类时,需要根据特征量来进行区分。一个合适的特征量能够体现出数据本身的特点,且能准确反映出不同类型数据之间的差别。因此特征量的选取十分关键,当特征量过多时,会导致分类过程过于复杂;而特征量过少时,会导致分类结果不够精确。进行贫困用户识别时需要先对以上用户用电信息进行有效特征提取,再对提取的特征量进行处理后用于用户识别。

在贫困用户和非贫困用户中各随机选取两个用户,绘制四个用户的年用电量曲线如图1。

图1 电力用户年用电量对比Figure 1 Annual power consumption comparison of power users

图1(a)和图1(b)各选取了一个贫困用户和一个非贫困用户进行对比。由图1(a)中可见,非贫困用户的日最高用电量可达24度,日用电量主要分布于5度上下,日平均用电量为6.33度;贫困用户年用电量的整体分布情况低于非贫困用户,最高用电量达到8度,日用电量主要分布在0～5度之间,日平均用电量为3.29度。

同理由图1(b)中可见,非贫困用户的日最高用电量可达17度,日用电量主要分布于5度上下,日平均用电量为5.53度;贫困用户年用电量的整体分布情况低于非贫困用户,最高用电量达到10度,日用电量主要分布在0～4度之间,日平均用电量为2.61度。

由以上分析可知,一年中贫困用户的日用电量整体低于非贫困用户。原因是贫困用户在自身经济条件限制下,用电习惯较为节省,且家用电器不多。所以贫困用户的日用电量均值普遍低于非贫困用户。

从用电量变化情况来看,两类用户在春节期间和夏季七八月份均出现了用电高峰。其中夏季的用电量变化情况较为明显,原因是在气温变化影响下,用户使用了空调、电风扇和取暖器等较大功率的制冷制热家用电器。但贫困用户的家用电器种类往往较少,使用频率相比非贫困用户而言也更低。在日常用电活动中用电量的波动程度不会太大,相较非贫困用户更加平稳,因而年用电量方差会小于非贫困用户。另外,贫困用户的用电量整体波动范围也会小于非贫困用户,相应的年用电量极值差会较小。

从数据细节变化方面来看,对数据进行差分处理后取方差和平均值,能够更加明显地体现出数据细节的变化。而从数据整体变化方面来看,冬季和夏季会出现用电高峰,波形前后会有明显的上升下降。为了更加明显地呈现出数据的整体变化趋势,降低噪声影响,首先对年用电量进行滤波,选取滤波周期为15 d,该周期长度能使数据不仅能明显地体现出整体变化而且不会丢失过多的细节信息,然后对滤波后的数据取方差。图2为图1数据进行滤波后的结果,可见滤波后的数据降低了噪声的影响,使得数据的整体变化趋势更加明显。

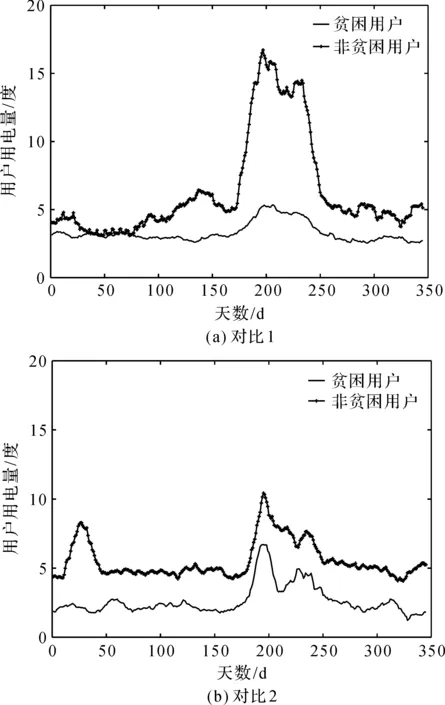
图2 滤波后电力用户年用电量对比Figure 2 Comparison of annual electricity consumption of power users after filtering

图2(a)中贫困用户的用电量方差为0.72,非贫困用户的用电量方差为3.72。图2(b)中贫困用户的用电量方差为1.07,非贫困用户的用电量方差为1.35。从用电量整体变化情况上来看,非贫困用户的用电量方差普遍高于贫困用户。

同时,对一年的日用电量提取四分位数也可反映数据的变化趋势。四分位数通过把所有数值由小到大排列并分成四等份,提取其中三个分割点位置的数值得到,可避免个别极大值或极小值的影响。经过对贫困用户的用电特性进行分析及多次验证后,选取方差、极值差、差分后方差、四分位数等多项特征值作为本次贫困用户识别的特征量。最后,为提升数据处理速度和分类精度,对提取出的多个特征量进行归一化处理。

2 分类模型构建

2.1 支持向量机

支持向量机是一个二元分类器,其本质是在样本中寻找一个超平面,将样本分隔开来。而该超平面的训练要求是几何间隔最大化。几何间隔是离超平面最近的样本点距超平面的欧式距离,几何间隔越大,分类误差越小[15]。

当给定一组样本数据,采用支持向量机法对数据进行分类时。首先需要提取样本的特征量,设样本中某个点到超平面的距离为d,即

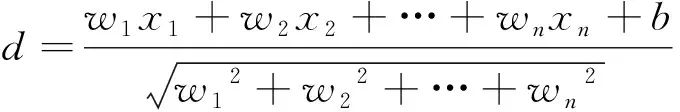
(1)

寻找超平面的要求,就是寻找几何间隔最大化,即

(2)

在很多情况下,样本是线性不可分的。此时在样本中难以找到一个合适的超平面将两者区分,需要通过核函数将样本映射到高维空间,使样本在这个空间中可分。本次采用了径向基函数(Radial basis function,RBF)核函数对贫困用户进行识别。

2.2 逻辑回归

逻辑回归是一种经典的分类方法,常用于二分类问题[16-17]。采用逻辑回归法对数据进行分类的步骤如下。

1)构建预测函数

将预测函数应用于分类时得到的结果只能为两个值,非此即彼。本文利用Logistic函数来构建预测函数,Logistic函数形式如下:

(3)

在对数据分类时,需要建立一个边界对其进行划分:

(4)

式(4)中x为多维输入变量,θ为多维输入变量对应的权值。

得到预测函数为

(5)

式(5)中的hθ(x)即为数据被判断为1的概率,那么判定为0的概率即为1-hθ(x)。

2)构建损失函数

损失函数的大小反映了分类效果。在构建损失函数时,需要利用多个样本所提供的特征量进行参数学习,通过不断的迭代修改参数使得损失函数降到最小。本次选取了拟牛顿法作为逻辑回归损失函数的优化方式。

另外,由于此次分类的样本分布比例并不平衡,所以选择根据训练样本量来计算类型权重。

2.3 神经网络

多层感知机(Multilayer Perceptron,MLP)也叫人工神经网络[18-19]。它由大量的节点彼此联接构成。不同的连接方式、权重值和激励函数所构成的神经网络输出值也有所不同。多层感知机的最底层为输入层,中间是隐藏层,最后是输出层。隐藏层输出为f(w1x+b1),其中w1为权重值,b1是偏置。本次采用tanh函数作为激活函数f(*),使用了三层神经网络,内部含有一个隐藏层,优化方式使用拟牛顿法。

3 贫困用户识别结果与分析

本文分别采用支持向量机、逻辑回归和神经网络三种模型,根据提取出的特征量对用户进行识别分类。为保证实验环境的统一,均采用python软件进行识别分析。

3.1 样本选择与模型训练

本文研究的机器学习方法都属于有监督学习,该性质决定了需要给定样本对模型进行训练。因此每次分类都按照2∶1的比例随机选取用户数据作为训练集和测试集,其中贫困用户和非贫困用户的比例与总体样本比例相同。另外为了避免特殊情况的影响,共进行20次分类,并记录分类结果数据。每次分类时都先对数据进行随机排序,分为训练集和测试集两个不重叠的部分,且每次分类时三种分类模型采用的训练集和测试集相同。

由于实际应用时识别贫困用户后需要进行实地查证,考虑到节省过程中的人力物力消耗,本文研究的主要目标是保证查找出的贫困用户的识别准确率,而不是尽量找出所有贫困用户。因此本文更注重识别模型的高精准率,而非整体高准确率和高召回率,主要针对贫困用户的分类精准率进行分析。这里贫困用户的分类精准率解释为真实贫困用户在分类得到的贫困用户中所占比例。

3.2 结果分析

分别采用三种分类模型对贫困用户进行训练及分类,训练集与测试集的比例为2∶1,得到针对贫困用户的分类精准率结果如表1和图3。

表1 分类结果精准率

精准率:分类得到的贫困用户中分类正确的用户数/分类得到的贫困用户总数;

最高精准率:20次分类中,精准率的最高值;

最低精准率:20次分类中,精准率的最低值;

平均精准率:20次分类的精准率平均值。

图3 分类结果精准率对比曲线图Figure 3 Comparison curve of classification precision

表1反映了三种分类精准率的高低分布,图3是经过20次分类得到的贫困用户分类精准率结果。由表1和图3可知支持向量机的分类精准率分布在80%～100%,平均精准率是88.20%,对该批样本中的贫困用户整体识别精准度较高。神经网络的分类精准率主要分布在50%～70%,波动幅度较大,平均精准率为56.91%。而逻辑回归的分类精准率在该类型的分类中表现较差,基本分布在40%～50%。由于该类型数据的分类存在样本分布不平衡的问题,且选择了分类精准率而不是准确率作为评价指标,因此分类结果普遍精准率不高。另一方面,针对一批相同数据进行多次分类时,支持向量机和逻辑回归表现出了较强的稳定性,每次分类得到的结果都相同,而神经网络得到的结果会产生变化,分类精准率也会随之产生变化,整体稳定性较弱。

使用混淆矩阵对结果进行可视化,混淆矩阵中的概念定义如下。

a) TP(真正):将电力用户中的贫困用户识别为贫困用户;

b) TN(真负):将电力用户中的非贫困用户识别为非贫困用户;

c) FP(假正):将电力用户中的非贫困用户识别为贫困用户;

d) FN(假负):将电力用户中的贫困识别为非贫困用户。

根据以上概念分别取三个分类模型的最佳分类效果绘制混淆矩阵如表2。

结合表2的混淆矩阵经过计算后可分别得到三个模型的精准率和召回率,如表3。

根据混淆矩阵的分析结果可知支持向量机有最高的精准率和最低的召回率,神经网络有较高的精准率,但召回率同样不高。支持向量机和神经网络识别的贫困用户整体较少,召回率较低。而逻辑回归识别的贫困用户数量较多,相应的召回率高于前两个分类模型。数据分类本身特性决定了精准率越高,相应的召回率就会越低。分类用户数的增加是召回率上升的主要原因,同时也意味着更多的非贫困用户被归类为贫困用户。逻辑回归每次分类都倾向于将测试集的三分之一分为贫困用户,原因可能是在分类模型参数设置时根据训练样本量来计算类型权重参数。通过用户的日用电量进行分析查找贫困用户进而为精准扶贫提供基础是本文研究的主要目的,从该目标要求来看,首先需要保证的是贫困用户查找的精准率。因此,支持向量机分类模型相较于逻辑回归模型和神经网络模型在电力贫困用户的识别中应用效果更好。

表2 混淆矩阵

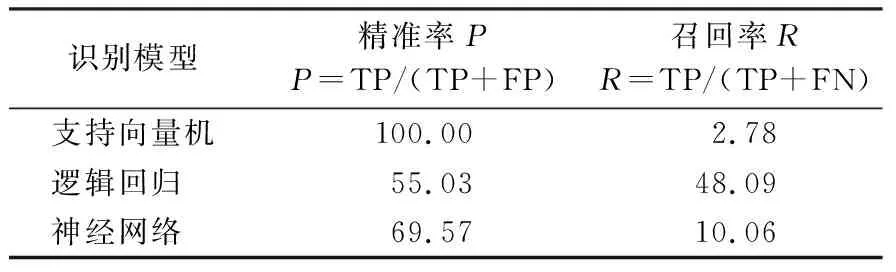
表3 识别模型的精准率和召回率

4 结 论

本文基于电力用户的日用电量信息,研究了支持向量机、逻辑回归和神经网络三种分类模型在电力贫困用户识别中的应用。由以上数据和分析结果可见,使用拟牛顿法进行迭代建立的支持向量机模型的正样本分类精准率高于另外两种方法,且分类结果也较为平稳。而逻辑回归存在将更多的用户划为贫困用户的现象,导致了正样本分类精准率较低。神经网络识别在本次的应用结果精准率介于以上二者之间,但稳定性有所欠缺。三种方法均具有一定的局限性,但由于高精准率是本次针对电力贫困用户进行识别的主要目标。因此,相较之下,支持向量机法更加适用于电力贫困用户识别的实际应用。

同时,本文的研究仍存在一些问题。支持向量机法应用于电力贫困用户识别方面时的召回率不高,后期研究需要在保证高精准率的同时提升召回率。该问题也可能与数据前期处理有关系,故对于数据的前期处理可进行更加深入的研究。针对神经网络识别模型则需要改进它的分类稳定性,同时可以考虑采用多种分类方法相结合的方式对分类精准率进行提升。对于逻辑回归分类模型则可考虑对样本权重参数进行改进设置,也可通过改进惩罚函数等以提升它的分类精准率。另外,对电力用户的不平衡分类进行进一步探讨也可成为下一步的研究方向。