巧用“一线三等角”模型解题

王友峰

对于初中几何的学习，我们除了需要掌握课本中的定义、定理等基本知识外，还要对一些基本模型进行积累，下面给同学们介绍一个基本模型：“一线三等角”.

一、引例

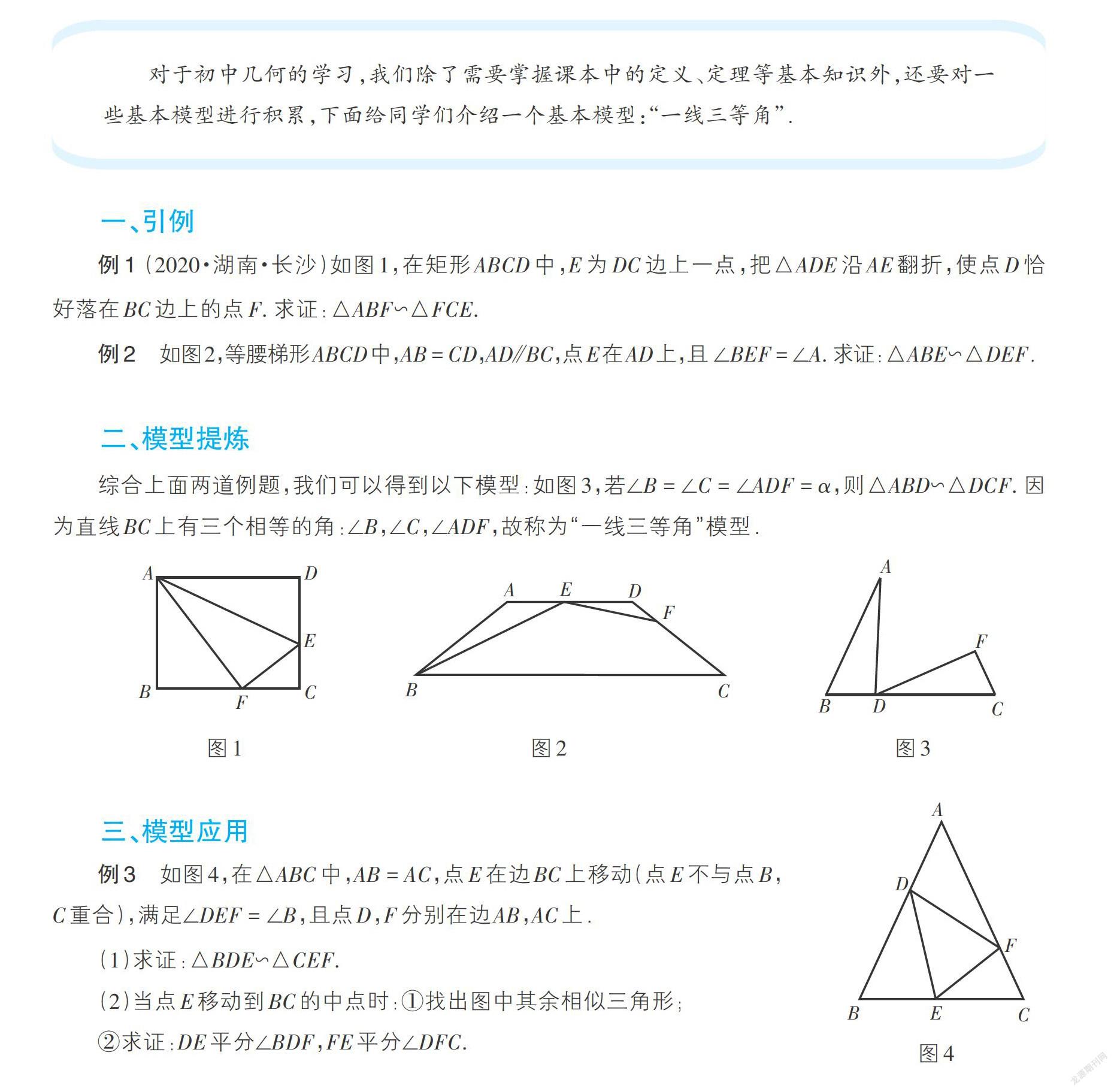
例1 （2020·湖南·长沙）如图1，在矩形ABCD中，E为DC边上一点，把△ADE沿AE翻折，使点D恰好落在BC边上的点F. 求证：△ABF∽△FCE.

例2 如图2，等腰梯形ABCD中，AB = CD，AD[⫽]BC，点E在AD上，且 ∠BEF = ∠A. 求证：△ABE∽△DEF.

二、模型提炼

综合上面两道例题，我们可以得到以下模型：如图3，若∠B = ∠C = ∠ADF = α，则△ABD∽△DCF. 因为直线BC上有三个相等的角：∠B，∠C，∠ADF，故称为“一线三等角”模型.

[A][D][E][C][F][B] [D][E][A][B][C] [F][A] [F][C][D][B]

      图1             图2     图3

三、模型应用

例3 如图4，在△ABC中，AB = AC，点E在边BC上移动（点E不与点B，C重合），满足∠DEF = ∠B，且点D，F分别在边AB，AC上.

（1）求证：△BDE∽△CEF.

（2）当点E移动到BC的中点时：①找出图中其余相似三角形;

②求证：DE平分∠BDF，FE平分∠DFC.

解析：（1）∵AB = AC，∴∠B = ∠C，∵∠DEF = ∠B，∴∠B = ∠C = ∠DEF，

根据“一线三等角”模型，易证△BDE∽△CEF.

（2）①∵△BDE∽△CEF，∴[ BDCE] = [  DEEF]. ∵E是BC的中点，∴BE = CE，

∴[BDBE] = [  DEEF]，∴[BDDE] = [  BEEF]. ∵∠DEF = ∠B，∴△BDE∽△EDF.

同理，△CEF∽△EDF.

②∵△BDE∽△EDF，∴∠BDE = ∠EDF，∴DE平分∠BDF.

同理，由△CEF∽△EDF，得FE平分∠DFC.

点评：问题（1）具备了“一线三等角”要素即可证明三角形相似，本题中若有ED = EF，则可得这两个相似三角形全等.

例4 （2020·湖北·鄂州）如图5，点A是双曲线y = [1x]（x<0）上一动点，连接OA，作OB⊥OA，且使OB = 3OA，当点A在双曲线y = [1x]上运动时，点B在双曲线y = [kx]上移动，则k的值为     .

解析：如图5，分别过点A，B作AC⊥x轴于点C，BD⊥x轴于点D，由“一线三等角”模型，易得△ACO∽△ODB，∴S△ACO∶S△ODB = [OAOB2] = [19]. ∵S△ACO = [12]，S△ODB = [|k|2]，∴|k| = 9，k = -9.

点评：过点A，B分别作x轴的垂线构造出两个直角，这样就具备“一线三等角”条件了.

四、能力提升

1. （2020·湖北·十堰）如图6，菱形ABCD的顶点分别在反比例函数y = [k1x] 和y = [k2x]的图象上，若∠BAD = 120°，则[k1k2]等于（ ）.

A. [13] B. 3

C. [3] D. [33]

提示：连接CO，DO，則CO⊥DO，且∠DCO = 60°，DO = [3]CO，再过点C，D作x轴的垂线，仿照例4构造“一线三等角”模型，可得选项B.

2. 如图7，直线AB与坐标轴交于点A（3，0），B（0，6）. 直线BC交x轴于点C，点C在点A的右侧，且满足tan∠ABC = [13]，求点C的坐标.

提示：过点A作AD⊥BC，垂足为点D，过点D作DE⊥x轴于点E，作BF⊥ED于点F，构造 “一线三等角”模型，可得点C的坐标为（6，0）.

（作者单位：江苏省苏州工业园区青剑湖学校）