数控机床进给系统运动精度与能耗控制研究*
2021-11-27朱若岭
周 微,朱若岭,张 昊
(1.常州机电职业技术学院 机械工程学院,江苏 常州 213164;2.河南交通职业技术学院 汽车学院,河南 郑州 450000;3.东南大学 仪器科学与工程学院,江苏 南京 210096)
0 引 言
由于能源短缺等的原因,节能降耗成为了目前制造业领域迫切需要解决的问题[1,2]。世界范围内,制造业领域约三分之一的能源消耗于数控机床的加工过程,而其中进给系统是其产生能耗的主要部件[3]。因此,控制进给系统的能耗对于降低数控机床加工过程总能耗具重要的意义[4,5]。
目前,世界各国在数控机床加工过程中能耗控制方面的研究均取得了一定进展。在国内,曹昆仑等人[6]提出了一种基于载荷损耗系数的能耗数学模型,分析了机床切削负载率、实载率和机床效率、能量利用率之间的关系。李聪波等人[7-9]基于磨损机理,提出了一种考虑刀具磨损的数控车削批量加工工艺参数节能优化方法。何吉祥等人[10]通过构建结构节能优化模型,提出了降低数控车床主轴单元能耗的方法。张朝阳等人[11]基于迁移学习方法,研究了数控机床等待过程的节能控制策略。陈世平等人[12]利用BP-Adaboost方法,提出了基于数据驱动的数控机床切削过程能耗预测模型。徐秀玲等人[13]以SIEMENS840D sl数控系统为例,提出了一种机床待命、系统待命和关机3种节能控制方案,并将其应用于龙门式数控铣床中。李聪波等人[14]基于元动作技术,提出了一种数控车削能耗预测的数据驱动方法。
目前,国内在数控机床能耗分析、预测及控制领域的研究多集中于切削过程,而对进给系统运动、控制过程中的能耗研究较为缺乏。
国外方面,SATO R等人[15]针对五轴加工中心,研究了工件装夹位置与进给系统能耗间的关系。WANG Y等人[16]研究了固定时间间隔内,进给系统的实时能耗最优化轨迹生成问题。FARRAGE A等人[17]提出了基于傅里叶级数的非线性摩擦补偿模型,以减少进给系统中未知摩擦力所造成的能耗。MOHAMMAD A E K等人[18]基于非线性滑模轮廓控制,对数控机床进给系统的降耗进行了研究。
实际上,进给系统的能耗不仅取决于各轴的运动轨迹,还取决于其控制效果。因此,在相同的运动轨迹下,由于控制器增益的影响,进给系统能耗会发生变化。然而,前述研究均利用的是固定的控制增益,因此无论其跟踪性能如何,所采用的控制方法都消耗相同的能量。一般而言,虽然使用较高的控制增益会提高其运动精度,但也会导致其能耗增加,故而必须同时考虑控制器的跟踪性能及能耗,才能满足生产效率和节能降耗两方面的要求[19]。FARRAGE A等人[20]提出了一种自适应滑模轮廓控制方法,研究了双轴进给系统的运动精度及能耗控制问题。
然而,上述方法仅能通过滑模控制的到达阶段降低能耗,对滑动阶段的能耗未加以考虑。
综上所述,本研究针对数控机床进给系统位置精度及能耗控制两方面的需求,基于SMC原理,提出一种具有非线性滑模面的ASMC方法,通过设计全新的自适应趋近律,对到达和滑动阶段的控制增益进行更新,提供控制增益的最小容许值,在保证位置跟踪精度的基础上降低能耗;最后通过实验进行对比研究,以验证该方法在位置跟踪精度及能耗控制两方面的优势。
1 进给系统动力学模型
笔者所采用的实验进给系统如图1所示。

图1 实验进给系统
该系统包含2台交流伺服电机、2个分辨率为76.29 nm(经角度-位移换算后)的旋转编码器(用于测量工作台位置),采样时间为0.2 ms。双轴滚珠丝杠均为C1级高精度定位型。
为获得准确的系统模型,笔者采用扰动观测器(DOB)对控制参数进行估计;进给系统两轴采用相同的辨识方案。
进给系统的动力学模型为:
(1)
式中:qi,mi—X、Y工作台的位置和质量;gi,fi—摩擦力和驱动力。
PID与DOB参数如表1所示。
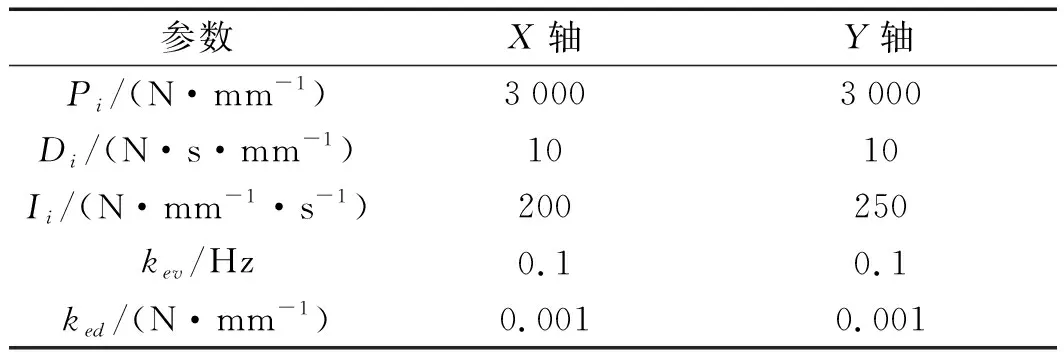
表1 PID与DOB参数
用于参数辨识的驱动力fi为:
(2)
式中:Pi,Di,Ii—比例、微分和积分控制增益;ei—跟踪误差,定义为期望位置ri和实际位置qi之间的差值。
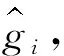
(3)

利用表1所示的PID和DOB参数,结合观测数据得到的摩擦模型为:
(4)
式中:fci,ci—库仑摩擦系数和粘性摩擦系数。
实验进给系统的关键参数如表2所示。
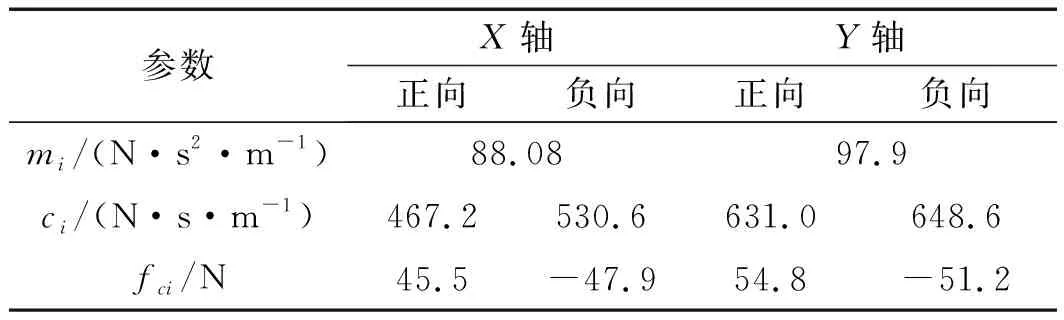
表2 实验进给系统关键参数
摩擦力模型参数辨识结果如图2所示。

图2 摩擦力模型参数辨识结果
由图2可知,所辨识出的参数与实际系统参数较为符合。因此,摩擦特性可只用库仑系数和黏性系数来描述。进给系统机械动力学可以用二阶解耦系统模型表示,即:

(5)
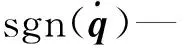
2 ASMC方法及其稳定性分析
2.1 SMC方法概述
SMC方法所采用的非线性滑模面可表示为:
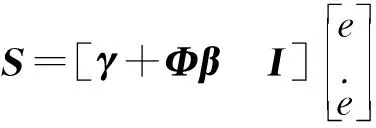
(6)
式中:S—二维滑模面矢量;γ—正定矩阵,用于提供快速响应,并使占优极点满足Lyapunov方程:βγT+γβ=P(其中:P—正定矩阵;β—用于调整阻尼比的正定对角阵;Φ—以Φi为元素的对角阵,当输出从初始值变为期望值时,利用该矩阵将阻尼比从较低值调整为较高值)。
由于Φi没有唯一的公式,此处采用如下形式[22]来表示:
Φi=ηi[exp(-ei)+exp(ei)],i=x,y
(7)
式中:ηi—用于调整Φi大小的正值。
对于理想滑模面,式(6)可变为:
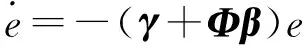
(8)
此时,通过适当调整(γ+Φβ)的值,跟踪误差将收敛到零[23],驱动系统状态趋于S=0。此处所采用的趋近律可表示为:
(9)
式中:k—2×2增益矩阵;sgn(S)—滑模面符号矩阵;h—包含元素hi的2×2矩阵。
且有:
hi≥di
(10)
2.2 ASMC方法原理
虽然式(9)所示控制律具有良好的控制性能,但由于其增益k是固定的,在整个运行时间内趋近律的能耗将维持不变。此外,虽然较高的增益值通常会降低控制误差,但也会导致能耗增加。
为解决上述问题,可采用自适应趋近律。典型的自适应滑模趋近律采用如下增益[24,25]:
(11)

然而,尽管采用式(11)所示增益的自适应趋近律可提高进给系统的运动精度,但是在达到期望的控制精度时,无法将增益更新至较低的数值。因此,上述自适应趋近律只能在到达阶段降低能耗,而不能在滑动阶段降低能耗。
为克服上述缺点,文献[26]提出了一种自适应滑模趋近律,其增益在到达和滑动阶段均可改变,即:
(12)
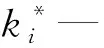

为提供更快的自适应速率,减少到达和滑动阶段的跟踪误差,文献[27]735提出了基于开关增益的自适应滑模趋近律:
(13)
然而,尽管采用增益(13)的自适应趋近律可降低能耗,但会因跟踪误差增加从而使控制性能降低。此外,由于期望边界层周围的误差幅度变化,控制信号将出现较大的抖振。
为了解决上述各自适应控制律的缺陷,笔者提出了一种新的ASMC方法,所采用的控制增益可根据跟踪误差的平方值,以更快的自适应速率自动更新,即:
(14)
当趋近律进入到达阶段时,将激活式(14)中的第一个条件,以提供更快的适应速率,降低控制信号作用时间。当增益(14)的第2个条件激活时,控制增益略有下降,但仍能在降低能耗的同时保持控制方法的跟踪性能。
笔者所采用的自适应滑模趋近律表示为:
(15)
2.3 稳定性分析
2.3.1 滑模面稳定性分析
Lyapunov候选函数为:
V1=eTβe
(16)
根据式(8),式(16)的时间导数可表示为:
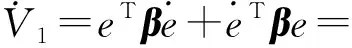
(17)
式中:P,β—正定矩阵。
其中:Z=βe。由于V1≤0,保证了受控系统在理想滑模面上的稳定性。
2.3.2 控制系统稳定性分析
Lyapunov候选函数为[28]:
(18)
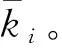
式(18)的一阶时间导数为:
(19)
(20)
根据式(5),系统误差动力学模型可表示为:
(21)
(22)
式(14)中的两个自适应律条件为:
(1)当|si|≥δi时,式(22)表示为:
(23)

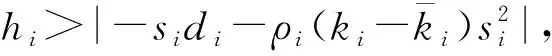
为使滑模面收敛到零,依据Barbalat引理[29]有:
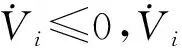
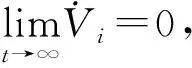
(24)
式中:Δi—平滑项。
3 实验及结果分析
为了验证该控制律的有效性,笔者利用图1所示的实验装置来进行验证。系统进给速度为25 mm/s的,其圆周运动轨迹为:
(25)
通过试错法得到了其控制参数,如表3所示。

表3 控制参数
各自适应控制方法实施流程如图3所示。

图3 各自适应控制方法实施流程
笔者采用相同动力学模型和控制技术,利用表3所示的相同控制参数,对该ASMC方法的跟踪性能和能耗进行验证,并将其与采用式(11~13)增益的自适应趋近律进行比较。
在相同控制参数条件下,基于控制律式(11~14)的控制信号如图4所示。
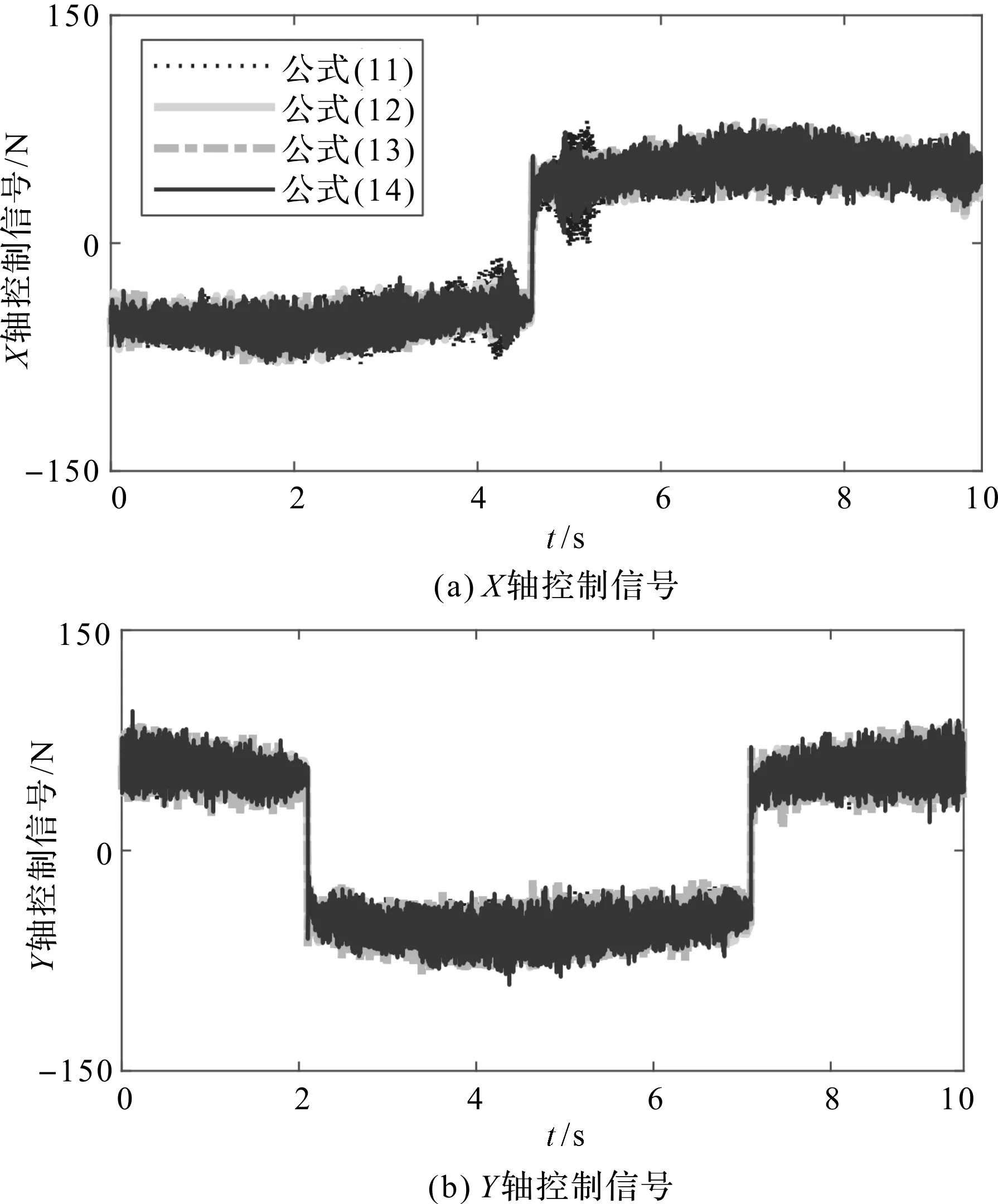
图4 相同控制参数条件下基于控制律(11~14)的控制信号
在相同控制参数条件下,基于趋近律(11~14)的平均定位误差如图5所示。
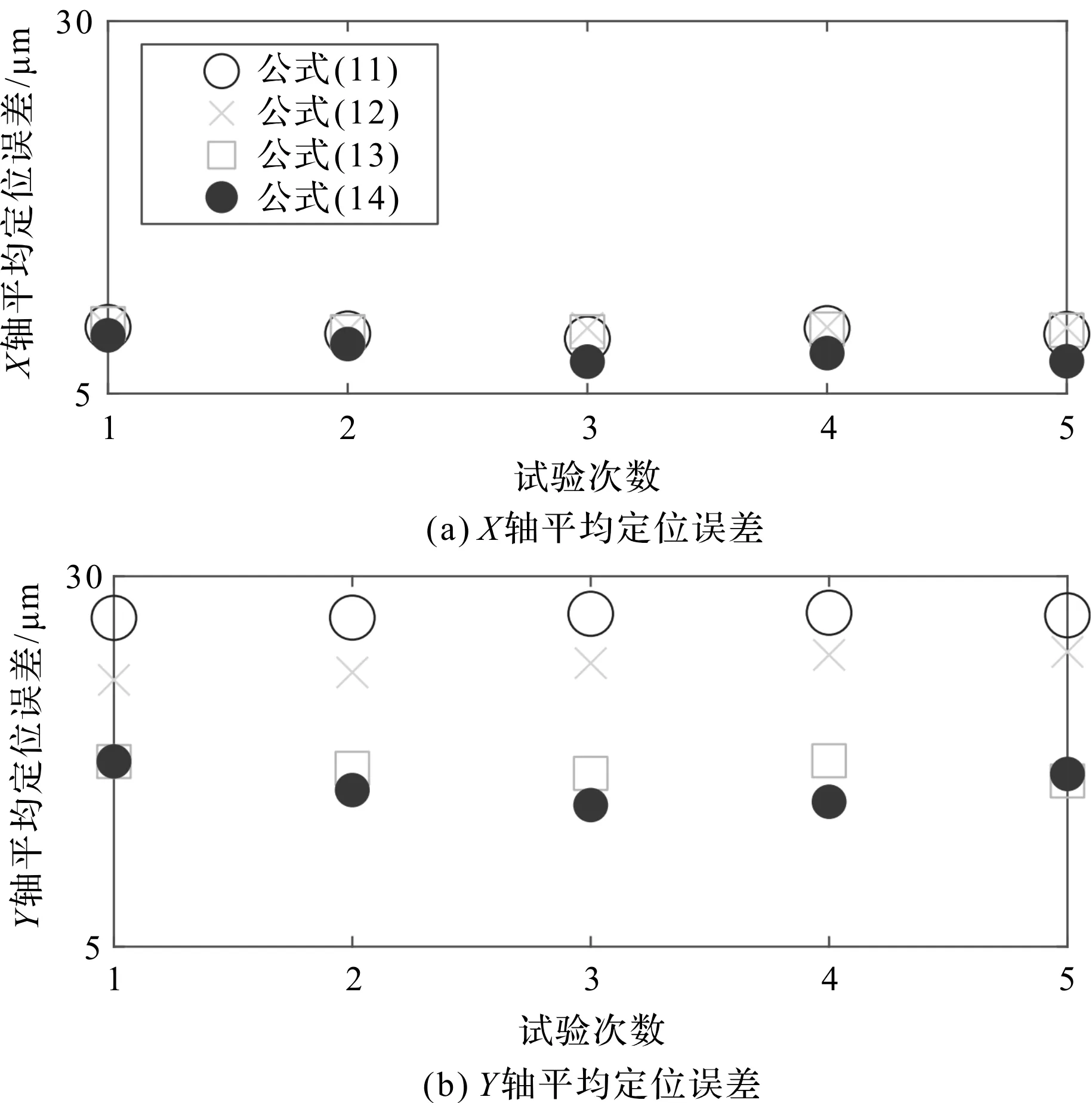
图5 相同控制参数条件下基于趋近律(11~14)的平均定位误差
在相同控制参数条件下,基于控制律(11~14)的最大定位误差如图6所示。
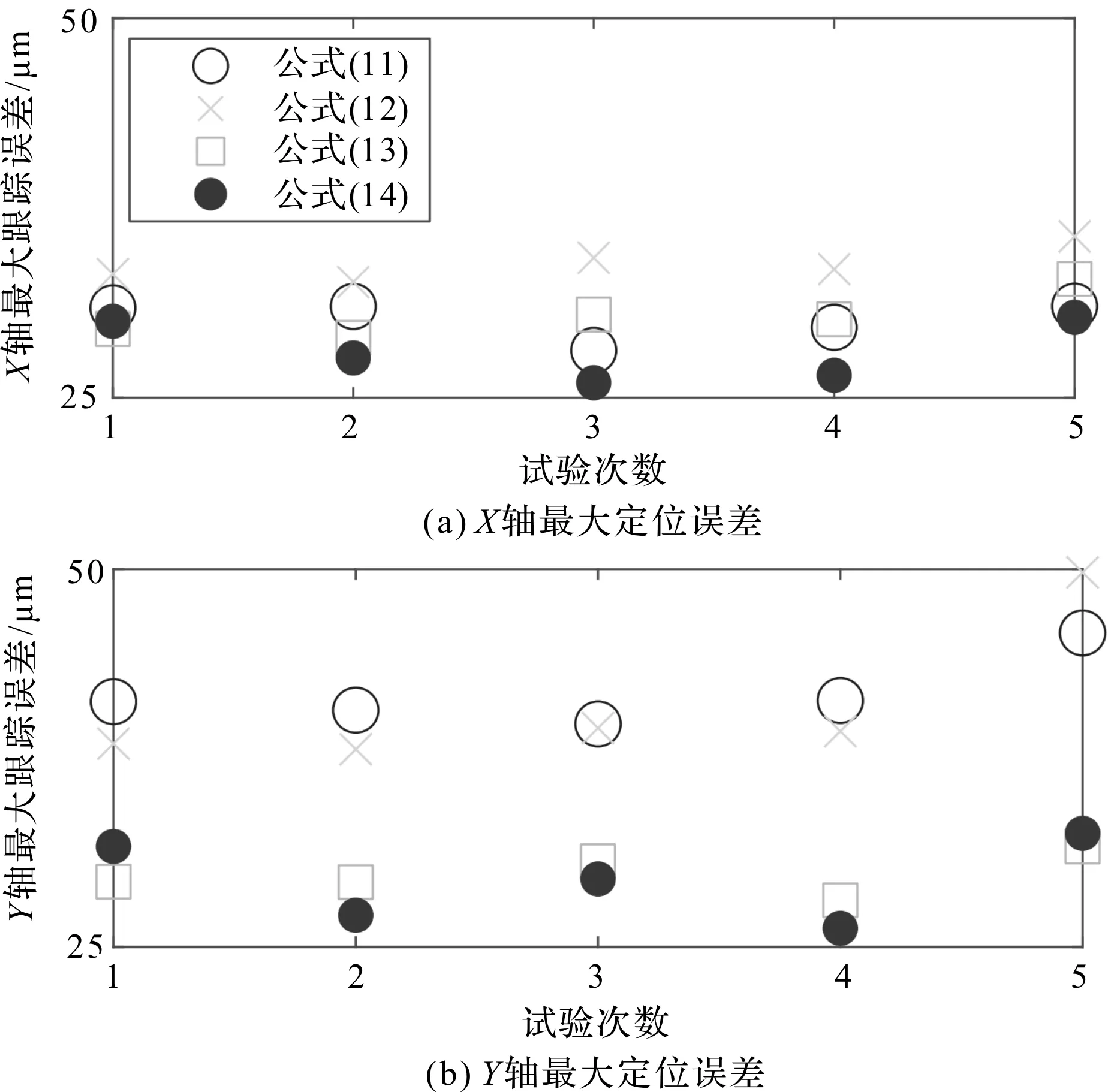
图6 相同控制参数条件下基于控制律(11~14)的最大定位误差
在相同控制参数下,不同控制律的能耗如表4所示。
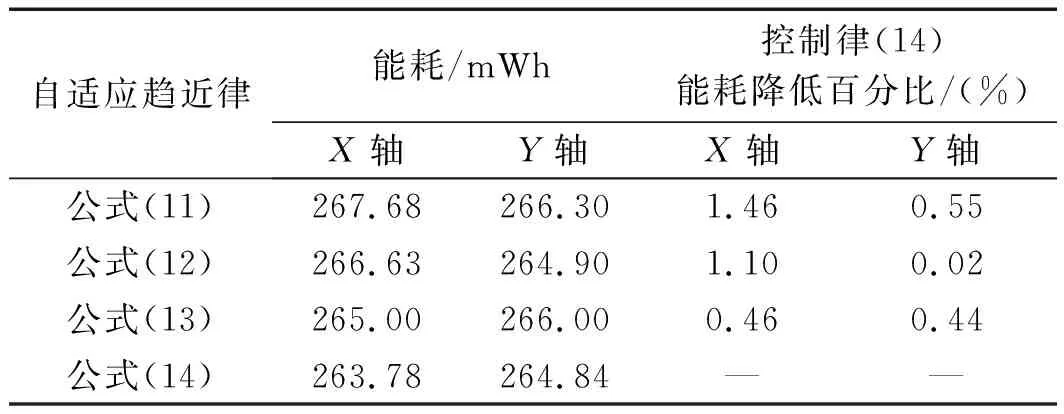
表4 相同控制参数下不同控制律的能耗
在相同控制参数下,不同控制律平均及最大定位误差如表5所示。
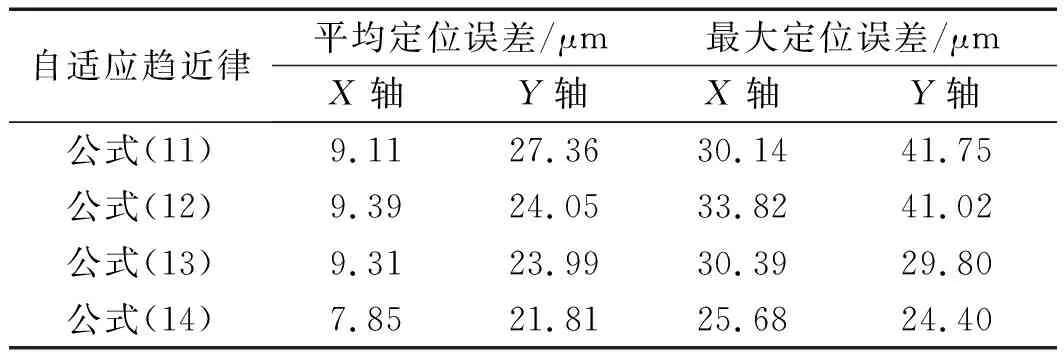
表5 相同控制参数下不同控制律平均及最大定位误差
实验中,控制过程的能耗采用功率计(HIOKI 3390AC/DC)进行测量。由表5可知:与采用增益(11~13)的自适应趋近律相比,所提出的ASMC方法可在提高跟踪精度的同时降低控制能耗。
同时,在跟踪性能相近的条件下,笔者比较了前述各自适应趋近律的能耗。为获得与ASMC方法近似的跟踪误差,增益(11~13)中的适应率值ρ分别设置为[10 30]T、[30 60]T和[7 5]T,并将式(6)中γ分别设置为[50 80]T、[50 70]T和[50 60]T,以调整控制器阻尼比。
在相同定位精度下,不同控制律的平均及最大跟踪误差如表6所示。
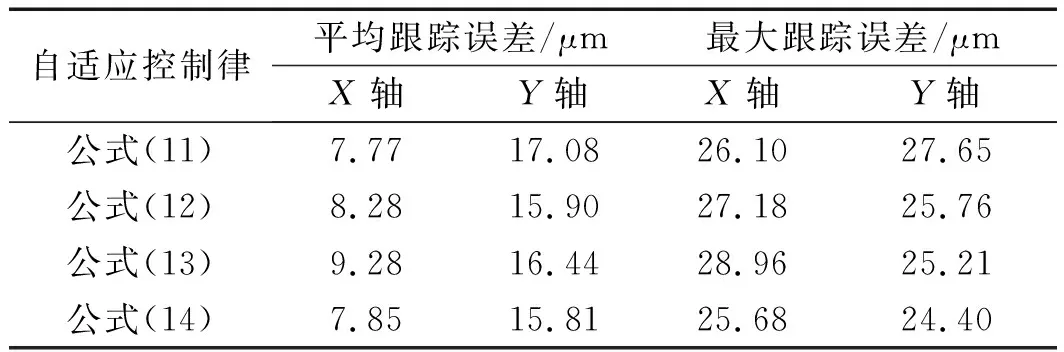
表6 相同定位精度下不同控制律平均及最大跟踪误差
由表6可以看出:各方法的控制性能相近;式(11)所示的控制增益在达到其上限值后保持常数,因此该方法的能耗与其跟踪精度无关;控制增益(12)可在其到达和滑动阶段进行变化,然而其适应速率较低;采用控制增益(13)的自适应趋近律时,由于其控制信号连续性差,所产生的跟踪误差较大。
在相同控制性能条件下,基于控制律(11~14)的控制信号输入如图7所示。

图7 相同控制性能条件下基于控制律(11~14)的控制信号输入
在相同控制性能条件下,控制律(11~14)的能耗如图8所示。

由图7及图8可以看出:各方法的控制信号(与能量消耗直接相关)差异较大;与采用式(11~13)所示的控制增益的自适应方法相比,采用ASMC方法可使X轴和Y轴能耗分别降低1.74%和0.79%、0.99%和0.26%、0.96%和0.92%。
此外,控制输入信号的标准差是评价控制方法产生抖振现象强弱的指标,即:
(26)
式中:ui—控制信号的平均值;fij—第j个采样时刻的控制信号幅值,j=1,2,…,J;J—采样次数。
在相同控制性能条件下,基于控制律(11~14)的输入信号标准差如图9所示。
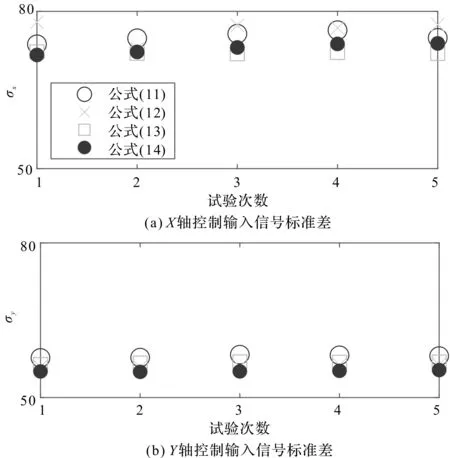
图9 相同控制性能条件下基于控制律(11~14)的输入信号标准差
由图9可以看出:与采用式(11~13)所示的控制增益的自适应方法相比,ASMC方法控制输入信号标准差(X轴和Y轴)分别降低了2.90%和4.97%、4.63%和1.76%、-1.22%和2.88%。
由此可见,笔者提出的控制方法在保证相同控制性能的前提下,可有效降低控制能耗及系统抖振。
4 结束语
基于进给系统动力学模型及SMC理论,笔者通过设计全新的自适应控制增益,提出了相应的非线性ASMC方法;该方法提供了更快的自适应速率,可在保证位置跟踪精度的基础上降低控制能耗;利用实验对该方法进行了验证。
研究结果表明:
(1)与其他自适应控制方案相比,所提控制方法在控制参数相同的条件下,可使进给系统定位精度更高,且X、Y轴的平均定位误差最多可分别降低16.4%及20.3%;
(2)与其他自适应控制方案相比,在控制性能相同的条件下,所提控制方法产生的能耗最少,X轴和Y轴的控制能耗最大可分别降低1.74%及0.96%;
(3)与其他自适应控制方案相比,所提控制方法能够更为有效地抑制系统的抖振。
在后续的研究中,笔者将研究控制输入信号的幅值对上述自适应方法的影响;同时采用最优化理论选取其最佳增益值,从而获得更高的位置跟踪进度,也使控制能耗可得到进一步的降低。
