基于时延欠阻尼随机共振的轴承微弱故障诊断*

2021-11-27李志星王光进鲍慧茹

机电工程 2021年11期

关键词：势阱共振稳态

李志星,王光进,鲍慧茹

(1.北京建筑大学城市轨道交通车辆服役性能保障北京市重点实验室,北京 102612;2.内蒙古科技大学机械工程学院,内蒙古包头 014010;3.包头职业技术学院,内蒙古包头 014030)

0 引言

随着装备制造业的快速发展,旋转机械在工程应用领域发挥了越来越重要的作用。而轴承等旋转部件的故障会影响设备的正常运行,导致机器损毁、人员伤亡。因此,对旋转机械进行故障诊断极有必要[1-3]。

在机械早期微弱故障特征提取中,传统的信号处理方法有多种,如小波分析法[4]、包络解调分析法[5]和经验模态分解法[6]等。在微弱故障特征提取中,因为在绝大多数情况下,噪声所起的是消极作用,所以传统的方法主要针对的是抑制或滤除其噪声。

在针对滚动轴承故障响应不良的问题方面,MENG Ling-jie等人[7]提出了一种基于二代小波去噪和形态学滤波的方法,并将其用于提取缺陷轴承的缺陷信息。为了更好地检测轴承的早期故障,PATEL A等人[8]提出了一种基于经验模态分解的方法,将其用于解决轴承原始振动信号提取困难的问题。

但是,由于轴承早期的故障信号往往很微弱,在滤除噪声的过程中,也易滤去其中的有用信号,削弱故障特征信号,影响信号的检测效果。

针对以上方法存在的问题,笔者拟采用噪声增强有用信号强度的方法,即随机共振方法[9],来提取微弱的故障特征。随机共振方法最早是研究人员在研究地球古气象冰川问题时提出的,现在该方法已被广泛应用于各个研究领域[10-13]。为了更深入地研究随机共振,ZHANG Gang等人[14]提出了一种改进势函数随机共振的方法,该方法可用于经典随机共振饱和性和参数调节问题的研究。

在研究强噪声下的故障诊断问题时,为了更好地增强微弱故障的特性,李志星[15]在势模型结构和参数方面对该方法进行了改进。为了进一步提高随机共振的效果,一些研究者又提出了基于三稳态电位的随机共振方法[16,17]。但上述研究并未考虑时延和欠阻尼对随机共振的影响。

近年来,一些学者对具有时延的随机共振进行了研究。韩松久[18]采用时延的方法,并结合不同的势模型来对机械故障进行了诊断。对于系统存在的非线性,ZHONG Su-chuan等人[19]分析了具有分数阶时滞和多项式噪声振荡器中的输出幅度增益,并对这一类的广义随机共振进行了论述。SUN Xiao-juan和LIU Zhao-fan[20]研究了时延和噪声这两个因素对小世界神经元网络检测亚阈值信号能力的综合影响。

此外,还有一些学者提出了一种欠阻尼随机共振的方法,来增强微弱信号的强度。XU Peng-fei等人[21]研究了欠阻尼三阱势能系统中的随机共振,并据此证实,适当的三阱势函数和阻尼系数可以改善系统对外部周期性激励的响应。CHI Kuo等人[22]提出了一种基于神经网络和布谷鸟搜索算法的自适应欠阻尼随机共振方法,并将其借此对轴承的微弱故障进行了检测。LU Si-liang等人[23]提出了一种欠阻尼阶跃变阶随机共振方法,并采用适当的阻尼因子和计算步骤,使系统成分能够相互匹配,进一步提高了输出信噪比。

上述学者所提出的基于时延或欠阻尼的方法,还无法检测更为复杂的故障信号,因此,笔者提出一种基于时延欠阻尼三稳态的随机共振方法,并将其应用于轴承的微弱故障诊断中;将其与经典时延随机共振方法、经典欠阻尼随机共振方法进行相比,以证明该方法在微弱故障特征提取、信号输出效果方面更优秀。

1 时延欠阻尼三稳态随机共振方法

1.1 时延欠阻尼三稳态随机共振模型

在随机共振发生的3个条件中,噪声和周期力的大小始终保持不变。为了适应复杂的噪声环境,使粒子在势阱之间的运动状态更加平稳,通过调节势函数的参数,即可实现输入信号的放大。

为了进一步优化经典模型的结构,笔者提出了一种新的三稳态势模型[24]:

U(x)=x2[a+(bx2-c)2]

(1)

式中:a,b,c—势函数的3个系统参数,其中,a>0,b>0和c>0。

不同参数的势模型结构如图1所示。

图1(a)中,当b=10,c=6时,参数a的值影响着势阱的宽度、势壁的陡峭度和势阱的深度;参数a的增大,使得壁陡度和中间势阱的深度增大,而势宽度和两侧势阱的深度变小,因此,粒子难以从中间势阱运动到两侧势阱;

在图1(b)中,势阱的宽度和两侧势阱的高度由参数b决定,其中,a=0.5,c=7;b越大,势阱越浅,粒子跃迁就越容易,随机共振才越好发生;

在图1(c)中,当a=0.1,b=1时,参数c调节着势阱的宽度和势阱的深度;参数c变大,势形状就变大,导致粒子很难在相邻的势阱之间发生跃迁,并且其所需的能量也会越大。

经典随机共振模型的输出由前一个输出决定,通过把长记忆项加入到随机共振的负反馈环节,使得系统的输出由前面的多个输出决定,从而使微弱信号得以增强。

在经典随机共振方程中引入时延反馈项[25],即有:

(2)

式中:β—反馈强度;τ—时延长度;A—周期信号幅值;D—噪声强度;ξ(t)—高斯白噪声,符合〈ξ(t)〉=0及E[ξ(t)ξ(t+τ)]=2Dδ(t-τ)。

将式(1)代入式(2),可得到新的时延三稳态方程:

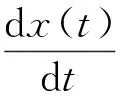
(3)

式(2)是一个非马尔科夫过程,把概率密度方法简化为马尔科夫过程,其近似时延Fokker-Planck方程如下[26]:

(4)

式中:he—条件平均漂移率。

条件平均漂移率he表达式为:

(5)

式中:m,n—积分边界±∞;P(xτ,t-τ|x,t)—零阶近似马尔可夫链转移概率密度。

其中：xτ=x(t-τ);h(x,xτ)=6b2x5-8bcx3+2(a+c2)x+βxτ+Acos(Ωt)。

P(xτ,t-τ|x,t)的公式为[27]:

(6)

其中:h(x)=6b2x5-8bcx3+2(a+c2)x+βx+Acos(Ωt)。

将式(6)代入式(5)可得:

he=(1+βτ)[6b2x5-8bcx3+2(a+c2)x]+
β(1+βτ)x+(1+βτ)Acos(Ωt)

(7)

进一步地,可以获得等效的Langevin方程:

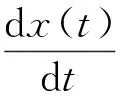
(8)

将其与式(3)对比可知,一耦合项被添入系统。

在不考虑周期信号和高斯噪声的情况下,式(8)的等效时延三稳态势阱可推导为:

(9)

等效时延势阱的图像如图2所示。

图2 不同参数对等效时延三稳态势阱的影响

图2(a)中,参数a=2,b=0.5,c=2.5,τ=0;在反馈强度β取值较小,而其余参数为定值时,两侧势阱的深度较大,粒子的过渡困难,并且粒子跳过势垒进入中间势阱需要的噪声能量更多;随着反馈强度β的值增加,两侧势阱的深度变小,在需要极少能量下,粒子更容易从两侧的势阱跃迁到中间势阱;

图2(b)中,参数a=2,b=0.5,c=2.5,β=3;当时延长度τ的值变大时,中间势阱的势垒变小,两侧势阱的深度减小,粒子更容易实现在阱间的过渡。

图2中,参数β和τ的变化均引起了等效势阱结构的改变;并且随着势能的不断增加,减少了粒子从一势阱越到另一势阱的能量消耗,增加了系统的输出,所以该系统可以更好地用来检测微弱信号。

将式(9)引入欠阻尼二阶随机共振模型,即:

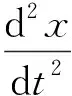
(10)

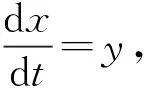
(11)

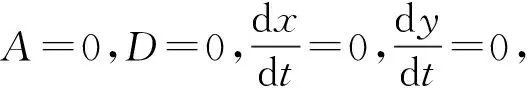
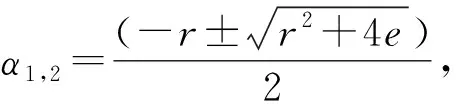
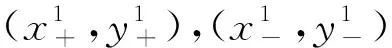
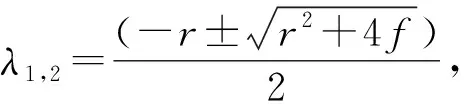
粒子运动的概率密度函数P(x,y,t)可由Fokker-Planck方程推出:

(12)

其中:h(x)=(1+βτ)(6b2x5-8bcx3+2ax+2c2x+βx)-ry+Acos(Ωt)。

根据绝热近似理论,可得到分布函数为:

(13)

广义势阱函数u(x,y,t)的表达式为:

(14)

另外,粒子在3个势阱间的概率转移率表示为:

(15)

将式(14)代入式(15)可得:

(16)

根据泰勒方程,将式(16)进行展开,可得到:

(17)

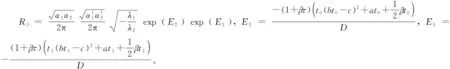
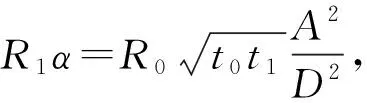
(18)

(19)

(20)

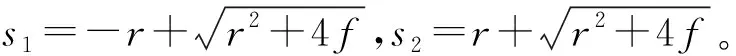
SNR的变化图像中,SNR与β的变化关系如图3所示。

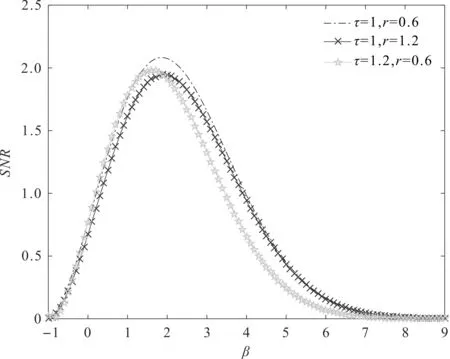
图3 SNR与β的变化关系注:a=1,b=0.6,c=1.21,Ω=0.5,A=1,D=2.25

图3反映了反馈强度β和SNR的变化关系,即随着反馈强度β的增加,SNR逐渐增加到最大值,之后开始下降;并且在时延长度τ和阻尼因子r的分别作用下,输出SNR曲线向下移动,降低了信噪比在某一时刻所能达到的最大值。

SNR与τ的变化关系如图4所示。

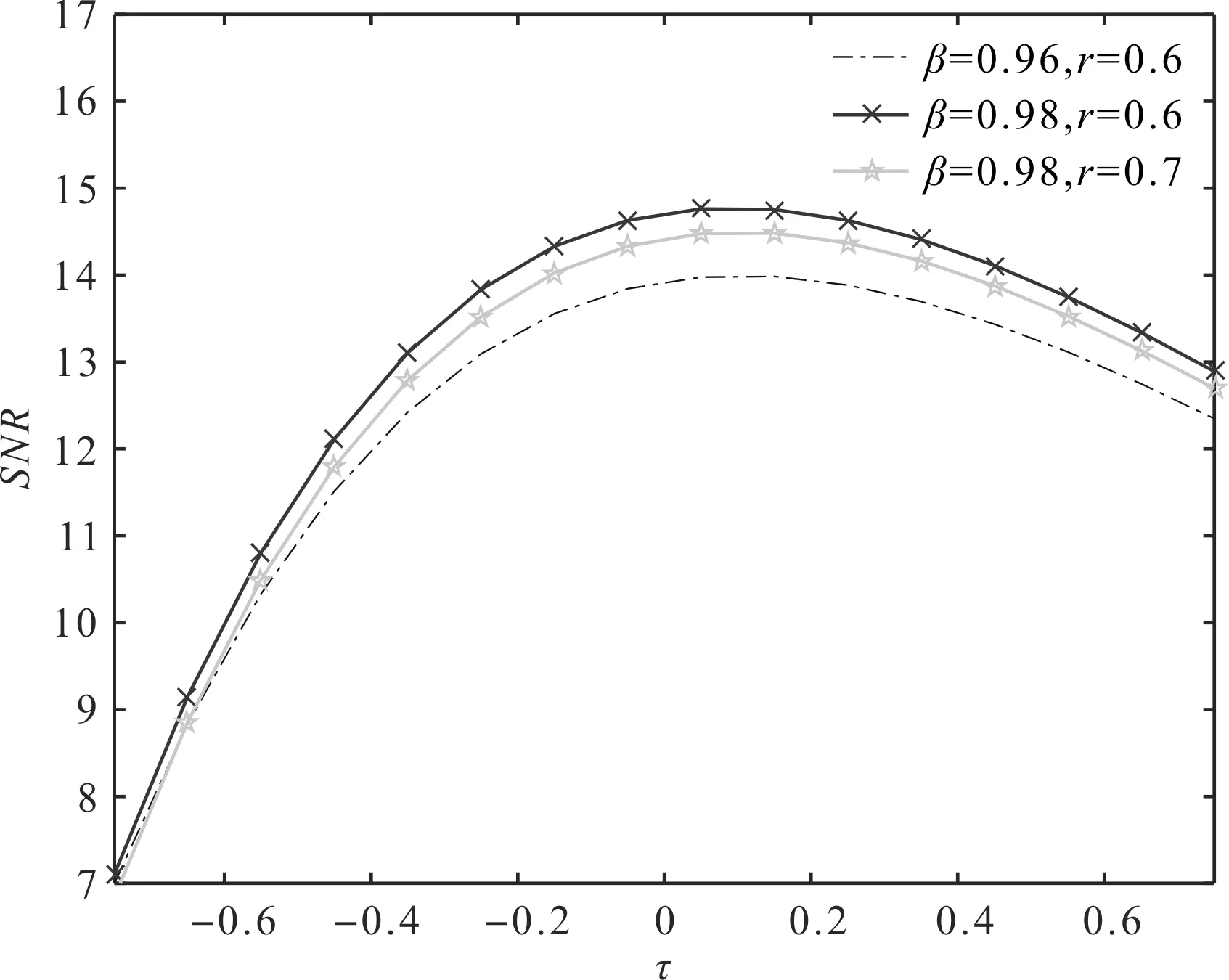
图4 SNR与τ的变化关系注:a=0.35,b=1,c=1.5,Ω=0.5,A=1,D=2.25

图4反映了时延长度τ和SNR的变化关系(该关系和图3中的变化趋势类似),但是在相同时延长度下,反馈强度β的值越大,SNR越大;而阻尼因子r的值越大,SNR的输出值则变小。

从图3和图4中可以看出:反馈强度β、时延长度τ和阻尼因子r都与SNR的输出密切相关;SNR的值越大,反映了粒子在势阱间的周期运动越稳定,体现了该系统的随机共振效应越好。

因此,通过调节上述各个参数就可以得到时延欠阻尼三稳态随机共振的最佳输出。

1.2 时延欠阻尼三稳态随机共振的信号检测方法

在上一小节,笔者分析了时延欠阻尼随机共振模型和输出信噪比。但是,要利用随机模型处理工程信号,需要解决在小参数范围下随机共振理论的限制。因此,笔者利用SNR作为该系统参数的衡量标准,借助参数的变化得到SNR的大小,进而判定时延欠阻尼三稳态随机共振方法的输出能力。

其中,SNR的定义为:

(21)

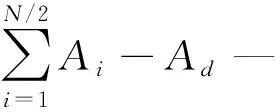
这里SNR的取值可以标定信号与噪声的比例。

为了得到最优的输出信号,笔者提出的时延欠阻尼随机共振的信号处理过程,如图5所示。

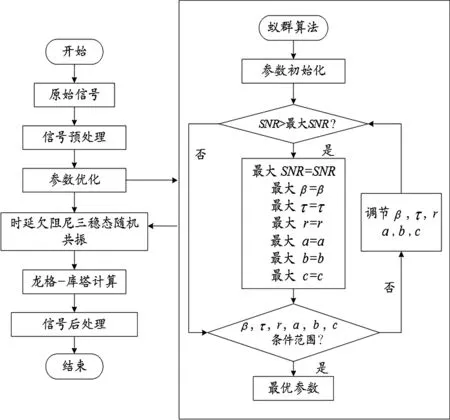
图5 时延欠阻尼随机共振的微弱信号检测方法

该处理过程的具体步骤为:

(1)信号预处理。通过信号解调获取包络信号,对包络信号进行移频重定标变换,得到小参数信号;

(2)参数初始化。对所需参数进行初始化,并调节其初始范围和间隔;

(3)计算输出。根据四阶龙格-库塔法变步长求解系统方程输出,并由式(21)求解相应的SNR;

(4)获得最佳参数。结合蚁群算法,获取最大SNR及最优参数所在范围。若满足范围条件,执行下一步骤。否则,执行上一步骤(3);

(5)信号后处理。通过把最优参数引入时延欠阻尼随机共振系统,获得输出图像,并进行信号的分析和故障诊断。

2 仿真分析

为了证明时延欠阻尼三稳态随机共振方法的有效性和实用性,笔者采用该方法处理一个模拟的轴承微弱故障信号。模拟故障信号的表达式为:

(22)

式中:A—信号振幅;f—调制频率;t—采样时间;d—代表衰减率;n(t)—控制周期脉冲,n(t)=[t/Td];Td—脉冲时间间隔;D—噪声强度;ξ(t)—高斯白噪声。

模拟信号的输出如图6所示。

图6中,一个无噪信号得到的时域波形如图6(a)所示,模拟信号的时域波形如图6(b)所示,对模拟信号进行处理后获得的频谱如图6(c)所示。由于噪声干扰的存在,无法找到其中的信号频率。为了识别故障信号,进一步处理模拟信号得到包络频谱如图6(d)所示。但同样无法找到故障信号频率。由此可见,很难用包络谱来判断模拟信号的故障。

将模拟信号输入到3种随机共振系统中,得到的时域波形和频谱如图7所示。

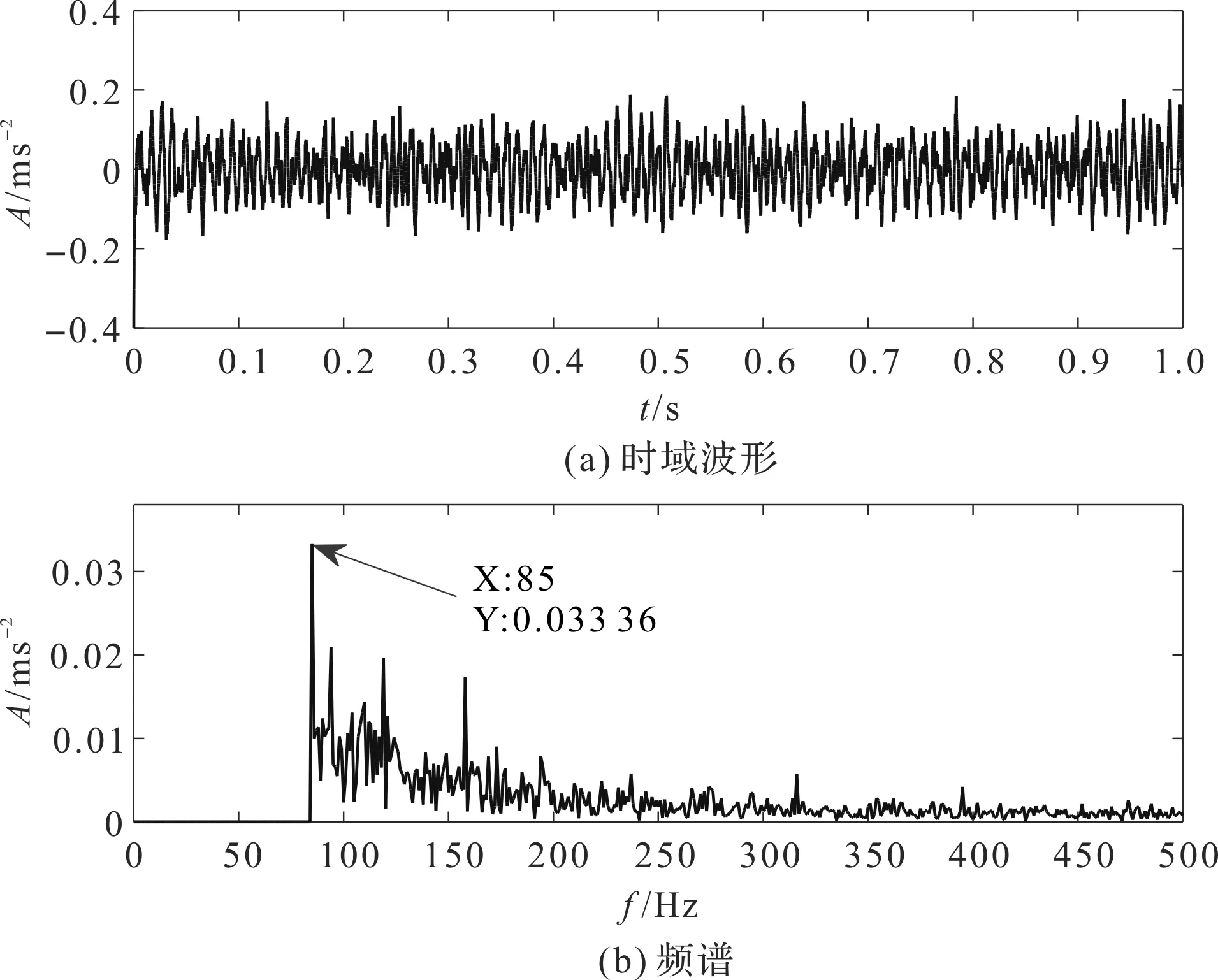
其中,图7(a,b)代表经典时延反馈随机共振方法;图7(c,d)展示经典欠阻尼随机共振方法;图7(e,f)表示时延欠阻尼三稳态随机共振方法。

从图7(b,d,f)可知,时延欠阻尼三稳态随机共振方法的目标信号频率更加明显,证明了其高频噪声得到了有效滤波。

另外,笔者采用目标信号频率的振幅大小,来对比3种随机共振方法在微弱故障信号方面的提取结果。其中,0.033 36、0.075 07两值分别是经典时延反馈随机共振方法的振幅值、经典欠阻尼随机共振方法的振幅值,而时延欠阻尼三稳态随机共振方法的振幅值是0.124 3。

由上述分析可以得出结论,即在同一故障信号频率的提取上,该方法的特征识别值更优,辨识能力更为显著。

3 实验验证

作为精密的旋转机械元件,滚动轴承在长期工作中会导致其部件的磨损。为了更好地说明3种随机共振方法的优劣,此处笔者以实际轴承故障的相关实验对此进行验证。

实验时,设备处于隔音、减振效果较好的房间,设备本身配有防护罩、且底座安装有减振器,以消除环境振动的影响。另外,实验的环境温度为室温;并考虑了轴承的润滑条件;采集单个测点的轴承内圈故障数据。

机械设备故障综合测试台,即此处的轴承综合故障测试台如图8所示。

图8 机械设备故障综合测试台

实验中所涉及的数据包括:轴承类型为ER-16K,采样频率为5 120 Hz,转速为1 800 r/min,滚珠数9,滚动体直径7.9 mm,轴承节径38.5 mm,轴承接触角α=0°。

该轴承的内圈频率计算公式为:

(23)

式中:n,fr,d,D,α—滚珠数、轴的转频、滚动体直径、轴承节径、轴承接触角。

根据以上各参数,通过计算可得到轴承内圈故障频率为162.7 Hz。

转速为1 800 r/min的轴承内圈故障信号,即其振动数据的时域波形、频谱和包络频谱如图9所示。

图9 转速为1 800 r/min的轴承内圈故障信号

从图9(b)中无法找出与轴承故障相关的信号频率;由图9(c)可知,轴承内圈的信号频率在包络谱中有明显的振幅,但其他干扰频率的振幅值也很大,因而会影响对轴承内圈故障的诊断。

因此,笔者采用时延欠阻尼三稳态随机共振方法来提取滚动轴承的故障信号频率[29,30],并采用3种不同的方法进行信号处理。

采用3种随机共振方法所得的时域波形和频谱,如图10所示。

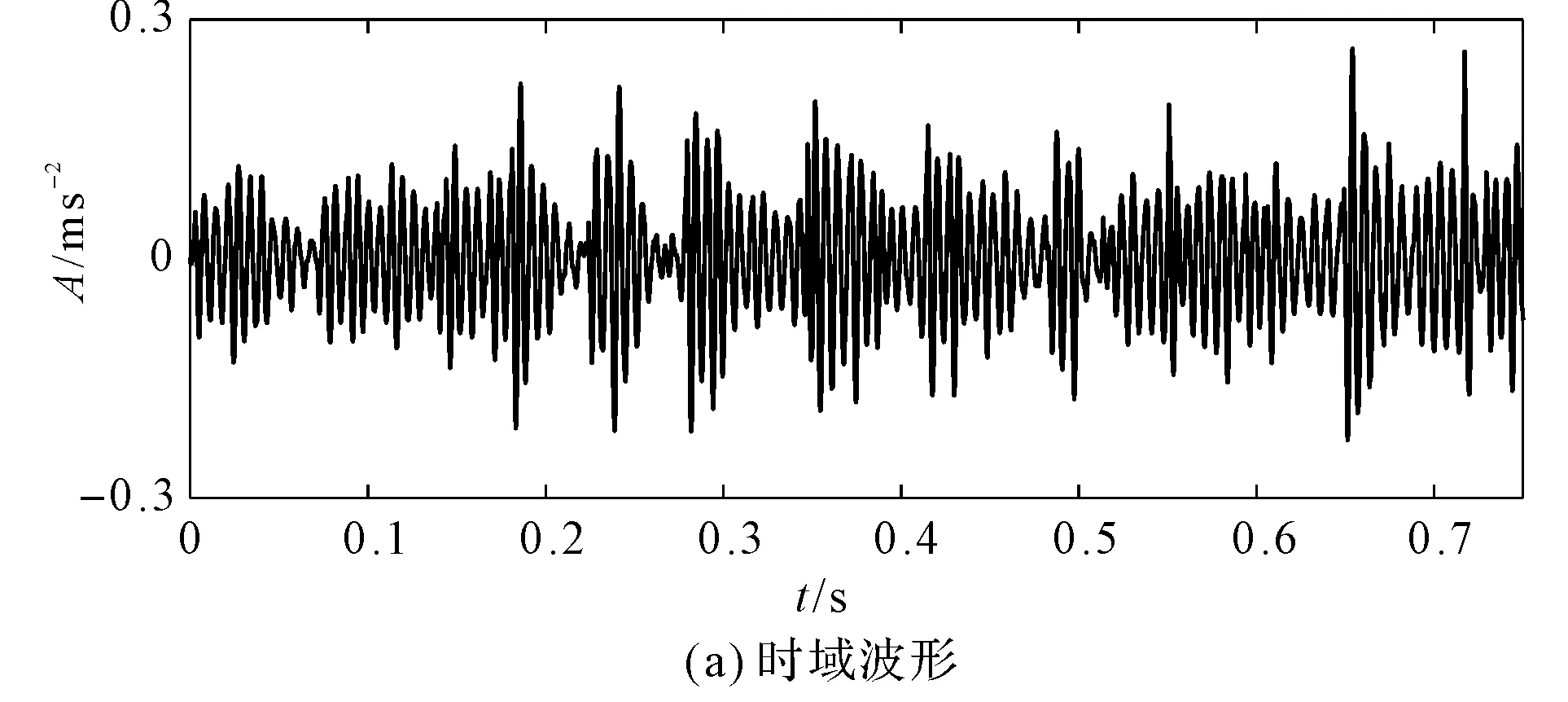
由图10可知:由3种方法的频谱可得轴承故障信号的频率都为162.6 Hz,接近理论公式推导的值162.7 Hz。

笔者把故障信号频率与噪声的振幅之间的差作为识别指标,对3种方法进行了对比:(1)经典时延反馈随机共振方法的振幅为0.061 59,识别效果为0.027 33;(2)经典欠阻尼随机共振方法的振幅为0.075 83,识别效果为0.049 65;(3)时延欠阻尼三稳态随机共振方法的振幅为0.145 5,识别效果为0.115 47。

以上对比结果表明,基于时延欠阻尼三稳态的随机共振方法具有良好的故障诊断效果,也验证了该方法的优越性。