电子水阀结构优化仿真及其试验研究*
2021-11-27王宏伟曹淼龙杨元健
张 波,张 莉,王宏伟,曹淼龙,杨元健
(1.浙江科技学院 机械与能源工程学院,浙江 杭州 310023;2.台州学院 智能制造学院,浙江 台州 318000;3.浙江银轮机械股份有限公司,浙江 台州 317200)
0 引 言
电子水阀是一种新型的冷却液流量调节阀,是新能源汽车热管理系统的核心零部件之一,其主要作用是调节不同管路冷却液的流量大小,将各工作部位的温度控制在合适的范围内,以实现节能减排和能量有效利用的目的。
流量调节阀是工业控制系统中的关键器件。常见的流量调节阀有:球阀、三通阀、旋转阀和蝶阀等[1]。
目前,国内外专家学者已经对流量调节阀做了大量的研究。MOUJAES S F等人[2,3]对湍流状态下不同阀门开度的调节阀进行了压降仿真分析,并通过实验对其仿真结果进行了验证。LISOWSKI E等人[4,5]基于CFD,针对不同结构参数的调节阀在不同工况下的调节特性进行了分析,并通过实验对其分析结果进行了验证。张立强等人[6]分析了不同开度下,调节阀的压力场和速度场,并对阀内发生空化现象的区域和空化强度进行了初步的分析和预测。金伟等人[7]对旋转调节阀的工作原理,以及阀芯旋转过程中阀体内部的流动特性分别进行了详细研究。
三通阀是流量调节阀中最常见的一种。按其作用形式的不同,三通阀可分为两种:合流阀和分流阀[8,9]。三通调节阀能够对不同管路的流量特性进行调节,可以替代2个二通阀和1个三通接管,因此,其既可减少成本,又可以降低系统的复杂度。
目前,对三通调节阀的研究主要侧重于对其结构优化与流动特性的分析。李树勋等人[10]运用遗传优化算法,确定了三通调节阀节流盘的开口型线,并对其进行了数值模拟分析和试验验证。靳淑军等人[11]运用CFD软件对三通调节阀内部流道进行了数值模拟,探究了上、下阀座压力梯度和速度梯度随阀门开度的变化规律。章茂森等人[12]对三通调节阀内部湍流进行了三维数值模拟,分析了不同工况下阀芯节流锥面对内部湍流动能和耗散率的影响。孙彩珍等人[13]对三通调节阀进行了流场的流动特性分析,并通过测试试验和对比分析的方法,研究了调节阀内部流动特性的变化规律。
压降是衡量电子水阀使用性能的一个重要指标。压降过大会导致整个热管理系统的冷却液循环动力不足,从而使电机、电池等发热严重部位的热量无法及时带走,引发高温故障,导致车辆无法正常使用。
本文以现有电子水阀为研究对象,根据影响压力损失的结构因素变量设计正交试验,采用数值模拟与试验相结合的方法对优化前后的结构进行压降和流动特性分析,研究电子水阀不同阀门开度下的流场压力分布和流速变化规律,为调节类阀门的优化设计提供参考。
1 流道结构参数优化
1.1 流道结构及其工作原理
电子水阀的流道结构由1个入口管道、2个出口管道以及阀芯组成,电子水阀及其流道结构剖面示意图如图1所示。

图1 电子水阀及其流道结构剖面示意图A—管道直径;B—入口缩角;C—出口扩角;D—阀芯流道转角
电子水阀的工作原理:将ECU采集的温度数字信号转换为模拟信号,驱动电机带动阀芯转动,通过改变阀芯与进出口管道之间的相对位置,实现对不同管路的冷却液进行流量调节。
在初始状态(阀芯旋转0°)时,默认旁通阀门为全开,直通阀门为全闭;在阀芯顺时针旋转过程中,旁通阀门逐渐闭合,直通阀门逐渐打开,直至完全开启。
电子水阀传统流道结构参数如表1所示。

表1 传统流道结构参数
1.2 流道结构参数优化
1.2.1 多因素正交试验
由流道的结构组成可知:影响压力损失的主要因素为管道直径、入口缩角、出口扩角和阀芯流道转角。但由于涉及影响因素较多,利用单因素逐一试验法无法确定流道最优结构参数。
在传统流道结构参数设计的基础上,笔者利用Design-Expert优化设计软件,设计多因素正交试验。
仿真试验因素与水平如表2所示。
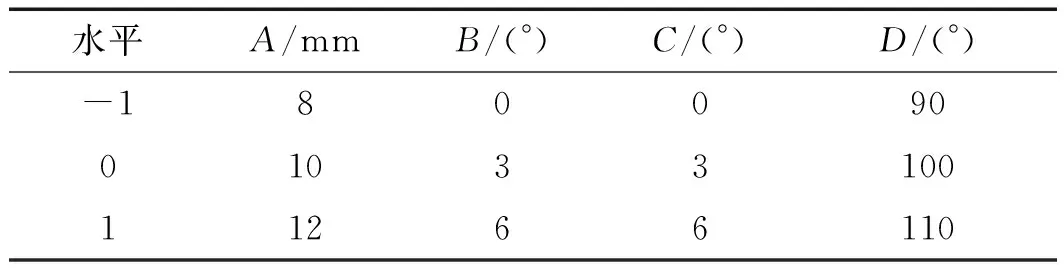
表2 仿真试验因素与水平
1.2.2 优化结果分析
笔者根据正交试验设计生成的变量组合进行数值模拟试验,以10 L/min时的旁通压降Δp和最小流通面积S作为优化目标;根据试验数据样本,通过优化软件,拟合出编码后的旁通压降和最小流通面积的二次多项式回归模型,即:
Y1=3.47-3.26A+0.87B-0.17C+0.83D-0.2AB-
0.12AC-1.29AD-0.096BC-0.053BD-
0.57CD+1.67A2-0.45B2-0.54C2+0.52D2
(1)
Y2=29.36+33.74A-0.038B+0.073C+6.32D+
0.004 83AB+0.068AC+2.33AD-
0.065BC-0.004 83BD+0.28CD+
8.82A2+0.12B2+0.09C2+0.34D2
(2)
式中:Y1—旁通压降;Y2—最小流通面积;A—管道直径;B—入口缩角;C—出口扩角;D—阀芯流道转角。
根据回归模型,笔者利用优化设计软件绘制出各因素交互效应3D响应曲面,如图2所示。

图2 各因素交互效应3D响应曲面
由图2可知:对旁通压降有显著影响的因素为管道直径、入口缩角和阀芯流道转角,出口扩角对其影响略小;对最小流通面积有显著影响的因素为管道直径和阀芯流道转角(没有影响或影响较小的因素未在图中列出);
由图2还可知:在管道直径增大的过程中,入口缩角越大,压降越大;出口扩角越小,压降越大;流道转角越大,压降越大;流道转角越大,最小流通面积越大。
1.2.3 最优参数选择
流道最优结构参数的选择原则是:(1)压降最小;(2)最小流通面积在合适范围内。因此,笔者以旁通压降1.5 kPa、最小流通面积范围60 mm2~80 mm2为条件,通过模型求解,得出了其最优的结构参数如下:
管道直径A为11.93 mm,入口缩角B为0.05°,出口扩角C为5.94°,阀芯流道转角D为90.06°。
优化后的流道结构示意图如图3所示。
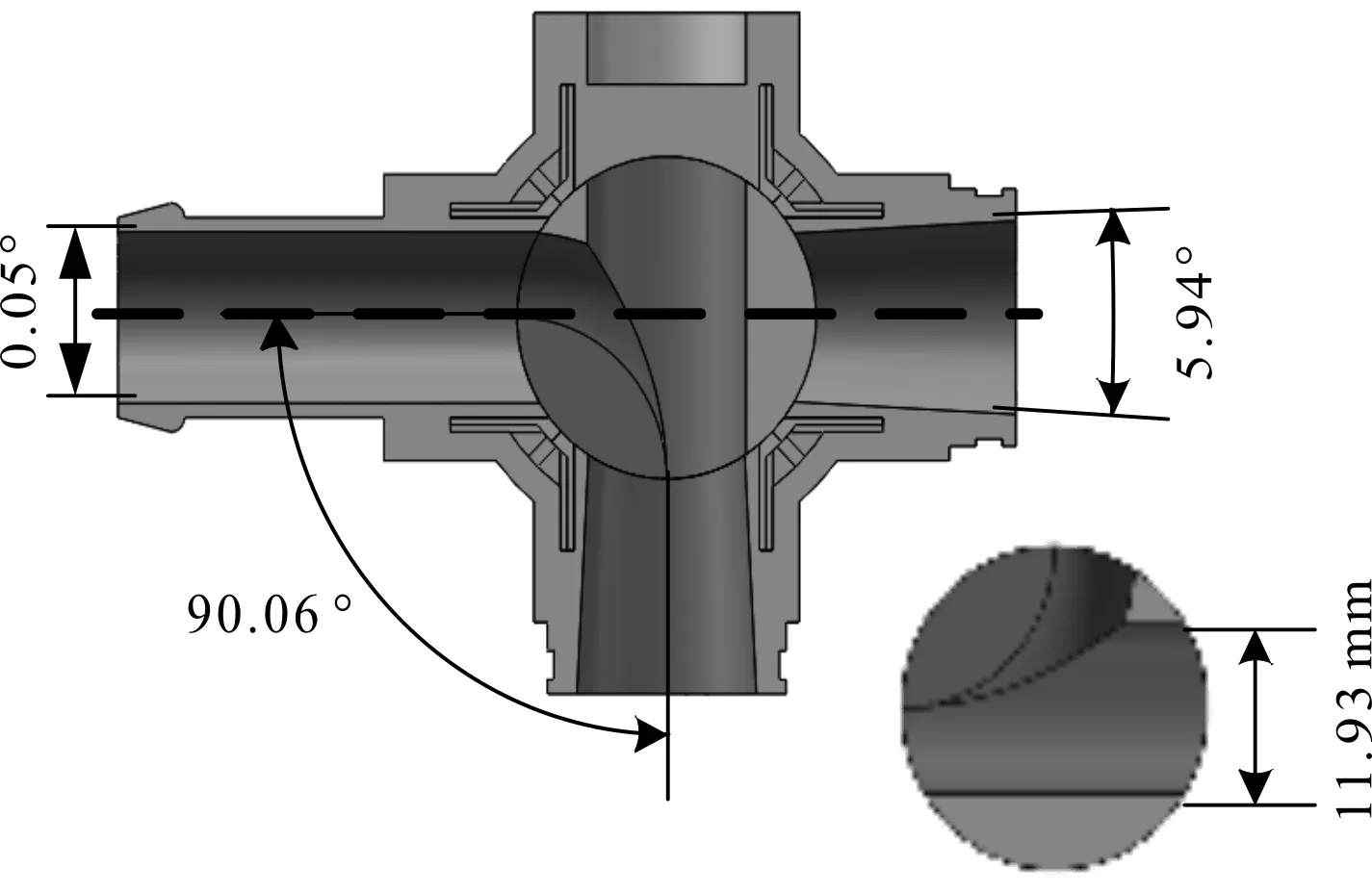
图3 优化后的流道结构示意图
2 结构优化前后流场仿真分析
2.1 物理模型
为分析优化前后电子水阀的压力损失情况和流场流动特性变化规律,笔者对不同阀门开度下的流道结构进行三维建模分析。为减小回流的影响,此处将进口管道设置为管径的5倍,出口管道设置为10倍。
阀门开度为45°时的流体域模型如图4所示。
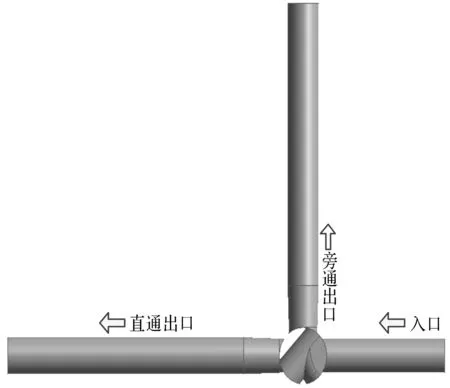
图4 流体域模型
2.2 网格模型
网格划分的目的是使模型实现离散化,把求解域分解成适当数量,可得到精确解的单元。节流口处压力和速度梯度变化较大,需对其进行网格加密处理,以提高其仿真分析的精度。
笔者通过ANSYS Workbench的模块Mesh对模型进行网格划分,划分后的网格模型如图5所示。
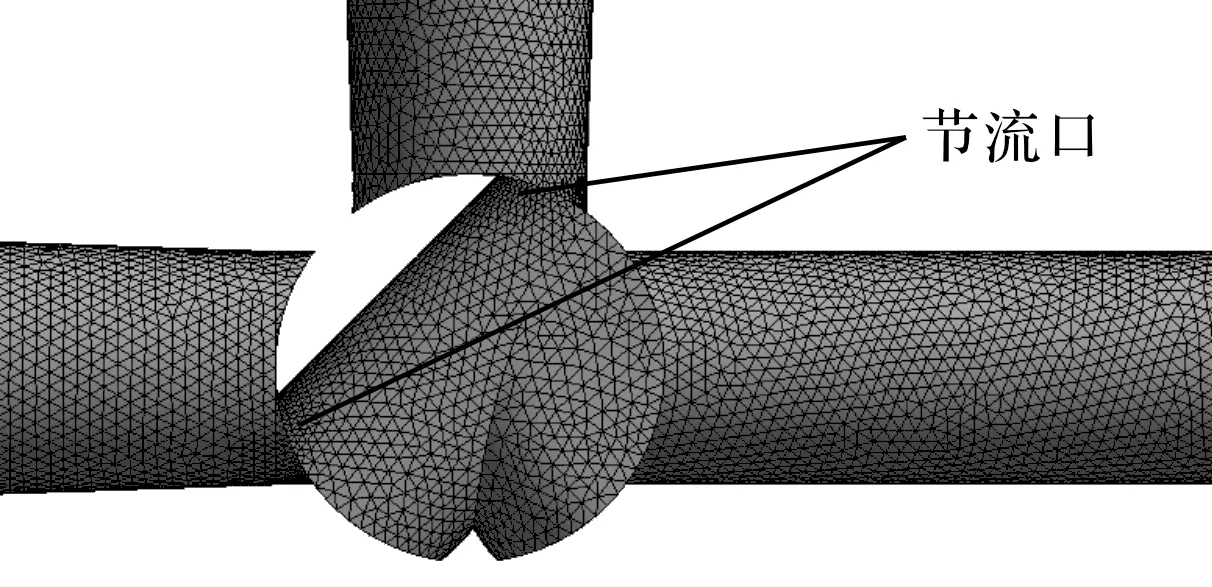
图5 流体域局部网格模型
图5中,划分后的网格经过质量检查,网格平均质量为0.85左右,网格平均偏斜度为0.2左右,符合Fluent的求解要求。
2.3 网格无关性验证
在数值模拟计算过程中,由于网格的数量和质量直接决定了计算结果的准确性,在网格质量已经满足计算要求的前提下,需要对网格数量n进行无关性验证。
笔者以10 L/min时,直通出口的质量流量q(kg/s)作为验证目标,进行网格无关性验证。
验证结果如表3所示。

表3 网格无关性验证结果
表3中,当网格数量达到6.3×105以上时,直通出口的质量流量基本达到稳定。因此,本次研究选择的网格数量为6.5×105左右。
2.4 求解器设置
在Fluent求解器中,模型选择标准k-ε湍流模型,壁面函数选择Standard Wall Function,流体介质为50%的水-乙二醇混合溶液,密度ρ为1 071.11 kg/m3,动力黏度μ为0.003 39 kg/(m·s-1);
边界条件选择速度入口和压力出口,设置出口压力等于大气压力,速度与压力耦合的求解方法选择SIMPLEC算法。
速度与流量之间的关系如下:
(3)
式中:v—平均流速,m/s;Q—流体进口流量,m3/s;d—管口内径,m。
2.5 优化前后压降仿真分析
此处笔者对优化前后的直通和旁通阀门分别进行压力场的仿真分析。
在流量为10 L/min时,直通阀门优化前后对称面压力云图如图6所示。
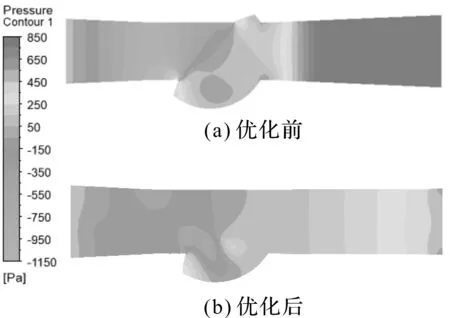
图6 优化前后直通压力云图
在流量为10 L/min时,旁通阀门优化前后对称面压力云图如图7所示。
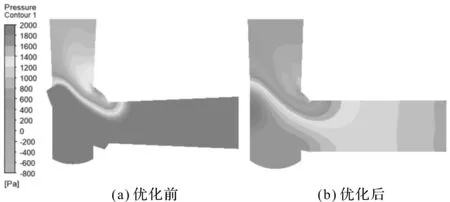
图7 优化前后旁通压力云图
由图6和图7的仿真云图可以看出:优化前的高压区出现在入口管道和阀芯处,当溶液流过阀芯转角后,其压力迅速降低。
压力损失的原因有:(1)入口管道为渐缩结构,不仅增加了流体与管壁的接触面积,导致流阻增大,而且还会使流速增大;(2)阀芯与出口管道连接处为突扩结构,当流体流过时会发生分离,再加上流速过大,流体与管道产生激烈碰撞,导致压力损失严重。
由上述仿真云图还可以看出:(1)经过优化后,直通全开时的最大压力由2.5 kPa减小至1.1 kPa,最小压力由-2.3 kPa增加至-0.32 kPa;(2)旁通全开时的最大压力由5.8 kPa减小至2.5 kPa,最小压力由-2.8 kPa增加至-1.3 kPa;(3)阀内压力梯度分布更加均匀,压力损失情况得到明显改善。
经过计算可知,在优化后,直通和旁通阀门全开时的压降较优化前分别降低了63%和54.3%。
2.6 优化前后水阀内部流动特性分析
2.6.1 分流特性分析
为探究电子水阀优化前后的分流特性,笔者选择旁通分流比作为研究对象。旁通分流比随阀门开度变化曲线如图8所示。
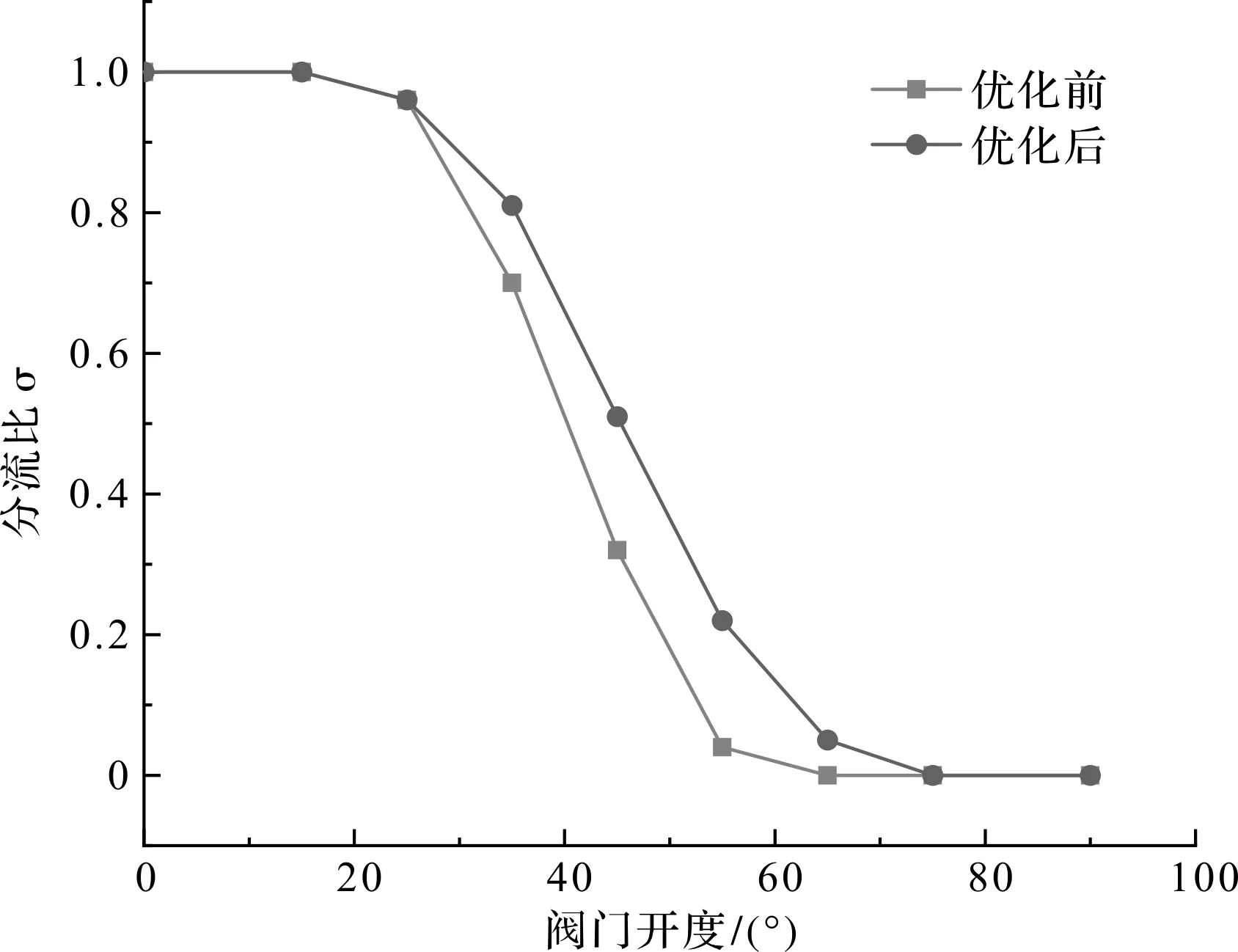
图8 优化前后旁通分流比随阀门开度变化曲线
从图8中可以看出:优化前后的旁通分流比均随阀门开度的增大而减小,且与阀门开度之间为非线性关系。经过优化后,电子水阀的有效分流角度由15°~65°扩大至15°~75°,旁通分流比随阀门开度变化曲线相较于优化前更加平缓,不同阀门开度下的流量分配更加均匀。
2.6.2 压力场分析
为分析优化前后电子水阀的流场压力变化规律,本文选取10 L/min时25°、45°、65°开度下的压力场进行分析。
优化前后,不同阀门开度下最大压力的变化曲线如图9所示。

图9 优化前后最大压力随阀门开度变化曲线
由图9可知:经过优化,不同阀门开度下的最大压力得到明显降低,压力梯度分布更加均匀;且低压区域减小,降低了阀内空化发生的可能性。
优化前后,不同阀门开度下对称面压力云图如图10所示。
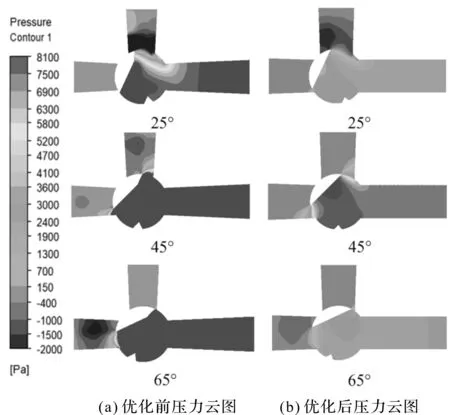
图10 优化前后不同阀门开度下压力仿真云图
从图10的压力仿真云图中可以看出:优化前后,流道内整体的压力分布趋势相似,进口管道和阀芯内为高压区,当流体流经节流口时压力迅速降低,并在靠近节流口的出口管道一侧形成负压区;然后,在出口管道下游,压力又逐渐升高。
出现这种趋势的原因在于:随着阀门开度增加,节流口处流通面积先减小后增大,在45°时流通面积最小,所以高压区出现在进口管道和阀芯内。高压区的产生会导致节流口处流速较大,流体流经节流口时发生流动分离,导致压力迅速降低,使此处易发生空化现象[14-17];随后,流速趋于平缓,压力逐渐恢复。
2.6.3 速度场分析
为分析优化前后电子水阀流场速度变化规律,本文选取10 L/min时25°、45°、65°开度下的速度场进行分析。
优化前后,不同阀门开度下最大速度变化曲线如图11所示。
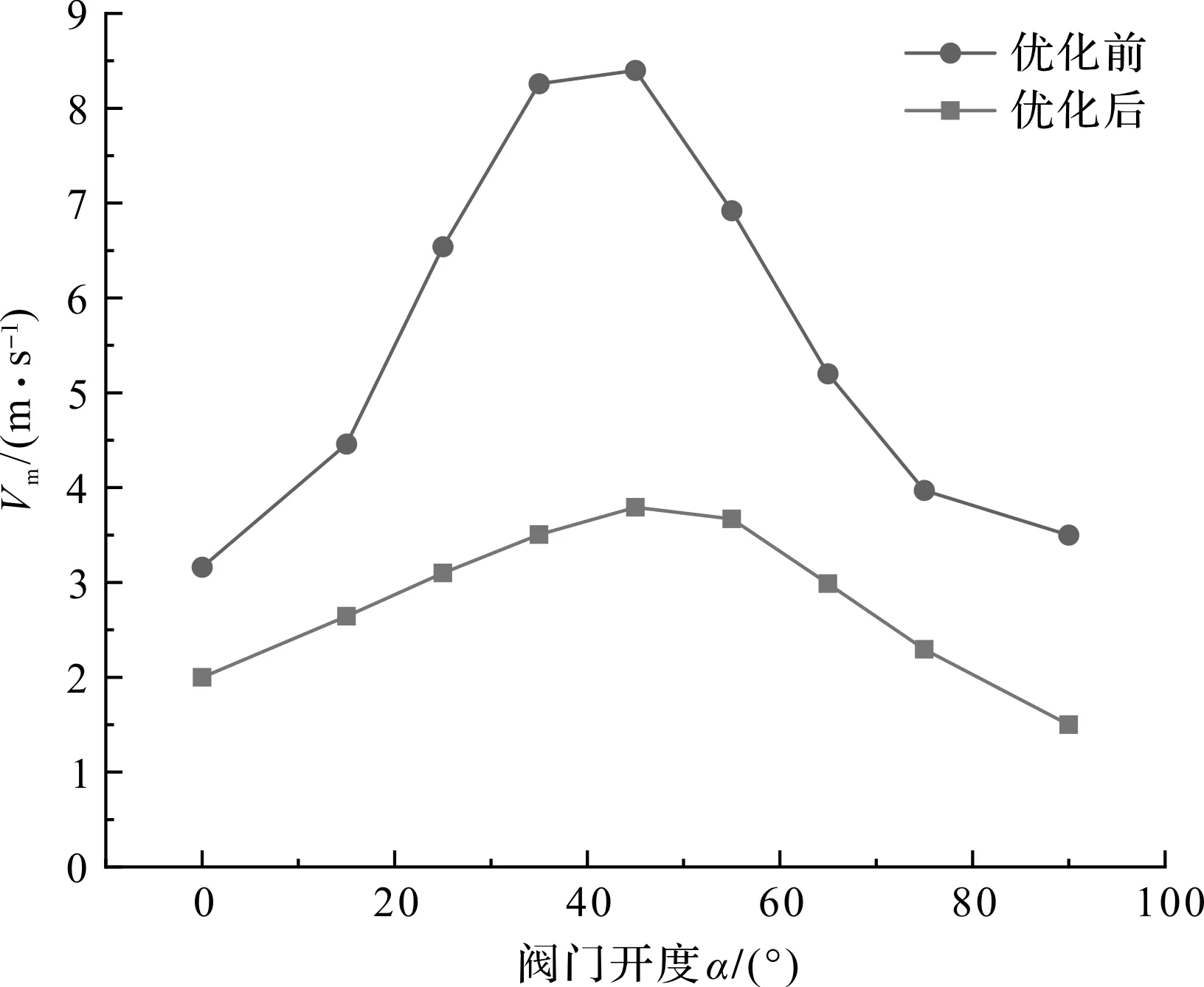
图11 优化前后最大速度随阀门开度变化曲线
优化前后,不同阀门开度下对称面速度云图如图12所示。

图12 优化前后不同阀门开度下速度仿真云图
由图11可知:当流体流经节流口时,由于流通面积减小,会在节流口处形成高速流,且最大流速随阀门开度的增加,呈现先增大后减小的趋势,在45°时流速最大。流速过高不仅会导致流体在节流口处分离严重,还会使流体在高速流附近形成涡流。
涡流的产生,一方面增加了流体的流动阻力,导致局部压力损失过大;另一方面,也是产生噪声、振动的重要原因[18,19],对产品的使用性能有严重影响。
经过优化后,不同阀门开度下的最大流速明显减小,最大流速变化曲线也趋于平缓,并一定程度上降低了噪声和振动对电子水阀性能的影响。
3 试验验证
3.1 试验方法
为验证优化后电子水阀的压降,笔者对电子水阀进行压降测试试验。试验方法为在电子水阀进出口外接管两端安装压差传感器(精度1 Pa),通过一定工况冷却液流量,记录压差数据a;同时,笔者选取与电子水阀进出口两端相同长度的外接管,安装压差传感器,通入相同工况的冷却液流量,记录压差数据b(电子水阀测试压降a减去两端多余外接管路压降b,即为其实际的压降)。
压降试验原理图如图13所示。
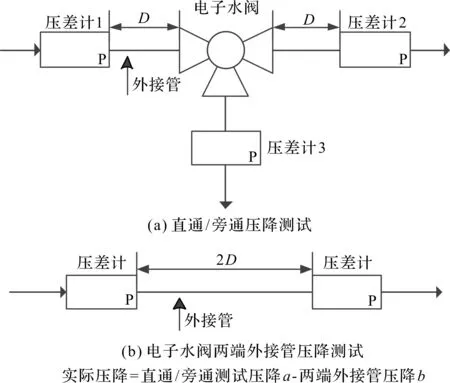
图13 压降试验原理图
压降测试试验台的实物图如图14所示。

3.2 结果分析
根据试验结果,笔者绘制了直通和旁通阀门优化前后不同工况下的压降变化曲线。其中,不同工况下直通优化前后压降变化曲线如图15所示。
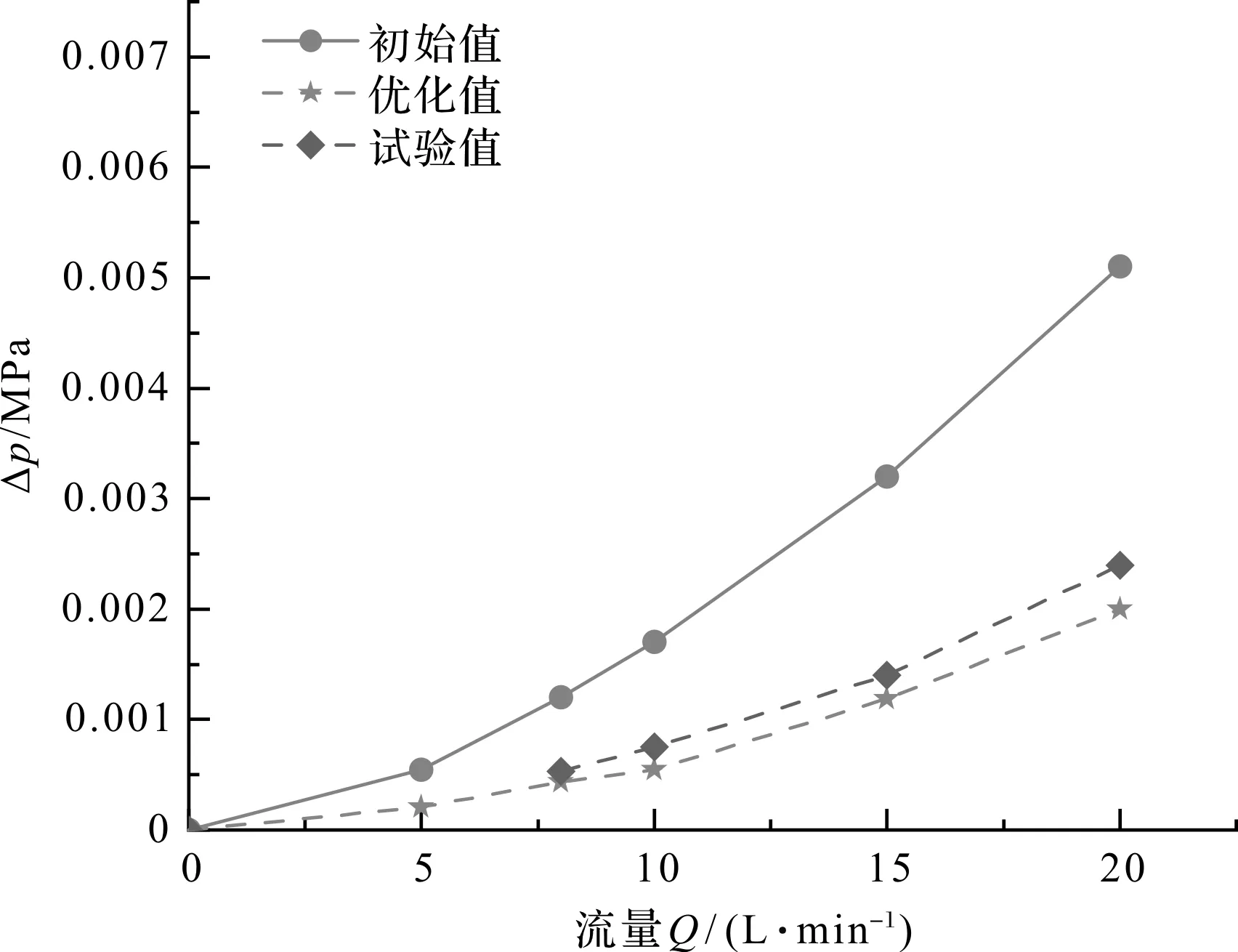
图15 不同工况下直通优化前后压降变化曲线
不同工况下旁通优化前后压降变化曲线如图16所示。
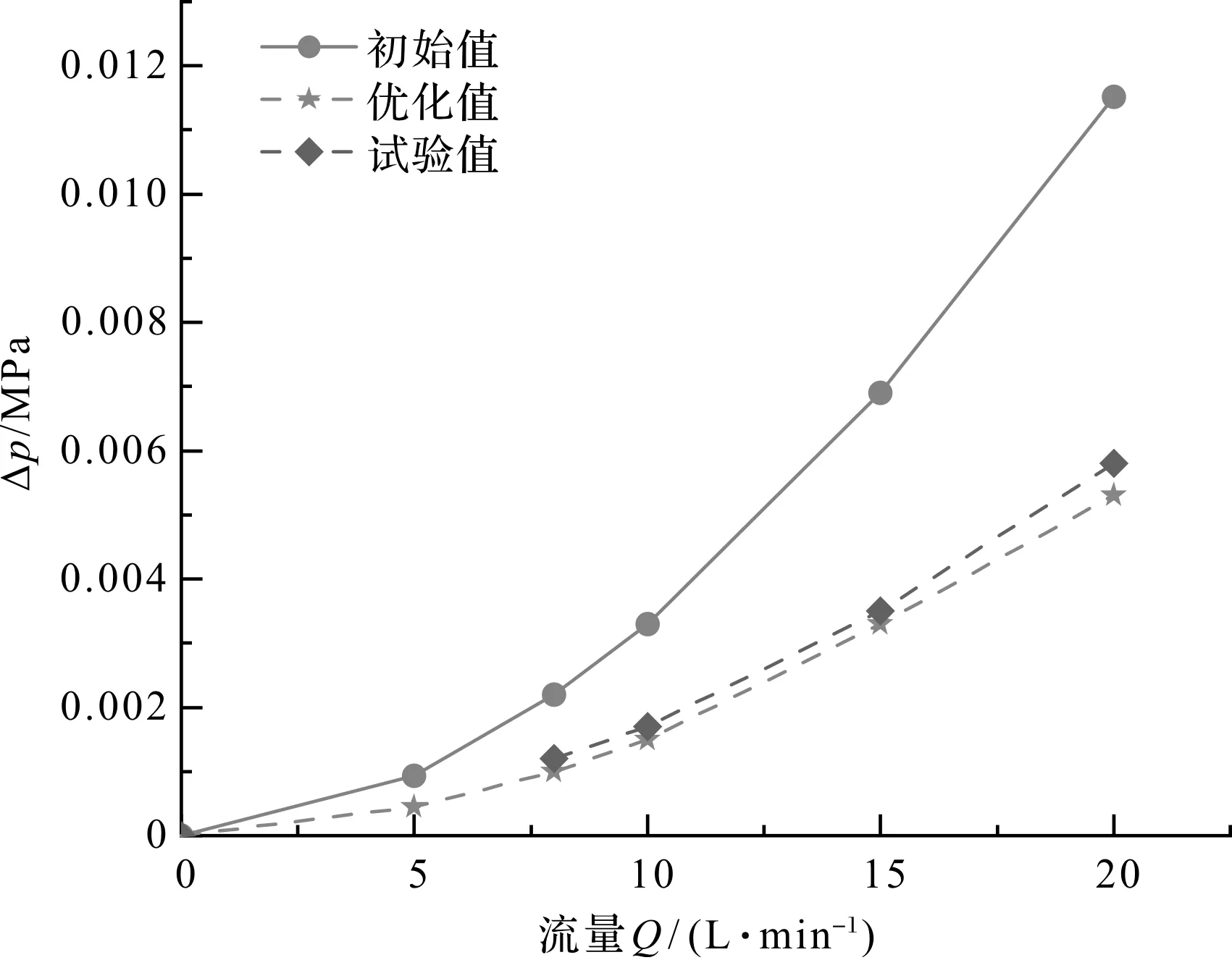
图16 不同工况下旁通优化前后压降变化曲线
通过以上的压降变化曲线图可以直观地看出:相比于优化前的结果,优化后的压降测试结果有了明显减小;经过计算,直通和旁通测试压降较优化前最大可分别降低57.5%和49.9%。
由于仿真模型为理想模型,不考虑间隙泄漏和制造工艺精度等影响因素,优化值与试验值存在一定误差,仿真值与试验值的最大相对误差在15%以内,符合设计要求。
4 结束语
根据对影响电子水阀压力损失的结构因素进行分析,笔者利用Design-Expert软件设计了流道结构的多因素正交试验,采用数值模拟的方法对水阀优化前后的压降和流场流动特性进行了仿真分析,最后通过水阀压降测试试验对上述仿真结果进行了验证。
研究结论如下:
(1)经过结构优化后,电子水阀的压力损失情况有了明显改善;经过仿真分析结果显示,直通和旁通全开时的压降最大可分别降低63%和54.3%;经过试验测试,直通和旁通全开时的压降最大可分别降低57.5%和49.9%,试验值与仿真值的相对误差在15%以内,验证了仿真结果的正确性;
(2)通过对旁通分流比特性曲线分析可知,旁通分流比与阀门开度之间为非线性关系;经过优化后,电子水阀的有效分流角度由15°~65°扩大至15°~75°,旁通分流比随阀门开度变化曲线更加平缓,不同阀门开度下的流量分配更加均匀;
(3)通过对优化前后不同阀门开度下的流场流动特性分析可知,不同结构参数对流体的流动特性有重要影响,直接决定着电子水阀的使用性能;经过优化后,电子水阀内压力分布和流速变化情况得到了显著改善,使用性能得到了大幅提升。
在后续的研究中,笔者将主要开展研究工作:(1)电子多通阀的设计与研究,即将现有热管理系统中使用的多个电子水阀合为一体,集中调节各管路冷却液流量;(2)实现电子水阀、电子水泵和水壶等结构的模块化,以降低系统复杂度,提高其热管理效率。
