自适应定阶的快速Burg 算法设计与FPGA 实现*

郭鸣晗 ，陈立平 ，张 浩 ，赵 坤 ，柏 伟

(1.中国科学院大学，北京 100049；2.中国科学院微电子研究所，北京 100029)

0 引言

现代功率谱估计的AR 模型法使用有限长的数据序列来估计假设模型的参数，再将参数带入功率谱密度模型中，可获得较好的功率谱估计结果[1-3]。

Burg 算法是一种常见的AR 模型求功率谱的方法，其主导思想是利用前后向预测误差功率之和最小的方法来计算反射系数k，然后带入Levinson 递推，求解AR模型参数[4-6]。此方法在处理短数据时具有较高的频率分辨率[7-8]，但求解反射系数计算量较大。为了改进这一问题，Vos 提出一种快速Burg 算法[9]，通过一系列矩阵变换降低了反射系数求解时的计算量，但是不能确定AR模型的阶数，并且串行算法的执行耗时较长。针对上述问题，本文将快速Burg 算法与FPE 准则[10]结合，对短序列的功率谱估计实现自适应定阶的功能，达到较高频率分辨率，并使用Verilog 硬件描述语言设计电路，达到硬件加速功能[11]。电路结构在二级流水线的基础上[12]，结合自适应定阶方案，提出一种新的流水线结构，并设置状态机灵活控制。本文对计算单元进行并行化处理加速计算。考虑速度与面积的折中，针对算法特点设计内存读写方案，减少数据存储长度，从而减小了存储单元的面积。

1 自适应定阶的快速Burg 算法

快速Burg 算法过一系列矩阵变换将反射系数计算过程化简[9]，避免了Burg 算法[4]中计算反射系数前需计算出前、后向预测误差ef、eb而带来的较大计算量。在本算法中，通过自适应定阶的方式，对长度为N 的输入序列xn的递归计算步骤如下：

(1)计算自相关ci。(本实验中自适应定阶在10 阶以内，在此只计算10 个自相关值)。

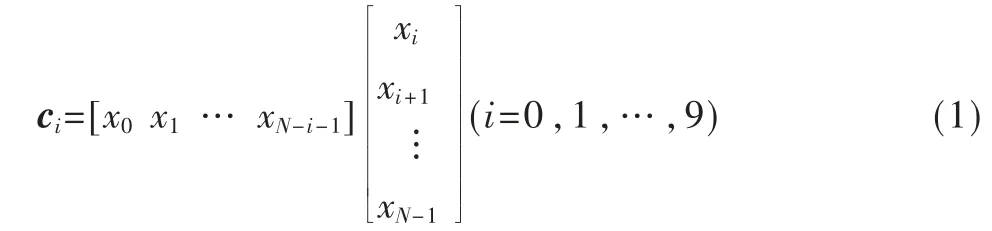
(2)初始化。初始为第一阶，此时迭代次数i=0；用于计算反射系数的列向量g0=[2c0-|x0|2-|xN-1|2；2c1]T；用于计算列向量gi的列向量r1=c1；预测系数a0=1；反射系数。

(3)计算初始预测误差功率Pmin(0)，预测误差FPE 值和初始阈值TH：

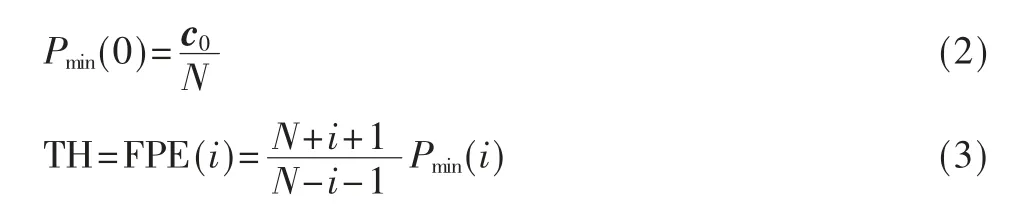
(4)判断迭代条件(TH＜FPE(i))，即若满足阈值TH 小于预测误差FPE 值，则将当前阈值TH 更新为预测误差值TH=FPE(i)，之后i+1，继续执行步骤(5)；若不满足，则计算阶数，输出预测系数ai。

(5)更新列向量ri+1：

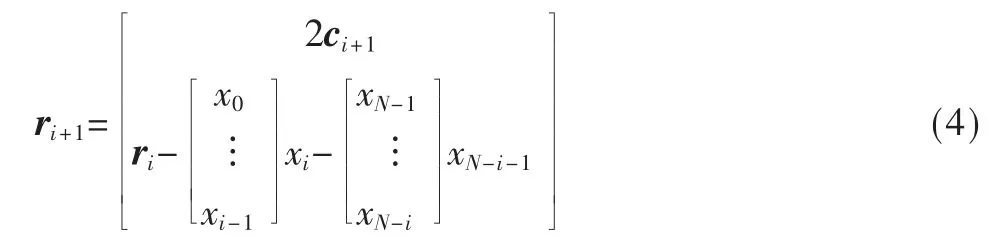
(6)更新用于计算列向量gi的矩阵：

(7)更新列向量gi：

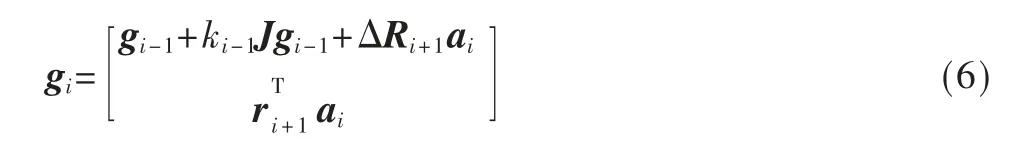
其中，J 是i+1 行的方阵：

(8)计算初始反射系数：

(9)计算最小预测误差功率Pmin(i)与最终预测误差准则中的FPE(i)值：

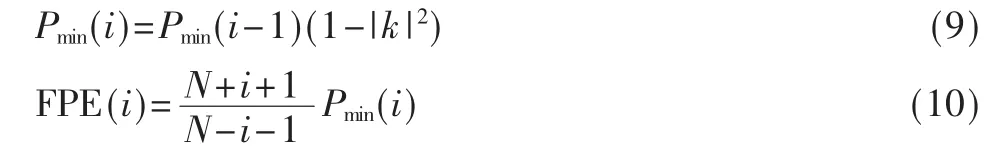
(10)更新AR 模型参数ai，跳转到步骤(3)。

2 硬件电路设计与实现

2.1 并行二级流水线结构

本算法完成硬件加速的关键思路是使用流水线的结构。自相关ci的计算只和输入序列xn有关，与AR 参数的计算无关，而AR 参数的计算需要利用自相关的值，故电路结构将划分为二级流水线，第一级为自相关ci的计算，第二级为AR 参数和阈值的计算。为了提高计算速度，本设计将采用并行的二级流水线结构，时序关系如图1 所示。

图1 并行二级流水线时序图

本电路结构的顶层电路图如图2 所示，计算单元由两个并行连接的自相关计算单元和AR 参数、阈值计算单元构成，控制单元为状态机来控制迭代次数以及计算单元。存储单元包括两个存放xn的RAM，宽度为16，深度为序列长度N(在本设计中N=128)，一个用于自相关计算，一个用于AR 参数计算；第二部分用来存储AR 参数、阈值计算单元产生的中间结果。

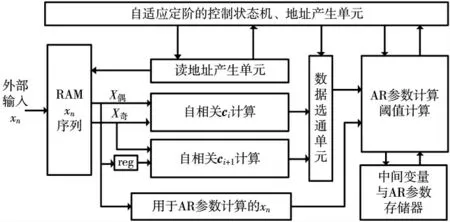
图2 快速Burg 算法顶层电路图

2.2 自适应定阶与状态机控制

为了达到自适应定阶目的和提高流水线使用效率，采用状态机来控制计算单元，根据阈值FPE 是否达到最小值来确定是否停止运算。在本算法中，AR 参数的阶数自适应得确定在2～10 阶内。

本状态机的输入信号为外部输入的算法使能信号和计算单元的结束状态标识信号，输出为计算单元的使能控制信号。

根据并行二级流水线结构和自适应定阶算法，控制单元状态机如图3 所示，共分为6 个状态。

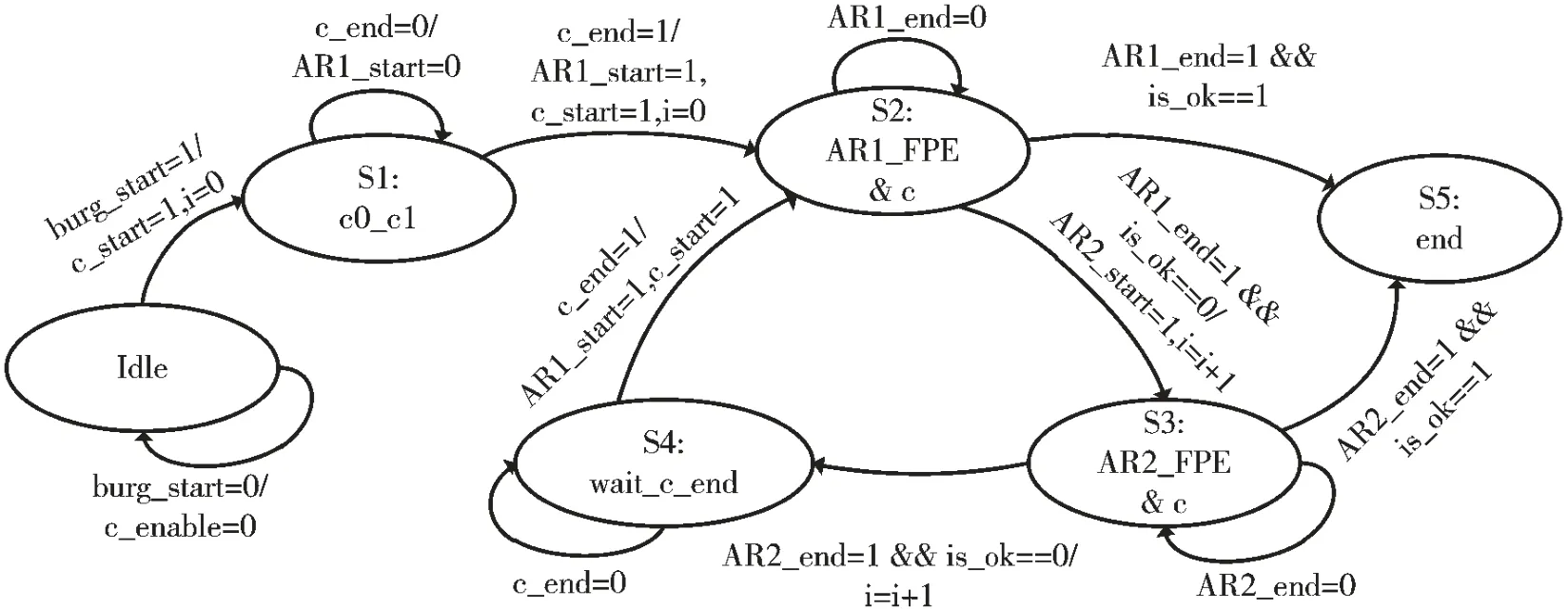
图3 快速Burg 算法控制单元状态机

算法启动后，初始阶数为1，迭代次数i=0，进入S1状态进行初始自相关计算；之后进入S2 启动后续自相关计算及AR 参数和阈值计算。计算完成后若FPE 达到最小值，跳至S5 结束运算，最终定阶为i+1 阶；否则跳转至S4，启动下一阶AR 参数模型和阈值计算。计算完成后若FPE 达到最小值，则跳转至S5 结束运算，最终定阶为i+2 阶；否则跳转至S4，等待当前的自相关计算结束后再次进入S2 进行下一轮的迭代，直至FPE 达到最小值，迭代停止，RAM 中的AR 参数即为所求。

2.3 计算单元的设计

2.3.1自相关的计算单元

自相关的计算使用流水线结构。产生地址、读取数据、乘累加运算，三拍完成一次乘累加输出，两个自相关计算单元分别进行N-i 次和N-i-1 次乘累加后，输出自相关值ci、ci+1给下一级计算单元，当前阶数下消耗的总计算时长为N-i+3 个时钟周期。

2.3.2 AR 参数和阈值计算单元

本计算单元电路包括4 个模块：预备参数计算模块、反射系数k 值和AR 参数a 计算模块、预测误差功率Pmin计算阈值计算模块，以及判断阈值是否达到最小值的定阶模块。本单元顶层结构如图4 所示。

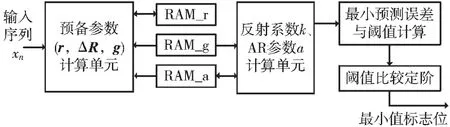
图4 AR 参数和阈值计算单元顶层电路图

快速Burg 算法的关键即为计算预备变量，包括r、ΔR和g 3 个变量。

r 列向量的计算电路为三级流水线结构，其电路如图5 所示。第一拍锁存当前阶数下输入序列的第一个乘数，并将读入的数据写入Xf_buffer 和Xb_buffer；第二拍并行完成两次乘加运算；第三拍做选通输出c1或乘加值，并倒序输出r 列向量的行值。当前阶数下消耗的总计算时长为i+3 个时钟周期。

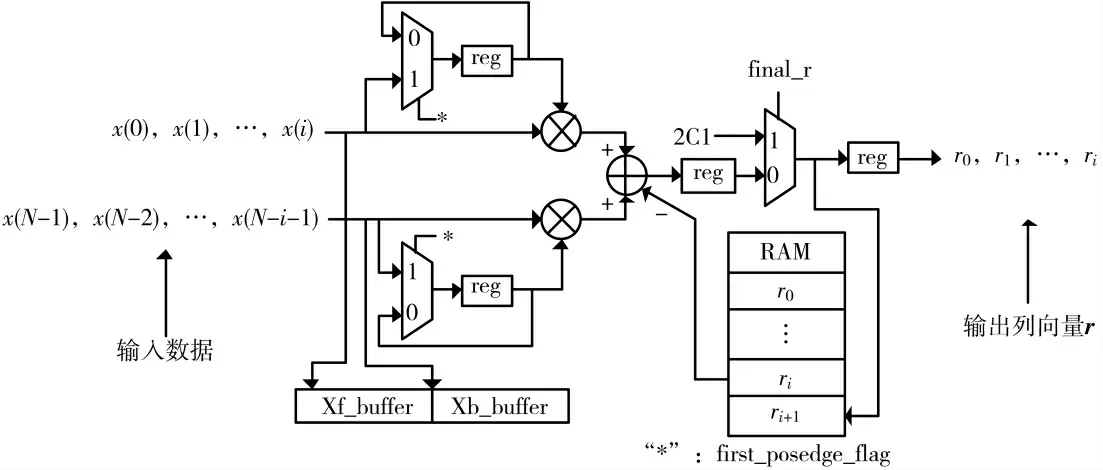
图5 列向量r 的运算电路

中间变量矩阵ΔR 和列向量g 的计算电路采用并行化处理，矩阵ΔR 和列向量g 的四级流水线电路如图6所示。第一拍从两个buffer 中各依次读出一个x 值送入乘法器；第二拍做乘加运算，得到矩阵ΔR 的一行值；第三拍ΔR 的行值分别与上一阶求得的AR 参数依次相乘并求和；第四拍选通输出列向量g 的行值。当前阶数下消耗的总计算时长为i+5 个时钟周期。

图6 矩阵ΔR 和列向量g 的运算电路

2.4 存储单元设计

由于参数计算过程中部分变量需要在每阶下递归运算，因此需为其分配内存空间。为了起到加速的作用，使用双口RAM 对中间结果进行存储，提高读写数据的速度。

3 结果分析

3.1 功率谱估计的分辨率

在本节中，当输入数据采样率为512 Hz，输入数据点数为512 时，通过ModelSim 实验平台对基于定点数[13-14]的算法进行仿真，并将FFT 算法和本算法的频率分辨率进行比较。仿真实验中，AR 参数计算结果a 和最小预测误差Pmin仿真结果如图7 所示。

图7 ModelSim 仿真结果

为了更直观地观察频谱结果，将硬件电路的结果传入MATLAB 中，经过处理打印功率谱图，并将硬件电路计算出的定点数模型的功率谱结果与MATLAB 直接计算的浮点数功率谱结果进行比较，如图8 所示，谱峰一致说明量化良好。

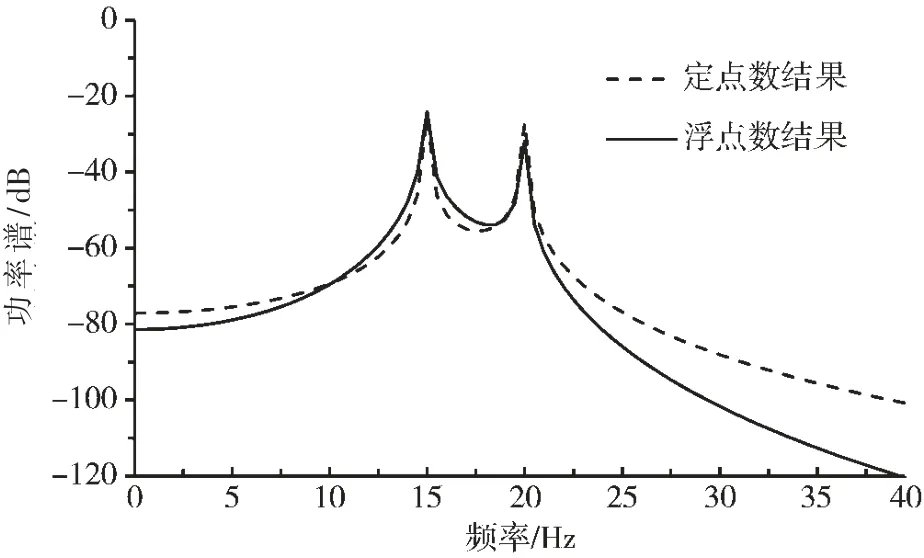
图8 定浮点算法功率谱结果比较

实验设置输入数据为15 Hz 和20 Hz 正弦波的叠加信号，采样率为512 Hz。

当输入数据长度为512 时，FFT 算法和自适应定阶的快速Burg 算法的谱分析结果分别如图9(a)和9(b)所示，两种方式都可分辨出15 Hz 和20 Hz 两个谱峰，快速Burg 算法的谱分析结果更为平滑，阶数为7 阶；当输入数据长度为128 时，上述两种算法的谱分析结果分别如图9(c)和9(d)所示，FFT 算法无法得到两个独立谱峰，而自适应定阶的快速Burg 算法依然可以产生15 Hz 和20 Hz 两个独立谱峰，自适应定阶为5 阶。

图9 FFT 算法与自适应定阶快速Burg 算法谱分析结果

综上，自适应定阶的快速Burg 算法在短序列谱分析中具有更高的频率分辨率，在实际应用中，对实时性要求较高时，具有较为重要的意义。

3.2 计算时间

快速Burg 算法与Burg 算法相比，从硬件加速设计上分析，Burg 算法的前后向预测误差ef、eb，反射系数k，AR 参数a，最小预测误差功率Pmin的计算4 组变量完全是串行关系，无法并行化[15]。Burg 算法计算单元在每阶下所消耗的时间如表1 所示。

表1 Burg 算法计算单元消耗时钟数

对于快速Burg 算法，自相关的计算与其他变量无关，只与输入序列和当前阶数相关，它作为耗时最长的运算单元，可以提前一个流水线周期计算。在设计中采用并行的二级流水线结构，并对流水线进行灵活的启动终止控制，使该算法与加速前相比可以将整体计算速度提高约50%。其各个计算单元所消耗的时钟数如表2 所示。

表2 快速Burg 算法计算单元消耗时钟数

最后，本文对两种算法在不同阶数下的硬件实现时计算单元所消耗的时钟数进行比较。以输入数据长度N=128 为例，如表3 所示，快速Burg 算法的硬件加速实现方案确实可以起到更为有效的硬件加速作用，在AR 阶数在10 阶以内时，与Burg算法相比，可将计算时间降低75%。

表3 各算法在不同最终阶数时计算单元消耗时钟数

3.3 内存空间分析

快速Burg 算法的硬件实现方案主要从反射系数k的计算中减少RAM 的使用。其中自相关的计算由于流水线的设计无需存储器进行存储，列向量r 和g 需要进行存储，其存储深度等于阶数，在本设计中阶数在2～10之间，故深度为10，宽度分别为4 B 和6 B。而Burg 算法在计算反射系数k 时，需要为前后向预测误差ef、eb这两个参量分配存储空间，所需RAM 的宽度为2 B，深度和输入数据长度N 有关。因此，快速Burg 算法的硬件实现明显更加节省面积。

3.4 硬件实现资源使用情况

采用如图4 所示的自适应定阶快速Burg 算法的实现方案在Xilinx Virtex7 实验平台上做了仿真测试，综合结果如表4 所示。

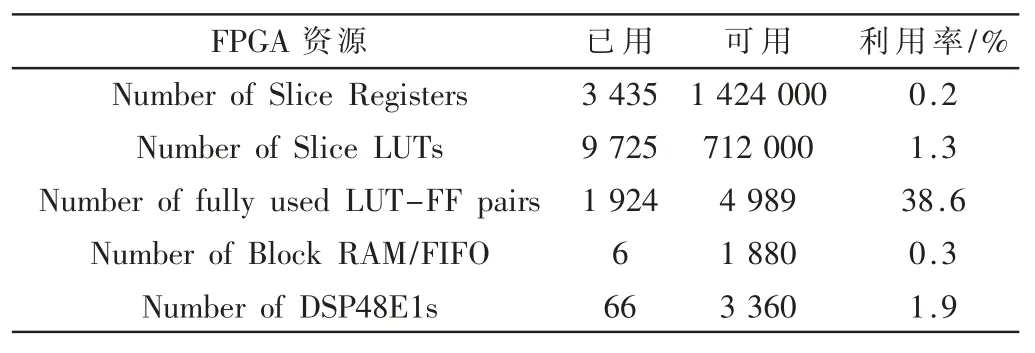
表4 资源使用情况

4 结论

本文以Xilinx 公司的Virtex7 开发板作为硬件平台，完成了自适应定阶的快速Burg 算法设计与实现。提出灵活控制的并行二级流水线结构和并行化计算单元结构，达到了硬件加速的目标。同Burg 算法相比，其对短序列的处理在达到较高分辨率的同时，计算时间可降低75%以上，同时减小了内存空间，并自适应定阶。实验发现，AR 模型阶数是否达到最优决定了功率谱质量的好坏，但是此最优阶数的确定也与输入序列长度、采样率等相关，这一关系有待进一步研究。