平头塔机塔顶结构受力状态与设计方法研究

郭振坤，李 斌

（沈阳建筑大学 机械工程学院，辽宁 沈阳 110168）

近几年所出现的平头式塔机大多数都采用起重臂和平衡臂通联的形式，或通过塔顶架连接起重臂和平衡臂。在起重臂与平衡臂结合部，都要有杆件1 和杆件2 这2 根截面明显大于两侧腹杆的杆件构成一个三角形，作为承受起重臂上弦杆和平衡臂上弦杆拉力差的塔顶架，如图1 所示。

图1 三角形塔顶架

塔顶架可以直接铰接到上转台上，也可以与起重臂或平衡臂构建到一起。无论采用哪种方式，对于起重臂和平衡臂的受力状态都没有影响。但塔顶架顶部的位置对构成塔顶架的杆件本身以及对下部两支点的作用力都有影响。

本文研究这类三角形塔顶架顶部的位置与受力状态的关系，为这类结构设计提供参考。

1 塔顶三角架两根杆件轴力

塔顶三角架2 根杆件轴力如图2 所示。

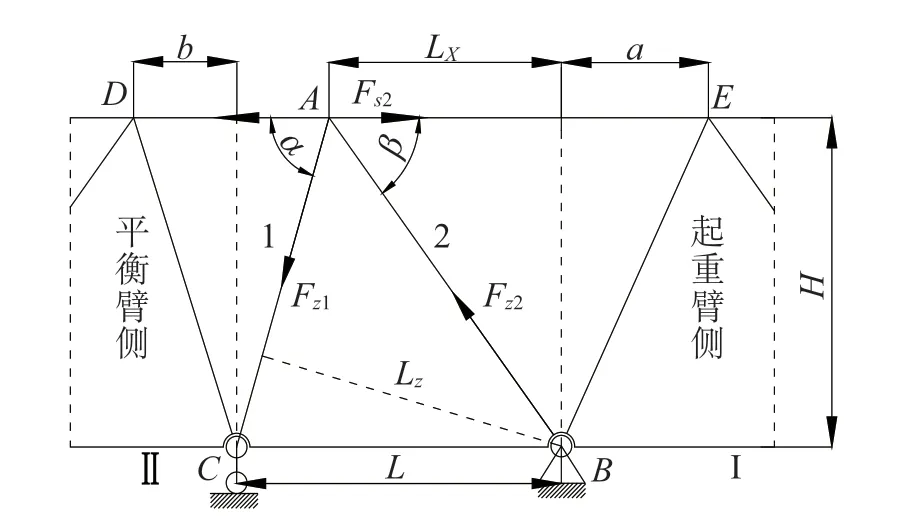
图2 塔顶受力分析图

塔顶架所受的载荷主要是起重臂和平衡臂上弦杆的拉力差ΔF，图2 给出了两上弦杆拉力示意图，则拉力差ΔF=Fs2-Fs1。

Fs1是平衡臂侧上弦杆的最大拉力值，对于任意一台参数固定的塔机基本上都是固定值，ΔF的大小取决于起重臂上弦杆最大拉力Fs2的大小。由于在平衡重的设计中，通常采用最大满载前倾力矩等于空载后倾力矩，实质上是平衡臂一侧的配重与自重所产生的总后倾力矩在平衡了起重臂一侧全部自重载荷产生的前倾力矩的基础上，又平衡了活动载荷产生的最大前倾力矩总量的1/2。由此可得在最大起重量所能达到最大幅度时，ΔF为指向起重臂方向的作用力ΔF1

φ2——起升动载系数；

Pq——吊重、吊钩、小车和钢丝绳所产生的载荷；

R1——活动载荷的工作幅度；

H——三角形塔顶架的计算高度；

L——三角形塔顶架的计算宽度；

Gcg——变幅小车和吊钩自重产生的载荷；

Rmin——变幅小车所能达到的最小幅度；

ΣGpi——平衡臂、配重、起升机构、电气柜自重载荷之和；

ΣGbi——起重臂自重载荷。

在塔机空载状态且起重小车处于最小幅度，吊钩上升到最大高度，则ΔF为指向平衡臂方向的作用力ΔF2

由于动载系数φ2>1，所以有

对于三角形塔顶架而言，其受力如图2 所示，Fz1、Fz2分别为1 号和2 号两杆件的轴力，Lx为B点到塔顶架顶点的水平距离，Lz为B点到1号杆件的垂直距离，由几何关系可得

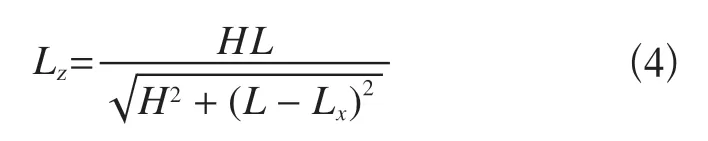
对B点取力矩平衡可得

根据图2 中A点几何关系可得

式中，α—1 号杆与上弦杆所成夹角。

式中，β—2 号杆与上弦杆所成夹角。

由A点竖直方向上力平衡得

图3 是以PTT7020 塔机的塔顶参数绘制的塔顶架两根杆件轴力随着Lx的变化示意图，其中Fz1和Fz2是前倾力矩在三角架两杆件上引起的轴力，F′z1和F′z2是后倾力矩在三角架两杆件上引起的轴力，Lx=0 时，2 号杆件为竖直杆件，1 号杆件为斜杆，属于向前倾的直角三角形。当Lx=L时，1号杆为竖直杆，2 号杆为斜杆，属于后倾的三角形。

图3 三角架两根杆件的轴力变化图

从图3 中可以看出，塔顶架在倾覆力矩作用下，Lx从0～L的变化过程中，杆件1 的轴力逐渐变小，杆件2 的轴力逐渐变大。说明塔顶架顶点的位置影响塔顶三角架杆件的轴力；从图3 中的两组图线可以看出，后倾力矩在塔顶架上产生的轴力都小于前倾力矩在塔顶架上产生的轴力。

2 塔顶架设计方法的研究

2.1 三角形塔顶架截面参数

图3 给出的是塔顶架两根杆件1 和2 在前倾和后倾力矩作用下的受力状态。在前倾力矩作用下，都有杆件1 受拉力Fz1，杆件2 受压力Fz2作用。在空载后倾力矩作用下，杆件1 受压力F′z1，杆件2 受拉力F′z2作用。一般塔机上1 号和2 号杆件的截面参数都是相等的。实际上根据塔顶A点位置的不同，采用等计算应力设计法，1 号杆件的截面参数与2 号杆件的是不相同的。

从图3可以看出无论塔顶A点处于任何位置，前倾力矩作用下两杆件的轴力都大于后倾力矩在两杆件上所产生的轴力。所以在设计上可以采用前倾力矩作用下选择两杆件的截面参数，然后用后倾力矩产生的轴力进行校核。

在前倾力矩作用下，1 号杆件的拉应力σFz1为

式中A1——1 号杆件的截面积。

2 号杆件的计算压应力σFz2为

式中φ2——2 号杆件的稳定系数；

A2——2 号件的截面积；

对于任意给定的Lx，令σFz1=σFz2，则有

式(11)给出的是2 号杆件截面参数相对1 号杆件截面积的比例关系。

当以σFz1=σFz2为设定计算应力值时，两杆件的截面参数就可以成为确定值。

对于后倾力矩的校核计算，可以只计算后倾力矩作用下，1 号杆件受压的计算应力，其计算应力值应满足条件

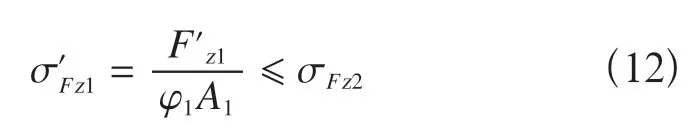
式中φ1——1 号杆件受压稳定系数。

如果所选用的1 号杆件截面参数不能满足式(12)的要求，应调整1 号杆件的截面参数或截面形式，以提高稳定系数φ1。

2.2 三角形塔顶架顶点位置

三角形塔顶架的形式不仅对自身的受力状态有影响，而且还对下部支撑结构的受力状态也有影响。其下部的支点产生的水平力，用以抵抗起重臂或平衡臂下弦杆产生的水平力，以减小其对支座和塔顶架下弦杆的作用力。一般情况下，起重臂下弦杆产生的水平作用力要大于平衡臂下弦杆产生的水平力，在正常情况下都将塔顶架的三角形设计成后倾形式，使2 号杆能产生较大的水平力抵抗起重臂下弦杆的作用力。

图2 中2 号杆件在B点产生的水平力为

根据式(13)，当Lx=L时，F′xz2=ΔF1，这是塔顶架中杆1 竖直、杆2 倾斜的直角三角形状态，也有一些属于三角形塔顶偏向后倾的设计，如使则

3 结语

本文以平头式塔机三角形塔顶架为对象，依据塔机平衡重的计算方法，分析起重臂上弦杆和平衡臂上弦杆力差对三角形塔顶架两根杆件上轴力的影响，研究塔顶架的设计方法，取得了以下成果。

1)建立了起重臂和平衡臂上弦杆轴力差的基本计算方法，并给出了计算表达式。

2）依据两上弦杆轴力差，推导出了三角形塔顶架两根杆件轴力计算的通用表达式。

3）给出了一种塔顶架两根杆件截面参数的设计方法，可以作为塔顶架设计的一种理论依据。

4）分析了塔顶架顶点位置对杆件产生水平力的影响，并给出了塔顶架顶点位置与所产生水平作用力的关系。