双臂并行式特大型平头塔机起重臂弦杆截面设计
2018-08-16李斌,成才,王刚
李 斌,成 才,王 刚
(1. 沈阳建筑大学 机械工程学院,辽宁 沈阳 110168;2. 中建三局集团有限公司,辽宁 沈阳 110000)
特大型平头式塔机起重臂一般都采用倒三角形结构,由于承受很大的弯矩和垂直载荷,采用常规的设计思维可能造成外轮廓尺寸过大,或主肢的截面很大,在保证运输的前提下,结构的外轮廓必将受到限制,只能采用较大的单肢截面面积,造成材料强度的利用率大孤独下降。另外单一的倒三角起重臂,只有1套起升系统,在起重机正常使用状态下,所起吊的都是中小型构件,使得大功率的起升和变幅系统频繁地为起吊中小型构件而运行,造成了能源和机械系统的浪费。
文章研究了一种双臂并行式特大型平头塔机系统,该机采用2个相同倒三角起重臂并行共同承受起重载荷,每个起重臂上有1个起重小车,并对应每个小车安装1套起升机构和变幅机构(如图1所示),这样可以有效解决上述问题。
1 双臂起重机组成
图1为双臂并行式平头塔机的组成,其起重臂由双倒三角形起重臂并联而成,2个起重臂中间上弦杆采用剪力销连接,下弦杆采用水平腹杆连接,2个变幅小车分别安装在2个下弦杆上,如图1中A-A所示。平衡臂上对应安装2套起升机构和变幅机构,2个变幅小车可以同步运行,也有可以单独运行。

图1 平头塔机上部结构图
文章主要研究这种形式的2个起重臂在联合工作时的受力特点,研究起重臂弦杆截面设计方法,为这类起重臂的设计奠定力学基础。
2 载荷与受力分析
2.1 起升平面
起重臂在起升平面可看做长为L的悬臂梁,受到沿起重臂长度分布的起重臂自重载荷和起重小车及吊重产生的集中载荷,一般情况下集中载荷作用在臂端时起重臂处于最不利受力状态。
设起重臂共有n节,第1节与回转节连接,其与回转节连接端为坐标原点,起重臂轴线为x轴,作用在臂端的集中起升载荷为Q,第i节长度为li,其线质量为

式中 c1——线质量系数;
Ali—— 第i节并联起重臂两外侧上弦杆横截面积;
Azi—— 第i节并联起重臂两中间上弦杆横截面积;
Axi—— 第i节并联起重臂两下弦杆横截面积。
图2为起重臂在起升平面的受力状态的力学模型。
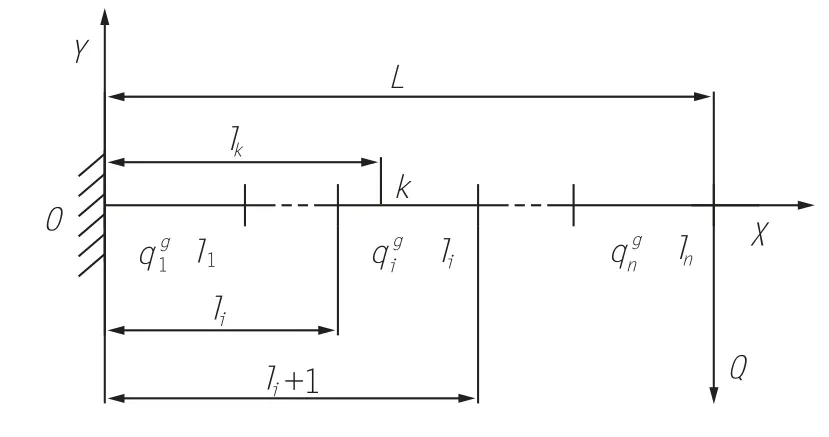
图2 起重臂起升平面力学模型
如图2所示,在起重臂上第i节任取一点k,其与坐标原点的距离为lk,起重臂自重在点k产生的弯矩为
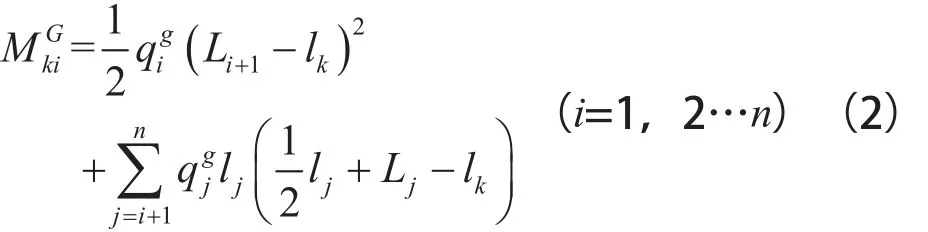
式中

在起升平面内k点弯矩

2.2 回转平面
起重臂在回转平面内受到风载荷和回转惯性载荷,取风载荷与回转惯性载荷同向,一般情况下单节起重臂的迎风面积与其线质量相关,设有常数组C2i满足

C2i——第i节起重臂风载荷系数。
作用在臂端由吊重产生的风载荷为

式中 c3——吊重风载荷系数。
图3为起重臂在回转平面的风载荷的力学模型。
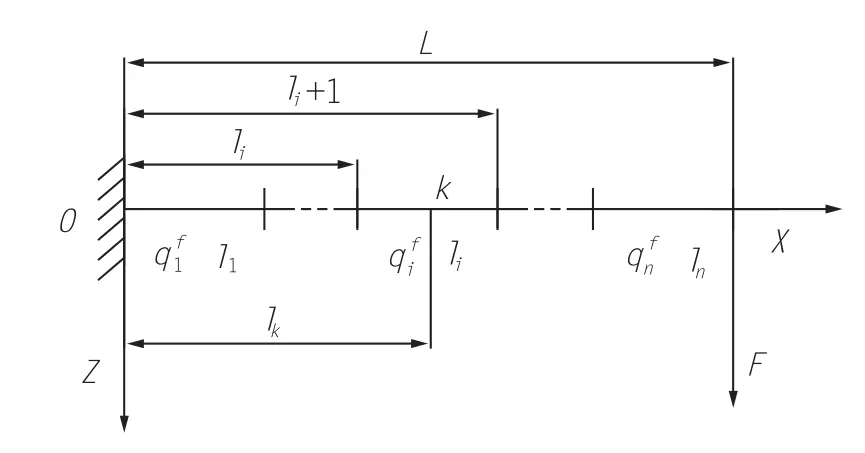
图3 起重臂回转平面风载荷力学模型
起重臂所受风载荷在点k处产生的弯矩为

在回转平面内由风载荷作用在点k处产生的弯矩为

图4为起重臂在回转平面内回转惯性载荷的受力模型,在起重臂上第i节任取一点k,点k处的回转惯性载荷为

式中 Rk——点k处的回转半径,Rk=lk+e;
C4——起重臂回转起制动时的角加速度;
e—— 第一节起重臂与回转节连接铰点到回转中心的距离。

图4 起重臂回转平面惯性载荷力学模型
作用在臂端由吊重产生的回转惯性载荷为

起重臂产生的回转惯性载荷在点k处产生的弯矩为

积分得

式中

在回转平面内由回转惯性载荷作用在k处产生的弯矩为

在回转平面内k的弯矩为

2.3 主弦杆轴力及横截面积
图5中,a为一侧起重臂上弦杆中线距离,z为并联臂2个中间上弦杆的中线距离,b为两外侧上弦杆的中线距离,h为起重臂上下弦杆的中线距离,如图可知b=2a+z,并联臂两下弦杆中线距离为b-a。

图5 并联起重臂截面图
在起升平面内:由于起重臂结构共有4根上弦杆,2根下弦杆,则每根上弦杆的轴力为

每根下弦杆的轴力为

在回转平面内:设两侧上弦杆的轴力为N3i,中间上弦杆的轴力为N5i,下弦杆的轴力为N4i,且起重臂弦杆轴力与其中线距起重臂中线的距离成正比,则有

解方程组(15)、(16)得


式(17)、(18)、(19)中
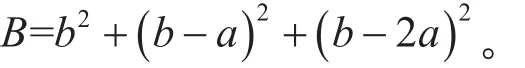
综合起升平面和回转平面,弦杆轴力分别为两侧上弦杆

中间上弦杆

下弦杆
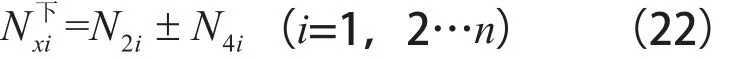
根据式(20)、(21)、(22)可得到中间上弦杆与两侧上弦杆轴力(轴力取较大值)比值为
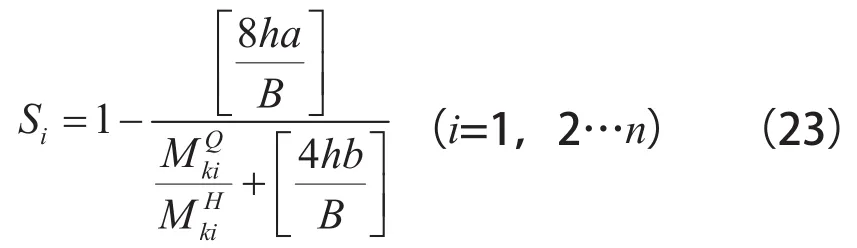
中间2根上弦杆之间的剪力为

考虑起重臂弦杆强度,有


式(25)-(27)中(轴力取较大值):

将表达式(1)-(14),(17)-(22)代入方程组(25)-(27),依次取lk=Ln、Ln-1…L2、L1,可以此解得起重臂各节弦杆横截面积为

将(28)-(30)代入(1)中,得起重臂各节线质量为


表1 式(28)-(31)中字母含义

续表1

表2 表1中字母含义
将式(31)代入式(3)-(12)中,可以得到起重臂在任意长度处的弯矩,进而通过式(20)-(22)可以得到起重臂弦杆任意截面处的各个弦杆轴力;根据式(20)-(22)可知,通过调节并联起重臂截面参数a、b、h,即可调节各节起重臂弦杆横截面积及受力分布状态;根据式(23)可以得到起重臂各节中间上弦杆与两侧上弦杆的横截面积比值和轴力比;根据式(24)可以得到各节起重臂2个中间上弦杆之间形成的剪力。
3 算例分析
在工程实例中,可以取起重臂节数n=7,各节长度li=10m,臂端载荷Q=100000N。当lk=0m,即起重臂臂根处,令z=0.3m、a∈[1,3]m,图6表示在h=1.5,2.0,2.5m 3个不同值时起重臂中间上弦杆与两侧上弦杆的轴力比S随着起重臂截面参数a的变化规律。

图6 轴力比S随a、h的变化图
令h=2.0m、a∈[1,3]m,图7表示在z=0.2,0.3,0.4m 3个不同值时起重臂中间上弦杆与两侧上弦杆的轴力比S随着起重臂截面参数a的变化规律。

图7 轴力比S随a、z的变化图
令a=2.0m、h∈[1,3]m,图8表示在z=0.2,0.3,0.4m 3个不同值时起重臂中间上弦杆与两侧上弦杆的轴力比S随着起重臂截面参数h的变化规律。
从图8、9中可以看出轴力比S随着a的增加而增加,图8、10中可以看出轴力比S随着h的增加而减小,图9、10中可以看出轴力比S随着z的增加而增加。
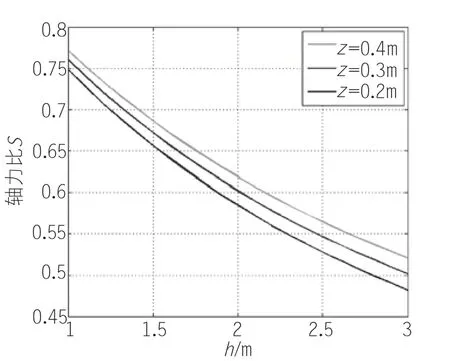
图8 轴力比S随h、z的变化图
取a=2.0m、z=0.3m、h=2.0m时,图9是起重臂弦杆轴力与长度lk的关系图。可以发现,起重臂各个弦杆轴力随着起重臂长度lk的增加而减小,起重臂臂根处轴力最大,臂端处轴力最小趋于零,下弦杆轴力较大,两侧上弦杆轴力差异较大,中间上弦杆差异较小且分布在两侧上弦杆中间。

图9 各个弦杆轴力沿起重臂长度的分布图
图10 是起重臂中间上弦杆与两侧上弦杆轴力比值随起重臂长度变化的关系图,可以发现,在起重臂前3节,比值S下降较快,在起重臂后4节,比值S下降缓慢。
图11是起重臂中间2个上弦杆相互错动形成的剪力,随起重臂长度的增加而减小,在起重臂全长范围内下降平缓。

图10 轴力比S沿起重臂长度的分布图

图11 剪力T沿起重臂长度的分布图
4 结束语
本文利用力学中的悬臂梁模型,求解起重臂任意一处的弯矩,进而求得起重臂在该处的弦杆轴力,得到中间上弦杆与两侧上弦杆的轴力比和2个中间上弦杆的剪力表达式。利用MATLAB绘制相应的关系图,可以看到弦杆轴力相互关系随起重臂截面参数、起重臂长度的变化趋势。在实际工程中,利用这些变化趋势,通过调节起重臂截面参数来调节起重臂的受力分布和设计各个弦杆的横截面积。
