一种高效的阴阳k-Means聚类算法
2021-11-26李长明张红臣李晓光钱超越
李长明, 张红臣, 王 超, 李晓光, 陆 洋, 钱超越
(1. 长春光华学院 工程技术研发中心, 长春 130033; 2. 长春光华学院 电气信息学院, 长春 130033; 3. 长春理工大学 计算机科学技术学院, 长春 130022)
聚类分析是机器学习领域重要的无监督分类方法.k-means聚类算法具有思想简单、收敛性好、易实现等优点, 在矢量量化、图像压缩和空间数据挖掘等领域应用广泛.k-means算法通过不断运行数据分配与中心更新两个步骤优化目标函数值. 在分配步骤中,k-means算法将每个数据点分配给距离其最近的中心, 这需要计算所有数据与所有中心之间的距离, 计算复杂度较高. 针对该问题, 目前已提出了许多加速算法, 其中加速方式分为近似加速和精确加速两种. 在k-means近似加速领域, Wang等[1]使用多个随机投影树建立聚类封闭, 提高了k-means算法在分配步骤中的效率和准确性; Sculley[2]引入了一种小批量采样方法, 该方法可得到更好的收敛效果, 且在处理高维数据集时不会增加计算成本; Hu等[3]提出了一种从粗到细的搜索方法进行多级过滤, 测试数据中比标准k-means算法快约600倍; Fahim等[4]提出了一种距离排除准则, 在连续两次迭代中, 点到中心的距离小于上一次迭代的距离, 则可排除剩余的距离计算, 该准则适用于大型数据集提速; Tsai等[5]利用连续指定次数迭代中不变的划分数据进行加速; Ortegal等[6]通过计算中心的移动概率确定阀值, 排除了距离计算; Ortegal等[7]改进了该算法, 使用等距阈值改善其在大型数据集上的计算效率. 在k-means精确加速领域, Arthur等[8]通过选择具有特定概率的随机起始中心提高算法效率; Zhao等[9]在Hadoop平台上运行k-means算法, 提升了高维数据的聚类效率; Lai等[10]基于距离不等式与相邻迭代之间的移动距离提出了FKMCUCD算法; Pelleg等[11]提出了一种结构优化的方法, 使用k-d树简化最近邻查询步骤, 但当维数大于20时, 该算法的聚类效果不理想; Shu等[12]提出了一种Ballk-means算法, 通过引入球聚类和最近邻聚类的思想创建了一种高效且自适应的k-means算法; 文献[13-14]相继提出了基于三角不等式的算法, 通过减少点到中心距离计算加速k-means算法.
Ding等[15]在文献[13]算法和文献[14]算法之间进行折中, 提出了阴阳k-means算法. 阴阳k-means 算法属于精确k-means加速算法, 具有与k-means算法一致的迭代结果. 其通过中心分组及引入全局过滤器、组过滤器和局部过滤器排除数据与中心之间的距离计算. 与文献[13]算法和文献[14]算法相比, 阴阳k-means算法能继续加速的前提是能在中心分组下整体进行距离排除判定, 与逐个中心判定相比可节约大量判断操作. 但阴阳k-means并未利用数据的结构关系进行加速. 如果直接采用与阴阳k-means中类似的中心分组方法进行数据分组, 由于分组数据的分布半径大于单个数据的分布半径, 整体判定条件相比于单个数据更难满足. 当整体判定失败时, 数据分组将不再具有优势, 因为阴阳k-means算法无法继续进行更细粒度上的整体判定操作. 针对该问题, 本文在阴阳k-means算法的基础上进行改进, 建立满m叉树将数据分组, 以分组后的叶子节点数据建立加权数据进行加权k-means迭代. 由于加权后数据半径与单个数据半径相同, 该方法进行距离排除判定时具有比阴阳k-means整体判定更高的成功概率, 可以进一步提升阴阳k-means算法的计算效率.
1 阴阳k-means算法
阴阳k-means算法通过三角不等式原理计算距离的上下界过滤数据与中心之间的距离计算, 并通过移动距离进行上下界的更新与估计. 设x为数据点,C表示聚类中心的集合,gi⊆C(i=1,2,…,k)为中心集合C的一个分组,b(x)为x的最佳分配聚类中心,d(x,b(x))表示x到最佳中心的距离,d(x,c)表示x到c的距离,b(x,gi)表示gi中x的最佳聚类中心标签,δ(gi)表示每个组的最大移动幅度,lb(x,gi)表示除b(x)外所有中心之间的最短距离. 阴阳k-means算法利用
|d(x,b)-d(b,c)|≤d(x,c)≤d(x,b)+d(b,c)
(1)
进行距离过滤, 其中b,c表示两个不同的聚类中心. 阴阳k-means算法设置三层过滤器进行距离排除操作. 首先, 进行全局过滤, 对于每个点x, 该算法通过保持上限ub(x)≥d(x,b(x))和全局下限lb(x)≤d(x,c)(∀c∈C-b)完成全局过滤. 其次, 以到最近聚类中心的距离作为上界, 到第二近聚类中心的距离作为下界进行组过滤. 该步骤将k个簇分成t个组G={g1,g2,…,gt}, 其中每个gi∈G是一组集群, 将t设为不大于k/10的值. 最后, 将全局过滤条件应用于每个组. 设置局部过滤器, 找到新的b(x), 并利用到第二近中心的距离更新组下限lb(x,gi). 对于被组过滤器阻止的组, 用lb(x,gi)-δ(gi)更新下限lb(x,gi), 用d(x,b(x))更新上限ub(x). 在更新步骤利用中心更新公式更新阴阳k-means算法的中心.
阴阳k-means算法通过中心分组完成gi内所有中心的批量过滤操作, 如果过滤成功会使其比传统的逐个中心判定比对操作计算量更小. 但其并未利用数据结构进行加速. 针对该问题, 本文提出一种加权数据的阴阳k-means聚类算法. 通过数据加权, 既完成了多个数据的统一判定与过滤操作, 同时, 加权数据本身由一个数据点代表多个数据点并未增大数据的半径, 判定条件易满足, 可以完成多个数据的同时判定操作.
2 改进阴阳k-means算法
2.1 基于满m叉树的数据加权聚类
2.1.1 数据加权

图1 数据的分组过程Fig.1 Process of data grouping
本文用一种加权数据的方法提高阴阳k-means算法的速度. 该方法将原始数据集F={f1,f2,…,fM}进行k-means迭代, 建立满m叉树的数据结构. 设树的节点度为m, 深度为h, 则共运行(h-1)层标准k-means算法, 第h层叶子节点的个数为m(h-1)个, 树的叶子节点个数即为加权数据个数, 如图1所示. 本文将最终加权数据个数r设为不大于|F|/10的最大整数.
2.1.2 数据加权聚类
本文设定对树的每个节点进行3次k-means迭代, 得到加权后数据X={x1,x2,…,xr}与加权向量W=(w1,w2,…,wr), 再在更新步骤通过加权中心更新公式
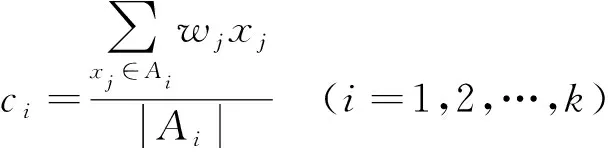
(2)
对加权数据进行阴阳k-means迭代. 其中ci表示加权中心,Ai表示距离中心ci距离最近的所有加权数据点集合.
2.2 中心初始化
本文采用文献[16]的中心初始化方法.
定义1如果对于中心cr, dis(p,cr) 图2 c1和c2是p的有效中心, c3不是p的有效中心Fig.2 c1 and c2 are effetive centers for p, c3 is not an effective center for p 定义2如果中心c不是p的无效最近中心, 则中心c称为数据点p的有效最近中心. 如图2所示,c1和c2是p的有效中心. 虽然c3比c1更靠近p, 但是c2导致c3不满足定义2, 所以c3不是p的有效中心. 有效中心可表示为 (3) 其中dis(p,c)表示下一次迭代中数据点p到中心的距离, UNCp表示点p的最近有效中心集合, average(dis(p,c))表示平均距离, max(dis(p,c))表示最大距离. 根据定义1和定义2为每个数据点建立链表, 在每次迭代期间, 根据式(3)选择一个代入值最大的数据点作为下一个中心, 每次迭代后, 将更新每个数据点的“最近有效中心”链表, 通过此方法降低算法对初始中心的依赖. 1) 利用式(3)初始化聚类中心. 3) 将t设为不大于k/10的值, 并满足内存空间限制. 对初始聚类中心进行5次k-means迭代, 将其分为t个组G={g1,g2,…,gt}. 4) 对所有加权数据运行1次加权k-means算法, 对每个数据x, 设上限为ub(x)=d(x,b(x)), 下限lb(x,gi)为x和Gi中除b(x)外所有中心之间的最短距离(上限和下限分别为距离中心点第一和第二近的距离). 5) 利用式(2)更新中心, 计算每个中心的移动幅度δ(c), 并记录每组的最大移动幅度δ(gi). 7) 设置局部过滤器. 对于每个剩余点x, 利用目前找到的第二近的中心过滤剩余中心, 计算x到过滤中心的距离, 找到新的b(x), 并用到第二近中心距离更新组下限lb(x,gi). 对于未通过过滤器的组, 用lb(x,gi)-δ(gi)更新下限lb(x,gi), 用d(x,b(x))更新ub(x). 8) 重复步骤5)~步骤7), 直到迭代结束. 9) 再对原数据集F进行5次阴阳k-means算法的迭代, 得到最终聚类结果. 本文实验的5组对比数据均来自UCI机器学习数据库, 数据集信息列于表1. 实验环境为Intel I-54200H 2.8 GHz双核处理器, Windows10 64位操作系统, 8 GB内存, VS 2010开发平台. 所有算法均使用C++语言实现. 表1 5组UCI数据集特征 实验分别测试k-means算法、本文算法、传统阴阳k-means算法(阴阳-k)[15]、FKMCUCD算法[10]和Ballk-means (Ball-k)[12]算法的运行情况, 结果列于表2. 以k-means算法的运行速度为基准, 用SKM表示k-means算法的速度,Salgm表示其他聚类算法的速度,HKM表示k-means算法的函数值,Halgm表示其他聚类算法的函数值, 则加速比E和函数值误差百分比I分别表示为 E=SKM/Salgm, (4) I=1-HKM/Halgm. (5) 表2 不同算法在测试数据集上不同聚类个数下的运行结果 图3 4种算法在不同数据集上的平均加速比Fig.3 Average speedup of four algorithms on different data sets 由表2可见, 只有本文算法与传统阴阳k-means算法在所有测试条件下加速比均大于1, 表明这两种算法能在所有测试条件下加速k-means算法, 具有广泛的适用性. 加速算法Ballk-means与FKMCUCD在k值较大时具有较好的加速效果, 对于某些小k值, 加速比略低. 图3为当聚类个数为10,20,30,50时4种算法在UCI数据集上的平均加速比. 由图3可见, 在5组UCI数据集上, 本文算法的平均加速比始终保持最高, 平均加速比最高达59.4, 而其他算法的平均加速比最高为8.35. 本文算法的高加速比是因为本文算法在数据加权聚类过程中, 充分利用了数据的结构信息, 用加权数据代替临近区域内数据点集, 大幅度缩减了距离比对与计算次数. 通过数据加权, 既完成了多个数据的统一判定与过滤操作, 同时, 加权数据本身由一个数据点代表多个数据点并未增大数据的半径, 判定条件易满足, 可以完成多个数据的同时判定操作. 表2的最后一列为本文算法函数值误差百分数. 从数据结果可见, 在多数情况下, 本文算法与传统阴阳k-means聚类(k-means与阴阳k-means算法结果一致)相比, 函数收敛精度基本相同或更高. 唯一一组误差较大的数据为Kegg数据集, 其函数值误差百分数为27.88%~33.22%. 在两组数据Pen-digits与Gas中函数误差始终不超过5.59%, 在LR数据集合上多数结果误差不到10%. 在Page数据集合上具有比传统阴阳k-means算法明显更高的收敛精度, 优化幅度最高达284.26%. 测试精度结果表明, 虽然利用加权数据代表多个数据点降低了聚类的迭代精度, 但利用权向量进行加权阴阳k-means算法迭代在一定程度上克服了数据约简导致的精度损失, 而且基于加权结果采用精确聚类迭代进一步提高了收敛精度. 综上所述, 针对阴阳k-means算法聚类加速过程未利用数据自身相似性, 计算效率较低的问题, 本文提出了一种基于数据多层分解的阴阳k-means加速算法. 该算法根据数据相似性建立满m叉树结构逐层分解数据, 以树结构各叶子节点中存储的数据信息建立加权数据, 运行加权阴阳k-means算法得到收敛中心. 在原始数据中以加权数据收敛中心为初始化条件运行阴阳k-means算法进一步优化目标函数值. 与k-means、传统阴阳k-means以及其他加速算法对比结果表明, 本文算法在不同数据集上始终具有较高的计算效率, 平均加速比最高达59.40, 而其他算法的平均加速比最高为8.35. 此外, 在多数测试条件下函数收敛精度误差不到10%, 与传统阴阳k-means算法精度基本相同.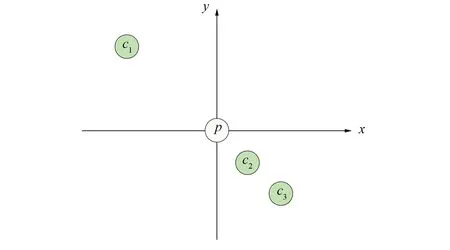
2.3 算法流程

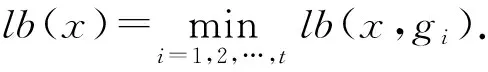
3 实 验
3.1 实验环境与实验数据

3.2 实验结果与分析


