基于用户购买意愿力的协同过滤推荐算法

刘 军, 杨 军, 宋姗姗

(吉林大学 计算机科学与技术学院, 长春 130012)

推荐系统能为用户提供精准、快速的业务(如商品、项目、服务等)信息[1], 不仅有利于用户发现未知的感兴趣商品信息, 而且有利于网站以特色项目快速吸引并发展目标用户群体, 实现用户和网站的互惠.

目前已有的多数推荐系统算法是解决冷启动、稀疏等问题[2], 提高推荐的准确性[3], 而针对目标用户购买意愿的推荐算法相对较少. 文献[4]将价格影响系数和折扣影响系数混合加权到预测评分中, 由于计算中考虑了更细致的影响用户购买因子, 从而有效提升了归一化折损累积增益(NDCG)排序指标, 该算法尽管在购买能力方面有一定效力, 但不是针对购买意愿力及目标用户的算法； 文献[5]提出了一种矩阵分解和K-means聚类的推荐算法, 对用户评分类别中的兴趣点值(POI value)重点加权, 从而提高了推荐的准确率和召回率； 文献[6]提出了一种基于双聚类的协同过滤推荐算法(BCF), 通过BCF算法将在局部项目上具有相似兴趣的用户聚类, 挖掘出用户和项目之间的局部相关模式, 从而在一定程度上提高了推荐精度； 文献[7]通过矩阵分解和多细节层次(LOD)相似度重点解决了数据稀疏及冷启动问题, 提高了推荐精度； 文献[8]通过词嵌入技术, 提出了Prefs2vec算法, 重点突出了词袋间的多样性及特征, 提升了基于存储的协同过滤改进算法.

但上述算法的目标只针对推荐算法精度, 本文提出一种基于用户购买意愿力的推荐算法, 在用户购买意愿较强烈的前提下, 向目标用户准确推荐其感兴趣的商品, 在减少用户导购迷航的同时, 增加用户购物体验的满意度.

1 协同过滤推荐算法和逻辑回归

1.1 协同过滤推荐算法

协同过滤推荐(CF)算法是推荐系统中广泛使用的一种方法, 其在聚类的思想下[9], 利用大数据分析、数据挖掘等技术将大部分看起来无交集的人, 通过某些特定的算法挖掘出兴趣、爱好都较相似的个别群体, 将他们感兴趣的项目组成一个排序列表推荐给兴趣相似的人[10]. 协同过滤算法应用在全球电子商务领域中的业绩较突出, 例如AMAZON搜索引擎, 其网站上约35%的销售额来自其个性化推荐. CF算法主要分为基于存储的方法(Memory_Based)和基于模型的方法(Model_Based). Memory_Based CF是经用户评过分的项目偏好预测可能最感兴趣的未知项目偏好, 分为基于用户的协同过滤(User_Based CF)和基于项目的协同过滤(Item_Based CF)两种算法[11]. 基于模型的方法使用机器学习(如聚类[12]、回归、数据挖掘、关联规则及Bayes技术等)建立用户与商品之间以及用户与用户之间的关系[13], 然后通过优化过程得到模型参数, 建立的数据模型比原始数据集小, 最终根据模型产生合理的推荐.

1.2 基于项目协同过滤推荐算法

实施基于项目协同过滤推荐(IBCF)算法的主要过程: 首先计算项目间的相似度； 其次通过用户_项目评分矩阵和物品的相似度得出预测评分; 最后通过排序法筛选出最感兴趣的项目为用户生成推荐列表[14]. 测量不同矢量间的相似性通常使用矢量之间的“距离”计算. 设项目a与b之间的相似度为sim(a,b)[15], 其度量方法主要有下列3种.

1) 欧氏距离. 由于平方和是线性规则中的重要表达, 因此多数场景下采用欧氏距离相似度, 表示为

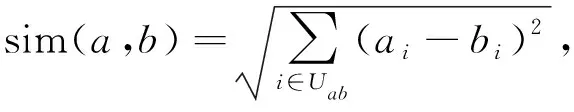
(1)

其中Uab表示对项目a和b评分过的用户集,ai表示用户i对项目a的评分.

2) Pearson相似度. 首先预处理异常值, 然后用数量积计算用户之间的距离. 由于计算相对较复杂, 因此只能应用于带评分的场景, 对不同量纲的评分, 衡量相似度时效果较好, 可表示为

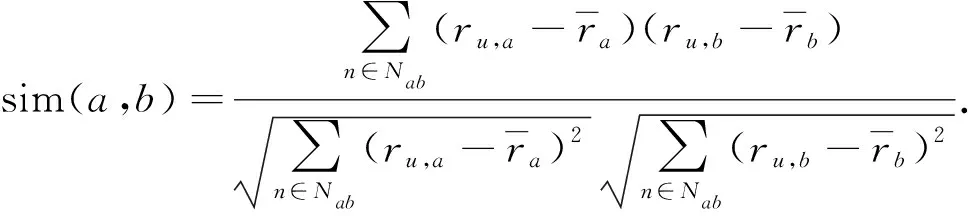
(2)

3) 余弦相似度. 主要用于评分数据稀疏矩阵, 但易受向量平移的影响, 可表示为

(3)

在实际应用中, 需要分析具体问题, 以便采用最适合的相似度计算公式. 本文利用Pearson相似度计算用户或物品间相似度得到的实验效果比其他方法更好[16].

1.3 偏好预测算法

计算项目之间的相似性是以用户对项目的评分为基础, 最终评分预测还可以填充稀疏矩阵, 开放源数据集通常分为培训组和测试组. 传统的评分预测算法如下：

1) 基于用户的邻域算法是关联与目标用户相似性最靠前的用户对物品的预测评分, 构建目标用户的最终评分, 可表示为

(4)

2) 基于物品的邻域算法是在商品间相似度最靠前的物品集合中, 关联兴趣相似用户的预测评分, 构建目标用户的最终评分, 可表示为

(5)

1.4 逻辑回归

逻辑回归(logistic regression, LR)是一种常用的处理二分类问题的线性模型[17]. 本文为解决连续的线性函数不适合分类的问题, 引入非线性函数g:Rd→(0,1)预测类别标签的后验概率:

(6)

这里逻辑函数作为激活函数,x=(x1,x2,…xd,1)T和ω=(ω1,ω2,…ωd,b)T分别为(d+1)维的增广特征向量和增广权重向量.

2 增强矩阵ERM

用表征用户购买意愿力的特征值(浏览Browse、收藏Collect、加购物车Cart)建立购买意愿力评分矩阵Spif. 设商品i在用户购买意愿力评分中的排名为RankScore(即rsi), 将rsi值作归一化、标准化处理后, 代入惩罚因子加权公式, 最后将权重代入增强相似度公式, 得出增强矩阵预测评分.

2.1 标准化

min-max标准化： 以线性方式表示原始数据, 并将数据结果指定在[0,1]内. 对序列x1,x2,…,xn进行线性变换：

(7)

则新序列y1,y2,…,yn∈[0,1]且无量纲.

2.2 惩罚因子算法

协同过滤算法作为推荐系统中的最基本算法, 具有重要的研究价值和应用前景[18]. 基于项目的协同过滤(item-based collaborative filtering, IBCF)作为协同过滤算法的分支之一, 具有优异的性能和较强的可解释性, 已得到广泛应用[19]. 但数据长尾现象是该算法需解决的主要问题之一[20].

文献[21]对基于存储的协同过滤方法进行了改进, 包括缺省投票(根据用户未评分项目的某些规则给出分数)、倒转用户频率(考虑到在一些大众物品上评分相似并不能很好地代表两用户偏好相似, 在小组中给相似项目打分更有参考意义)、放大示例(增强类似的用户权重及减少不同的用户权重), 以此修正物品余弦相似度公式[21], 表示为

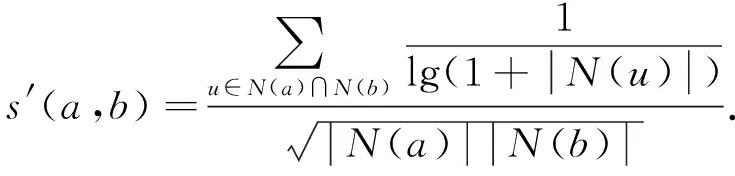
(8)

文献[22]提出了一种基于牛顿冷却定律的热门排序惩罚因子算法, 即将热门排名想象成一个自然冷却的过程. 同理, 在时间流逝中, 客户所关注的项目热度也在不断下降. 因此, 在“时间”和“温度”的基础上构造牛顿渐冷法, 表示为

T=T0e-γ(t-t0).

(9)

之后, 刘欢等[23]进一步改进了该公式, 并将其应用到推荐系统算法中.

本文针对评分矩阵中变量X或Y的线性关系不能清晰体现, 对其进行数据转换后, 得出新的惩罚因子加权公式为

(10)

其中β为惩罚系数, 本文取β=0.5.

2.3 增强矩阵预测评分

设Se为ERM预测评分, 其值为购买意愿力评分矩阵Spif与权值Wpf-i的加权再除以权值总和. 该算法主要针对有购买意愿的商品排名靠后, 从而未被及时推荐导致的长尾效应. 因头部标的物会被越来越多的用户消费, 而质量较好且用户有购买意愿的长尾标的物由于用户关注行为较少, 自身描述信息不足而得不到足够的关注.Se可表示为

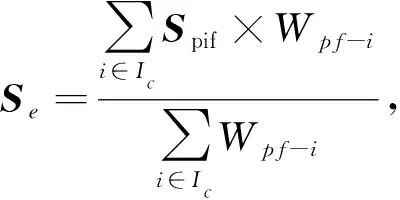
(11)

其中Ic表示购买意愿力较强的用户集合.

2.4 最终评分

设Mui为最终评分, 其值是混合加权基础型评分矩阵BRM与增强型评分矩阵ERM的加权和, 可表示为

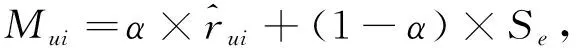
(12)

其中α为调节系数, 本文取α=0.7.

3 实 验

实验采用本文方法与传统IBCF算法在进行对比.

1) 传统IBCF算法. 通过采用余弦相似度计算用户间的相似度值, 得到推荐结果； LRR(logistic regression recommendation)逻辑回归是在推荐算法领域内, 通过设定概率阈值对用户有意购买或无意购买做二值判断；

2) 本文采用增强矩阵协同过滤推荐(ERM-IBCF)算法. 首先, 通过奇异值分解(SVD)降维, 再以Pearson相似度计算用户相似度值, 得到基础型评分矩阵(BRM)； 其次, 用惩罚因子作为增强型矩阵ERM的评价权重, 加权表征用户购买意愿力的商品画像, 取得增强型矩阵ERM的预测评分; 最后, 混合加权BRM&ERM得到最终评分.

3.1 ERM-IBCF算法评价指标

向购买意愿力较强的目标用户推荐TOP-N个下单可能性最大的商品作为兴趣偏好商品, 采用准确率(P)、召回率(R)和综合评价指标(F1)值作为评价标准对推荐性能进行评估, 分别表示为

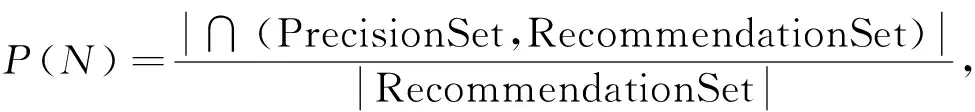
(13)

(14)

(15)

其中: 准确率是通过计算预测偏好与实际偏好相等的数量占整个测试集推荐商品个数的比值衡量推荐的准确度,P(N)表示推荐数量为N时的准确率; 召回率是预测正确的偏好数量占被推荐商品个数的比值,R(N)表示推荐数量为N时的召回率; 综合评价指标F1值越高说明推荐性能越好.

3.2 实验数据集

本文实验数据来源于天池新人挑战赛离线赛, 数据包含约1万个用户的完整行为和位置信息以及近50万条的商品信息, 其中用户行为分类为浏览、收藏、加车、购买, 评分分别为1～4分. 实验中, 将数据划分为训练集和测试集两部分. 通过训练集预测目标用户感兴趣程度最大的兴趣偏好, 再以测试集验证推荐算法的优劣.

3.3 实验结果分析

3.3.1 调节惩罚系数β

选取最优的β值, 得出对应的准确率和召回率.

1) 准确率： 截取区间[0.3,0.6]+0.1内实验数据, 结果如图1所示.

2) 召回率： 截取区间[0.3,0.6]+0.1内实验数据, 结果如图2所示.

图1 不同惩罚因子下的准确率对比结果Fig.1 Comparison results of accuracy under different penalty factors

图2 不同惩罚因子下的召回率对比结果Fig.2 Comparison results of recall rates under different penalty factors

在图1和图2中, 对于每组推荐长度N, 从左至右分别对应β=0.3,0.4,0.5,0.6. 算法ERM-IBCF中, 当惩罚因子β=0.5时, 准确率和召回率的结果达到最优. 随着推荐列表长度的增加, 准确率和召回率的值也增大.

3.3.2 LRR和IBCF与ERM-IBCF算法之间推荐结果对比分析

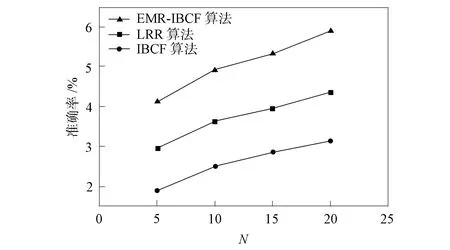
图3 LRR,IBCF和ERM-IBCF算法的准确率对比结果Fig.3 Comparison results of accuracy of LRR, IBCF and ERM-IBCF algorithms

IBCF和ERM-IBCF两种算法分别采用两种不同相似度计算方法, 准确率定义为推荐列表中用户感兴趣且购买意愿较强的商品所占比例, 召回率定义为用户购买意愿较强商品被推荐的概率. 选择准确率和召回率作为实验的基础评价指标,F1值作为实验的综合评价指标, 偏好推荐列表的长度分别取5,10,15,20.

逻辑回归和两种基于用户协同过滤偏好推荐算法在淘宝用户数据集上的推荐准确率、召回率和F1值结果分别如图3～图5所示. 由图3～图5可见: 由于ERM-IBCF算法融合了表征用户购买意愿的评分矩阵, 对购买意愿较强烈的项目进行重点推荐, 因此, ERM-IBCF算法具有更好的重点项目推荐性能; LRR由于包含了较多的目标意愿用户, 所以准确率和召回率略高于IBCF算法, 但与ERM-IBCF算法相比, 后者由于融合了增强矩阵, 重点推荐购买意愿较强项目, 因此ERM-IBCF算法的准确率和召回率高于LRR. 由图3和图4可见, 随着推荐项目数量的增加, 准确率和召回率的增加也非常明显, 这主要是因为目标用户购买意愿较强项目被推荐的数目也在逐渐增多, 从而也逐渐提高了F1值.

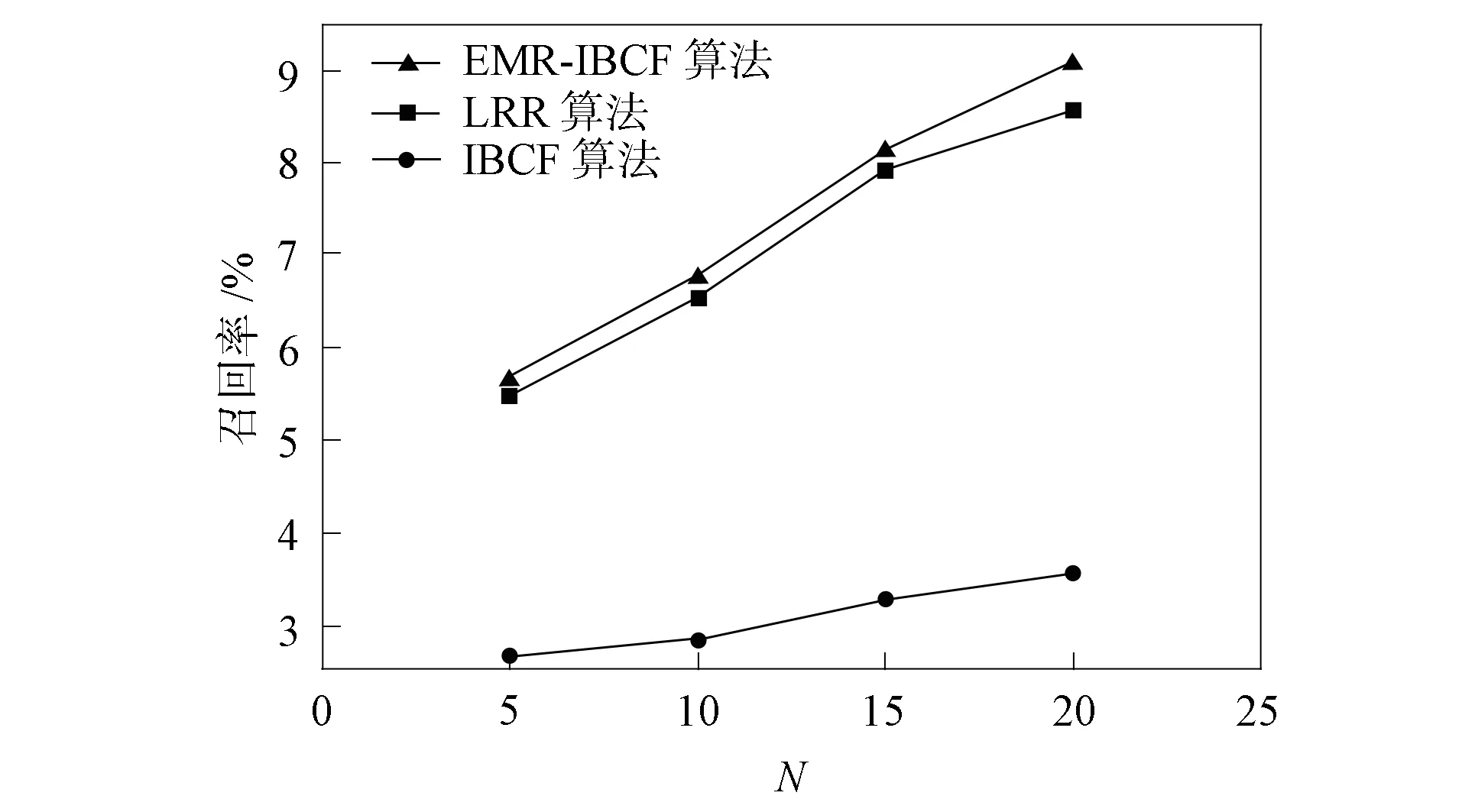
图4 LRR,IBCF和ERM-IBCF算法的召回率对比结果Fig.4 Comparison results of recall rates of LRR, IBCF and ERM-IBCF algorithms

图5 LRR,IBCF和ERM-IBCF算法的F1值对比结果Fig.5 Comparison results of F1 values of LRR, IBCF and ERM-IBCF algorithms

综上所述, 本文针对网购行为中商品浏览量排名靠前而销量滞后的问题, 在用户购买意愿力的基础上, 提出一种增强评分矩阵协同过滤推荐算法. 通过惩罚因子权重算法, 有效解决了兴趣偏移导致的不确定性和因时间等因素导致的感兴趣商品关注热度下降问题; 同时通过对数转换呈现了用户购买意愿力评分排名与惩罚因子权值的线性关系； 通过融合增强矩阵中表征用户购买意愿的评分矩阵, 将用户感兴趣且购买意愿较强的项目从众多下单盲区中, 对目标用户重点推荐, 从而增加用户下单的几率.