浅议微积分学中的“化”

苏 志 勇张 飞 羽

（1.兰州大学数学与统计学院，甘肃 兰州 730000；2.河西学院数学与统计学院，甘肃 张掖 734000）

在微积分学课程的学习中，学生对定理的理解程度，对知识的运用能力，体现在具体的解题过程中.培养学生具有正确得当的解题思路，是教学过程中的重要一环，是对目标教学与结构教学是否有机结合的一种检验.这里所要谈的“化”，是数学中的一种分析和解决问题的重要方法.在此，如果我们把已知的事实、假设、定理、公式称之为“标准型”，把待论证或计算的问题称之为“非标准型”，那么贯穿整个微积分学的思想之一，就是化非标准型为标准型来解决问题（这也是其它数学学科常用的方法）.课程教学中常用的方法有两类，一是恒等变形，在这里也仅仅是分项组合、加减或乘除同一数（式）；另一个就是变量替换.这里的变量替换手段包括RMI原则，即关系映射反演原则，其含义是：假设我们遇到的问题为原像关系结构R，R中原像目标为Z，并且R在中难以解决，为此我们寻找一种可定映射ϕ，将问题R转化成R∗，R∗中映像目标为Z∗，并且能够通过确定的数学方法解出Z∗，然后再通过反演ϕ-1，将原像求解出来.基于此，文中精选了较为充分的例题，除了体现函数的分析性质之间转化具体形式（恒等变形和变量替换）外，还考虑了建构模式转化问题（譬如：微积分学中理论构造性的证明，数学模型的构建，等等）.同时，所选的典型例题都能体现化归思想在分析中的应用.

1 极限理论中的化

这方面的问题有两类，一是直接论证或计算极限A，另一类是给定极限A，求极限B.前者所用依据有：极限的定义、两个重要极限、等价无穷小、夹挤定理、单调有界原理、柯西收敛准则、洛必达法则等等.当然，微积分几乎所有的概念和定义都是由极限定义的，它们反过来也可用于极限讨论；对后者，一般方法是：将B或B的部分形式化成A（或A的拓展形式）来求解.与此相反的作法就是利用f(x)=A⇔f(x)=A+α,将其代入极限B中讨论.当然，对上述两类问题，变量替换法也常常或显或隐地在使用.

1.1 直接论证

提示 通过有理化方法，把其中的极限为零的因子n4+1-n4化去，使之变为常见的形式.

1.2 已知极限A,求极限B

方法2

2 利用函数构造进行转化

在函数的连续性理论和可微理论中，函数构造法比较普遍.例如，用零点定理证明介值定理，以及用洛尔定理证明拉格朗日中值定理和柯西中值定理等.

例4f(x)∈C[a,b],f(a)b⇒∃ξ∈(a,b) ,f(ξ)=ξ.

提示 令g(x)=f(x)-x⇒g(a)∙g(b)<0.

3 利用互逆关系进行转化

常用的互逆关系有：函数与反函数、微分与不定积分、方程（组）与其决定的隐函数（组）、函数展成幂级数与求幂级数的和函数等.例如，等式两边取对数法；利用函数的导数与不定积分计算其反函数的导数与不定积分，如

隐函数存在定理在求曲线的切线方程、曲面的切平面方程、化条件极值为无条件极值等方面扮演着重要角色，如拉格朗日数乘法公式的建立.

例8 求曲面x=x(u,v),y=y(u,v),z=z(u,v)在点M处的法向量.

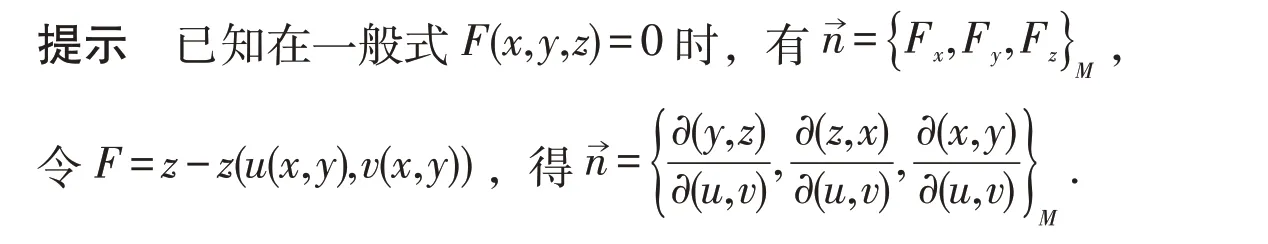
4 利用一些“桥梁”性定理进行转化

（1）利用海因定理，将数列极限的理论用于一般函数，反之亦然，如洛必达法则用于数列极限的计算；

（2）利用微分中值定理及泰勒公式，将函数的性质及特征转化成其导数或高阶导数的性质，反过来研究函数，如函数的单调性、凸性、极值、切线斜率、曲率、近似计算、零点个数估计等；

（3）利用积分理论中的格林公式、高斯公式、斯托克斯公式，进行不同类型积分之间的转化；

（4）利用对无穷区间的分化，进行级数与广义积分之间的转化，如

5 利用函数的局部属性与整体属性进行转化

有限覆盖定理和区间套定理就是局部性质与整体性质之间进行转化的桥梁，如用有限覆盖定理证明连续函数在闭区间上有界，以及用区间套定理证明零点定理.有时在邻域内选取小闭区间也可达到此目的，如幂级数分析性质的论证.另外，最值点即有整体属性又有局部属性，所以它在一些问题的论述中扮演着重要角色，如洛尔定理的证明，一些不等式的证明等.

6 利用常量与变量的辩证关系进行转化

将常量关系转化成变量关系，这一方法在数项级数求和、一些椭圆积分的计算、柯西-施瓦兹不等式的证明等问题中比较常见（如例5）.反之，在局部视变量为常量，以及利用累次法、折线法、固定变量法进行一元函数与多元函数之间的转换，就是将变量关系转化成常量关系很好的例子.

提示 这是关于定点(x0,y0)与其附近点(x0+h,y0+k)的局部问题，在两点连线上构造一元函数ϕ(t)=f(x0+ht,y0+kt)，给出其马克劳林展式后代入

例12 设f(x),g(x)∈R[ ]

a,b，证明施瓦兹不等式

7 利用极限将无限（界）形式转化成有限（界）形式

一般在“有限”情况下，许多性质、运算都成立，如四则运算、两种运算次序的交换等.而微积分的主要内容都体现“无限”，为此，我们常常化“无限”为“有限”加极限，如无穷级数与广义积分分析性质的论证.另外，值得一提的是，有限覆盖定理的应用，它利用命题中每一点的局部性质构造出开邻域簇，再将“无限”问题转化为“有限”问题来处理，如利用有限覆盖定理证明连续函数在闭区间上有界.

提示 两种积分次序的交换可在区间有限的情况下进行.∀A>a，考虑

再利用一致收敛性即可.