制动盘自由模态仿真分析与试验研究

2021-11-26吴心杰杨明付道琪高若奇

农业装备与车辆工程 2021年11期

吴心杰,杨明,付道琪,高若奇

（200093 上海市上海理工大学机械工程学院）

0 引言

相比于鼓式制动器，盘式制动器制动迅速、便于维修，在汽车、机械领域应用广泛[1-2]。盘式制动器主要由制动盘、制动钳、摩擦片等组成，制动过程中，活塞推动制动卡钳使摩擦片与制动盘相接触并发生剧烈摩擦，制动盘急剧升温，把大部分动能转换为热能耗散至空气中，使汽车减速，直至停止。当制动盘固有频率与制动器其他零件固有频率相近或相同时，会发生共振，不仅会影响系统制动性能和乘坐舒适性，更有可能会影响制动器结构稳定性。因此，为避免在行驶过程中使制动盘工作频率落入自身固有频率范围引起共振，有必要对制动盘进行模态分析。

学者对盘式制动器制动性能、振动特性及制动噪声等方面做了大量研究。彭龙[3]等为了抑制盘式制动器制动过程中的噪声，采用区间概率混合模型，对盘式制动器系统进行了稳健优化设计，为盘式制动器系统的结构优化设计提供了有效方法；徐焱[4]等针对某型悬挂式单轨车辆制动噪声问题，建立了制动器有限元模型，并进行了自由模态和约束模态下的有限元分析，得到各零部件的前8 阶固有频率，分析了零部件的振动特性；王文竹[5]等针对某SUV 后轮盘式制动器的制动尖叫问题，通过有限元模型仿真和试验相结合的手段，验证了有限元模型的有效性，且应用复模态分析方法预测出系统的不稳定模态；Kharate[6]等基于有限元法建立了盘式制动器各零部件的模型，探讨了各零部件在不同材料参数下制动盘的制动噪声特性,并通过试验对制动盘模态进行了分析验证；Hu Shugen[7]等基于Stribeck 模型建立了盘式制动器七自由度动力学模型，研究了制动盘在工作过程中的复模态稳定性。

以上研究在盘式制动器模态分析及噪声抑制方面均取得了一定研究成果。本文利用有限元仿真分析和试验的方法对制动盘自由模态进行分析。通过结果比对分析，验证了模型的准确性。

1 模态分析理论

一个具有N 个自由度的线性振动系统，若不计及阻尼的影响，其自由振动的运动微分方程的一般形式可以表示为

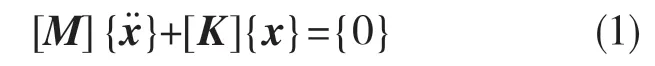
式中：[M]，[K]——质量矩阵、刚度矩阵；{x··}，{x}——节点的加速度矢量、位移矢量。

设方程的解具有简谐运动形式，即

其中，{x}的元素代表各点振幅，代入式（1）得

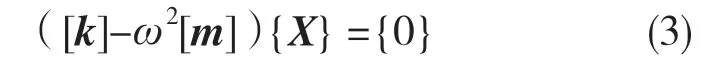
式（3）具有非零解的唯一条件是[Z]=[k]-ω2[m]的行列式等于零，即

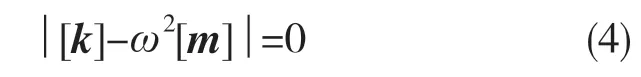
当[m]和[k]皆为正定矩阵时，将式（4）展开后，可得N 个特征值ωr2（r=1，2，…，N），且

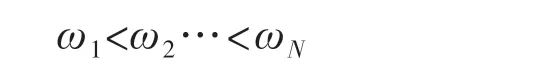
分别称其为1 阶、2 阶、…、N 阶固有频率。

每个特征值均对应一个特征向量{Φ}r，它满足

2 制动盘有限元模型建立

通过对录制的宏代码进行精简化处理，删除不必要的代码之后，在ABAQUS 中快速建立制动盘有限元模型。对模型进行简化处理，但对制动盘帽部的结构细节予以保留，模型建立完毕后的网格划分、定义材料等操作也基于录制宏完成。理论上来说，划分的网格数量越多、尺寸越小，最终计算结果就越可靠，但过于精细的网格划分会带来巨大的计算成本。本模型采用二阶四面体网格划分，相比一阶四面体精度更高，网格类型采用C3D4 类型。制动盘模型网格划分完毕后，共有184 838 个单元，节点数为40 562 个。图1为制动盘实物及其有限元模型。

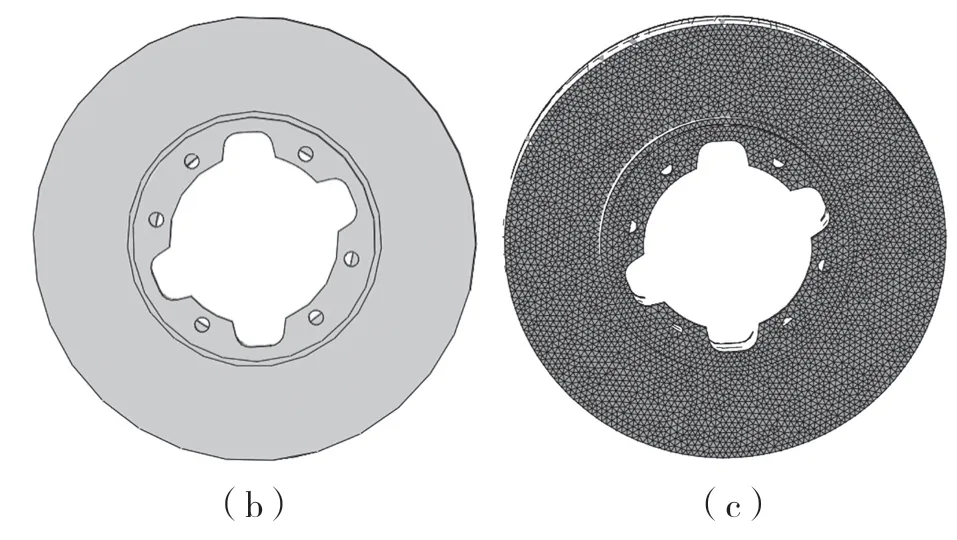
图1 制动盘模型Fig.1 Brake disc model

有限元模型建立完毕后，先定义材料，后划分网格，制动盘材料为HT250—GB9439，相关材料属性如表1 所示。ABAQUS 并没有固定的单位制，只需统一单位制即可，单位制不统一的情况下，仿真是没有任何意义的，本文统一采用SI（mm）单位制。

表1 制动盘材料属性Tab.1 Property of brake disc

3 制动盘模态分析

前处理完成之后，设置Block Lanczos 算法，设定特征值个数为30 以扩大可选范围，因前6阶为刚体模态，频率极低，可以忽略，在分析结果中自第7 阶开始取前6 阶模态。制动盘这种结构存在较多的重根模态，因此采用节圆—节径（m，n）的方法进行描述，节圆表示在某一个圆上各点位移为零，节径表示在某一条直径上各点位移为零，制动盘前6 阶模态频率及其振型描述如表2 所示。

表2 制动盘前6 阶振型及固有频率Tab.2 The first sixth vibration mode and natural frequencies of brake disc

图2 中，制动盘的1、2 阶模态用节圆—节径的方式可分别表述为（0，2）和（0，3），都是只拥有节径的模态，1 阶模态两条节径之间相差π/2，制动盘的变形主要集中在制动盘面上，使得整个制动盘面弯曲成马鞍面形状；2 阶模态每条节径之间相差π/3，制动盘面呈一种波浪状变形，且变形区域主要集中在制动盘面上；3 阶模态下制动盘呈波峰—波谷状变形；4 阶模态下制动盘的变形状况与1、2 阶类似，可表述为（0，4），变形区域主要集中在制动盘面上；制动盘的5 阶模态可视为两个间隔π/2 的（1，1）模态叠加而成；6 阶模态下制动盘的变形与1、2、4 阶模态类似，只是节径数目进一步增多至5 条。通过分析前6阶模态可知，制动盘的变形主要集中在盘面区域，表现为面外模态，工作过程中易于和其他制动系零件产生共振，而且从制动盘前6 阶模态的振动规律可以理论推测存在振型为（0，6）的高阶模态，而仿真及试验也说明了8 阶模态振型确为（0，6），鉴于篇幅所限，不再详述。

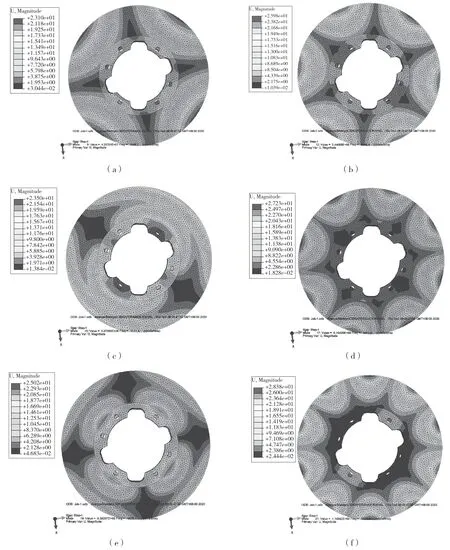
图2 制动盘1～6 阶固有振型图Fig.2 The first to sixth vibration mode of brake disc

必须说明的是，由于设定特征值个数较多，对于一些仿真得到频率相近的模态，应结合其具体振型判断到底是一个过渡状态还是一个稳定的模态，可通过模态振型判断某一阶频率下的模态是否为过渡模态。过渡模态的振型一般毫无规则，不具有分析及实践价值，且过渡模态对应频率与稳定模态比较接近，因此极易发生突变进而转换至稳定模态，应予省略[8]。如在本次仿真的结果中，各阶稳定模态相应频率附近均存在1～2 种过渡状态，应结合相应模态分析理论取最为稳定的一种。

4 自由模态试验

4.1 试验系统组成

试验系统由3 部分组成，一是试验激振系统，为带力传感器的钢头力锤；二是响应拾振系统，包括加速度传感器及COINV 信号采集分析仪；三是模态分析和处理系统，为东方所数据采集及其后处理软件DASP.v10。测试系统组成如图3所示，测试系统现场布置如图4。

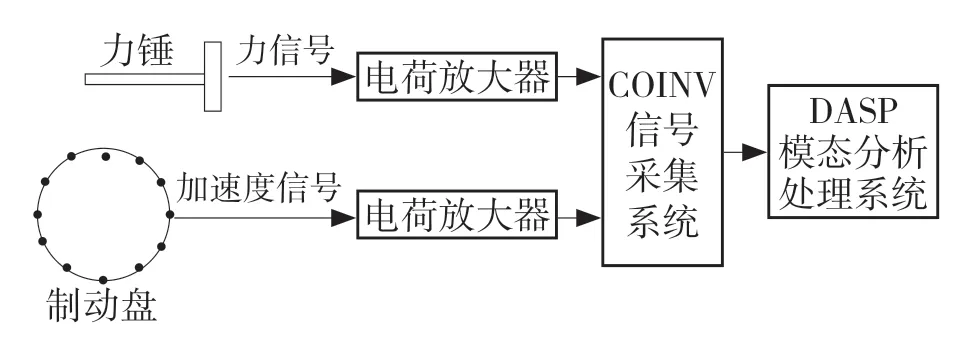
图3 测试系统组成Fig.3 Composite of testing system

图4 测试系统现场Fig.4 Testing system site

试验中用到的仪器、软件信息如表3 所示。

表3 试验仪器参数Tab.3 Test devices’ parameters

4.2 试验方法

试验前将传感器、力锤、电荷放大器、信号采集分析仪及计算机连接好，调试运行并检测信号质量，尽可能避免外界电磁干扰及仪器设备接触不良带来的影响。将制动盘置于双层海绵垫上，因制动盘结构特征在制动盘面与制动盘帽部相结合处发生突变，试验前先在制动盘上根据其结构特征分别在制动盘面的内、外圆周及制动盘帽部内、外圆周上将各个圆周16 等分，并对各点位一一编号，共计64 个点位，取制动盘面外圆上的一号点作为参考点。激励点位分布如图5 所示。

图5 激励点位分布图Fig.5 Excitation nodes distribution

为提取制动盘的面外模态参数，采用单点激振单点拾振试验（SISO）方法，拾振传感器布置方案为在制动盘面最外侧圆周1 号点上布置一个单轴加速度传感器，试验中采用钢头力锤进行脉冲激振[9]，采集信号频率有效带宽为25 600 Hz，信号平均采集次数为3 次，共需激振192 次。

每次采集过程中都实时地进行信号质量的检查：（1）力锤信号有无“连击”；（2）设定预触发延滞，观察锤击力谱在关心频带内是否相对平坦；（3）因加速度信号受高频信号影响较为显著，且钢头力锤激励信号频率较高，需注意加速度信号有无超量；（4）频响函数有无毛刺；（5）信号相干性是否符合要求，除去节点或反共振点外，相干系数在0.75 以上，避免外界噪声输入对试验的影响，以确保响应是由激励引起。模态试验所得制动盘频响函数如图6 所示。

图6 制动盘模态试验频响函数Fig.6 Frequency-response function of brake disc

根据频响函数可大致推断各阶模态所处频率范围，但远远不够精确。从频响函数图线中各个尖峰处取频率片段，经特征系统实现算法（ERA）处理，得到如表4 所示的制动盘的前6 阶模态参数。

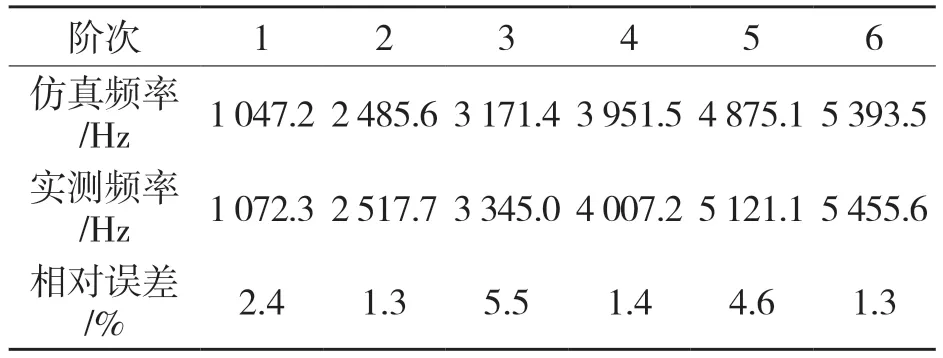
表4 试验与仿真结果Tab.4 Test and simulation results

本次试验误差原因主要由以下几方面构成：一是因为采用“锤击法”测模态数据，人为操作带来的影响无法计算，包括测试系统本身也存在误差；二是制动盘本身材料数据并不一定与仿真完全相同，可能有微小变化；三是在仿真时为了节约计算成本忽略了不必要的结构细节如倒角、螺纹等而引起的计算误差。数据采集过程中对同一测点进行3 次采集取平均以减小误差，且仿真和试验所处测试情况并不相同，结果自然也不尽相同。本次仿真和试验的数据误差平均未超过5%，最小误差为1.3%，在可以接受的精度范围之内。