改进人工蜂群算法在谐振子参数优化中的应用

黄 帅，柳 凯，党建军，张培新

（中国航天科技集团 第十六研究所，西安710100）

半球谐振陀螺（hemispherical resonator gyro，HRG）是一种基于哥式效应工作的谐振式惯性敏感器件，其工作原理是利用谐振子径向振动产生的驻波沿周向的进动来敏感载体旋转[1-2]。相较于传统机械陀螺，HRG 用谐振子来替代机械陀螺转动部件，大大提高了其可靠性及工作寿命。在国外，HRG 已经作为产品广泛应用于航海、航天、航空、战术武器、地面车辆等领域，被称为高价值空间任务优选传感器[3-6]。石英谐振子作为HRG 的核心部件，国外对其进行严格的技术封锁，仅谐振子直径参数有相关报道，而锚杆直径、锚杆长度、球壳厚度等都没有相关资料，因此对谐振子结构参数进行优化设计成为半球谐振陀螺技术研究的重点之一[7-12]。

改进人工蜂群算法（improved artificial bee colony，IABC）是一种新型群智能算法，与人工蜂群算法[13-14]相比，通过将趋势外推计算原理与微调算子引入人工蜂群算法，对其搜索的随机性进行引导，有效地解决了原算法在后期容易陷入局部最优解及后期搜索速度慢的缺陷[15]。本文首先对谐振子进行了参数化建模，并构建出优化模型，将IABC 算法应用于该优化问题，求得目标函数的极值，并对最终优化方案进行仿真。

1 模型优化与模型建立

半球谐振陀螺技术发展历程中，使用过很多不同形状和材料的半球谐振子，目前公认Ψ 形的石英半球谐振子是结构最佳形式，具体结构如图1 和图2 所示。

图1 谐振子结构图Fig.1 Structure diagram of resonator

图2 谐振子参数化示意图Fig.2 Parametric diagram of resonator

1）设计变量：半球壳半径R、锚杆直径D、锚杆长度L、锚杆距唇沿距离l、外圆角值r1、内圆角值r2、球壳厚度H。

根据美国和俄罗斯相关资料，经典谐振子直径为30 mm，其余参数结合谐振子加工特性，设置取值范围如表1 所示。

表1 谐振子设计变量取值范围Tab.1 Range of resonator design variables

2）约束条件：工作状态下，谐振子处于高频振动中，因此要求谐振子满足一定的力学性能。半球谐振陀螺激励包括参数激励与单点激励，其中单点激励是为了实现陀螺起振；参数激励是用于维持谐振子振幅稳定，其伴随陀螺整个工作过程。为了简化模型暂不考虑单点激励，只进行参数激励下谐振子力学性能分析。参数激励是借助环绕谐振子边缘的环形电极实现的，其与谐振子外表面形成电容的两个极板，利用静电力进行激励。根据典型参数，电压V=200 V，工作间隙d=0.1 mm，作用面积S=2 mm2，介电常数ε0＝8.85×10-12F/m，可计算作用在谐振子上的压强约为1.2 MPa。加载上述力学条件进行静力学分析，定义最大拉伸应力S1及最大压缩应力S2作为约束条件；其中最大拉伸应力S1在0～2 MPa 之间；最大压缩应力S2在0～2 MPa 之间。

其次随着设计参数的变化，谐振子低阶的几个振型频率会有交叉耦合，这对谐振子来说是有害振动；为了减小谐振子的模态耦合，应保证谐振子二阶工作频率f2远高于一阶频率f1。

3）目标函数：以重量最轻为优化目标，所以将谐振子总质量M 设为目标函数。对上述模型公式化后，得到30 mm 谐振子设计优化数学模型：

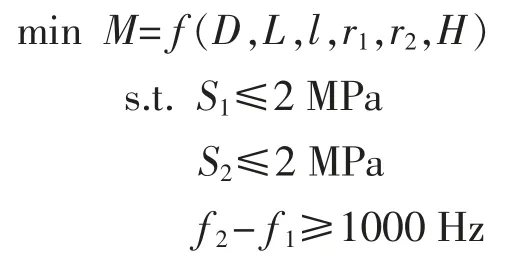
2 改进人工蜂群算法

人工蜂群算法（ABC）是模拟蜂群群体采蜜过程的一种新型群智能算法。蜜蜂是一种群居生物，能够在极其复杂的环境下以较高的效率采集花蜜。研究表明，蜂群采蜜过程中，蜜蜂按任务角色分为3种类型，侦察蜂、引领蜂、跟随蜂，它们通过摇摆舞、气味等多种方式进行信息交流，协同配合完成采蜜。

对于n 维多变量求最小值优化问题：

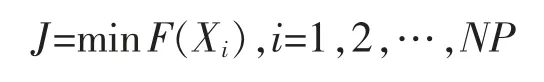
在人工蜂群算法中，首先生成含有NP 个解（食物源）的初始种群，每个解Xi（i=1，2，…，NP）是一个D 维的向量，引领蜂和跟随蜂按照下式进行食物源位置更新：

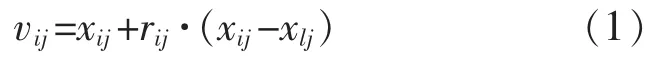
式中：i，l∈NP；j∈D；l≠i；rij∈［-1，1］是一个随机数。

将趋势外推原理应用到人工蜂群算法，利用食物源在不同位置适应度值的大小差异来引导外推方向，可以起到搜索引导作用，能够克服算法本身的随机性。由人工蜂群算法中的食物源位置更新公式（1），再随机产生另外一个虚拟的食物源：

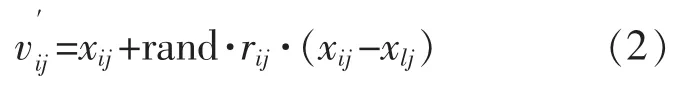
根据外推原理，结合式（1）和式（2）可得：

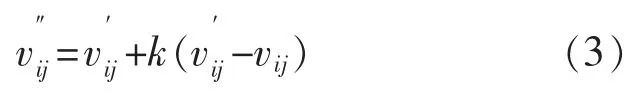
化简式（3）：

式（4）本身具有一定的自适应特性，一般而言，在算法的开始阶段，蜜源比较分散，距最优解较远，蜜源之间的差异较大，用式（4）产生的调节幅度也大；而在算法收敛后期，种群中的优质食物源逐步靠近，参变量差异较小，调节幅度也小，有利于得到精度更高的参量。

但是，在采用式（4）进行食物源位置更新时，很有可能由于参加位置更新的两个解向量的某些参数相近或者相等，使即解的位置无法更新，搜索不能继续进行。为此在式（4）中引入一个微调算子略大于0），即：

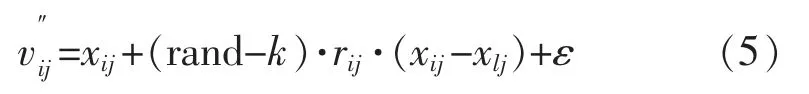
由于微调算子很小，只有xij和xlj非常接近时才会对产生作用，这是一种简单的调节，但微调算子可提高算法后期搜索速度和效率。

IABC 算法中，引领蜂和跟随蜂按照式（5）进行食物源位置更新，跟随概率Pi按照下式确定：

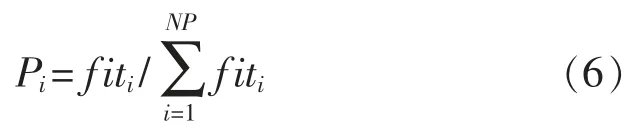
式中：fiti是第i 个解的适应度值；NP 是解的个数。

IABC 算法流程如图3 所示。

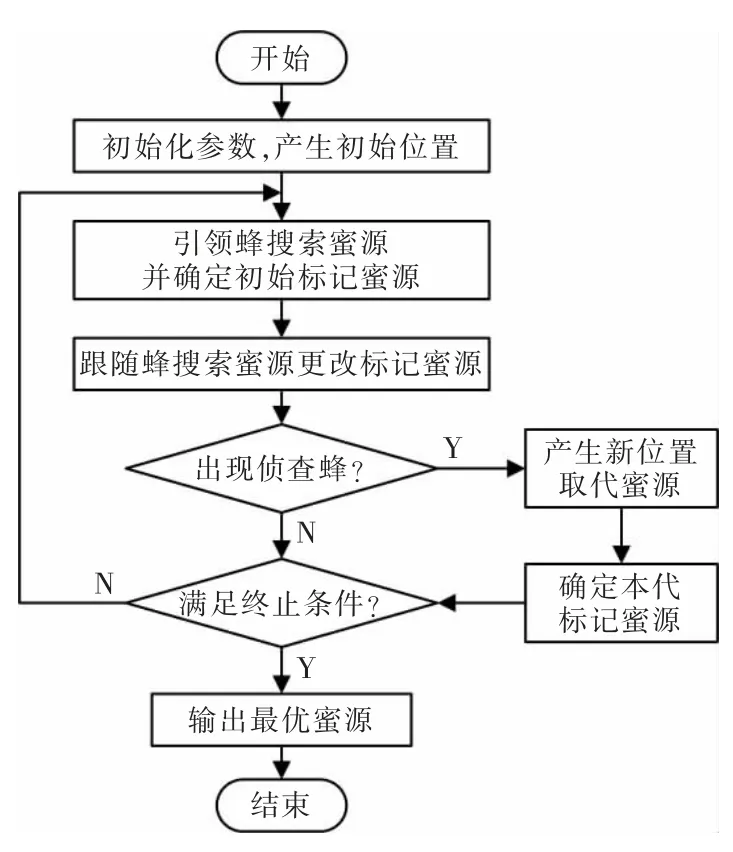
图3 IABC 算法流程Fig.3 IABC algorithm flow chart

3 IABC 算法求解谐振子优化设计问题

IABC 算法可以用来直接求解复杂的无约束非线性优化问题，而谐振子优化问题是带有复杂约束条件的，所以必须采用约束处理方法将有约束的优化问题转化为无约束的优化问题，一般的做法是采用惩罚函数法，即通过给目标函数增加惩罚项。

3.1 优化流程及初始参数设置

IABC 算法求解谐振子优化问题的基本流程如下：

1）确定设计参数个数n 及取值范围；

2）在整个设计空间内进行优化拉丁超立方采样，采样个数为10n 个；

3）通过简单UG 软件及ANSYS 软件二次开发进行各样本点目标函数仿真计算，并将结果输出；

4）通过Matlab 编程实现目标函数结果的读取，并完成IABC 算法寻优；

5）输出满足要求的优化值，结束。

根据前面谐振子几何建模确定的设计变量的范围，利用Isight 软件的DOE 模块采用优化拉丁超立方（OLHD）方法确定NP 个初始解（NP=60），设置IABC 算法中最大搜索次数limit=500，迭代次数Maxcycle=1000。

3.2 谐振子优化结果

经过IABC 算法优化设计后，满足约束条件的谐振子最优设计参数如表2 所示，优化结果对比如表3 所示。目前工程应用方案谐振子重量为6.36 g，经过IABC 算法优化后的谐振子重量约为6.03 g，质量减小了4.9%左右。谐振子最大拉伸应力及最大压缩应力均有所下降，分别为16.0%和8.6%。

表2 谐振子优化参数对比Tab.2 Comparison of resonator optimization results

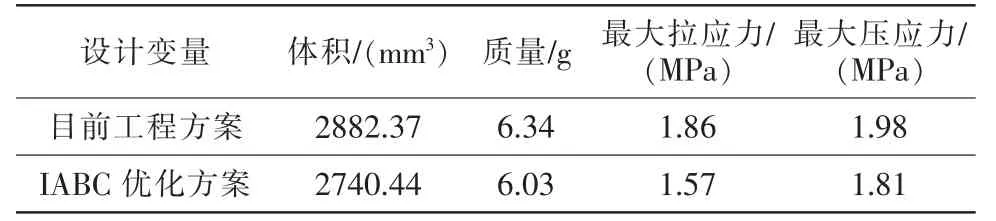
表3 谐振子优化结果对比Tab.3 Parameter comparison of resonator optimization

3.3 优化结果仿真校验

对表2 中IABC 算法优化方案进行仿真，应力仿真结果如图4 和图5 所示。

图4 IABC 优化方案拉应力仿真Fig.4 Tensile stress of IABC optimization scheme

图5 IABC 优化方案压应力仿真Fig.5 Compressive stress of IABC optimization scheme

从结果可以看出，经过IABC 算法优化后的谐振子最大拉伸应力及最大压缩应力分别1.565 Mpa和1.806 MPa。优化后方案各阶模态仿真结果如图6～图9 所示，振动频率如表4 所示。

图6 IABC 约束条件下二阶谐振模态Fig.6 Second modal simulation results of IABC optimization scheme

图7 IABC 约束条件下一阶弯曲模态Fig.7 First modal simulation results of IABC optimization scheme

图8 IABC 约束条件下轴挠性模态Fig.8 Flexible shaft modal simulation results of IABC optimization scheme

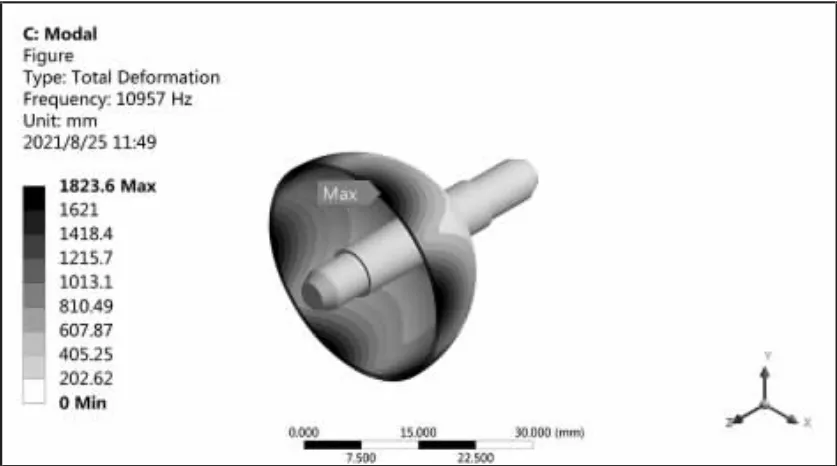
图9 IABC 约束条件下三阶弯曲模态Fig.9 Third modal simulation results of IABC optimization scheme

表4 结果表明，优化后谐振子满足相关约束条件，且二阶工作模态频率比一阶模态频率高出2106.5 Hz，可有效降低谐振子工作状态下的频率耦合影响，提高谐振子性能。

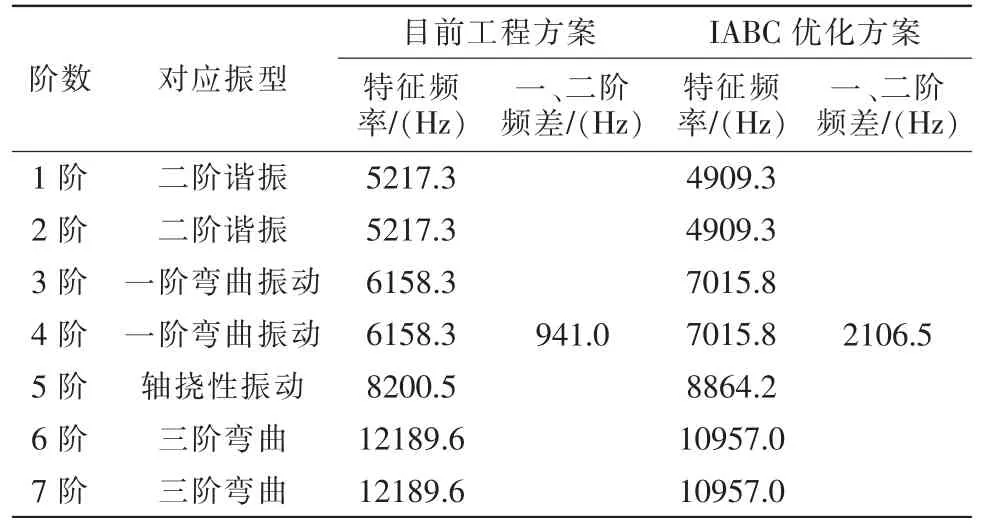
表4 两种谐振子方案各阶模态振动频率对比Tab.4 Comparison of vibration frequencies of different modes

4 结语

本文针对半球谐振陀螺谐振子多参数优化设计问题，通过建立谐振子带约束优化问题数学模型及采用惩罚函数方法，将谐振子优化问题转化为无约束最小化问题，并将改进人工蜂群智能算法应用于该多参数优化问题。最后将优化结果与现有工程应用方案进行仿真比较，对比结果表明，优化后谐振子在满足加工性要求和相关约束条件，优化目标函数减小了4.9%，同时有效降低干扰振动模态对于工作模态的影响。