高中数学数列试题的解题方法与技巧
2021-11-25陆钰
陆 钰
(江苏省泰州兴化市第一中学 225799)
数列是当下高中数学知识体系的重要组成部分,相应的题型复杂性及综合性比较强,对学生的数学解题能力具有较高要求.为了顺利地求解数列题,必须要结合实际的题型,灵活地选择恰当的解题方法与技巧,避免学生陷入解题困境.因此,在平时数列教学过程中,教师要注意将常用的一些数列问题解题技巧与方法传授给学生,力求可以有效提高他们求解数列问题的能力.
一、基于基本概念,求解数列问题
基本概念是数列学习的基础内容,也是最为关键的内容之一,会对学生求解数列问题产生比较大的影响.在初中数学学习过程中一般不会涉及到数列知识,所以学生是进入高中阶段之后首次接触数列问题.此时为了帮助他们更好地求解数列问题,必须要夯实他们的数学概念基础,指导他们在求解数列问题的过程中可以灵活地应用数列概念来解答问题.
例1现有等差数列{an},已知a4=4,S10=55,试求S4.
解析在本道数列题求解期间,可以结合等差数列的概念,灵活应用通项公式来求解问题,具体就是题目给定的条件代入等差数列的通项公式当中,求出a1和d.然后再套用前n项和公式来求解S4.
二、基于画图方法,求解数列问题
画图方法也是求解数列问题中比较多用的一种方法,主要是结合题干给定的已知条件开展绘图,之后根据直观的图象来找寻题干求解中所包含的数值之间关系以及内在规律等,这样可以轻松地对问题求解.
例2已知{an}为等差数列,am=n,an=m,且d≠0,m≠n,试求am+n=?
解析鉴于{an}为等差数列且d≠0,故可知an为关于n的一次函数,对应坐标(m+n,am+n)、(n,m)、(m,n)的3个点处在同一直线上.鉴于同一条直线的斜率相等可得:am+n=0.
三、基于数学性质,求解数列问题
在数列部分知识学习过程中,数学性质是非常重要的数学内容.而在求解某些数列问题过程中,如果可以灵活地应用这些相关数列的性质,那么可以显著提升数学问题的求解效率.因此,在数列部分知识学习过程中,可以有针对性地将数列性质方面的知识传授给学生,并使他们掌握如何利用性质来求解数列问题,这样也有利于锻炼及提升他们求解数列问题的能力.
例3{an}为等比数列,n为正整数,且a2a5=32,试求:a1a6+a3a4=?
解析在求解这道数列问题期间,如果直接采取常规的解题方法,按照等比数列的通项公式来求解问题,那么化简起来比较复杂,并且在求解问题中非常容易出错.而如果可以灵活地运用等比数列的性质,那么可以快速找到求解这道数列题的突破口,即:假定m+n=p+q保持成立,那么可得aman=apaq.
四、基于数学公式,求解数列问题
数学公式也是数列部分知识学习中需要学生掌握的重点内容,是求解某些数列问题中经常采用的一种解题方法,会对学生的解题能力发展产生极大影响.比如,数列的通项公式与前n项和公式等等,它们都是求解某些数列问题中必不可少的解题工具,对提升学生的解题能力大有帮助.
例4已知数列{an}的前n项和为Sn,满足6Sn=(an+1)(an+2),n∈N*,an>0,且S1>1,试求{an},通项公式.

五、基于函数思想,求解数列问题
函数思想是一种非常有价值的数学思想,在简化某些繁杂数学问题中常常会有神奇的效果.同理,在求解某些数列问题的过程中,也可以结合题干信息来灵活地应用函数思想简化问题求解过程,这样也可以锻炼学生思维的灵活性,对提高他们求解数列问题的能力有很大帮助.

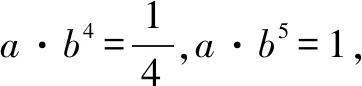
基于上述分析可知,该道数列题中有效地融入了函数方面的知识,所以在求解的过程中需要调用函数思想,但是要注意函数的基本性质,确保化简问题的每一步都要准确,全面.其中不合理的结果要及时排除,否则会对最终结果的准确性带来影响,造成错解.
六、基于方程思想,求解数列问题
同函数思想类似,方程思想也是高中阶段数学学习过程中需要学生重点掌握的一种数学思想.在求解某些数列问题的过程中,如果可以灵活地应用方程思想,也可以起到简化数学问题求解过程,提高解题准确率和效率的作用.所谓的方程思想,其在数列问题求解中应用时主要是依照一系列常用的数列公式来构建方程组,之后通过对方程组求解的方式来达到解决数学问题的目的.
例6已知{an}为等差数列,且S10=30,S15=195,试求S20.
解析针对这一道数列问题的求解,我们必须要搞清楚数列{an}的通项公式,但是由于题干条件中只给出了数列{an}的2个前n项和的结果,所以在实际的求解过程中可以借助方程思想来快速简化问题求解过程.
方法一假定{an}的前n项和Sn=tn+kn2,那么结合题干条件可得:10t+100k=30,15t+225k=195
通过联立二者,可以求得k=2,t=-17,所以可知:Sn=-17n+2n2
然后将n=20代入上式之后可以求得:S20=460.
方法二假定数列{an}的通项公式为an=a1+(n-1)d,那么结合题干条件可得:10a1+45d=30, 15a1+105d=195
通过联立二者,可以求得a1=-15 ,d=4,所以可知:

由此可见,在求解相关数列方面的数学问题时,如果可以灵活地运用方程思想,那么可以极大地简化数学问题求解过程,降低问题求解难度.但是在采用方程思想求解相应数列问题过程中要结合实际的求解目标灵活地设定求解方程,保证可以最大程度提高学生的解题能力.
总之,数列问题是高中数学教学中一类非常重要的题型,相应的求解方法众多,包括函数思想、方程思想、数学公式、数学概念、数学性质等等,它们都是求解数列问题中非常有用的方法.但是在实际的求解中,必须要对数学题干信息进行认真解读,在此基础上选择适宜的求解方法,保证可以最大程度提升学生求解数列问题的能力.
