化归思想在高中数学解题中的应用

杨 舒

(云南省怒江州民族中学 673100)

化归思想的解题思路主要是依据复杂问题所提出的有效解题方式，经过化归思想的运用，其不仅能够使学生面对复杂数学问题时，更好的理清思路，而且还能把复杂问题转变成一个或多个较为简单的问题，对其进行一一解决，并归纳到一起，最终实现问题解决的方法.目前，高中数学的解题教学当中，化归思想已经得到广泛运用，学生通过化归思想实施解题，就能更好的应对复杂、难度高的数学问题，从而使学生的数学成绩得到有效提升.

一、化归思想的形式

1.一般性与特殊性问题

化归思想作为常见的一种解题思路，其运用通常不能只局限在一种情境.通常而言，高中数学的解题中，较为常见的化归思想的运用情境中，最重要的就是一般性与特殊性问题.对于一般性与特殊性问题而言，其转换就是在面对复杂、特殊问题的时候，促进问题的简化，特别是面对短时间无法梳理出解答头绪的问题时，可将复杂、特殊的问题转变成一般可计算出的问题，以促使学生自身的解题思路更加清晰，并找出数学问题的具体解决方法.数学解题中，最为常见的应用场景就是计算多项式各项系数的和，在相关问题中，通常会出现多个未知数或者未知数高次幂等状况，若直接展开各项，并实施合并计算，计算量通常比较大，而运用化归思想，则能把当中的未知数设成常数1，将该值代入至全部计算中，以求取到相对简单的结果.经过该方式，就能使原先复杂化的计算过程实现简化，从而实现数学问题的有效解决.

2.分解和组合

分解和组合属于两个动作，在高中数学解题当中也是极其常见的.学生在解题中，最为常用到的就是分解.对于分解而言，主要就是把复杂问题进行细化，并通过不同的步骤实施逐一解决，通过该解题策略，就能使数学问题实施局部变更，在对整体的问题逻辑不受影响的状况下，实现部分解决.在所有的部分问题得以解决之后，将结果实施整合，即组合过程.

二、化归思想在高中数学解题中的应用策略

1.直接转化法

直接转化法作为数学解题中常见的解题法，运用于数学题的解答中，首先，需注重审视题目，将问题的条件作为出发点，合理的应用相关概念、公式、定理、法则等，经过有效沟通，实现推理、变形、计算之后，把原先的数学问题转变成相关基本问题，以获得相应的结论.将直接转化法运用于高中数学的解题中，一方面，数学教师在课堂教学当中，需注重基本定理、基本公式的深入讲解，其不仅需学生牢固记忆相关知识，而且还需清楚知识的来源，以促使学生积累到充足的知识，另一方面，教师需引导学生依据具体题目，注重直接转化法的运用，从而使学生充分体会到直接转化法的运用过程，并掌握其应用技巧.

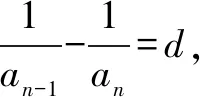
2.换元法

换元法主要指通过新变量的引入，把分式转化成整式，把高次转变成低次，以实现解题过程简化的解题方法.目前，换元法已经在不等式、方程、函数等相关试题中得到广泛应用.通常来说，换元主要包含三角换元、均值换元、局部换元等.想要使学生充分掌握换元法，需要对换元形式及其需注意的问题实施细致剖析，同时，数学教师可选择些经典题目，讲解换元法的具体运用方法，促使学生充分掌握换元法的运用技巧，从而使数学课程的解题正确率得到有效提高.将换元法运用于数学问题的解答中，其既能联系分散条件，呈现隐含条件，又能将条件与结论相联系，以实现快速与简化的获得结果的效果，从而使学生的解题能力得以提升的同时，深刻掌握数学思想的运用方法.

例如，已知x、y∈R，满足x2+2xy+4y2=6，那么z=x2+4y2的取值范围是____.

本题的题干相对比较简单，但是，学生如果不会运用化归思想进行换元，就无法有效解答本题，因此，教师需引导学生认真的观察题干，通过三角换元对该题实施解答.

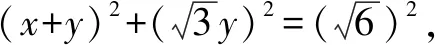
3.构造法

构造法主要指依据已学的相关知识与经验，对相应的数学模型进行构造，把问题转变成容易解决的数学问题.构造法的运用通常对学生自身的综合能力有着极高的要求，想要确保学生能够灵活的运用构造法，在课堂教学中，首先，需注重构造法的重点讲解，包含了一次函数、二次函数、构造向量等，以深化学生对构造法相关知识的理解，并充分掌握构造法的运用精髓.其次，数学教师需注重与数学习题相结合，引导学生通过构造法进行求解，并给予学生相应的指导，帮助学生学会通过构造法进行解题，从而使学生应用构造法的技巧与能力得到有效提高.

例如，已知等比数列{an}中，a1=2，a8=4，且函数f(x)=x(x-a1)(x-a2)……(x-a8)，f′(0)=( ).

A.26B.29C.212D.215

本题解法有着较强的技巧性，大部分学生在学习时，都会感到无从下手.因此，在课堂教学中，可指导学生对已知条件进行认真观察，引导学生通过构造法实施求解，而运用函数构造的方式f(x)=xg(x)之后，通过整体代换以及数列性质应用就能实现高效求解.设g(x)=(x-a1)(x-a2)…(x-a8)，那么f(x)=xg(x)，通过两边求导可得：f′(x)=g(x)+xg′(x)，因此，f′(0)=g(0)=a1·a2…·a8.又因为{an}是等比数列，a1=2，a8=4，所以，根据等比数列的性质可知，f′(0)=g(0)=a1·a2…·a8=(2×4)4=212.故本题的正确选项是C.

综上所述，高中数学的解题教学当中，化归思想的运用，不仅能实现学生自身解题思路的丰富，而且还能促使学生构建相应的知识体系.数学教师在具体教学时，既需要在理论知识的讲解中运用化归思想，又需通过具体例题运用化归思想，从而实现解题过程简化的同时，实现高中数学解题效率的提高.